寓数于形 以形解数
——谈“切线不等式”的应用
2022-11-24许荣好江苏省苏州工业园区星海实验中学215124
许荣好 (江苏省苏州工业园区星海实验中学 215124)
1 试题呈现
(1)若函数g(x)=f(x)-f′(x)存在极值,求m的取值范围;
(2)若函数h(x)=f′(ex)-f′(lnx),对任意的m∈R,若关于x的不等式h(x)≥m2+k2在(0,+∞)上恒成立,求正整数k的取值集合.
解析 (1)略.
(2)因为h(x)=(2e2x-2mex+m2)+(2ln2x-2mlnx+m2),所以对任意m∈R,(2e2x-2mex+m2)+(2ln2x-2mlnx+m2)≥m2+k2在(0,+∞)上恒成立,即对任意m∈R,m2-2(ex+lnx)m+(2e2x+2ln2x-k2)≥0在(0, +∞)上恒成立,故Δ=4(ex+lnx)2-4(2e2x+ 2ln2x-k2)≤0在(0,+∞)上恒成立,即k2≤(ex-lnx)2在(0,+∞)上恒成立.
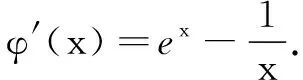
上述解答关键是处理k2≤(ex-lnx)2在(0, +∞)上的恒成立问题,难点在于φ(x)=ex-lnx的最小值难以直接通过一次求导直接给出,只能借助于二次求导以及函数零点的相关知识加以解决.一般学生在处理此类问题时,无法像答案这样完美无缺,考虑周全.学生们迫切地需要一种简单快速且有效的方法.因此我们可以借助于“切线不等式”来加以解决.
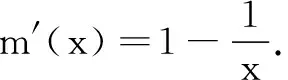
2 “切线不等式”的概念
切线不等式来源于函数f(x)的几何图象,通过观察f(x)的图象总是在切线y=ax+b的上方(或下方),从而得到切线不等式f(x)≥ax+b(或f(x)≤ax+b).在平时的高中数学教学中,常见的切线不等式如图1所示.
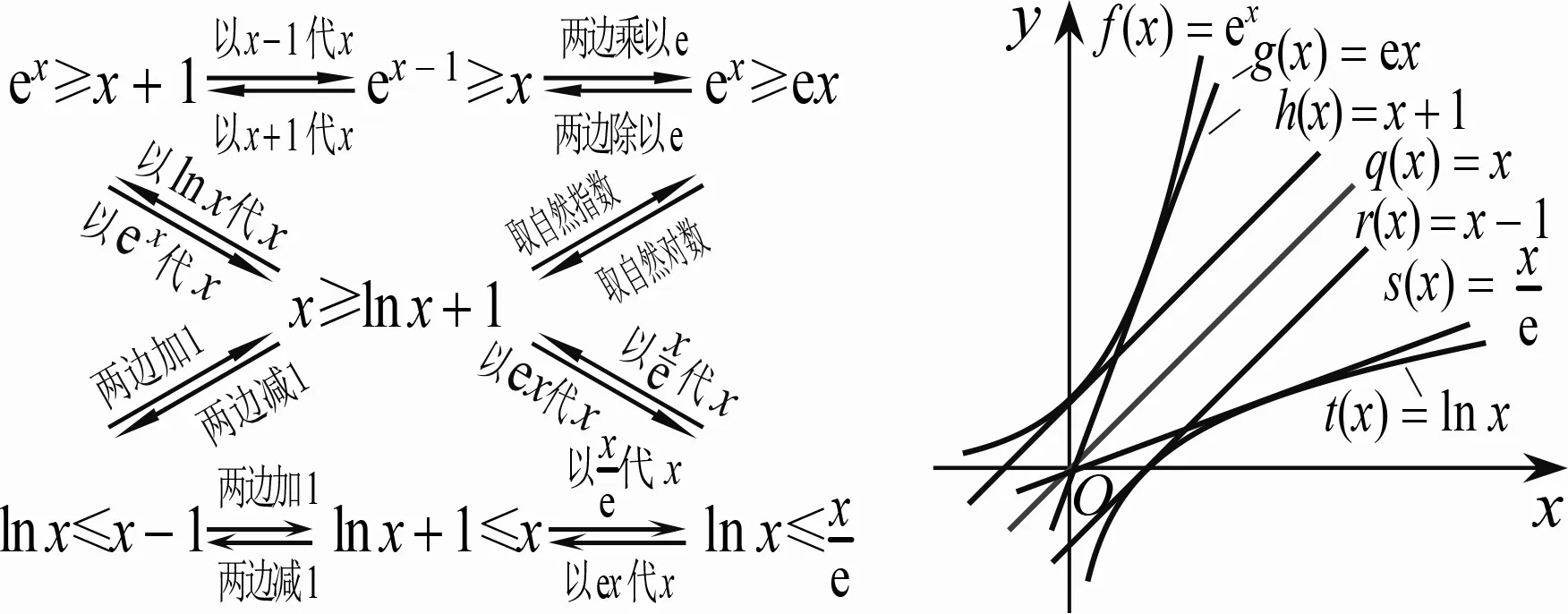
图1
无论是浑然天成的代数结构,还是优美对称的几何直观,都让人赏心悦目、拍案叫绝.
3 “切线不等式”的应用
当我们熟悉切线不等式之间的关系及其变形形式后,自然要看看它们在解题实践中的应用.
3.1 与函数相关的不等式问题
例1(2020山东二模)已知函数f(x)=ex-x2.
(1)求曲线f(x)在x=1处的切线方程;
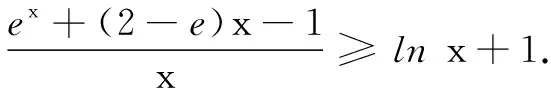
解析 (1)略.
(2)这个不等式的常规证明较为麻烦,观察不等式的右边,发现很像切线不等式的变形,因此采用切线不等式解决此题.
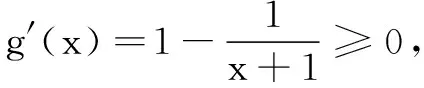
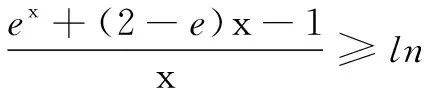
反思回想我们的解题过程,若是不借助切线不等式的变形,此题需要学生进行大量的构造,通过尝试导数去求解最值进而证明不等式,过程较为繁琐,操作起来较为困难;相反,若是借助切线不等式,只需要进行简单的放缩,通过移项和常规求导即可解决,优势明显.
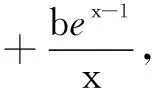
(1)求a,b的值;(2)证明:f(x)>1.
解析 (1)略.
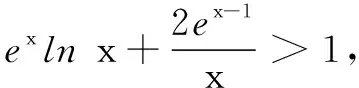
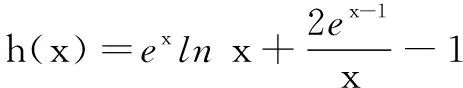
3.2 形如的不等式问题
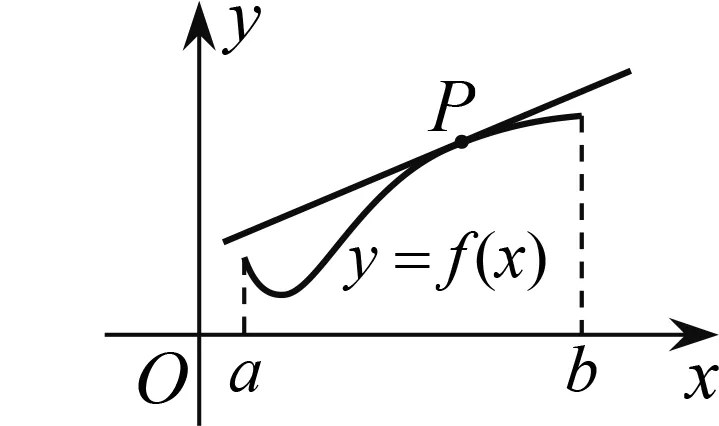
图2
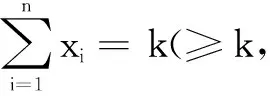
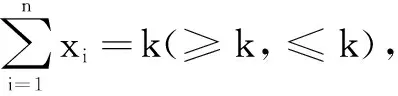
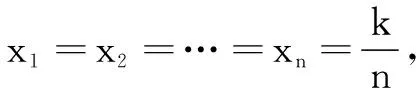
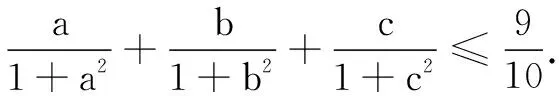
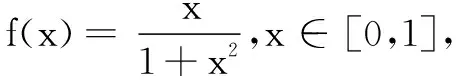
反思由于观察到函数图象是上凸的,利用原函数图象和切线的位置关系,采用数形结合的方法对原不等式进行放缩,最后由不等式的性质,三个式子相加,证得原命题.此方法既培养了学生对数形结合思想的理解,也减少了复杂的含字母运算.
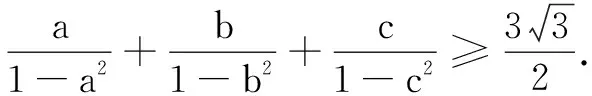
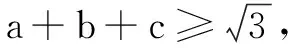
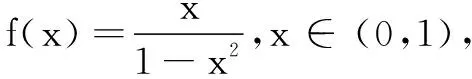
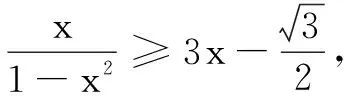
反思运用“切线不等式”法证明不等式时,需注意已知条件是单变元的和式,特征不等式左边也是和式,当发现已知条件或特征不等式不符合上述条件时,需要通过适当的转化后再使用“切线不等式”.
4 反思与展望
虽然高中的试题一直在继承中创新,但也不回避已经考过的类似试题.此类数学题集中了命题人的智慧,是经过反复打磨的精品,因此在备战高考时,通过研究各省市的历年真题,把握高考试题的方向和命题规律,精做题、做精题,这样才能走出题海,提高效率.不等问题在高考中一直扮演着重要地位,综合性强,区分度高,是数学学科核心素养高低的分水岭.在研究函数的过程中,若能利用好“切线不等式”这一有力工具,往往就能出奇制胜,此法对比常规方法而言具有巨大的优越性和间接性.遗憾的是,“切线不等式”这样的称呼,教材中并没有明确给出,至今仍是一个“民间”说法,因此在应用时还需要给出适当的证明,这不免增加了解题的长度.教师在日常教学中,为了提升学生的数学核心素养、提高学生的数学思维品质,应在恰当的时候有针对性地讲授一下,以便拓宽学生的解题视野.
