大型飞机机翼典型盒段后屈曲分析与验证
2022-11-24王鹏飞金三强
王鹏飞,金三强
(中国特种飞行器研究所 试验与计量中心,湖北 荆门 448035)
机翼盒段一般由加筋壁板、前后梁、翼肋等结构组成,是机翼主要承力部件。机翼盒段的设计对机翼的承载性能甚至对整个飞机都有着至关重要的作用。机翼典型盒段受纯弯曲载荷时,上壁板承受压载荷。一般为了优化翼盒重量,在极限载荷情况下(或小于极限载荷)上壁板结构允许进入屈曲状态。进入屈曲状态后,上壁板上的一部分载荷会重新分配到加强筋上,加筋壁板的承载能力往往大于其临界屈曲载荷。
机翼典型盒段上的蒙皮为筋板结构,目前对于机翼盒段的强度设计主要集中在加筋壁板的稳定性方面[1]。余明等[2]使用准静态法对飞机机翼盒段结构失稳破坏形式和极限承载能力进行了预测分析。林国伟等[3]采用五种不同的失效准则对L型加筋结构进行了分析并结合试验验证,为复合材料加筋壁板后屈曲分析提供参考。王彬文等[4]采用Kriging模型构建了能够表征后屈曲特性的代理模型,并采用蒙特卡罗随机模拟的方法获得了加筋壁板后屈曲载荷概率分布。刘存等[5]考虑材料和几何双重非线性对舰载机壁板剪切后屈曲承载能力进行了预测与试验验证。张国凡等[6]使用渐进式损伤方法预测了复合材料整体化多墙盒段后屈曲承载能力并进行了试验验证。万春华等[7]考虑材料和几何非线性,对机翼盒段加筋结构后屈曲有限元建模方法进行了研究。韩庆等[8]针对复合材料层合加筋结构的后屈曲问题,采用FORTRAN编程,对不同机翼盒段进行了后屈曲计算和分析。薛斌[9]利用有限元法对不同结构形式的典型盒段承压结构进行了设计与分析。
机翼盒段各组成结构互为支持,仅分析上壁板加筋板结构的稳定性,无法涵盖机翼盒段的稳定性分析问题。本文以大型飞机机翼典型盒段为研究对象,考虑材料非线性和几何缺陷,利用ABAQUS有限元分析软件中Riks弧长法进行了后屈曲仿真分析,预测了机翼典型盒段的破坏模式和承载能力,并与破坏试验进行了对比验证,为机翼盒段结构稳定性优化设计提供参考。
1 机翼典型盒段屈曲特征值分析
1.1 机翼典型盒段构型
机翼典型盒段结构形式如图1所示,其总体尺寸为长1 960 mm、宽1 380 mm、高625 mm,主要由上下“工”字型加筋壁板、前后梁、4个翼肋组成。本文以典型盒段上壁板为研究对象,蒙皮厚度为4.57 mm,长桁高度为53.50 mm,长桁腹板厚度为3.94 mm,长桁间距为165.00 mm。
1.2 机翼典型盒段建模
在气动载荷的作用下,机翼典型盒段主要承受弯矩、扭矩和剪力载荷。根据机翼典型盒段结构的传力特点以及飞机实际结构形式,在机翼典型盒段两端各延伸一段分别作为加载段和支持段。
机翼典型盒段的上下蒙皮、前后梁、中间肋等结构均采用壳单元(shell单元)模拟,铆钉连接采用广义弹簧单元(bush单元)模拟,加载段和支持段的上下蒙皮和前后梁等结构采用壳单元(shell单元)模拟。加载段、支持段与机翼典型盒段采用共节点的方式连接,如图2所示。在支持段端部节点处施加固支约束,在加载段端部节点建立MPC,在x轴方向施加2 107 kN·m的弯矩。
典型盒段的结构材料为铝合金,材料牌号及参数如表1所示。

表1 机翼典型盒段结构材料牌号及参数
1.3 机翼典型盒段屈曲特征值
根据前述所建机翼典型盒段模型,对其进行线性屈曲分析,得到机翼典型盒段前4阶特征值分别为:0.697 4、0.703 4、0.775 6和0.788 9,前4阶的屈曲模态如图3所示。
各阶特征值间隔较小,表明屈曲临界载荷对初始缺陷较为敏感,对典型盒段有必要进行缺陷几何的非线性屈曲分析。
2 机翼典型盒段后屈曲分析
2.1 引入初始缺陷
由于机翼典型盒段在弯矩的作用下,上壁板承受压力载荷。在载荷的作用下机翼典型盒段有可能在初始屈曲后进入后屈曲状态。为此,将其前2阶屈曲模态乘以0.01的权因子引入后续的计算模型。初始缺陷格式为:
式中:κj为指定模态的加权因子;φj为第j阶模态形状;m为引入模态阶数。
2.2 机翼典型盒段后屈曲分析
引入初始缺陷后,对机翼典型盒段进行后屈曲分析,所得加载点的载荷-位移曲线如图4所示。由图4可见,施加载荷的初始阶段加载点处的载荷-位移曲线呈良好的线性关系。当载荷施加到1 475 kN·m时(图4,bucking point),机翼典型盒段出现初始屈曲,进入了后屈曲状态。随载荷的继续增加,当载荷为2 033 kN·m时(图4,failure point),曲线达到顶点后整体结构迅速失去承载能力。由此可知,机翼典型盒段的承载能力大于其初始屈曲载荷值。
机翼典型盒段后屈曲分析的应力及变形结果如图5所示。由图5(a)可见,当载荷为1 475 kN·m,即盒段上壁板中间考核段发生屈曲时,较大载荷分布在考核段中心点及其周边的空心矩形区域。由图5(b)可见,当载荷为2 033 kN·m时(机翼典型盒段承受的最大载荷),较大载荷在上壁板中间的呈网状分布。结合图4和图5(c)可见,在最大载荷条件下,随着位移的增大(变形量的增加),机翼典型盒段上壁板结构出现折皱,导致整体结构失去承载能力。此时,最大载荷主要集中在机翼典型盒段上壁板的折皱处。
3 机翼典型盒段破坏试验验证
3.1 机翼典型盒段破坏试验
机翼典型盒段破坏试验在试验加载装置上进行。机翼典型盒段在该装置上可分为与支持夹具相连的过渡段、考核段(试验段)和与加载夹具相连的过渡段。机翼典型盒段通过支持段夹具以悬臂式的形式固定在试验台架上。在试验加载装置加载段布置4个作动缸,靠近机翼典型盒段考核段的2个作动缸(左侧2个)施加拉向载荷,另外2个作动缸(右侧2个)施加压向载荷。通过4个加载点的载荷组合,对试验件施加2 107 kN·m的纯弯矩载荷。
为研究机翼典型盒段在弯曲载荷下的屈曲情况,在盒段考核段上壁板A、B、C、D截面上同一位置正反两面对称粘贴应变片,应变片粘贴位置如图6所示。根据盒段上壁板同一位置正反两面对称的应变片随载荷施加的变化情况,判断机翼典型盒段是否发生屈曲。图7所示为机翼典型盒段上壁板试验所得不同截面的载荷-应变曲线,图中图例表明应变片在图6中所处的位置。由图7可见:施加载荷的初始阶段,载荷-应变曲线呈良好的线性关系;当加载到约为1 460 kN·m时,A、B、C、D截面上的载荷-应变曲线均出现分叉,表明机翼典型盒段上壁板发生局部屈曲;随着载荷的继续增加,约为1 970 kN·m时,载荷-应变曲线出现极大值。此时,机翼典型盒段上壁板中间考核段出现大面积折皱,两侧前后梁对应位置折坏,如图8所示。
3.2 后屈曲分析与试验结果对比
为验证前述有限元方法分析的有效性和准确性,对机翼典型盒段的有限元分析结果与破坏试验的试验结果进行对比,结果示于表2。由表2可知:机翼典型盒段后屈曲分析得到的失稳载荷及破坏载荷与试验结果误差均小于5%;机翼典型盒段后屈曲仿真分析预测的破坏模式与试验结果相似:机翼典型盒段上壁板考核段内失稳形成折皱,导致典型盒段整体结构失去承载能力。
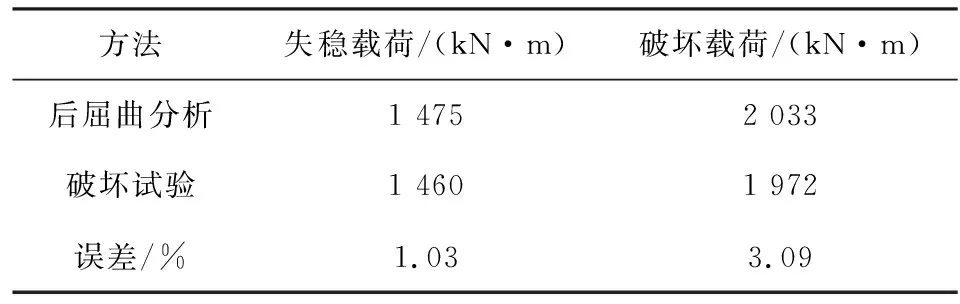
表2 有限元分析结果与试验结果对比
4 结论
考虑材料非线性和几何缺陷,利用ABAQUS有限元分析软件中Riks弧长法对机翼典型盒段进行了后屈曲仿真分析,并与破坏试验结果对比,可得出以下结论:
(1)通过机翼典型盒段屈曲特征值分析,前4阶特征值间隔较小,表明有必要对机翼盒段结构进行缺陷几何的后屈曲分析;
(2)有限元分析结果表明,机翼典型盒段的承载能力大于其初始屈曲载荷值;
(3)通过机翼典型盒段后屈曲分析得到的其失稳载荷和破坏载荷与试验误差均在5%以内,预测破坏模式与试验结果相似,可为机翼典型盒段稳定性优化设计提供参考。
