基于MATLAB的随机性数学思维培养的探索与实践

张清叶 尚邵阳

(1.河南工学院理学部;2.河南工学院非线性优化算法研究所 河南新乡 453003)

中国科学院数学与系统科学研究院周川认为，数学的本质在于数学思维。数学思维是指在思考和解决问题的过程中，对数学思想、方法的合理运用能力，数学思维不仅是一种知识，还是一种能力[1-2]。前贵州大学校长陈叔平认为，数学是一套独特的语言体系和思维方式，它让人变得更明白一些，让脑子更好使，条理更清晰，逻辑严谨，表述准确、简洁，不妄下结论，不随意批评，不去骗人，也不受骗。事实上，数学不仅是自然科学的基础，也是重大技术创新的基础，历史上的科技创新无不与数学有关，其早已成为航空航天、国防安全、信息、能源、海洋等领域不可或缺的重要支撑。现在的人工智能，更是离不开大数据和数理统计。

作为高校本科阶段三大公共数学课之一的《概率论与数理统计》是唯一一门研究随机性的课程[3]，其研究内容是我们日常生活中最常见、最有用的，影响了我们的认识论、方法论，甚至颠覆了我们的世界观。从20世纪电子信息技术的迅速发展，到21世纪大数据时代的到来，几乎所有的科学技术领域、工农业生产领域以及国民经济的各个部门都有其理论和方法的应用，小到掷骰子、分赌本，大到地震预报、人口预测、火箭卫星的发射等。然而，在传统教学中，受课时及课程定位的影响，概率论训练的多是一些组合技巧，数理统计讲的是一些标准方法。在题海和脑力游戏中，往往会让学生学得很苦，感觉抽象、难学、无用，严重偏离了这门课程培养学生随机性数学思维的初衷，不利于创新人才的培养。在此现实背景下，如何深刻理解概率论与数理统计的思想，进而培养学生的随机性数学思维[4-5]是亟待解决的问题。

众所周知，对随机现象的研究是通过随机试验进行的，如著名的蒲丰投针试验、高尔顿钉板试验等。在传统教学中融入数学实验[6]，让学生在折腾中去体验数学的发现过程，在真实情景中感受知识的落地，势必会激起他们的好奇心和创新意识，对培养其随机性数学思维能力将会是一条行之有效的途径。MATLAB是美国MathWorks 公司于20 世纪80 年代推出的一套以矩阵为基础的高性能数值分析和计算软件[7]，其将矩阵运算、数值分析、图像处理、编程技术等结合在一起，为用户提供了强有力的分析计算和程序设计工具，尤其是其可视化功能和各种工具箱受到绝大多数科技工作者的青睐。笔者在概率论与数理统计课程的教学过程中，利用对随机现象研究的本原方法，即随机试验来研究概率进而解决问题，其中随机试验在MATLAB 平台完成。这一做法极大地调动了学生学习的积极性，收到了很好的教学效果。下面分享笔者在教学中基于MATLAB的几个案例，期待能够抛砖引玉。

1 投硬币实验

问题：抛掷一枚均匀的硬币，正面向上的概率为0.5。

实验目的：验证随机事件的概率。

实验设计：抛掷一枚均匀的硬币，令Xi=1表示第i次抛得正面，Xi=0表示第i次抛得反面，则Xi服从两点分布。由伯努利大数定律，伯努利试验中随机事件的频率依概率收敛于其概率，可利用频率来估计概率。将硬币连续抛掷n次，若正面向上累计出现了k次，则频率

MATLAB代码：

反思与提高：

概率是事件本身的固有属性，具有确切的数值。而频率则与试验次数和某次试验的结果有关，具有不确定性。但频率会随着试验次数的增多依概率收敛到事件的概率。为此，可通过增加试验次数，一方面求概率更为准确的数值，另一方面验证频率的稳定性。改进后的MATLAB代码如下：

运行此代码后，返回，具体情况见图1。不难发现，随着试验次数的增加，频率逐渐稳定到事件“正面向上”的概率0.5。

图1 抛硬币实验频率的稳定性验证

2 圆周率π的估算

问题：利用几何概型估算圆周率π。

实验目的：利用蒙特卡洛法计算圆周率。

实验设计：在第一象限内画单位正方形，即画以坐标原点为左下角顶点、边长为1的正方形，并以坐标原点为圆心，画1/4单位圆周，具体见图2，则

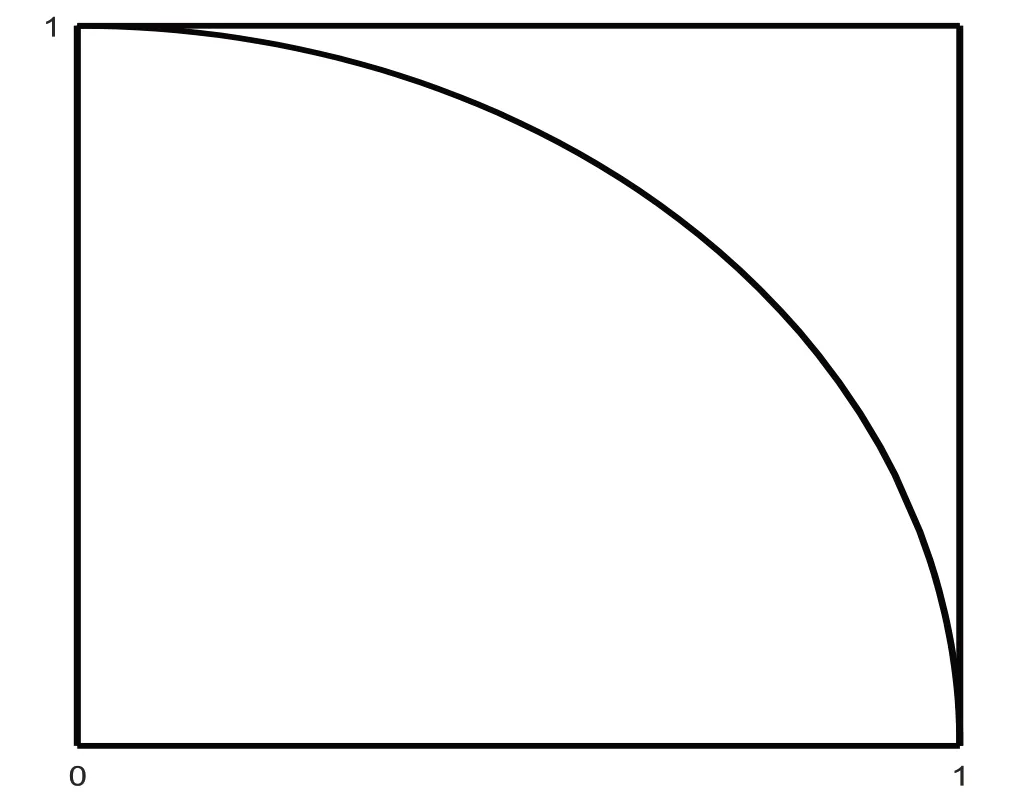
图2 估算圆周率实验设计

根据几何概型，若在图1所示的图形上铺满芝麻，则落入1/4 圆内的芝麻粒数与落入正方形内的芝麻粒数之比应为π/4。意到这一事实，可在Matlab平台上这样设计实验：在单位正方形内随机投点，记所投点的总数为n，落入1/4 圆内的点的个数为k，则，从

MATLAB代码：

3 三门问题

问题：三门问题（Monty Hall problem）亦称为蒙提霍尔问题或蒙提霍尔悖论[8]，出自美国的电视游戏节目Let′s Make a Deal。节目进行到某个环节，参赛者会看见三扇关闭了的门，其中一扇门的后面藏有一辆汽车，另外两扇门的后面各藏有一只山羊。当参赛者选定了一扇门，但未去开启的时候，节目主持人开启剩下两扇门的其中一扇，露出一只山羊。紧接着主持人会问参赛者要不要换另一扇仍然关着的门，即换另一扇门是否会增加参赛者赢得汽车的概率。

实验目的：通过理性推理(计算概率)验证直觉判断是否可信。

实验设计：此问题可以利用概率论的知识，通过设出事件，根据贝叶斯公式进行求解。这里介绍基于MATLAB 平台，利用模拟的方法分别计算换门和不换门赢得汽车的频率。注意到参赛者不知道车在哪扇门的后面，而节目主持人事先知道，并且主持人总是在剩下的两扇门中打开后面藏有山羊的门。设共做了n=1000 次实验，a、b分别为换门和不换门赢得汽车的次数，实验前a=0，b=0。每次实验开始时，车等可能的藏在每一扇门的后面且参赛者随机的从三扇门中选择其中一扇。若参赛者选中后面藏有汽车的门，则不换门可赢得汽，此时b增加1；若参赛者选择的门后面没有汽车，则换门可赢得汽车，此时a增加1。a/n，b/n分别为n次实验换门和不换门赢得汽车的频率。

MATLAB代码：

运行代码后，可得进行1 000 次实验时，参赛者换门和不换门赢得汽车的频率。若想求得概率，可通过增加每组实验的实验次数，如n=10 000,100 000等，并多做几组实验（可通过for循环实现），然后取每组实验所得频率的平均值来估计概率。

结果发现，换门赢得汽车的频率是不换门赢得汽车频率的2倍，即换门可增加赢得汽车的概率，参赛者应选择换门，这与人们的直觉不太一致。

4 投资组合问题

随着近年来我国资本市场的发展和证券交易规模的不断扩大，越来越多的资金投资于证券市场，与此同时市场价格的波动也十分剧烈，如何选股并确定投资组合方案使得投资收益大且风险小一直是金融领域的热门话题。由于股票价格具有随机性，可看成服从随机游走，从而处理这个问题不能直接用确定性的方法。以2020年第三届中青杯全国大学生数学建模竞赛的B题为例[9]，确定对附件给出的10支股票如何进行投资。

实验目的：确定投资组合方案。

实验设计：首先对附件给出的数据进行处理，若某只股票某天交易数据缺失，则将其他股票当天交易数据一并删除。利用10 只股票的日收盘价采用算术平均计算其日收益率Rit,即第i只股票第t天的日收益率为Rit，令ri=E(Rit)表示第i只股票的平均收益率，Σ=(σij)10×10表示10只股票的协方差矩阵，其中σij=cov(ri，rj)，则根据马科维茨投资组合理论，用投资组合的平均收益率来衡量收益，用投资组合的方差来衡量风险。设10 只股票的投资比例为xi(i=1，2，…，10)，则可得确定最优投资组合方案的均值方差模型如下。

其中，r0为预期收益的阈值，即投资者期望获得的最小收益，通常要大于无风险利率。上述MV 模型为一个二次规划问题，可以利用MATLAB 的quadprog 函数进行求解。

MATLAB代码：

运行代码后，可得到对应于不同收益率阈值的投资组合方案及相应的风险水平（均方差）。投资者可根据自己的投资偏好和风险承受能力来选择相应的投资组合方案。

5 结语

大数据时代的到来，随机性数学思维显得比以往任何时候都更加重要，如何对繁杂、海量数据进行探索，找出其背后蕴含的规律是时代赋予我们的使命。作为高校在读大学生，掌握随机性数学思维的方法尤其重要。而概率论与数理统计课程作为唯一一门在大学期间研究随机性的数学学科，教师应不断改进教学模式，使之成为一门学生感兴趣的、有用的学科。信息技术的发展，无疑给概率论与数理统计的实验教学提供了极大便利。教师应让学生在实验中发现规律，在折腾中解决问题，逐步培养其随机性数学思维能力、创造性解决问题的综合能力和实践能力。