基于注意力机制的CNN-LSTM模型股价趋势预测

2022-11-23刘天阳

科技资讯 2022年23期

刘天阳

(上海对外经贸大学金融管理学院上海 201600)

股价预测一直是量化投资领域关注的重点问题，人们试图通过分析与股价相关的历史数据得出股价的变化规律，进而获得超额收益。

常用的预测模型可分为线性预测模型与非线性预测模型，由于股价通常会受到多种多样的因素共同影响，线性预测模型一般很难有效地预测股价。近年来，机器学习与深度学习方法中许多非线性预测模型被应用到量化投资领域，且较线性预测模型具有更强的预测性能，李斌等人通过对比机器学习模型与线性回归模型，发现在我国A股市场中，机器学习模型的预测性能优于线性回归模型，在机器学习模型中，非线性机器学习模型预测性能优于线性机器学习模型，深度学习模型表现最优[1]。Leippold 等人也发现，对于我国A 股市场，非线性机器学习模型的预测性能优于线性回归模型，深度学习模型预测性能最优[2]。考虑到深度学习模型较机器学习模型与线性回归模型具有特征工程成本低、预测性能强等特点，该文将使用深度学习方法对我国沪深300指数成分股价格进行预测。

在深度学习模型中，黄婷婷与余磊使用抗噪自编码器（DAE）与LSTM的复合模型，对恒生指数价格进行预测，较传统的神经网络模型具有更高的预测精度[3]。耿晶晶等人使用CNN 与LSTM 的复合模型，对我国股指价格进行预测，发现CNN-LSTM 模型较单一模型来说具有更强的预测性能[4]。孙存浩等人使用前馈神经网络（FNN）与LSTM的复合模型，对上证综指价格进行预测，发现FNN-LSTM 模型的泛化能力较传统机器学习模型与LSTM 模型更优[5]。胡聿文使用主成分分析（PCA）与LSTM 的复合模型，对平安银行价格进行预测，发现PCA-LSTM模型泛化能力优于单独使用LSTM模型[6]。

基于上述研究可以发现，学者们更偏好使用复合模型对价格进行预测，但是，上述复合模型均无法分辨时间维度信息的重要性水平。为了进一步提升模型预测能力，该文将基于CNN-LSTM 模型架构，将注意力机制引入LSTM 端，提出了一种基于注意力机制的CNN-LSTM模型，利用变分编码器（VAE）产生的特征，对比引入注意力机制前后的CNN-LSTM、CNN与LSTM这4 种预测模型对我国沪深300 成分股价格趋势的预测性能，并构建有效的投资组合。

1 理论基础与模型构建

该文使用VAE模型完成特征工程，基于注意力机制的CNN-LSTM 模型主要由FNN、CNN 与LSTM 部分构成，模型架构如图1 所示，首先，时间序列数据由CNN 部分提取空间维度特征，而后输入引入注意力机制的LSTM 部分提取时间维度特征，最后经FNN 部分输出。该模型与未引入注意力机制的CNN-LSTM 模型参数设定跟单独使用CNN模型与LSTM模型保持一致，4种预测模型均设定100轮（epochs）迭代，损失函数为交叉熵（Cross Entropy），结合适应性矩估计（Adam）优化器训练模型，4 种预测模型的调参策略将在第三部分第三小节中介绍，其他细节将在下述小节介绍。

图1 基于注意力机制的CNN-LSTM模型架构

1.1 FNN（Feed-forward Neural Network）

FNN 模型主要由输入层、隐藏层与输出层3 个部分组成，其中，隐藏层深度不固定，整体网络依靠节点联系起来，每一个节点称为“神经元”，输入数据经线性变换后，由非线性的激活函数输出，输出结果作为下一层的输入，直至最后输出得到正向传播计算结果，而后根据损失函数计算误差，通过链式求导计算系数梯度，使用梯度下降算法修正系数，不断循环这个过程，最终完成模型训练。常用的激活函数有Sigmoid、ReLu（Rectified Linear Unit）等，常用的损失函数有Cross Entropy、均方误差（MSE）等。

在该文中，FNN 模型用于各个预测模型的输出部分与VAE 模型的设计中，具体细节将在下述小节介绍。

1.2 VAE（Variational Auto-Encoder）

VAE 模型为一种生成模型，主要由编码器与解码器组成，编码器计算输入数据在隐空间的均值与方差，通过隐空间的概率分布生成数据，而后由解码器重构这些数据。VAE模型的损失函数由重构损失（Recon‐struction Loss）与KL（Kullback-Leibler Loss）散度决定，重构损失负责度量重构数据与原始数据的相似程度，KL 散度负责度量一般正态分布与标准正态分布的差异。

在该文中，重构损失用MSE 度量，VAE 整体损失公式为

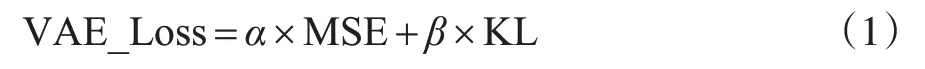
编码器与解码器均基于FNN网络构成，结构如图2、图3所示。

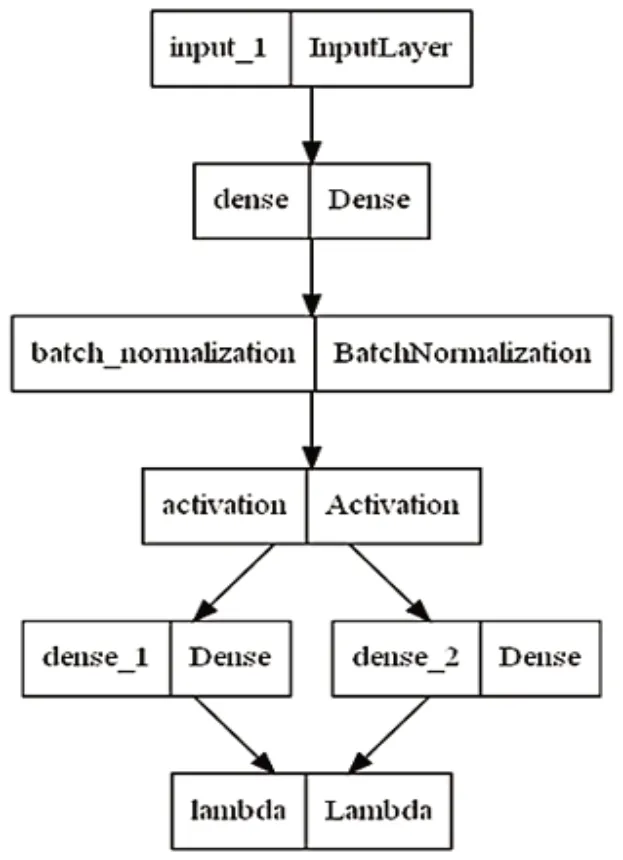
图2 VAE编码器结构

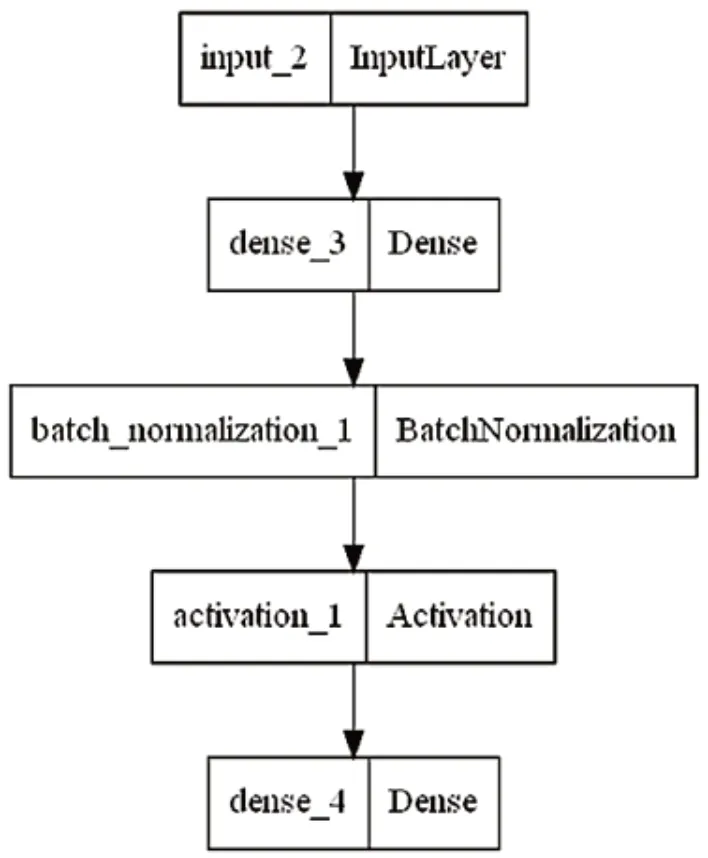
图3 VAE解码器结构

其中，input_1 层与dense_4 层特征输入输出数目均为6，dense 层与dense_3 层神经元个数设定为8，dense_1与dense_2负责计算数据在隐空间的均值与方差，隐空间概率分布函数为标准正态分布，神经元个数调参范围为4～16，lambda 层用于生成数据，设定损失函数为（1）式，α与β值均为0.5，设定100轮（epochs）迭代，结合Adam优化器训练VAE模型，激活函数均使用ReLu，最终通过计算最后5epochs 最小损失均值确定dense_1与dense_2的神经元个数。

1.3 CNN（Convolutional Neural Network）

CNN模型主要由卷积部分、池化部分与FNN部分构成，卷积部分通过卷积核来搜集空间特征，一般可以通过设置多个卷积核更加充分地提取特征，而后池化部分对卷积部分提取的特征进行浓缩，得到相对较为重要的特征，最终展平这些特征并输入FNN部分中得到计算结果。

在该文中，CNN 模型架构使用了图1 中CNN 与FNN部分架构，Input_2层输入数据结构宽度为6，高度为42，颜色通道为1，conv2d 层卷积核大小为3×3，输出通道数目范围设为（4，8，16，32，64），max_pooling2d层池化大小为2×2，dense_1 层神经元个数为8，激活函数均为ReLu，dense_2 层神经元个数为2，激活函数为Sigmoid。

1.4 LSTM（Long Short Term Mermory network）

LSTM模型是循环神经网络（RNN）的一种，由于传统RNN网络参数共享的设计，使得传统RNN在处理长时间序列数据时会产生梯度消失或梯度爆炸等问题，LSTM模型通过门控制结构与记忆状态的设计，在一定程度上缓解了这些问题。LSTM 模型的控制门由遗忘门、输入门与输出门构成，遗忘门负责减少记忆量，输入门负责更新记忆状态，输出门负责输出当前状态的计算结果。

该文的LSTM 模型使用了图1 中LSTM 与FNN 部分架构，Input_2 层输入数据结构时间步长为42，维度为6，lstm层神经元个数范围设为（5，25，50，100），激活函数为ReLu，FNN 部分架构与CNN 模型中的FNN 部分架构保持一致。

1.5 注意力机制

如图1中注意力机制部分所示，该文将LSTM每一步的输出矩阵H输入一层FNN，经Softmax函数计算得到每一步输出的权重矩阵W，最后将矩阵H 与矩阵W相乘完成注意力的引入。

2 实验及分析

2.1 实验环境

该文的实验环境为Windows 11 64位操作系统，基于Python 3.8.4环境编程，所有模型构建与训练均基于Tensorflow-GPU2.8.0版本。硬件配置为CPU Intel Core i5-10200H，内存为16 GB，显卡NVIDIA GeForce RTX 2060。

2.2 数据简介

该文选取了2021年1月1日至12月31日沪深300指数成分股k 线数据，数据频率为5 min，数据来源于Baostock 平台。该文将数据集划分为3 个不相交的时间段，以2021年1月1日至5月31日的数据为训练集，并根据训练集可观测到的沪深300指数成分股更新股票池，并剔除了这期间存在停牌的股票，2021 年6 月1日至6月31日的数据为验证集，2021年7月1日至7月31日的数据为测试集，完成第一轮各个模型的训练与预测，按月重新计算各个模型，不断滚动6 轮，预测至2021 年12 月31 日。以第一轮中各个模型用到的原始数据集为例，数据描述性统计如表1所示。

表1 沪深300指数成分股k线数据描述性统计

VAE模型处理后的训练集数据描述性统计如表2所示。

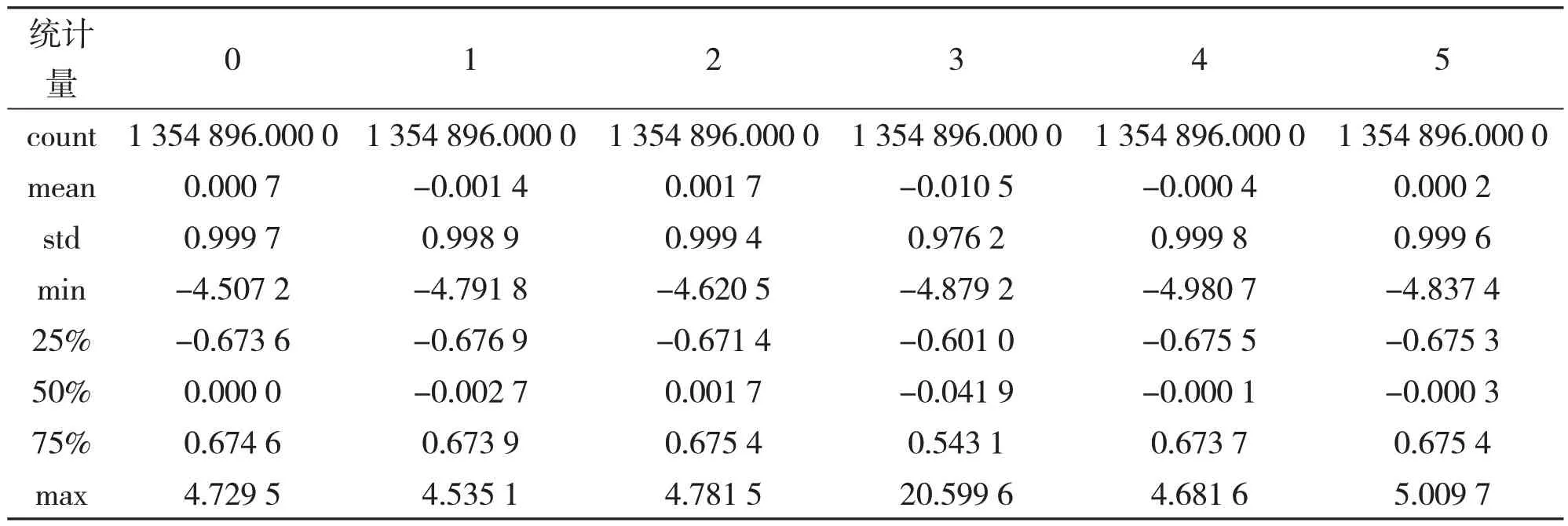
表2 训练集数据描述性统计

2.3 投资策略与调参策略

该文的投资策略为：在每个交易日的14∶30 进行交易，并于下一个交易日的14∶30调仓换股，设定交易手续费为2.5‰，4 种预测模型的输入数据结构均为42×VAE隐空间维度的二维数组，若股价上涨幅度大于交易手续费，标签记为1，否则记为0，输出为2 分类的概率值，每个交易日选取预测上涨概率最高的5 支股票构成投资组合。

该文的调参策略为：根据4 种预测模型在验证集上的投资组合收益来确定参数，保存其在验证集累计收益率最高时的参数，为了保守起见，该文对每一个待调参数均进行了10次重复实验。

2.4 结果分析

6 轮实验结果的整体情况见表3。各个预测模型在测试集的累计收益率曲线见图4。

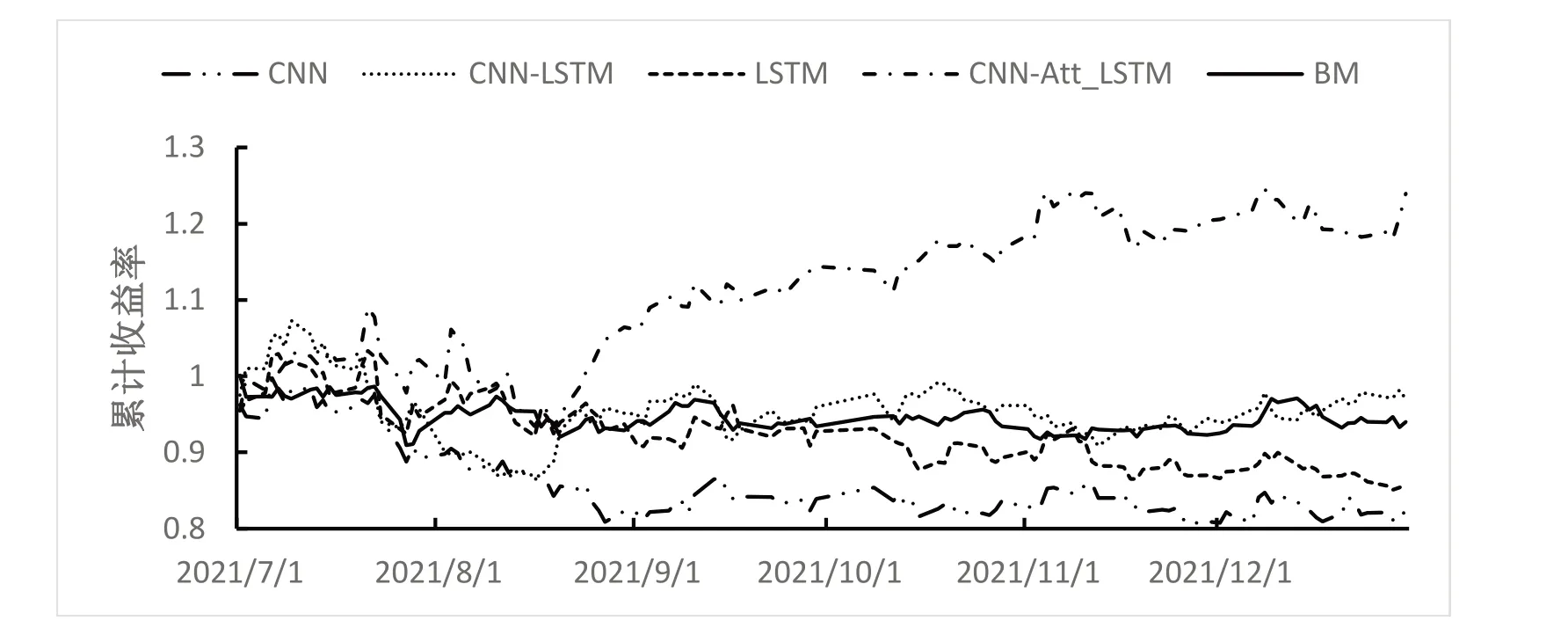
图4 各个预测模型累计收益率曲线

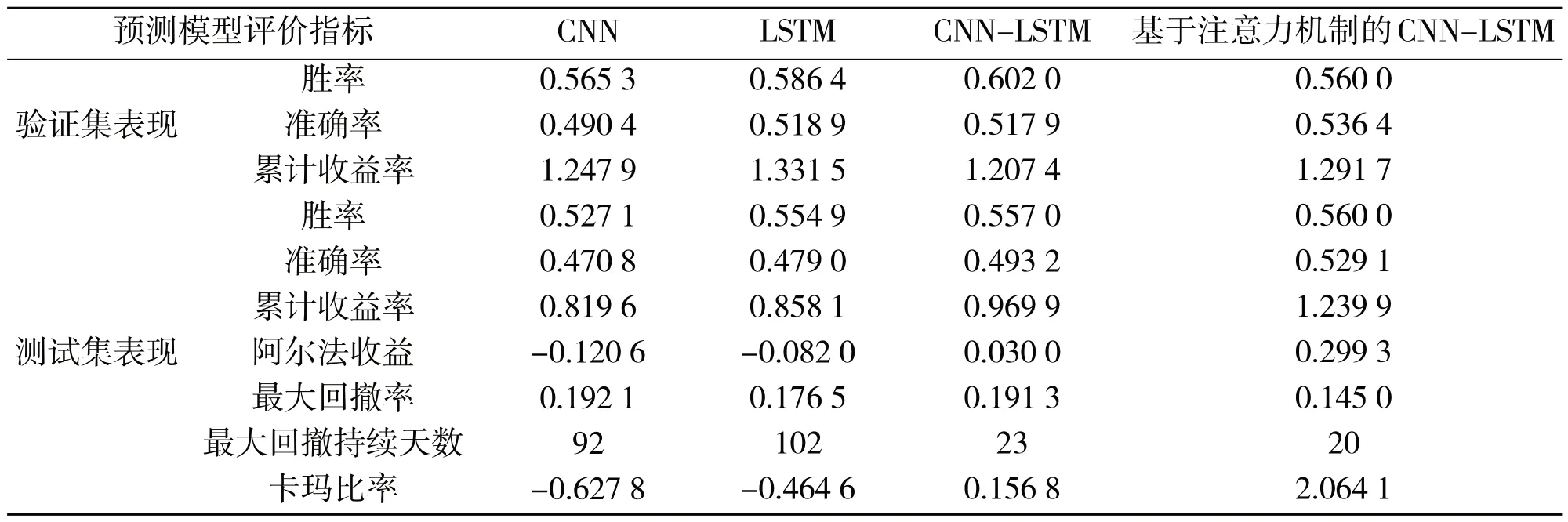
表3 各个预测模型回测结果

由表3 的回测结果可以看出，该文使用的两种复合预测模型均获得了超额收益，其中，基于注意力机制的CNN-LSTM 模型的胜率、准确率、卡玛比率与累计收益率等指标均较CNN-LSTM 模型有所提高，两种单一模型均未获取超额收益，且最大回撤持续天数较长。无论从风险还是收益的角度来看，基于注意力机制的CNN-LSTM模型表现最优。