基于卷积与稀疏编码的半监督学习方法
2022-11-23刘缨杰
刘缨杰,兰 海,魏 宪
(中国科学院福建物质结构研究所泉州装备制造研究中心,福建 泉州 362200)
0 引 言
得益于网络时代数据量的爆炸式增长,深度神经网络模型获得了大量的训练样本,在计算机视觉(CV)领域取得了巨大的进步。但是对海量数据的人工处理必不可少,如训练图像识别和分类网络时需为图像添加对应类别的标签、训练分割任务网络需要为图片中多个物体进行框选标注等。这些基于有标记样本进行训练的模型被称为有监督学习模型,其主要特点在于学习过程依赖于标记信息;同时,无监督学习方法被提出,它们仅使用无标记样本,可以解决标记样本耗费大量人力及时间的问题,但难以应对复杂的CV任务;还有一类模型在训练过程中既利用有标记样本,也利用无标记样本,它们被称为半监督学习[1]。半监督学习一方面利用少量数据所提供的标记信息,另一方面需要充分挖掘全体数据样本的结构、分布信息,使得模型可以更好地完成任务。利用半监督学习算法解决实际的计算机视觉问题极具意义,它也得到了广泛的关注和研究。
半监督深度学习方法已经有了优异的表现,如:MeanTeacher[2]、MixMatch[3]、ReMix[4]、FixMatch[5]和CoMatch[6],这些模型精度的提高依赖于其训练时对未标记样本添加标签的准确性[3]。MixMatch、ReMix、FixMatch等工作基于一致性准则,通过改进和利用不同的数据增广方式,进一步提高了模型性能;CoMatch对分类概率施加平滑约束而生成更好的伪标签,并结合了图方法以计算增广样本和原始样本的嵌入表示。深度学习模型通过提取图像的深层语义特征提高对未标记样本的分类准确度,但它们往往需要进行大量的训练。
研究如何使模型更好地学习到强判别性特征具有重要意义。基于此,本文回顾了半监督学习的一种重要范式——半监督字典学习。字典学习方法在学习图像样本鉴别信息的突出表现使其受到了广泛的关注。图像虽然为高维信息,但其判别信息由少数的特征决定,具有稀疏的潜在特性。因此,通过字典学习构造过完备字典,可将图像信息描述为少量字典原子的线性组合,即获得图像的稀疏表示。稀疏表示拥有更强大的表达能力,包含了可供识别和约束的信息,若将其嵌入更低维特征空间,处理速度更快,在完成半监督任务时也有出色的表现。例如SSR-D[7]将无标记样本归为一类,引入l2,0+范数字典约束项,增强字典学习的鲁棒性,且从输入数据中自适应字典尺寸;由于前者的无标记样本总是对应共享字典的一部分原子,而未考虑其实际所属的类别,SSP-DL[8]为无标记样本构建字典,并预测类别,进一步发掘有标记和无标记样本之间的结构关系;SSD-LP[9]分别学习有标记样本和无标记样本的字典,其中无标记样本的标签通过标签传播的方式获得;DSSDL[10]引入熵正则化避免过度重视无标签数据中不确定的预测的类别。显然,稀疏字典学习方法可以从未标记数据中学习良好的可鉴别的稀疏编码表示。本文希望通过联合卷积神经网络和稀疏编码的优势,高效挖掘图片数据中的潜在判别性特征。文献[11]将全连接层和激活函数替换为字典学习层;文献[12]提出了一种多层的字典学习模型DDL,旨在学习到数据固有的深层结构;文献[13]中所提DDLCN则将卷积层全部替换为字典学习,并在字典学习层前采用额外的特征提取器提取原始图像的特征,组成一个深度字典学习的模型;文献[14]将卷积神经网络和稀疏字典学习相结合应用在高光谱图像分类上,但却仍为简单的两阶段学习,没有形成一个端对端的学习框架。可以发现,目前将稀疏编码和深度学习相结合的相关工作中鲜有研究将此思想拓展应用至半监督学习,以提高模型在半监督分类任务中的性能表现;同时,这些框架在更新参数时,大多仅在欧氏空间求导获得相应的梯度,并未将参数约束项带来的几何上的影响考虑在内;或是加入稀疏编码学习部分后,网络梯度自动传播机制被破坏,使得无法端对端训练深度神经网络,增大了训练的难度。
本文基于文献[15]工作中稀疏表示可微性的研究,实现自稀疏编码至卷积神经网络的梯度传递,进一步探索字典学习和卷积神经网络的潜力。字典学习的输入为深度神经网络提取到的样本特征;字典学习同卷积神经网络联合更新,两者结合为一个端对端框架,并称为Semi-supervised Learning based on Sparse Coding and Convolution(SSSConv)框架。本文联合卷积神经网络和稀疏编码充分提取和学习到图像样本中的鉴别性特征,尽可能保留样本中全局和局部的结构信息,进一步提高模型在下游任务如半监督分类任务中的表现。
1 算法描述
1.1 基于卷积神经网络的半监督深度学习方法和稀疏编码
卷积神经网络是当今最为流行的机器学习模型之一,其核心为卷积运算操作,这也是与其他神经网络和机器学习方法的主要区别。深度卷积网络一般指卷积层较多、深度较深且结构较为复杂的卷积网络模型。自AlexNet[16]被提出后,许多优秀的深度卷积网络随之而生,或改进网络结构,或加深网络深度。目前,诸如VGGNet[17]、深度残差网络ResNet[18]依然是被广泛应用且表现优异的卷积神经网络模型,同时也衍生了大量变种模型,如更宽的残差网络WideResNet[19]、更深的残差网络[20]及ResNeXt[21]等。其中有大量基于卷积神经网络[2-6,22-25]的半监督深度学习方法,如MeanTeacher[2]、MixMatch[3]、ReMix[4]、FixMatch[5]和CoMatch[6]中所提出的半监督模型以WideResNet或ResNet为骨干网络。
研究认为,图像作为自然信号,可以在一个过完备字典上稀疏线性表出,相应的线形组合表达形式被称为图像的稀疏编码或稀疏表示。字典学习算法通过不断交替更新稀疏编码和字典,直至满足迭代要求如迭代次数或重构误差阈值。其中,将求取数据稀疏编码的过程称为“稀疏表示学习”,强调样本可以拥有更为稀疏的表示形式,探索样本在已有字典下的最近似稀疏解(即重构误差最小);“字典学习”则侧重于学习得到能将普通稠密数据表征为稀疏编码形式的字典。因此有稀疏表示学习的目标方程如下所示:
(1)
其中,X=[x1,x2,…,xn]∈m×n为原始数据(即给定的样本),m和n分别表示样本维数和样本数量;Φ=[φ1,φ2,…,φn]∈Q×n为稀疏编码,g(φi)为对稀疏编码的约束条件;D=[d1,d2,…,dn]∈m×Q为字典,Ω为对字典的约束;为避免所得字典的原子(D的列)中元素为无穷大,本文又将字典D的原子di的范数进一步约束至1,即可以认为字典位于Q乘m-1维度的斜流形(Oblique Manifold)之上,因此有:
(2)
本文对稀疏编码Φ的约束为弹性网络(Elastic Net)约束[25],即:
(3)
此时,稀疏编码的优化问题为:
(4)
当稀疏正则项如式(3)所示时,可保证式(1)为严格凸,这使得稀疏编码优化问题成为显式的最小化问题,有助于学习到合适的稀疏表示解,且该解具有唯一性。
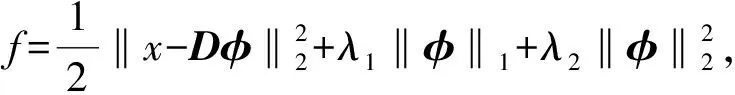
(5)
其中,Λ为φ中非零元素所在位置坐标。综上,稀疏编码模型为:
(6)
字典学习(稀疏表示学习)算法具有很强的信息提取能力,能够在分类任务中为模型提取得到数据的判别性特征表示。
1.2 框架结构
本文基于卷积神经网络和稀疏编码,提出一种将两者相结合,应用于半监督学习和分类任务的端对端训练框架。所提算法一方面可以利用卷积神经网络提取图像特征高层语义信息的能力;另一方面,稀疏编码在良好表示网络所提取特征的同时,具备了更强的可判别性,半监督学习模型能够更好地利用无标记样本,输出的分类结果也更为准确。
基于卷积与稀疏编码的半监督分类框架的基本结构如图1所示。
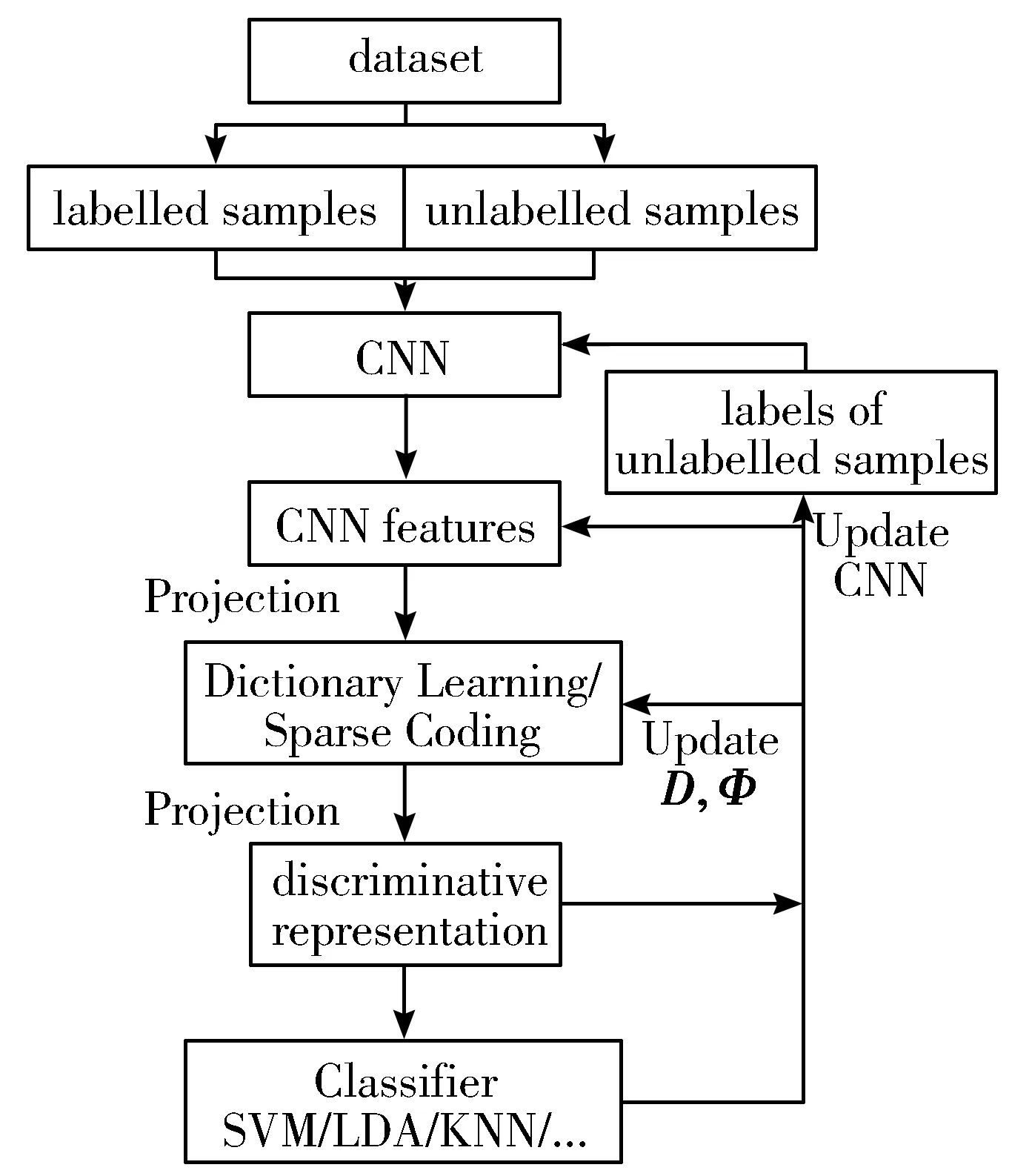
图1 SSSConv结构图
由图1可知,所提框架的图像分类流程:首先输入图像数据,由卷积神经网络最后一层卷积层输出特征信息;对该卷积特征进行正交映射以降低维度,同时将每个样本的特征进一步展开为列向量,组合得到一个特征矩阵;求解字典,获得特征矩阵的稀疏编码,并再次利用正交映射进行降维;最后输入分类器中,得到分类结果。该框架的更新流程将在下文中详细介绍。
1.3 算法优化策略及其梯度传递
1.3.1 损失函数
通过卷积神经网络获得图像的CNN特征矩阵,假设对其正交映射后得到X=[x1,x2,…,xn]∈m×n,根据Φ求取其稀疏编码Φ。则可以利用迹商准则进一步完成如图像分类等任务。迹商最大化问题如下:
其中,tr(·)表示求迹操作。迹商模型被构造为广义的奇异值问题,通过寻找最优映射矩阵V,使得稀疏编码在分布上尽量能够类内相聚、类间分开,这与构建类内散度矩阵和类间散度矩阵本质是一致的。令U位于斯蒂弗尔流形,即S(K,Q):={U∈Q×K|UTU=IK}(Stiefel Manifold),V=UUT最优解非唯一[26],位于m维实数空间的低维线性子空间集之中,即格拉斯曼流形G(K,Q):={UUT|U∈U(K,Q)}(Grassmann Manifold)。
A、B是关于稀疏表示的函数,当它们关于字典D以及样本X可导时,该损失函数可导。A、B一般为上三角半正定矩阵,其构造方法需要根据投影算法不同进行变化,本文以线性判别分析(Linear Discriminant Analysis, LDA)算法为例,有:
B=Φdiag(Πn1,0,,…,Πnc,0)ΦT
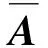
(7)
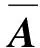
(8)
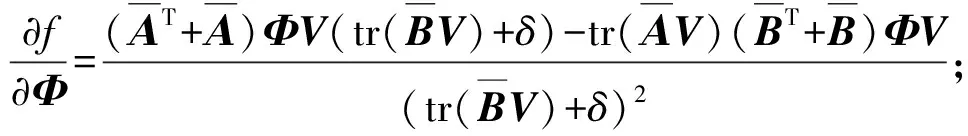
获得稀疏编码后,可再次对其降维,借此进一步到达更低维度的分类空间以降低计算量,随后利用如LDA、SVM等方法进行分类,即通过有标记样本特征的稀疏编码的低维嵌入表示和标签进行聚类拟合后,进一步预测无标记样本的标签,并将其作为当前迭代无标记样本的真实标签。此时可以计算无标记样本的损失值Lossu2,并传入网络模型更新参数。Lossu2可写为:
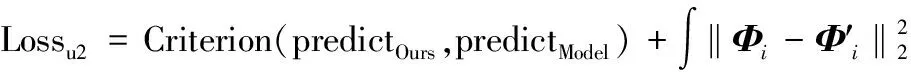
(9)
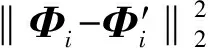
Lossunlabeled=aLossu1+bLossu2
(10)
其中,a、b分别为两者的权重系数。最终模型传入的损失值为:
Loss=w1Losslabeled+w2Lossunlabeled
(11)
其中,w1、w2为有标记样本损失值和无标记样本损失值的权重系数。这部分的损失值直接传入骨干模型即卷积神经网络中。
1.3.2 字典、映射矩阵的几何优化
1.3.1节介绍了本文提出框架所涉及的损失函数。对于神经网络,在设定损失函数或传入损失值后,即可通过梯度回传机制更新其所含参数。对于字典D、映射矩阵V,它们被约束在黎曼流形上,本文采用几何共轭梯度优化方法进行更新。首先计算相应的欧氏梯度,对映射矩阵V的欧氏梯度为:
(12)
(13)
此时,可得∇f(D)。
设乘积流形M:=O(m,Q)×G(K,Q),且C:=(D,V),则点C处切空间可表示为TCM:=TDO(m,Q)×TVG(Q,K);C处黎曼梯度满足〈gradf(D,V),H〉=(Df(D),Df(V))[H],∀H∈TCM。本文将损失函数定义在黎曼流形上全局可微,而黎曼流形可视作欧氏空间的嵌入子流形,因此通过将标准欧氏梯度(∇f(D),∇f(V))正交投影至相应的黎曼流形的切空间[28],解得黎曼梯度。已知斜流形上Y点所在切空间TYO:={X∈m×q|ddiag(YTX)=0}及格拉斯曼流形上Y点所在切空间TYG:={YX-XY|X=-XT}中均有内积运算〈X,Y〉=tr(XTY),结合黎曼梯度性质,可得正交投影操作projDY(·):TYO及projVY(·):TYG以及黎曼梯度如下所示:
(14)
式中ddiag(·)表示取矩阵的对角元素为一个对角阵;projDY(·):TYO和projVY(·):TYG可分别将欧氏梯度正交投影至斜流形上Y点所在切空间TYO和格拉斯曼流形上Y点所在切空间TYG。
利用黎曼梯度和向量传输(Vector Transport)操作TC0,HM:TC0M→TC1M构成新的方向向量H,参数依此方向在切平面上进行移动;回缩(Retraction)操作ΓCM:TCM→M将位于切空间的C点平滑映射回到流形,得到更新之后的参数。
(15)
在乘积流形M上有:
(16)
其中,t为步长,需大于零;(·)Q及(·)R表示QR分解所得矩阵。
图2为流形上回缩操作和向量传输操作示意图。
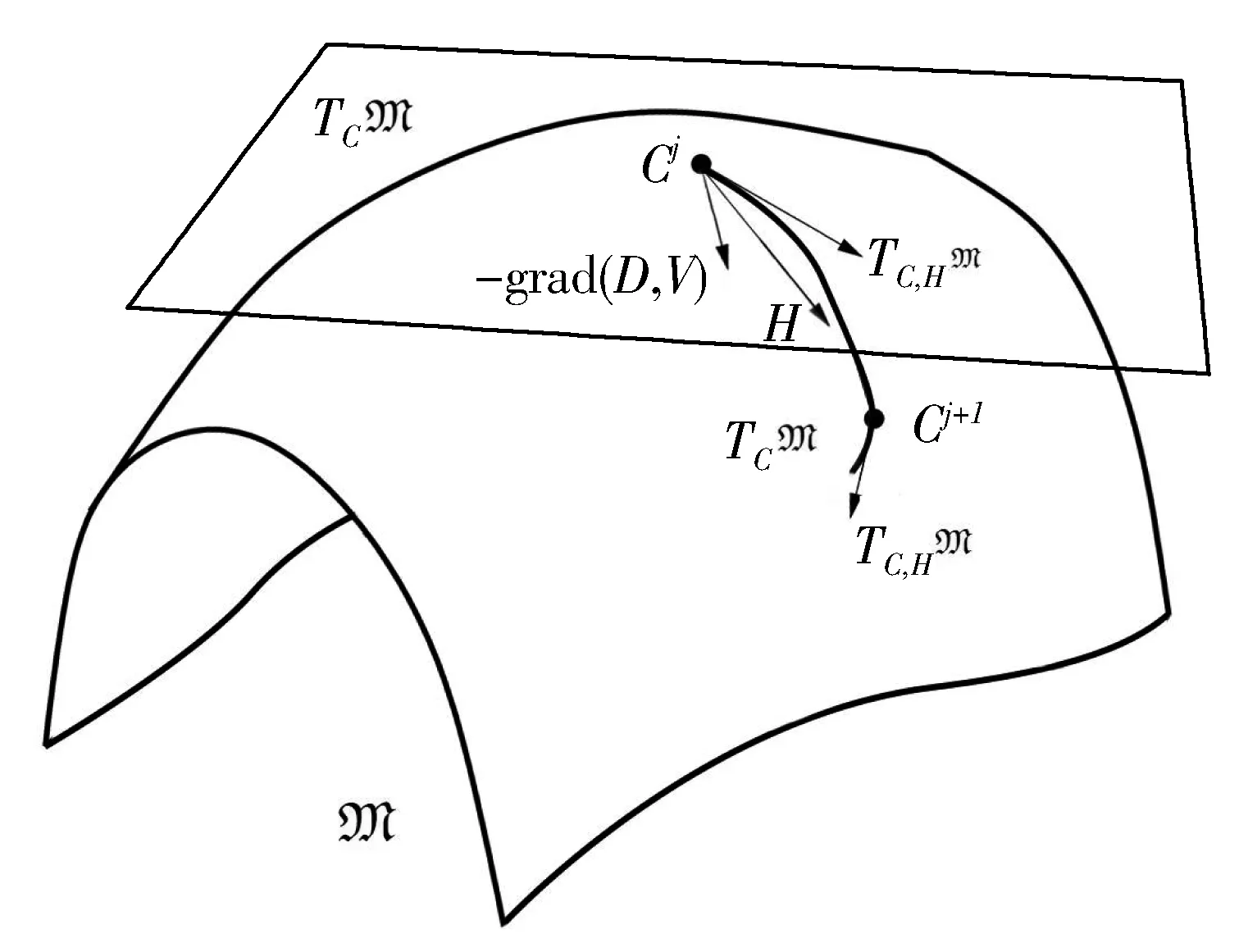
图2流形上回缩操作和向量传输操作示意图
在流形上的共轭梯度更新流程如下:
2)已知∇f(Dj)和∇f(Vj),根据式(14)计算对应黎曼梯度gradf(Dj,Vj);当j=0时,H0=-gradf(C0)。
3)根据式(16)所求回缩操作ΓCM变换得到新Dj+1,Vj+1,即Cj+1=(Dj+1,Vj+1),已知新字典,同时求取对应的稀疏编码;此外,通过向量传输操作TCj,HjM,得到Hj+1=-gradf(Cj+1)+βTCj,HjM;为使TCj,HjM与
HessianCjf共轭,令:
1.3.3 算法实现
本文所提方法可实现端对端的半监督分类学习模型训练,在训练过程中,所加载数据包含了有标记样本和无标记样本。模型结构如图1所示,训练步骤如下:
1)在进行图像预处理后,将样本送入半监督卷积神经网络中,除了得到predictModel,还从最后一个卷积层输出网络所提取的特征。
2)对卷积特征进行正交降维映射后,进行字典学习并获得相应的稀疏编码,求取稀疏编码的正交映射低维稠密表示,并进一步通过分类器得到分类结果predictOurs。
3)根据式(6)、式(8)和式(11),计算梯度和损失值,分别更新字典、稀疏编码、映射矩阵、以及半监督神经网络的参数,其中字典的更新和映射矩阵的更新详见1.3.2节介绍的流形参数共轭梯度更新流程。
4)重复以上步骤,直至达到最大更新迭代次数或损失值收敛。
2 分析与讨论
为验证本文所提框架的有效性,本文在公开图像数据集CIFAR-10、SVHN及CIFAR-100上进行实验。由于FixMatch为目前表现最为优异的半监督学习方法之一,同时作为半监督深度学习方法,相较于半监督字典学习如OSSDL、SSP-DL、SSD-LP等已经有了极大的提升,因此,本文实验主要同MixMatch、ReMixMatch及FixMatch进行比较。同时,本文所提方法将主要以MixMatch和FixMatch为骨干模型进行,在下文分别简写为Ours(-MixMatch)和Ours(-FixMatch),或SSSConv(-MixMatch)和SSSConv(-FixMatch)。表1为实验所用数据集。
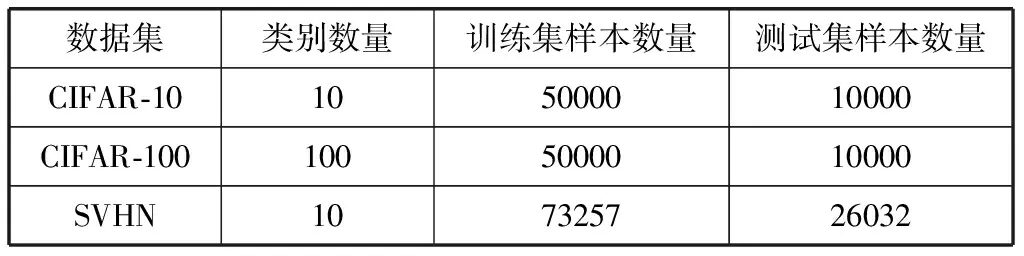
表1 实验所用数据集
2.1 参数设置和实验环境
本节将介绍框架骨干神经网络和字典学习(稀疏表示)的相关参数,并进一步确定关键参数的取值。用于半监督学习的卷积神经网络的超参数依然有学习率和训练样本的batch大小;在训练过程中,学习率设置从0.01开始,均结合动量项0.9;训练样本的batch大小均设置为64。学习字典和稀疏编码的过程中主要有4个参数,分别为稀疏约束项参数λ、字典的第二维度大小Q、初始化字典所用样本数量N,以及字典初始化时更新迭代次数t。其中,字典更新迭代次数由重构误差进行判断,如图3所示,当t大于10时,误差变化幅度极小,如当字典第二维度大小设置为2048时,平均重构误差最小。
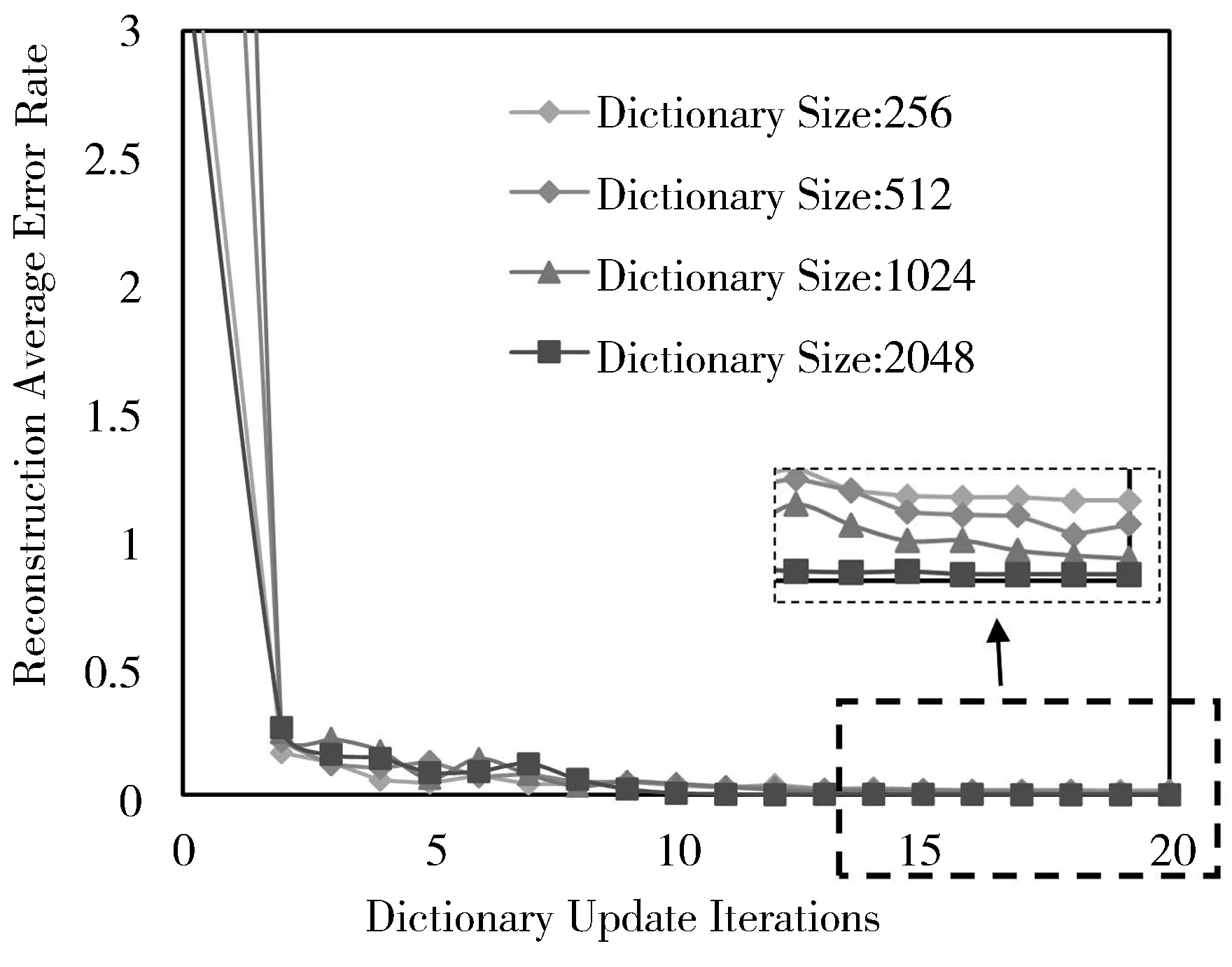
图3 迭代次数t与字典大小对稀疏编码重构误差的影响
同时,以CIFAR-10为例,设置λ从0~1取值,N和Q从1000~50000中取值,通过网格搜索确定3个超参数的最佳配对(N,Q,λ),以获得最佳的分类精度。可以发现,当稀疏约束项参数取值0.1~0.2,字典第二维度与初始化字典所用样本数量相等且每类样本尽量多时,精度较高。但由于字典维度越大,需要的计算量越大,综合考虑性能和效率,本文将减少一定的字典维度和训练字典所用样本的数量。
2.2 实验结果
本文在CIFAR-10、SVHN及CIFAR-100数据集上进行实验,同MixMatch、MixMatch的改进版本ReMixMatch,以及如今性能最为优异的FixMatch方法进行比较。实验中所有模型的最大训练迭代次数均为1024;模型精度指其在测试集中进行5次实验后所得的平均分类准确度。
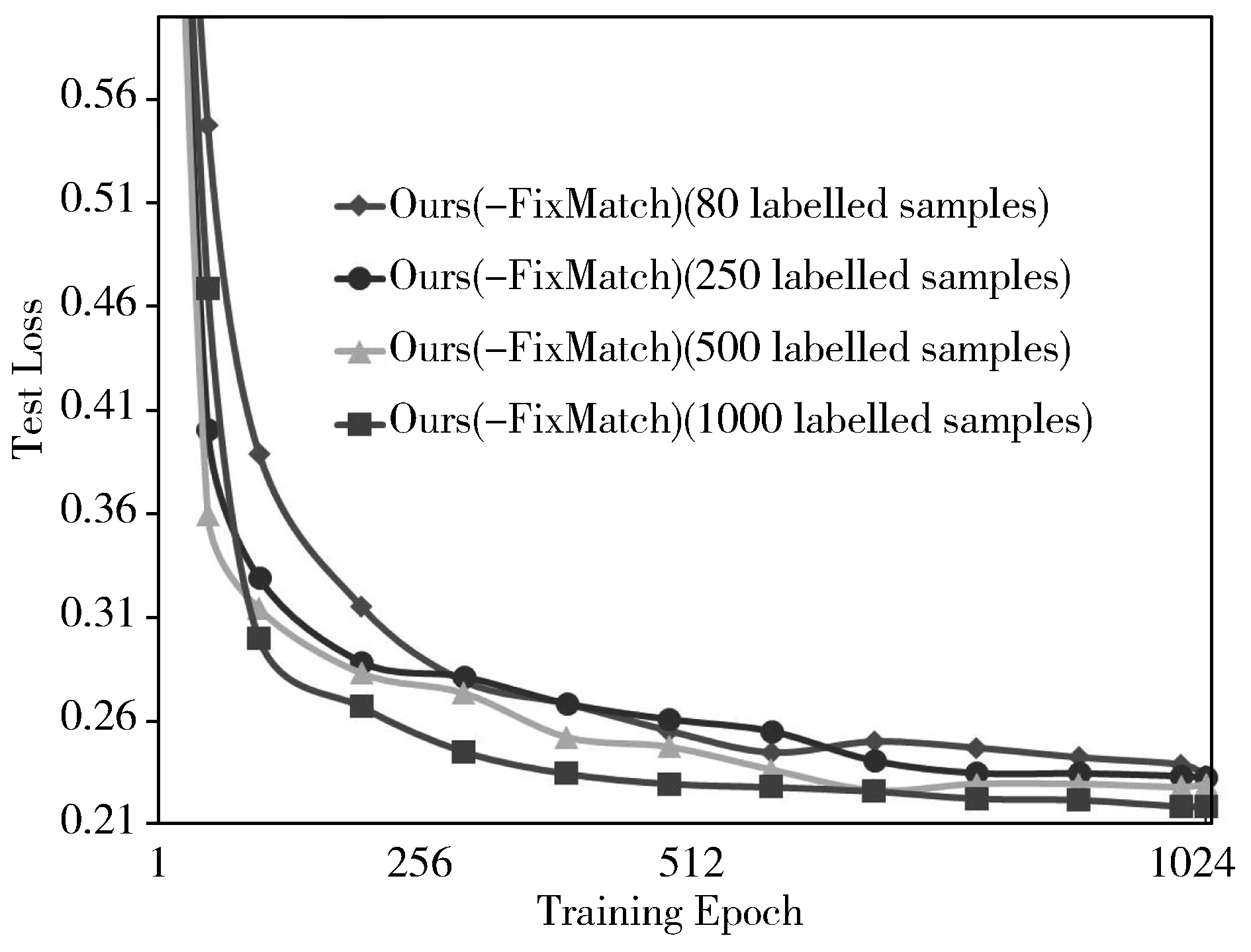
(a) 测试损失值
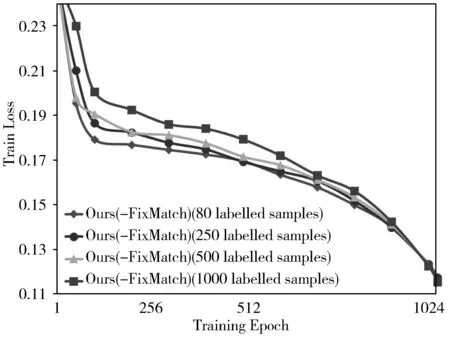
(b) 训练损失值图4 本文所提Ours(-FixMatch)在CIFAR-10数据集上的的收敛曲线
1)CIFAR-10包含10个类别的60000张图像,每类6000张,图像尺寸均为32×32。训练集和测试集分别为50000张和10000张,每类所含图像数目一致。实验结果如表2所示,每次实验随机选取CIFAR-10中的80、250、500及1000个训练样本作为有标记样本,其余训练样本为无标记样本,剩余的全部作为测试样本。在CIFAR-10数据集中,SSSConv的半监督分类精度平均提高了0.50个百分点;当有标记样本数量为80时,本文所提模型相较于此前SOTA模型提升最大,为1.35个百分点;当有标记样本为250时,Ours(-FixMatch)的分类精度已经比有标记样本为500时的原SOTA精度95.42%更高;且经测试,有监督学习ResNet-34精度为95.69%,可见当有标记样本数量为1000时,Ours(-FixMatch)(即SSSConv(-FixMatch))为95.64%,相差不到0.1个百分点。
2)图4可视化了数据集为CIFAR-10时本文所提框架Ours(-FixMatch)优化过程的收敛曲线,其中图4(a)为测试的损失值,图4(b)为训练的损失值。同时,可以发现,模型训练刚开始时,训练损失值和测试损失值均迅速下降,随着训练进行,训练损失值下降放缓,测试损失值始终保持下降趋势。当训练迭代次数接近设定阈值1024次时,模型的测试损失值同训练损失值接近,且变化幅度较小,说明模型达到了良好拟合的状态。卷积神经网络在联合稀疏编码的过程中,目标一致,有效地提高了学习模型的分类性能。
3)从图5和图6可以发现,MixMatch和FixMatch结合本文所提方法(即Ours(-MixMatch)和Ours(-FixMatch)后,训练过程中的分类精度和最终的分类结果均优于骨干模型(MixMatch和FixMatch)。在有标记样本数量较少时,本文所提框架表现优异,尤其在训练初期,模型的测试精度提升速度有显著的提升,如CIFAR-10中有标记样本数量为80时,本文所提方法Ours(-FixMatch)比其骨干网络FixMatch方法提升精度达到5个百分点。结果表明本文所提算法框架有效,其获得的图像表示具有更强的可鉴别能力,提高了分类器的分类性能,赋予未标记样本的标签也更为准确,有效地提高了骨干模型的性能表现。
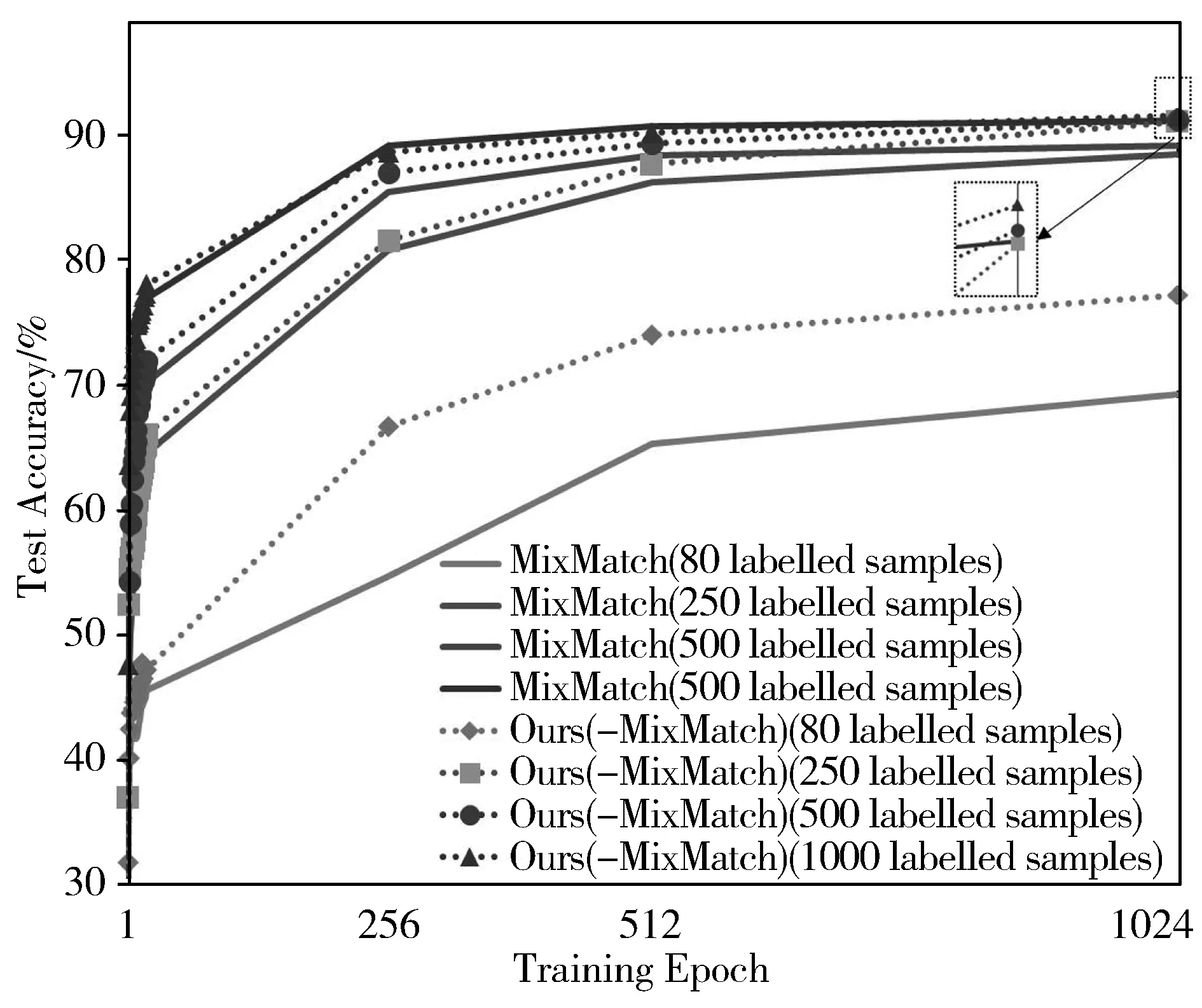
图5 MixMatch及本文方法的测试精度变化曲线(CIFAR-10)
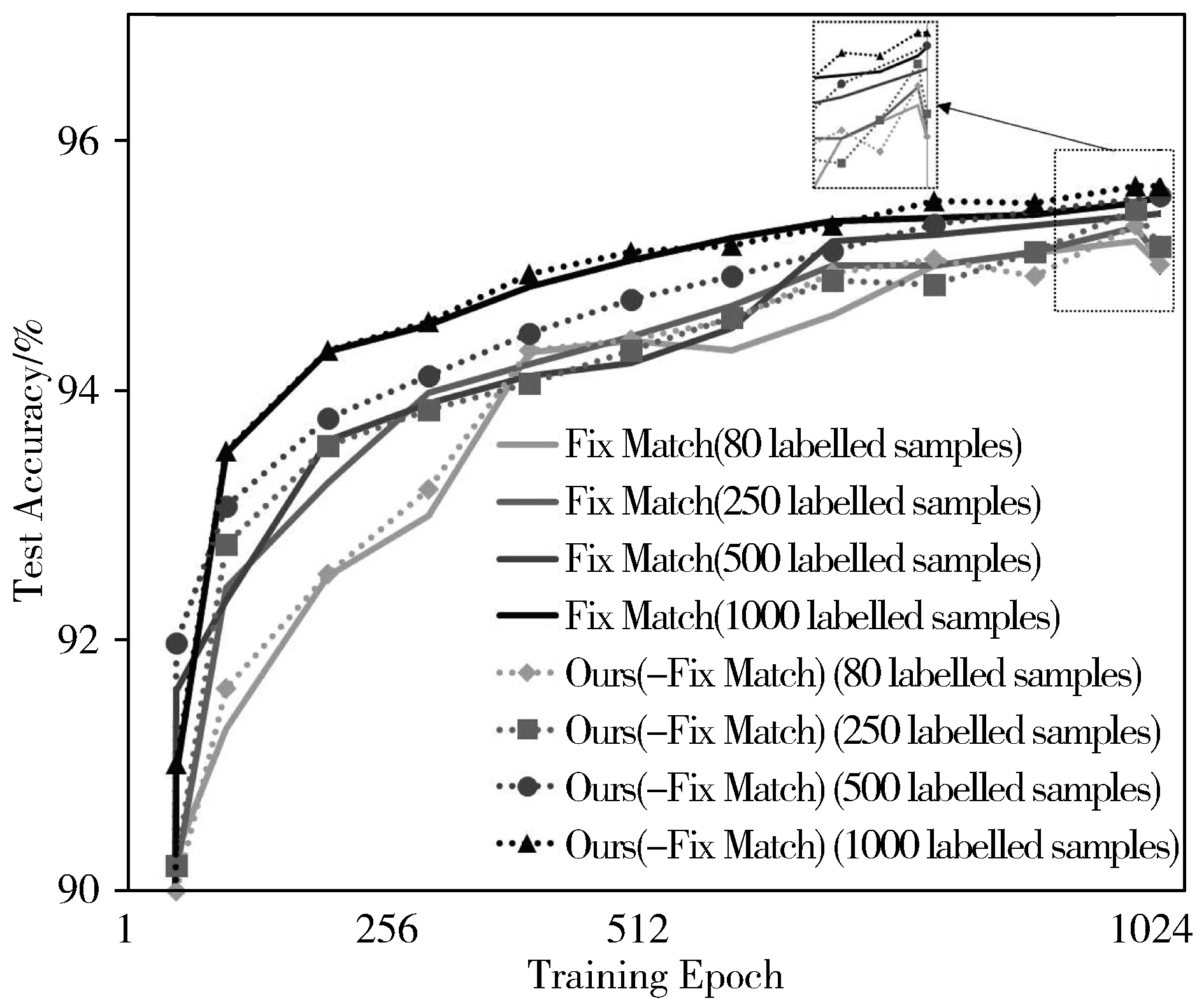
图6 FixMatch及本文方法的测试精度变化曲线(CIFAR-10)
4)表3展示了本文所提框架SSSConv(-FixMatch)在SVHN数据集和CIFAR-100数据集中的精度表现。SVHN和CIFAR-10均含有10个类别;其图片是来源于谷歌街景门牌号码,为32×32彩色图片,有73257张用于训练,26032张用于测试,还包含有531131个数字额外数据集,额外数据集在本文中未使用;CIFAR-100则包含100个类别,训练集和测试集分别有50000张和10000张。本文在实验中随机从SVHN的训练集中选取40张、250张、1000张图片作为有标记的训练样本,其余的为无标记训练样本,测试集不变,仍为10000个测试样本;在CIFAR-100的实验中,随机选取400、2500、10000个样本进行半监督实验。本文所提算法首先对卷积特征进行稀疏编码,并利用正交映射降低编码维度,充分利用了无标记样本和有标记样本的结构信息;在SVHN中平均提升了0.54个百分点的准确度,CIFAR-100中平均提升了0.49个百分点,其中当有标记样本数为2500时,提升了0.69个百分点。实验结果再次表明本文算法对现有的半监督方法有显著的提升效果。
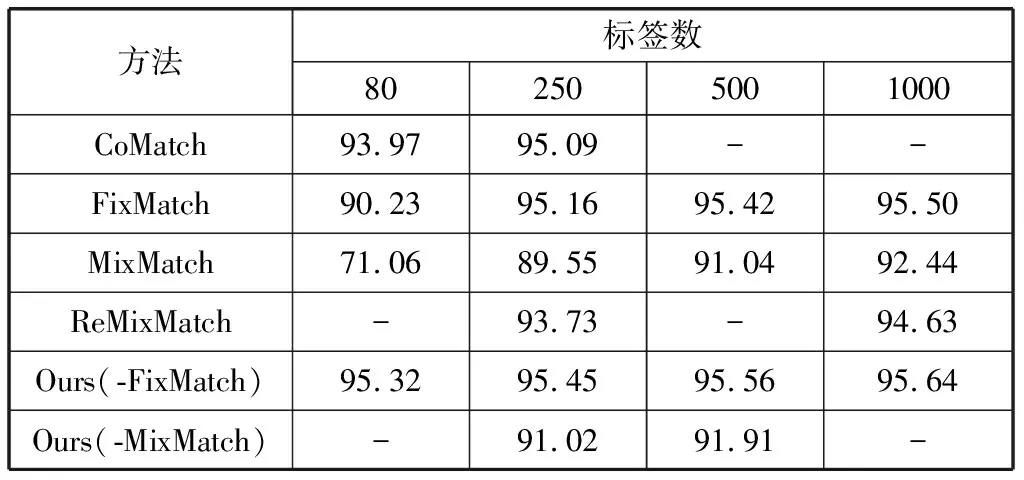
表2 CIFAR-10训练集中分别有80、250、500、1000个样本为有标记样本时的分类精度 单位:%
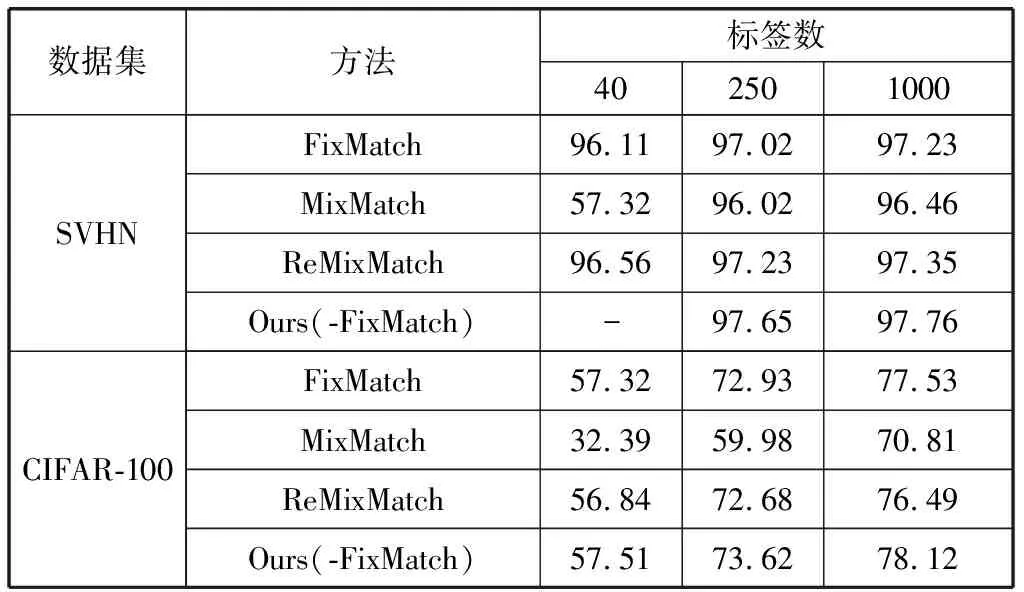
表3 SVHN训练集中有40、250、1000个有标记样本时的分类精度与CIFAR-100训练集中有400、2500、10000个有标记样本时的分类精度 单位:%
3 结束语
本文提出了一种基于卷积神经网络和稀疏编码的端对端半监督学习方法,首先通过研究稀疏回归解的可微性,并进一步设计统一损失函数、推导参数梯度以解决稀疏编码字典学习部分与半监督卷积神经网络部分间的梯度传递问题,实现端对端训练,最后结合两者的优势提高了模型框架在半监督分类问题的表现。实验结果表明,该结构可以很好地适应现有的先进的半监督深度学习方法,在分类任务中表现优秀,具有竞争力。
