例谈递推公式an+1+an=f(n)中不同类型的f(n)问题
2022-11-23江苏省白蒲高级中学柳永红
江苏省白蒲高级中学 柳永红
1 f(n)为一次函数型
当递推关系an+1+an=f(n)中f(n)为一次函数形式时,利用分组求通项公式再求和的方法求解.一般根据题目条件分n为奇数和n为偶数分别求通项公式,再将其合并整理得对应的数列通项公式.利用此方法求解通项公式的解题步骤为:①根据实际条件,确定所求数列的类型,并求其首项和公差(或公比);②利用已知的首项,公差(或公比)的值,分n为奇数和n为偶数讨论并求得对应的通项公式;③将上述所得结果合并整理,即得数列的通项公式.
例1已知数列{an}满足a1=2,an+1+an=4n+3,求数列{an}的通项公式.
分析:首先利用an+1+an=4n+3表示出an+1+an+2=4n+7,确定数列{an}的奇数项、偶数项分别构成公差为4的等差数列,再由此分析n分为奇偶数时的通项公式,即an=2n和an=2n+1,最后整合得数列{an}的通项公式.
解:由题意可得
an+1+an=4n+3 ①
an+1+an+2=4n+7 ②
②-①,可得an+2-an=4.
所以,数列{an}的奇数项和偶数项分别构成公差为4的等差数列,且a2=5.
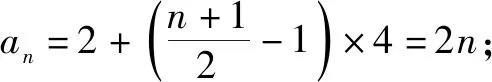
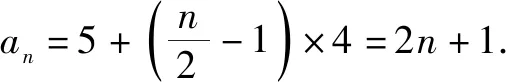
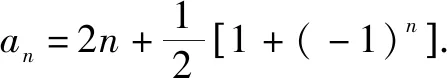
变式1已知数列{an}满足a1=1,an+1+an=-4n+1,求数列{an}的通项公式[1].
分析:该变式与例1略微不同,即f(n)=-4n+1,但解题思路仍与例1一致.
解:由题意可得
an+1+an=-4n+1 ③
an+1+an+2=-4n-3 ④
②-①,可得an+2-an=-4.
所以,数列{an}的奇数项和偶数项分别构成公差为-4的等差数列,且a2=-4.
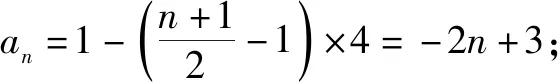
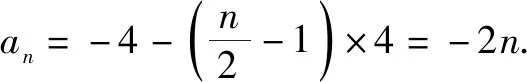

2 f(n)为指数型
当递推关系an+1+an=f(n)中f(n)为指数型时,求其通项公式可以利用分解变量构造等比数列,将已知的递推关系an+1+an=f(n)分离变量,得到an+1-k·f(n+1)=-[an-k·f(n)](k为常数),再利用等比数列{an-k·f(n)}的通项公式求解.利用此方法求解通项公式,解题步骤为:①结合实际问题,将已知式子分离变量得到an+1-k·f(n+1)=-[an-k·f(n)];②根据上述等式确定等比数列{an-k·f(n)}的通项公式;③利用等比数列{an-k·f(n)}的通项公式求解数列{an}的通项公式.
例2在数列{an}中,a1=1,an+1+an=2n,求数列{an}的通项公式.

解析:令an+1-k·2n+1=-(an-k·2n),则整理为an+1+an=3k·2n.



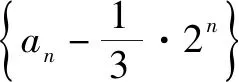
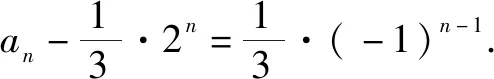
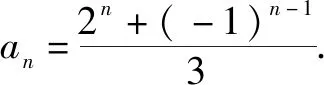
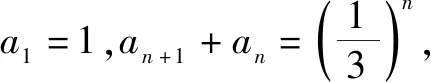

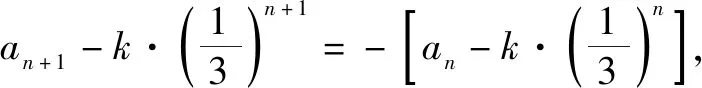
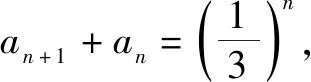
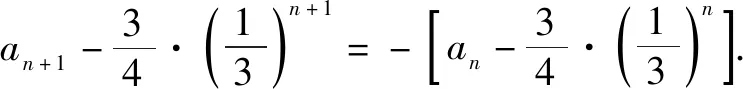

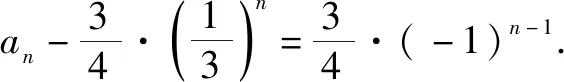

3 f(n)为分式型
求解f(n)为分式型的递推关系an+1+an=f(n)对应的通项公式,裂项并构造是解题的有效手段.裂项并构造,指的是将递推关系an+1+an=f(n)中的分式f(n)进行裂项,并以此构造数列求解.利用此方法求解数列的通项公式,一般的解题步骤为:①根据实际问题中的f(n)的特点进行裂项,变为g(n)-h(n)的形式;②利用裂项所得的式子构造新数列并求解[2].


解:设Sn为{an}的前n项和.由题意,得
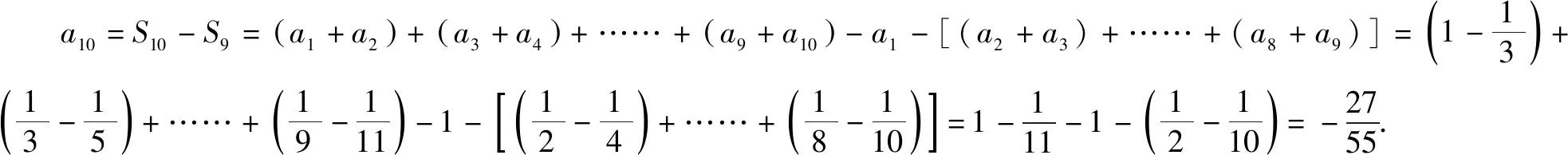
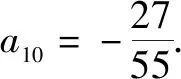

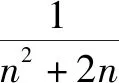

当n=2k(k∈N*)时,
Sn=a1+a2+……+an-1+an
=(a1+a2)+(a3+a4)+……+(an-1+an)

当n=2k+1(k∈N*)时,
Sn=a1+a2+……+an-1+an
=a1+(a2+a3)+(a4+a5)+……+(an-1+an)
所以,当n=2k时,
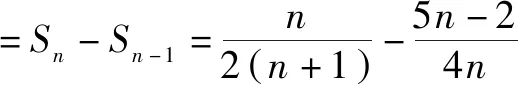
当n=2k+1时,

求解an+1+an=f(n)型的数列的通项公式,具体运用哪种方法求解要根据f(n)的形式确定.总之,与an+1+an=f(n)有关的递推关系中,f(n)涉及的类型主要为本文中所介绍的一次函数型、指数型和分式型,其中一次函数型和指数型都可以利用分组求通项然后合并的方式求解,视实际情况而定.解题时,不仅要掌握形如an+1+an=f(n)求通项公式这一类问题的答题思路,还要做到灵活变通,对不同的递推公式采取不同的解题策略.
