一种基于极限学习机融合模型的实时亚表面缺陷深度检测算法

王章权周 莹周煊勇刘半藤*

(1.浙江树人大学信息科技学院，浙江 杭州 310000；2.常州大学信息科学与工程学院，江苏 常州 213000)

当对导体亚表面缺陷深度进行检测时，脉冲涡流(Pulsed Eddy Current，PEC)检测和超声波(Ultrasonic，UT)检测是两种常用的无损检测方法[1]。脉冲涡流检测对导电结构表面浅层缺陷检测能力较强，但对更深缺陷的检测能力显得较弱；然而，超声波检测则较难检测表面浅层的缺陷，更适用于检测更深的缺陷。虽然单一检测方法无法满足各类深度缺陷的检测需求，但是两种检测方法具有一定互补性[2-4]。因此，研究基于脉冲涡流和超声波的复合检测方法对导体亚表面缺陷进行检测显得更有意义。此外，由于铁路轨道、飞机亚表面等环境对检测时效有较高要求，设计一种实时复合检测方法极有必要!

不少国内外的专家学者对此开展广泛而深入的研究。设计实时亚表面缺陷检测方法的关键在于快速以及准确。由于传统检测方法采用神经网络模型计算缺陷在不同深度的概率分布，该方法计算量较大且复杂度较高，并不适合应用于实时导体亚表面缺陷深度检测。近年来，极限学习机(Extreme Learning Machine，ELM)因其具有良好的收敛性能以及泛化性能，被广泛地应用于各类实时计算。理论研究表明，极限学习机模型随机生成输入权重和隐含层阈值的方法，使其在具有极快学习速度的同时仍保持单隐层神经网络的通用逼近能力。由于极限学习机的运算速度快于传统神经网络，计算精度较传统神经网络略有下降。为提高计算精度，很多学者对极限学习机分类方法进行优化，如通过对极限学习机模型的输入权重和阈值等参数进行优化以达到快速精确分类的效果[5]，这些优化方法以进化算法为主。例如，党建武等人[6]结合果蝇进化算法对极限学习机模型的参数进行修正，提高极限学习机的计算精度。杨辉等人[7]结合粒子群优化算法对传统的极限学习机模型参数进行优化，提高模型的计算精度。由于计算量较大，这些启发式算法也适于实时监测方法。为提高亚表面缺陷的检测精度，需要融合来自于两种不同检测方法的数据(脉冲涡流检测、超声波检测)。D-S证据理论能够将两种不同检测方法的不确定性信息以概率形式融合实现对导体缺陷深度的识别[8-10]。传统D-S理论并没有考虑证据可信度会发生变化的状况[11-12]。但是，对含有不同深度缺陷的导体进行检测时，脉冲涡流和超声波的检测能力有明显差异性，直接进行D-S融合并不能够得到令人满意的结果。为提高亚表面缺陷的检测精度，本文采用动态赋权方法对原始概率分布进行数据处理，再通过D-S融合模型获得最终概率分布，从而实现快速、准确的亚表面缺陷深度检测。

1 基于极限学习机融合模型的缺陷检测算法

为利用脉冲涡流检测以及超声波检测获取的原始数据快速计算导体缺陷在不同深度下的概率分布，本文建立极限学习机模型进行缺陷深度检测。将已知m类缺陷深度按照从浅到深的顺序编号为1，2，…，m。对缺陷深度为1 mm～4.5 mm(每隔0.5 mm)的导体进行实验测试，编号1的深度为1 mm，编号2的深度为1.5 mm，依次类推，编号8的深度为4.5 mm。首先，将N个已知缺陷深度的导体分别经过脉冲涡流检测以及超声波检测，并从两类检测获得的原始数据提取n种特征数据。记，表示第j个导体经过检测获得的特征数据，j＝1，2，…，N；i＝1，2。其中，i＝1表示脉冲涡流检验获得的特征数据，i＝2表示超声波检验获得的特征数据。记Y j＝[y1j，y2j，…，y mj]表示导体缺陷在各类深度的概率分布。

极限学习机模型的输入为导体经过脉冲涡流或者超声波检测获得的特征数据，输出为导体缺陷在各深度的概率分布Y j，数学模型可以表示为[13]:

式中:L表示隐藏单元数量，βl表示第l个隐藏层与输出层之间的权重向量，w l表示传感器探测数据与第l个隐藏层之间的权重向量，g l(x)表示第l个隐藏层的激活函数，b l表示第l个隐藏层的偏置向量。

定义极限学习机的输出矩阵H如下:

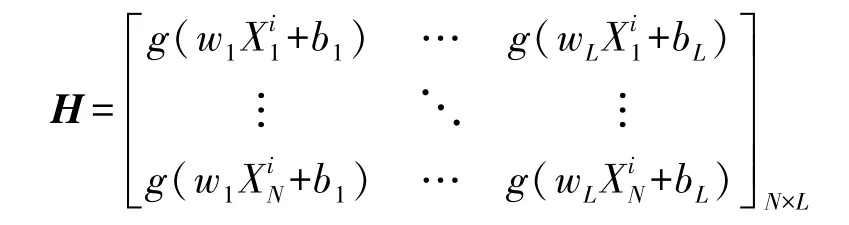
极限学习机模型输入与输出间的关系可以用矩阵表示如下:

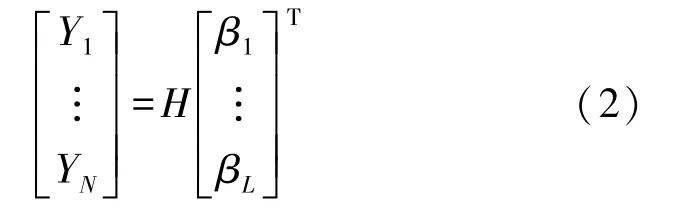
首先，将N个已知缺陷深度的导体分别经过脉冲涡流检测以及超声波检测，获得原始数据的特征数据；然后，将特征数据以及对应的概率分布进行极限学习机训练，从而计算每种检测方式的极限学习机参数。参数计算方法如下:

区别于传统神经网络模型，极限学习机模型的输入层与隐含层的连接权值、隐含层的阈值可随机设定，且设定完后不再调整。当训练脉冲涡流检验获取的特征数据计算极限学习机模型参数，并将其应用于计算未知缺陷深度的导体在各深度下的概率分布时，计算方法如下:

Step 1 整理N个已知亚表面缺陷深度的导体进行脉冲涡流检测获取特征数据，形成训练样本数据库；

Step 2 随机生成权重向量w i、偏置向量b i，隐藏单元数量L；

Step 3 根据权重向量、偏置向量计算输出矩阵的Moore-Penrose广义逆矩阵H＋；

Step 4 采用如下方式计算极限学习机模型参数:

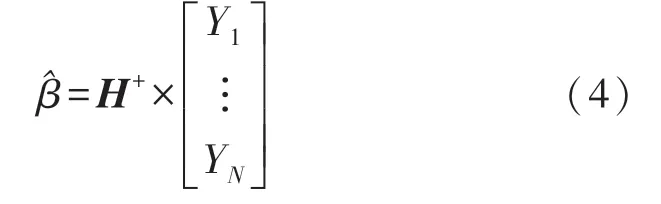
Step 5 对某未知缺陷深度的导体进行脉冲涡流检测，将特征数据输入上述已经完成训练的极限学习机模型得到该样本缺陷在各深度的概率分布。

整理上述N个已知亚表面缺陷深度的导体进行超声波检测，获取特征数据，重复上述Step 1～Step 5可以得到超声波检测的极限学习机模型参数。对某个未知缺陷深度的导体经过上述两个极限学习机进行学习后可得到两种不同的概率分布。记表示第j个未知缺陷深度的导体经极限学习机输出的概率分布。其中，i＝1表示脉冲涡流检验数据经过极限学习机学习获得的概率分布，i＝2表示超声波检验数据经过极限学习机学习获得的概率分布。

基于此，需要设计一种方法将两种不同的概率分布进行有效融合，以便对该导体的缺陷深度进行识别。由于脉冲涡流以及超声波在不同深度的缺陷检测时各具特点:脉冲涡流检测对导电结构表面浅层缺陷检测能力强，对较深缺陷的检测能力显得较弱。因此，脉冲涡流的权重是随着深度加大而变小的函数，定义如下:

式中:表示脉冲涡流检测学习获得概率分布中第i个深度赋予的权重，m表示深度类型数量。

由于超声波较难检测表面浅层的缺陷，更适用于检测较深程度的导体缺陷。因此，超声波的权重是随着深度加大而变大的函数，定义如下:

式中:表示超声波检测学习获得概率分布中第i个深度赋予的权重。

对极限学习机获得的原始概率分布进行加权得到新的概率分布计算方式如下:

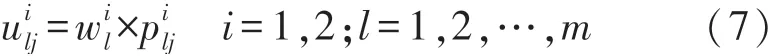
采用D-S证据合模型将上述得到两类概率分布进行融合[14-15]，得到该导体缺陷在各种深度的概率R j＝[r1j，r2j，…，r mj]，融合过程如下:

式中:r i j表示第j个未知缺陷深度的导体缺陷属于第i个深度的概率。

最终，按照最大概率准则将该导体缺陷深度分类至概率最大项，即:

式中:d j表示第j个未知缺陷深度导体的缺陷深度编号。

2 实验与结果分析

为了测试本文提出方法的性能，设计实验，采用厚度为20 mm的铝板作为试件，在导体亚表面加工8种宽度为4 mm、长度为20 mm、深度互不相同的条形缺陷，以及半径为5 mm的圆孔缺陷。缺陷与表面的距离分别为1 mm～4.5 mm，不同缺陷间以0.5 mm差值递增，分别用来代表导体亚表面缺陷中最普遍的裂纹缺陷和腐蚀类缺陷，试件示意图如图1所示。

图1 实验试件示意图

首先，采用脉冲涡流检测仪对该试件进行检测，设置脉冲涡流激励信号频率为100 Hz，幅度为5 V，占空比为50%，采样频率为200 kHz。脉冲涡流设备由信号发生器、信号放大模块和调理模块组成，经由内置NI采集卡获得脉冲涡流信号至上位机，如图2所示。然后，采用超声波仪器对该试件进行检测，采用食用油作为耦合剂，使检测探头与试件紧密贴合，设置采样频率为5 MHz，以单探头工作方式进行发射接收，超声波设备采用TA-3062E型号的双通道超声检测系统，设备如图3所示。

图2 脉冲涡流检测设备

图3 超声波检测设备

本实验采用上述两种检测方法对每组缺陷各检测50组，取两组有/无缺陷的检测信号，分别如图4、图5所示。脉冲涡流在幅值上有明显的差异，超声波在回波时间上亦有明显的差异。

图4 脉冲涡流检测信号

图5 超声波检测信号

通过脉冲涡流实验获得的数据分布如图6所示，可见，3.0 mm深度以下的缺陷信号有明显响应，3.5深度以上的缺陷信号基本无响应，且深度越深的缺陷信号越难以与其他深度下缺陷信号区分；通过超声波实验获得检测信号，并提取第一回波时间如图7所示，可见，缺陷深度越深的第一回波时间越集中，且越容易与其他深度下的回波时间进行区分，4 mm深度以上的超声波信号基本能独立识别。

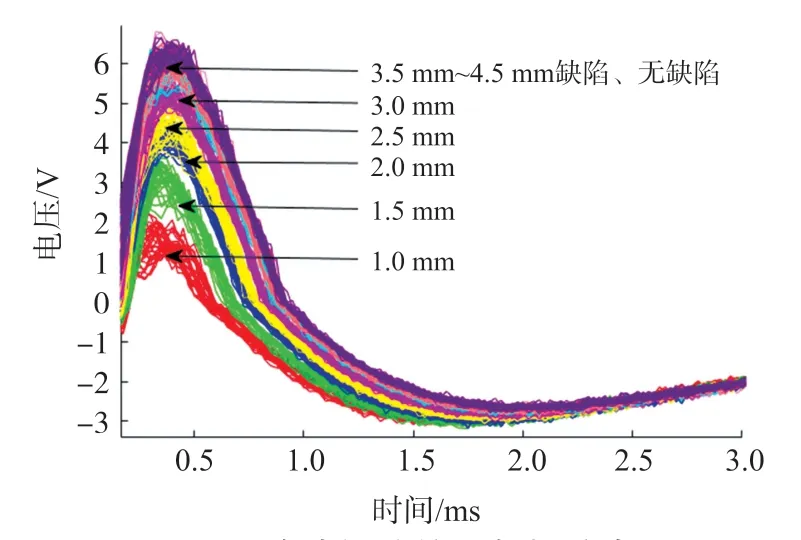
图6 脉冲涡流信号数据分布

图7 超声波第一回波时间分布

将导体亚表面不同缺陷深度的条形缺陷和圆形缺陷通过脉冲涡流和超声波检测，每类缺陷深度各自获得50组数据。每类缺陷深度随机提取25组作为训练集，剩余25组数据作为测试集进行测试。采用极限学习机分类模型获得不同缺陷深度25组独立检测概率，分别将单一检测和复合检测获得的概率分布进行加权计算，获得不同深度下导体亚表面条形和圆形缺陷的量化结果，与实际缺陷深度数据比较获得平均误差如图8、图9所示，均方误差如图10、图11所示，分别用以反映量化准确度以及稳定度。

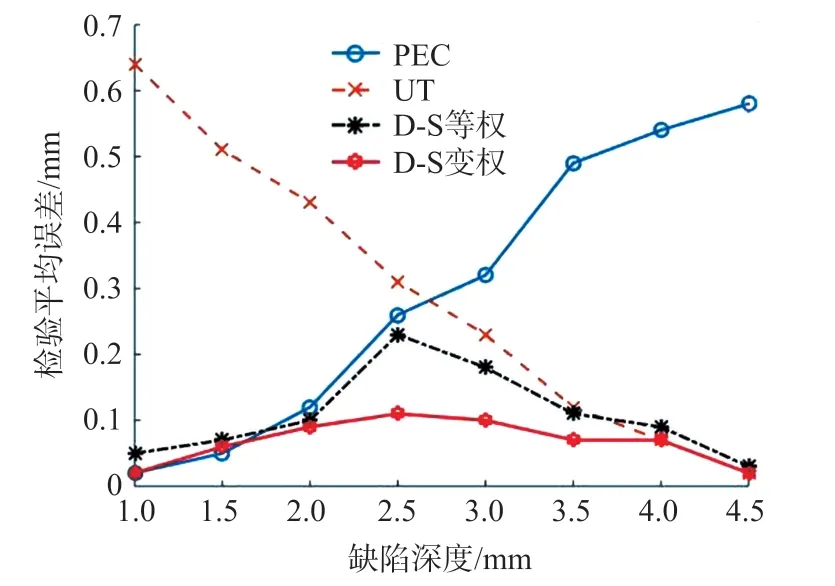
图8 条形缺陷各深度的误差平均值

图9 圆形缺陷各深度的误差平均值

图10 条形缺陷各深度的误差均方差值

图11 圆形缺陷各深度的误差均方差值

可见，对两种深度缺陷在1 mm以下的近表面缺陷，本文算法和独立脉冲涡流检测效果较好；对深度在4 mm以上的深层缺陷，本文算法和独立超声波检测效果较好；对于深度为1 mm～4 mm的亚表面缺陷，本文所提出算法具有最好的检测效果，检测误差在均在0.11mm以内，量化的精确度和稳定性均优于常规D-S证据理论方法和独立检测方法。

3 结论

针对导体亚表面缺陷深度检测的难题，本文提出了一种基于极限学习机融合模型的实时亚表面缺陷深度检测算法。首先，构造极限学习机模型，将涡流传感器以及超声传感器获取的原始数据转化为导体缺陷在不同深度的概率分布；然后，根据不同传感器采集特点对概率分布进行动态加权，并采用D-S融合模型计算最终的概率分布；最后，基于最大概率原则对未知缺陷深度的导体进行分类。对条形和圆形两类缺陷进行的全样本实验和部分样本实验均表明，在导体的近表面缺陷和较深缺陷，单传感器检测算法与融合算法的缺陷检测误差均在0.02 mm以内，均满足检测需求，对于深度为1 mm～4 mm的亚表面缺陷，单传感器检测算法存在局限性，缺陷误差大于0.3 mm，无法满足检测需求，而本文的融合算法具有最优的检测效果。采用本文融合算法，条形缺陷的全样本实验平均误差在0.11 mm以内，均方差在0.055以内；部分样本实验检测效果略逊于全样本训练实验，平均误差在0.12 mm以内，均方差在0.071以内；圆形缺陷的全样本实验平均误差在0.11 mm以内，均方差在0.079以内；部分样本实验检测效果略逊于全样本训练实验，平均误差在0.13 mm以内，均方差在0.083以内，量化的精确度和稳定性均优于单传感器检测方法和常规D-S证据理论方法。