混合策略改进的哈里斯鹰优化算法及其应用*

展广涵王雨虹刘 昊

(辽宁工程技术大学电气与控制工程学院，辽宁 葫芦岛 125105)

群智能算法中的哈里斯鹰优化算法[1](Harris Hawks Optimization，HHO)是Heidari等人提出的一种新型元启发式算法，具有需调参数少、原理简单易实现等优点[2]，在数值和工程优化[3-4]、图像识别[5-6]、故障诊断[7]、电网优化设计[8]等工程领域得到广泛的应用。但HHO与其他群智能算法相似，存在收敛速度慢、全局探索与局部开发行为平衡性较差和易陷入局部极值空间等问题。

针对HHO算法存在的问题，现有文献进行了相关改进研究。文献[9]提出利用多子群的方形邻域拓扑结构和置换概率来平衡HHO的探索和开发能力，并通过随机数组与其他子群个体进行置换，实验结果表明算法在收敛精度和稳定性方面均有所提高。文献[10]在HHO能量函数中引入能量周期性递减因子均衡算法的全局探索与局部开行为，同时利用牛顿局部增强策略提高算法跳出局部最优的能力，但该算法在收敛精度提升的同时增加了计算成本。文献[11]引入贪婪选择、对立学习等策略，避免算法停滞在次优解和过早收敛的问题，提高了算法的收敛精度和抗停滞能力。文献[12]利用混沌映射初始化种群，同时引入进化种群动力概念增加算法抗停滞能力，结果表明，改进后算法的精度和鲁棒性有所提升，但对于Rosenbrock、Step、Quartic测试函数的求解精度和稳定性却低于HHO算法。

上述改进策略在一定程度上提高了HHO的寻优性能，但算法的求解精度仍有提升空间。鉴于上述分析，提出一种混合策略改进的哈里斯鹰算法(Improved HHO，IHHO)。首先，引入精英混沌反向学习策略完成哈里斯鹰种群初始化，在扩大全局探索空间的同时增加初始种群多样性和精英个体的占比，从而提升算法收敛速度和精度；其次，将动态自适应权重引入线性能量递减策略，利用逃逸能量非线性递减策略表征猎物逃逸能量的变化过程，提升算法全局探索和局部开发的平衡能力；最后，通过拉普拉斯交叉算子策略提升种群中最优和次优个体的适应度值，提高算法的抗停滞能力。通过对十个基准测试函数以及一个实际工程问题进行求解，验证了本文算法的优越性和可行性。

1 哈里斯鹰算法

HHO算法通过模仿哈里斯鹰的群体狩猎行为和突袭围捕策略实现优化算法的全局寻优，其捕猎过程分为全局探索和局部开发两个阶段。

1.1 探索行为

当猎物逃逸能量｜E｜≥1时，算法执行全局探索行为，其表达式如下:

式中:X(t＋1)和X(t)分别为第t＋1和t次迭代时鹰的位置；Xrand(t)为第t次迭代时鹰的随机位置；Xrabbit(t)为当前最优个体位置；X m(t)表示种群中心位置；r和q为[0，1]间的随机数；ub与lb表示搜索空间上下限。

在迭代搜索过程中，算法执行全局探索或局部开发的行为取决于线性递减的猎物能量E值的大小，其表达式为:

式中:T为最大迭代次数；E0∈[0，1]为猎物初始能量值。

1.2 开发行为

当猎物逃逸能量｜E｜＜1时，算法执行局部开发行为。哈里斯鹰根据围捕中的随机数r和猎物能量｜E｜与0.5的大小比较形成四种围捕策略。

策略1:软围捕。当｜E｜≥0.5且r≥0.5时，此时猎物具有充沛的逃逸能量E，鹰群执行软围捕策略，鹰的位置更新公式为:

式中:J表示猎物跳跃能量，取[0，2]之间的随机数。

策略2:硬围捕。当｜E｜＜0.5且r≥0.5时，猎物的逃逸能量E较低，无充足能量逃脱，鹰群执行硬围捕策略，其位置更新公式为:

策略3:快速俯冲式软围捕。当｜E｜≥0.5且r＜0.5时，根据式(5)对其位置进行更新并与当前位置的适应度进行比较，若适应度没有得到改善说明围捕失败，则鹰群基于Levy飞行随机游走，使用式(6)进行位置更新。

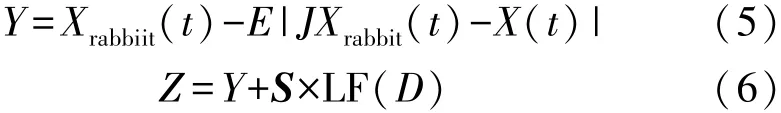
式中:S是维度为D的随机向量，LF为Levy飞行函数。

策略4:快速俯冲式硬围捕。当｜E｜＜0.5且r＜0.5，猎物没有足够的逃逸能力，鹰群执行快速俯冲式硬围捕策略，其位置更新如式(7)所示，若快速俯冲失败则执行Levy飞行随机游走，利用式(6)进行位置更新。

2 改进哈里斯鹰算法(IHHO)

2.1 初始化种群的改进

2.1.1 初始种群多样化

为增加算法初始种群的多样性，利用具有较好遍历均匀性的Tent混沌映射[13]方法初始化哈里斯鹰种群。由于Tent映射存在小周期和不稳定的周期点，因此在Tent映射函数中引入随机变量rand(0，1)×1/N，改进后表达式如下:

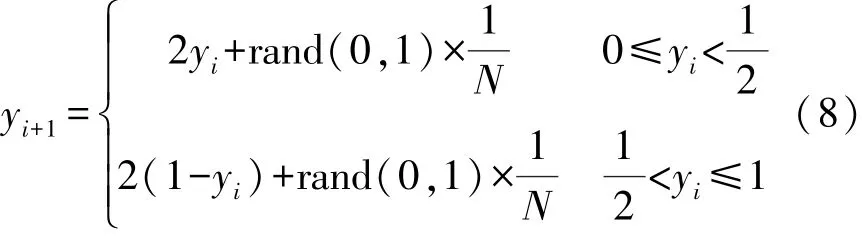
式中:rand(0，1)表示(0，1)之间的随机数；N为Tent序列内粒子个数。

利用式(9)对Tent映射后均匀分布的混沌序列进行逆映射得到种群个体，其表达式如下:

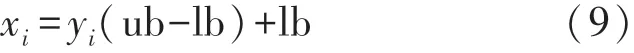
式中:y i为式(8)生成的混沌序列；x i为映射后的哈里斯鹰个体；ub和lb为搜索空间的上下界。

2.1.2 初始种群精英化

根据小孔成像反向学习[14]方法可以增加算法寻优位置的多样性和种群精英个体的数量，帮助算法扩大搜索区域，从而提高选取更优解的概率。假设x j和x′j分别是当前哈里斯鹰最优解和小孔成像后的反向最优解，a j和b j分别为第j维解的上下限，根据小孔成像原理可得:

式中:n为小孔成像调节因子。

2.2 逃逸能量递减机制的改进

猎物逃逸能量E是HHO平衡全局探索与局部开发行为的重要参数。HHO中对猎物逃逸能量E的描述是由最大值线性递减至最小值，即探索阶段和开发阶段逃逸能量变化量ΔE相同，这种线性能量递减策略导致算法的探索和发开平衡性较差，且无法准确表征实际情况下鹰与猎物多轮围捕逃逸过程。为此，在HHO能量递减策略中引入动态自适应权重[15]，提高猎物逃逸能量的非线性表达，从而平衡算法的探索和开发行为，表达式如下:

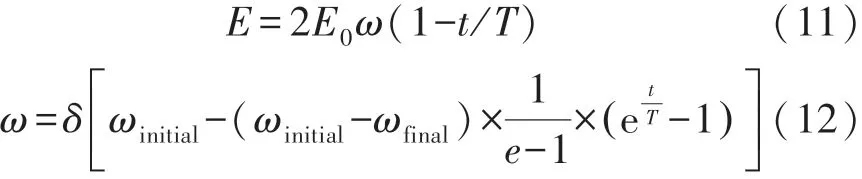
式中:ωinitial为权重初值，ωfinal为权重终值；t为当前迭代次数；δ为[0，1]之间的随机数；T为最大迭代次数。

由图1可知，在迭代初期动态自适应权重能够保持相对较大的值，因此猎物逃逸能量值E较大，从而保证迭代前期算法的全局探索能力。在迭代后期动态自适应权重能够长时间保持在较小值范围，保证算法进行精细搜索的同时延长算法的局部搜索时间，从而平衡算法全局探索和局部开发的能力，改进前后的逃逸能量值E的变化如图2所示。

图1 自适应权重曲线

图2 逃逸能量值E变化曲线

2.3 拉普拉斯交叉算子策略

HHO算法在迭代后期种群多样性降低且对最优个体依赖性较大，当最优个体陷入局部最优后种群难以跳出局部极值空间。为此，采用拉普拉斯交叉算子[16]策略对迭代后期种群内部适应度最高的两个个体进行交叉扰动，然后对比交叉前后个体的适应度值，选择适应度值较高的个体进行下一次迭代。拉普拉斯密度函数和交叉计算公式如下:

式中:U1i和U2i为拉普拉斯算子交叉后产生的子代个体的位置；a∈R为位置参数；b为尺度参数；x1i和x2i分别为解空间中适应度最高的两个个体的位置；β为分布随机数。

图3为拉普拉斯密度函数曲线，可以看出，不同尺度参数b对应不同的密度曲线，根据HHO算法开发阶段在不同围捕策略下鹰群的搜索步长与范围和拉普拉斯密度函数曲线的特性，不同围捕策略下b的取值可分为如下两种情况。

图3 拉普拉斯密度函数曲线

①软围捕策略。当｜E｜≥0.5时，选取b＝1。此阶段猎物逃逸能量值较大，哈里斯鹰群体在猎物上空较大范围盘旋，b＝1时拉普拉斯算子分布密度函数具有更宽的分布范围，使执行软围捕策略的哈里斯鹰个体能够以较大步长探索求解空间，从而跳出局部极值的约束。

②硬围捕策略。当｜E｜＜0.5时，选取b＝0.5。此阶段猎物逃逸能量值较小，哈里斯鹰群体在较小的范围内对猎物进行硬围捕，b＝0.5时密度函数在中心值附近产生随机数的概率较高，使执行硬围捕策略的哈里斯鹰个体能够以较小的步长精细搜索最优区域，提高寻找全局最优解的概率。

2.4 改进算法的逻辑流程

Step 1:初始化参数，包括最大迭代次数T、种群个体数N、目标函数的维数D、初始值上下界lb、ub。

Step 2:利用精英混沌反向学习策略初始化种群，随机初始化生成个体数为N的哈里斯鹰种群X＝[x i1，…，x id]，i＝1，…，N，x i d表示第i只鹰在第d维的位置；将种群X代入式(8)，对每一个个体在每一维的位置进行迭代，生成均匀分布的混沌序列Y；将种群X代入式(10)得到小孔成像反向种群Z，根据个体适应度对种群Y和Z进行排序，选择前N个适应度较大的个体组成种群P；将哈里斯鹰种群X和种群P按个体适应度从高到低进行排列，选择前N个个体重新组成初始种群X′。

Step 3:更新E0和J值，根据式(11)计算猎物非线性逃逸能量E，实现全局探索和局部搜索的转换。

Step 4:当｜E｜≥1时，算法执行全局探索过程，利用式(1)更新种群的位置。

Step 5:当｜E｜＜1时，算法执行局部开发过程，为避免算法陷入局部极值空间，利用拉普拉斯交叉算子策略对软围捕和硬围捕情况下种群最优和次优个体的位置信息进行两种更新策略:

①若｜E｜≥0.5且r≥0.5时，算法执行软围捕策略，利用式(3)更新哈里斯鹰的位置；若｜E｜≥0.5且r＜0.5时，执行快速俯冲式软围捕，利用式(5)和式(6)更新哈里斯鹰位置，并采用式(14)、式(15)对两种策略下的解空间进行拉普拉斯算子交叉，更新种群最优位置。

②若｜E｜＜0.5且r≥0.5时，算法执行硬围捕策略，利用式(4)更新哈里斯鹰的位置；若｜E｜＜0.5且r＜0.5时，执行快速俯冲式硬围捕，利用式(7)对哈里斯鹰位置进行更新，并采用式(14)、式(15)对两种策略下的解空间进行拉普拉斯算子交叉，更新种群最优位置。

Step 6:比较整个搜索范围内所有个体的适应度值，不断更新当前全局最优解，判断是否达到最大迭代次数T，若满足条件，则转至步骤7，否则转至步骤2。

Step 7:输出最优适应度和位置Xrabbit。

2.5 改进算法时间复杂度分析

传统HHO算法的计算复杂度主要取决于三个过程:种群初始化、适应度评估和哈里斯鹰的位置更新。假设种群数为N，目标函数维度数为D，最大迭代次数为T，则HHO算法的计算复杂度为:

在IHHO算法中，假设按式(8)生成混沌种群的时间为t1，按式(10)生成反向种群的时间为t2，则哈里斯鹰种群初始化阶段的时间复杂度为:

猎物逃离能量E更新一次的时间为t3，则此阶段的时间复杂度为:

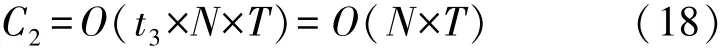
在适应度评估阶段，IHHO算法的计算复杂度与HHO算法的计算复杂度相同；在更新鹰的位置阶段，假设四种围捕策略下采用式(14)、式(15)进行拉普拉斯算子交叉来更新种群最优个体的时间分别为t4、t5、t6、t7，则时间复杂度为:

综上，IHHO算法的时间复杂度为:

因此，IHHO与标准HHO算法的时间复杂度基本相同，对计算机而言改进后的算法所增加计算负担基本可以忽略不计。

3 IHHO算法寻优能力测试与分析

3.1 基准测试函数及实验环境

为验证IHHO的寻优效果和鲁棒性，选取如表1所示的10个典型的单峰、多峰标准测试函数作为实验函数。实验环境为Windows10操作系统，处理器型号为Inter Core i5-10200H，CPU＠2.40 GHz，编程语言为MATLAB2018b。

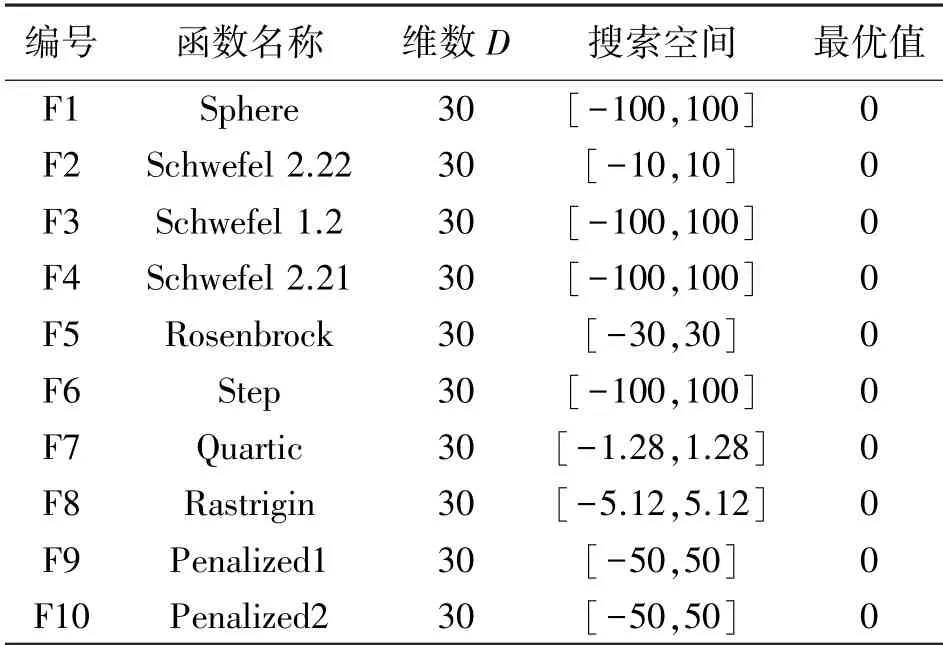
表1 测试函数

3.2 IHHO与其他智能算法的对比

选取灰狼算法(Grey Wolf Optimizer，GWO)[17]、哈里斯鹰算法(HHO)和粒子群算法(Particle Swarm Optimization，PSO)[18]与IHHO算法进行寻优效果对比，问题维数D＝30。GWO、PSO和HHO算法的其他参数设置如表2所示。寻优结果如表3所示。

表2 各算法参数

首先，从表3中的最优值来看，IHHO在求解F1、F2、F4时均能寻找到其理论最优值，与其他3个模型对比，收敛精度提升明显。对F3、F5、F6、F10求解时，4个对比算法均未寻找到理论最优值，但IHHO算法寻优结果的精度远高于对比算法。在求解F8时，IIHHO和HHO均求解出理论最优值，表明IHHO和HHO算法在F8函数有较高的寻优精度。对于F7和F9，IHHO和HHO寻优精度接近，但优于其他对比算法几个数量级。通过对最优值的分析可以看出，IHHO具有更高的收敛精度。其次，从平均值来看，IHHO在10个测试函数上均获得最优的平均值，且在F1、F2、F4、F8上的平均值为0，说明IHHO算法具有更好的寻优性能，值得注意的是，对于函数F7和F9，虽然IHHO和HHO对其求解得到的最优值很接近，但平均值却相差1～3个数量级，说明在30次独立运行中，IHHO算法的整体寻优结果优于HHO算法。最后，从标准差的角度看，对于函数F1、F2、F4、F8，IHHO的标准差均为0，对于其他测试函数，IHHO算法的标准差均优于对比算法几个甚至几十个数量级，说明改进算法具有较强的鲁棒性。综上所述，与HHO和其他对比算法相比，改进后的算法在收敛精度、寻优能力和鲁棒性方面均有所提升。

表3所列平列运行时间为4种算法独立运行30次的平均耗时，其中PSO算法在4个算法中计算效率表现最好，IHHO算法虽然在运行时间上不占据优势，但其收敛精度优于其他对比算法十几甚至几十数量级。此外，IHHO的计算效率与HHO相差无几，验证了IHHO与HHO算法时间复杂度的一致性。

表3 不同智能算法的寻优结果

图4绘制出10个测试函数在4种优化算法下的收敛曲线。由图4可知，对于函数F1、F2、F3、F4、F8，IHHO能够在较少迭代次数的情况下达到或者接近测试函数理论最优值，对于多峰函数F8，虽然IHHO和HHO均能收敛到最优值，但IHHO的迭代次数明显少于HHO，表明精英混沌反向学习策略的引入增加了初始种群的多样性与选取更优解的概率，从而提高了算法的收敛速度。此外，随着迭代的不断进行，GWO、HHO和PSO均出现不同程度的停滞，而IHHO的迭代曲线呈阶梯式下降，表明引入拉普拉斯交叉算子策略在对种群中最优和次优个体进行交叉变异，可提高种群个体适应度值，帮助算法跳出局部最优空间，增加了算法全局探索的能力。

图4 10个测试函数的迭代曲线

3.3 不同改进HHO算法对比

为充分验证IHHO的优越性，选取文献[19-21]与IHHO在10个基准测试函数上进行对比，为保证公平性，4个对比算法的通用参数保持一致，种群规模设置为30，，最大迭代次数设置1 000，为减小偶然性误差，每个算法独立运行30次，结果如表4所示。

表4 不同改进HHO算法寻优结果

由表4可知，除函数F3外，IHHO对其他9个测试函数求解的最优值、平均值和标准差均表现最佳，其中对函数F1、F2、F4、F8均能寻找到理论最优值，且平均值和标准差均为0，表明IHHO具有较高的寻优精度和算法鲁棒性。对于F8函数，4个改进算法均能求解出理论最优值，且平均值和标准差也为0，说明4个改进算法在F8函数上均具有优秀的寻优能力和鲁棒性。综上所述，IHHO算法在对10个测试函数求解时，8个测试函数的寻优结果优于对比算法且其中4个寻找到理论最优解，1个测试函数的寻优结果与对比算法相同，1个测试函数的寻优效果排名第二，验证了改进算法的优越性。

3.4 改进策略的有效性分析

为进一步验证3种改进策略的有效性，利用表1中的测试函数对标准HHO、仅采用精英混沌反向学习策略的HHO(ECHHO)、仅采用动态自适应权重的HHO(DAWHHO)、仅采用拉普拉斯交叉算子的HHO(LCHHO)和IHHO等算法分别在10、30和100维的条件下进行测试。考虑篇幅因素，从表1中选取3个单峰函数和2个多峰函数进行测试。各算法的参数设置与HHO保持一致，各算法独立运行30次后的结果如表5所示。

表5 不同维度下不同改进策略的寻优结果

由表5可知，从最优值和平均值看，在3个维度下IHHO求解F1、F4时均能寻找到理论最优值，ECHHO和LCHHO虽然未寻找到理论最优值，但它们的收敛精度优于HHO十个数量级以上。对于函数F5，在10维度下ECHHO求解结果的精度最优，在30和100维度下ECHHO和IHHO的寻优精度处于同一数量级且优于对比模型，说明引入精英混沌方向学习策略增加初始种群多样性和种群中精英个体数量，提高了算法的收敛精度。对于F9和F10，IHHO和LCHHO的寻优精度相对较高，说明引入拉普拉斯交叉算子策略可以增加算法在多峰函数上的寻优能力，提高算法的抗停滞和全局探索能力。其次，从标准差看，对5个测试函数求解时，IHHO、ECHHO、DAWHHO和LCHHO的标准差均小于HHO，其中IHHO在求解F1、F4时的标准差均为0，说明每种改进策略对算法的稳定性均有不同程度的提高。然而，单一改进策略下HHO算法在不同测试函数上的寻优效果不够稳定，对部分测试函数求解精度提升有限，说明仅引入单一改进策略不能满足算法较高寻优精度和较强鲁棒性的要求，而融合三种改进策略的IHHO在不同测试函数以及不同维度下寻优精度和鲁棒性的提升较为明显。

3.5 IHHO种群多样性分析

为验证改进策略对种群多样性以及改进后的算法在迭代时收敛性的影响，利用Sphere测试函数进寻优实验，问题维度D＝3。IHHO初始化后的种群分布如图5(a)所示，绘制IHHO迭代10、50次后哈里斯鹰个体位置分布图，同时与HHO迭代50次后种群个体位置进行对比，图中五角星标记表示全局最优值，图形标记表示哈里斯鹰个体，种初始群数设置为50。

从图5中可以看出，利用精英混沌反向学习策略对哈里斯鹰种群进行初始化后，哈里斯鹰个体均匀地分布在最优值附近，避免了HHO算法采取随机分布初始种群造成的种群多样性少且分布不均的问题。通过图5(b)、5(c)、5(d)可知，IHHO随着迭代的进行哈里斯鹰个体以较快的速度向最优值聚集，且迭代后的种群个体分布仍能保持较好的均匀性，对比图5(d)和(e)可以看出，IHHO迭代50次后种群个体仍均匀分布在全局最优值附近，而HHO种群中心明显偏离全局最优值，说明改进策略有效提升了初始种群的多样性以及迭代过程中的收敛性。

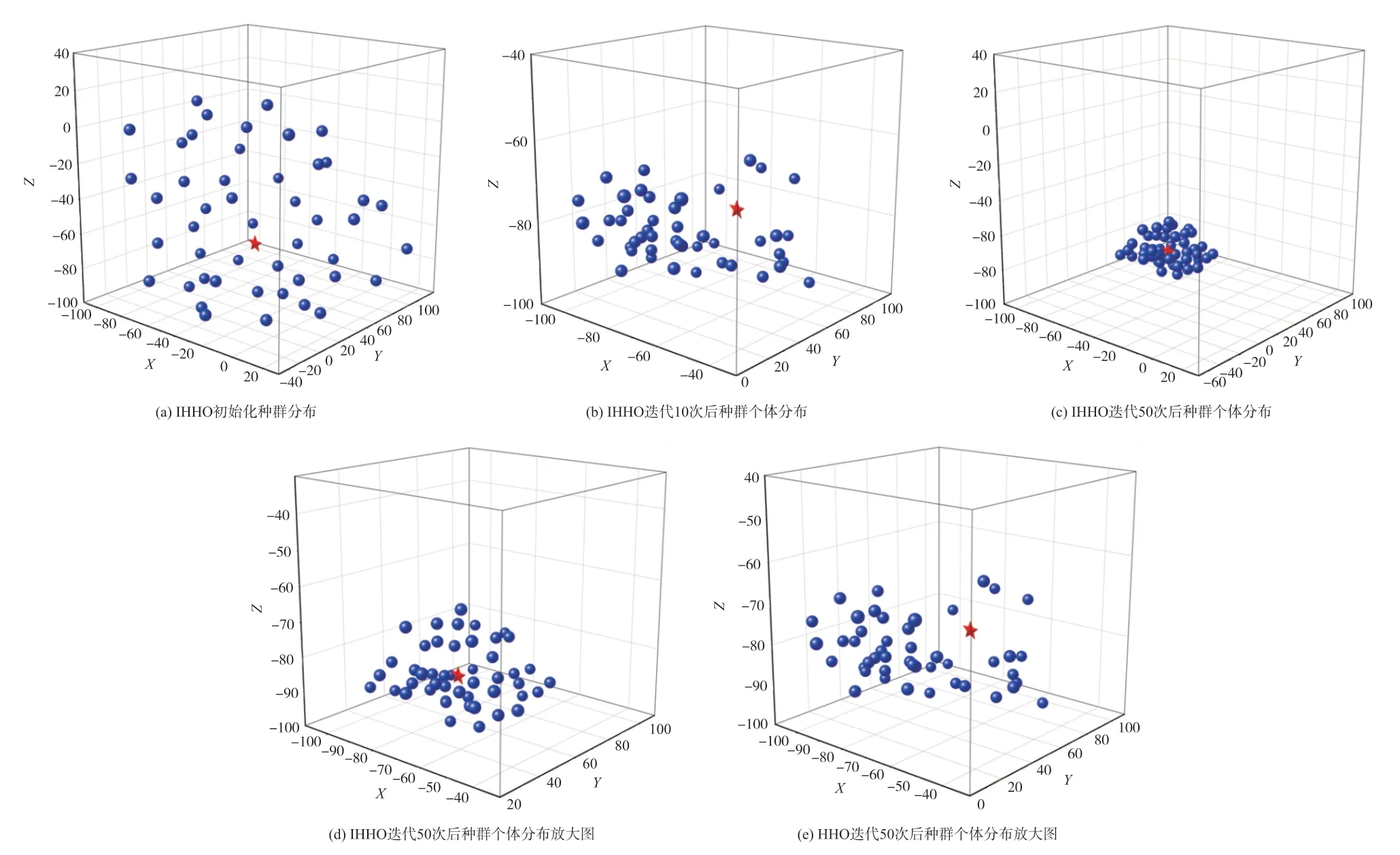
图5 IHHO和HHO种群分布图

4 LSTM优化对比实验

为了对改进算法进行有效性验证，选择深度学习神经网络长短时记忆[22](Long Short Term Memory，LSTM)作为优化对比实验的模型。由于深度学习模型超参数的设定对预测精度影响很大，如果采用随机或根据经验的方式设定模型超参数，无法满足模型最佳参数值和预测精度的要求，因此改进优化算法主要是用于对模型超参数进行寻优，以期能够寻找到最佳的超参数值，从而提高模型的预测精度。另外，对于深度学习模型来说，输入数据的长度以及维度对模型预测精度也存在较大影响，因此，将利用红外测距传感器和气体传感器等不同类型的传感器采集的多组瓦斯涌出量影响因素数据作为特征量输入预测模型。由于不同类型和放置位置的传感器采集的数据量纲不同，因此需要对其进行归一化处理后，作为LSTM模型的输入。

本文选取HHO、GWO、PSO和IHHO算法分别对LSTM的隐藏层神经元个数和学习率两个参数进行寻优，并利用优化得到的不同模型对瓦斯涌出量相关数据进行仿真实验，从而验证算法寻优的效果。

4.1 实验数据选择

实验数据采用山西某矿井工作面历史监测数据，共计1 000组实测数据作为研究对象，其中训练集与测试集的划分比例为4∶1。瓦斯涌出量的影响因素众多，结合矿区的实际情况，选择包括煤层瓦斯含量X1(m3/t)、煤层深度X2(m)、煤层厚度X3(m)、采高X4(m)、采出率X5、开采强度X6(t/d)共6个因素[23]，绝对瓦斯涌出量为Y(m3/min)，瓦斯涌出量影响因素部分监测数据如表6所示。

表6 瓦斯涌出量相关影响因素部分监测数据

4.2 仿真结果与分析

分别利用 IHHO-LSTM、GWO-LSTM、PSOLSTM、HHO-LSTM、LSTM等预测模型对瓦斯浓度进行预测，各模型预测结果如图6所示，4种预测模型的误差对比如表7所示，选用平均绝对百分误差eMAPE、均方根误差eRMSE和平均绝对误差eMAE对模型的预测精度进行评估，其表达式为:

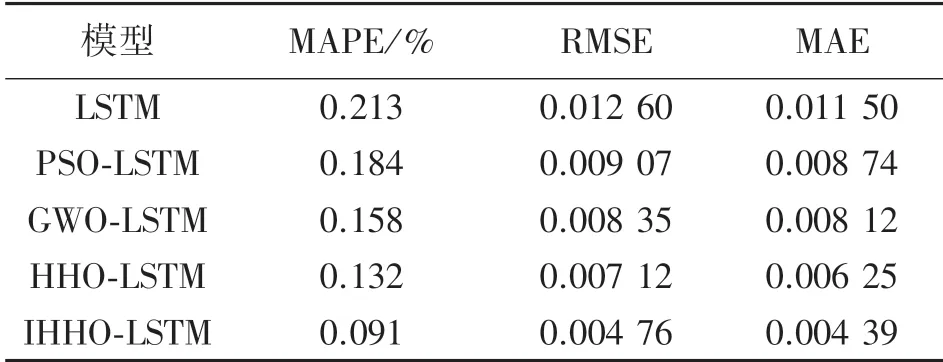
表7 不同模型预测误差

图6 不同模型预测结果

式中:、y i分别为预测值和实际值；n为样本容量。

对比图6中不同模型的预测曲线可知，IHHOLSTM模型的预测结果与实际值的拟合度最高，其在波峰、波谷、拐点和极值处与实际值曲线的贴合程度均优于其他对比模型。根据表7中的数据，与4个对比模型中预测精度最高的HHO-LSTM相比，IHHOLSTM模型的的三个评价指标MAPE、RMSE、MAE分别下降了31.57%、33.14%、29.76%。由上述分析可以看出，IHHO优化后LSTM的预测精度最高，表明IHHO算法相比于其他算法对LSTM参数的优化效果更好，验证了IHHO算法优秀的寻优能力。

5 结论与展望

为改善HHO的寻优性能，利用精英混沌反向学习、引入动态自适应权重的非线性逃逸能量递减机制、拉普拉斯交叉算子三个策略对哈里斯鹰算法进行改进，并利用10个测试函数对其进行测试，验证了IHHO算法收敛性、鲁棒性以及跳出局部最优空间能力的优越性。此外，为验证改进策略对种群初始化以及迭代收敛性能的影响，分别绘制算法改进前后种群初始化以及迭代过程种群分布图，结果显示改进后的种群在初始化和迭代过程中的分布均匀性与收敛性均有所提高。最后，将经过IHHO优化后的LSTM模型应用于瓦斯涌出量预测，并与不同算法优化后的LSTM模型进行对比，其中，与HHO-LSTM相比三个评价指标分别降低了31.57%、33.14%、29.76%，进一步验证了改进算法的优越性。近年来，传感器网络技术在电机故障诊断领域得到广泛的关注，但现有的研究通过传感器网络直接将所有原始数据上传至上位机，造成数据传输难度以及节点能耗的增加。因此，下一阶段的工作将拓展IHHO算法在传感器网络电机故障诊断领域的应用，利用算法直接在传感器网络节点上进行数据处理，以期减少数据在传感器网络中的传输量和传递时间，并减少节点损耗。