基于DTW的多状态负荷的非侵入式负荷分解

裘星，尹仕红，张之涵，潘深琛，江敏丰，杨建明，郑建勇

（1.中国南方电网 深圳供电局有限公司，广东 深圳 440304；2.东南大学 电气工程学院，南京 210096）

0 引言

随着传感技术、测量及存储技术的进步，居民用电数据的监测和采集变得相对便捷，为非侵入式负荷监测（nonintrusive load monitoring，NILM）提供了重要的硬件支撑条件，近年来人工智能算法的提出为非侵入负荷分解提供了解决思路［1—2］。传统的侵入式负荷监测需要在居民用户的每个用电设备上安装测量设备，尽管可以获取每个用电设备的精确数据，但是存储的数据量过大且需要在每一个用电设备上加装测量及存储设备，对于数据的存储和处理以及设备成本问题都是实现负荷监测的瓶颈［3—4］。NILM是20世纪80年代由Hurt提出的，其主要策略是通过监测用户入户的总线出的负荷数据，实现不同用电设备的负荷监测与分解［5］。

近年来，国内外对非侵入式负荷辨识算法做了大量研究工作，神经网络以及深度学习为NILM问题提供了新的解决思路。文献［6］采用基于稳态特征的模糊聚类分析（fuzzy c-means，FCM）的算法，在大功率负载以及在单一负荷运行下有较高的识别率，但当存在小功率负荷以及多状态负荷时识别效率不高。文献［7］采用负荷V-I曲线作为负荷特征，并采用卷积神经网络把负荷的V-I特征作为图形参数输入到卷积神经网络（convolutional netural network，CNN）进行训练，得到较好的识别效果，但是V-I特征属于暂态特征，数据量相对较大。文献［8］提出了一种基于动态时间规整支持向量机的非侵入式负荷监测方法，该方法将负荷投切过程中功率波形的变化情况作为负荷辨识的特征，然后采用DTW对波形进行规整，并采用支持向量机算法进行分类，该方法对于功率相近的负荷有较好的辨识效果。文献［9］针对采样频率低的情况设计了针对性的负荷辨识算法，首先识别出负荷中处于常开状态下的负荷，然后将总负荷减去该负荷，得到处于非常开状态下的总负荷，最后进行分解计算，能够得到低采样频率下较高的识别效果［10—11］。

上述方法需要采集用户用电负荷的暂态信息，因此对于硬件设备的要求较高不宜推广使用。本文采用滑动时间窗的事件探测算法，提出一种基于稳态特征和动态时间规整（dynamic time warping，DTW）的多状态非侵入式负荷分解模型，并利用某年美国波士顿居民用户用电数据集REDD（reference energy disaggregation dataset）进行模型的训练和测试，并对比单一负荷特征下的DTW识别算法，验证本文所提的非侵入式负荷识别算法的优越性［12］。

1 居民负荷稳态特征研究

相比于暂态特征，稳态特征记录的数据集对于硬件的要求较低，但是与之对应的特征信息较少，例如谐波、电压与电流的相位角等特征无法被系统采集［13］。在稳态特征中，又分为单状态负荷和多状态负荷。

1.1 单状态负荷

通过对不同单状态电器的开启过程中的波形特征进行可视化研究，可以对不同电器的波形特征进行聚类分析，探索单状态电器与波形特征之间的对应关系［14—15］。

通过对大量电器启动过程进行研究，发现不同电器在开启过程中其功率的波形会呈现不同的轨迹。其开启过程中的功率波形大致可以分为3类，如图1所示。

观察图1发现：A类电器在开启后功率会逐渐上升然后趋于平稳，含有这种启动波形的单状态负荷特征电器有烤炉、电灯等；B类电器在开启后功率会骤然上升后开始下降并趋于稳定，具有该波形特点的电器有冰箱、干衣机等；C类电器在开启后功率会先呈现上升然后下降，然后再次上升的过程，具有该启动特点的电器有微波炉等［16］。

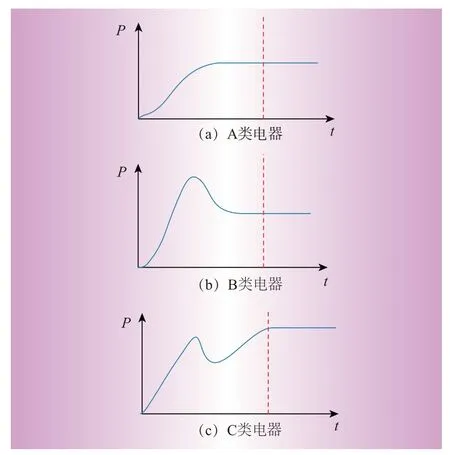
图1 不同电器功率开启波形Fig.1 Power-on waveforms of different electrical appliances

1.2 多状态负荷

相较于单状态负荷，多状态负荷电器为了满足不同的用户需求，往往有多个工作状态，每个工作状态下电器会呈现不同的负荷特性，如功率的波形、幅值、运行的时长等会呈现不同的差异，具有较明显辨识特性。

通常多状态负荷电器中含有变频器作为电机驱动器的电器，如空调、电冰箱、洗碗机等，启动时功率不会即刻上升到额定值，因为采用变频器驱动的电器功率会随着变频器的控制而变化。通过可视化的研究发现，多状态电器每个不同状态下的波形特性与单状态负荷类似，也呈现3种不同开启特性。对多状态负荷的辨识可视为多种单状态负荷辨识的综合［17］。

2 非侵入式负荷识别

本文所采用的非侵入式负荷分解流程如图2所示。

图2 非侵入式负荷分解流程Fig.2 Flow of non-intrusive load decomposition

其中图2左半部分为负荷识别分类器的训练过程，右半部分为分类器实时识别的过程。在分类器实时识别过程中判别负荷类型（是否为多状态负荷）的过程总结为：首先运用DTW算法优先匹配计算波形负荷特征库中单状态负荷波形，并得出DTW计算结果的最小值；然后再次利用滑动时间窗算法提取当前波形相邻的一个波形特征并结合当前负荷特组成包含两个事件特征的负荷波形；最后利用DTW算法匹配计算多状态负荷特征库中的波形型得出最终的分类结果［18］。

2.1 多状态负荷

本文采用滑动时间窗算法用于事件监测，其监测过程如图3所示，滑动窗口分为两个部分，每个子窗口的长度为N，总长度为2N。当有电器投入运行或者有电器切除运行时，总负荷功率会呈现一定的变化，运用该算法监测总负荷功率的波动作并判断事件的起始点和结束点［19］。

图3 基于滑动时间窗的特征提取示意图Fig.3 Schematic diagram of feature extraction based on sliding time window

事件过程起点检测计算如下

事件过程结束点检测计算如下

式中：为起点检查窗口end左半部分的功率平均值；δ2为该部分的功率方差；δ′2为终点检查窗口end右半部分功率方差。当δ′2＜θ·δ2时，认为有暂态事件结束。窗口采点从2N处开始向前滑动检测，当|Pi-＞δ2|时，检测点i认为就是该过程终点。

2.2 动态事件规整

DTW算法是一种恒量两个不同长度的时间序列的相似度的方法，它用满足一定条件的事件规整函数W(n)描述测试模板和参考模板的事件对应关系，求解模板匹配时累计距离最小所对应的整数函数。

假设我们有两个有功功率波形序列Q和C，他们 的 长 度 分 别 为m和n，Q={q1,q2,…,qm}，C={c1,c2,…,cn}。当m=n时，代表两个功率波形长度相同则可直接两个波形之间的距离；当m≠n时，其距离计算过程可参照图4所示。

图4 DTW算法示意图Fig.4 Schematic diagram of DTW algorithm

首先根据波形序列Q和C的长度建立一个m×n的矩阵，在该矩阵中寻找出一条最优路径，路径通过的格点即为两个序列进行计算的对齐的点。定义该路径为W=w1,w2,…,wk,…,wK，其中max(m,n)≤K＜m+n-1。路径的选取遵循的条件：路径必须从左下角出发，在右上角结束；路径上的点不能跨过某个点去匹配，这样保证Q和C上的每个点都出现在矩阵中；矩阵上的点必须是单调递增的，保证中的路径不会出现相交的现象。Q和C中每一点之间的距离如下所示

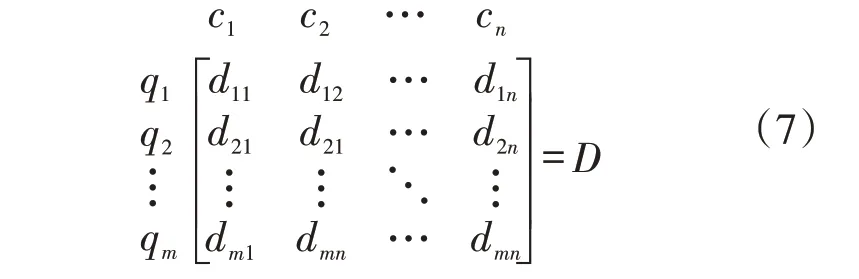
遵循上述条件后，规整代价最小的路径为

通过上述方法可计算与当前波形最佳匹配的功率波形。

3 算例分析

本文所采用的数据集为REDD公共数据集，该数据集记录了某年美国波士顿6个家庭的家庭用电数据，该数据集分为两个主要部分：第一部分为低频采样数据集，该部分数据记录了6个家庭的全部数据，其中每个家庭用户数据包含总线负荷数据和各个支路电器的负荷数据，总线负荷数据的采样频率为1 Hz，各支路电器采样频率为1/3 Hz，且每个记录的功率数据都有对应的时间戳；第二部分数据为高频数据集，该部分数据记录了3号和5号家庭的负荷数据，数据集中包含了电压、电流、循环周期数、时间戳等信息。本文采用低频数据集部分作为研究对象，该部分数据集记录的时间信息如表1所示。

表1 REDD低频部分数据采集时间Table 1 Data acquisition time of the low-frequency part of REDD

表1中测量开始时间指的是4月18日，测量结束时间指的是5月24日。

3.1 数据标定

在对数据集中提取的特征进行训练和测试时，首先必须知道该部分特征所对应的负荷类型，才能进行特征训练和测试结果的验证，但是在REDD数据集中，总线负荷部分并没有标明不同时刻所对应的负荷类型，因此首先需要对总线数据集的负荷进行数据标定。

数据标定的遵循的原则是：电能的传播速度等于光的传播速度，因此各个不同用电设别的启停时刻对应总线负荷中负荷变化时刻相同；总用电负荷的负荷特性与各电器的负荷特性的累计特性是一致的。因此对于总线负荷的数据标定可以整理为

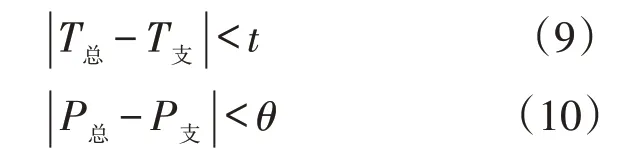
式中：T总、T支分别为总线负荷的记录的时间和之路负荷记录的时间；T总、T支分别为总线负荷功率和之路负荷功率。由于总线负荷记录的频率（1 Hz）与支路负荷记录的频率（1/3 Hz）不同，t为记录不同频率下记录的时间差；θ为总线功率与各支路功率的记录误差，本文设置为40 W。选取用户1作为研究对象，根据标定原则，利用Matlab进行数据的批量处理，并进行可视化分析，结果如图5所示。

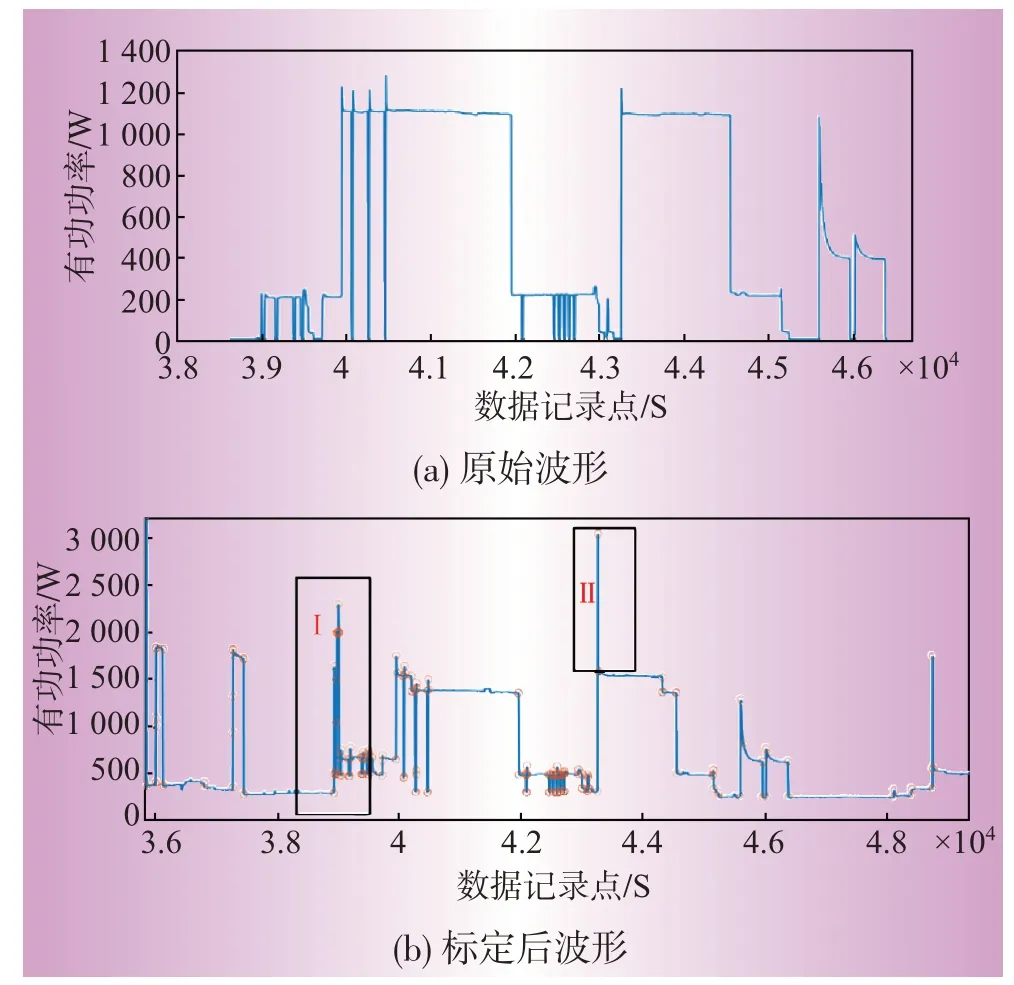
图5数据标定结果Fig.5 Data calibration result

图5(a)为用户1中电器洗碗机的部分功率波形，图5(b)为用户1中总线功率中标定出洗碗机的功率部分。图5中红色圆圈标出的部分为该电器开启或关闭瞬间的时刻，且图5(b)中区域Ⅰ为除洗碗机外有其他电器投切，区域Ⅱ相较于图5(a)有所差异是因为总线的采集频率（1 Hz）与各分电器的采集频率（1/3 Hz）不同导致。

3.2 负荷特征提取及辨识

由于该数据集记录的时间较长，本文选取用户1的数据作为验证数据，选取前30天监测数据作为训练集，第31—36天记录的数据作为测试集。用户1的功率波形如图6所示。

图6 用户1有功功率波形Fig.6 Active power waveform of house1

每一个用户的数据集中既记录了总的负荷功率数据，又记录了每个电器单独运行时的功率数据，对每个电器单独运行时的功率进行可视化研究，找出不同类型电器的波形特点。

对不同单状态负荷的功率开启波形进行可视化研究，得到不同电器的功率波形如图7所示。

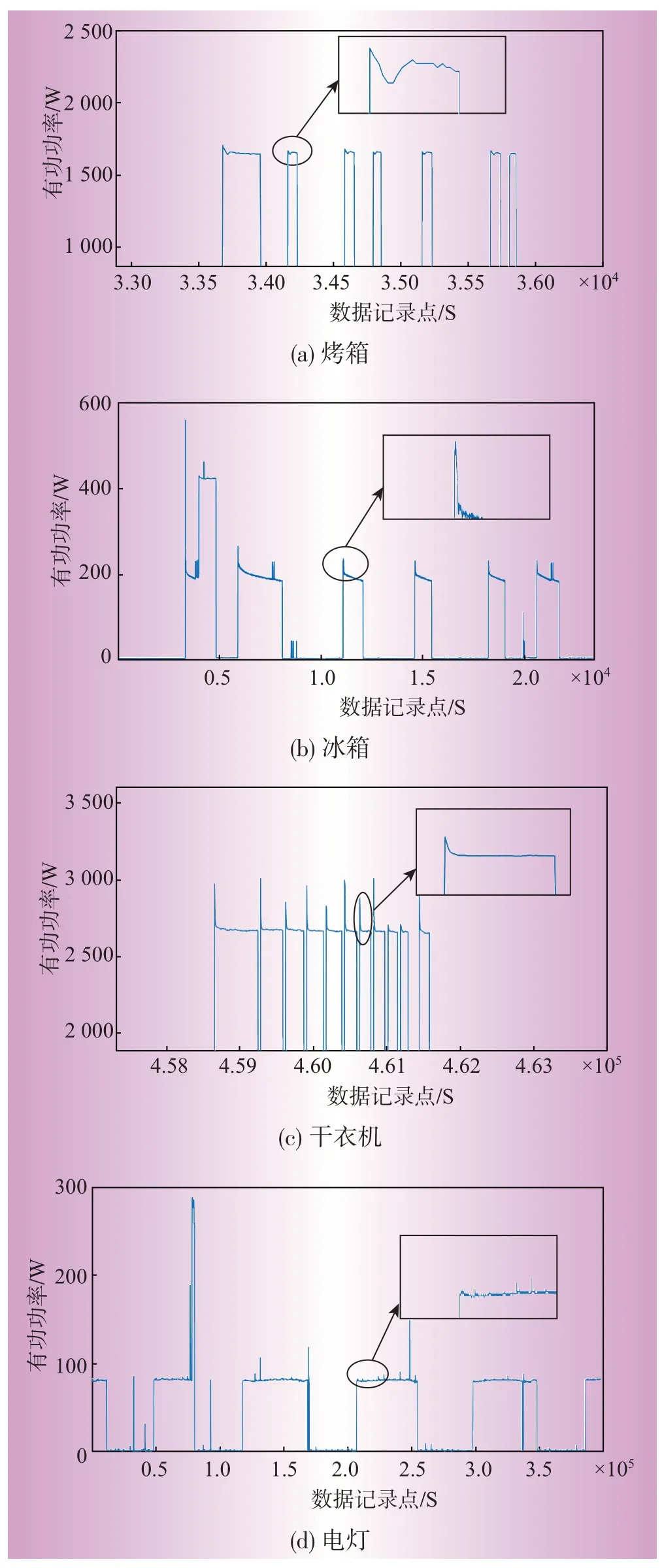
图7 单状态电器稳态波形Fig.7 Steady-state waveforms of single-state electrical appliances

同样对多状态负荷进行可视化研究，并分析多状态负荷的稳态下的功率波形特征，图8为洗碗机的功率波形。

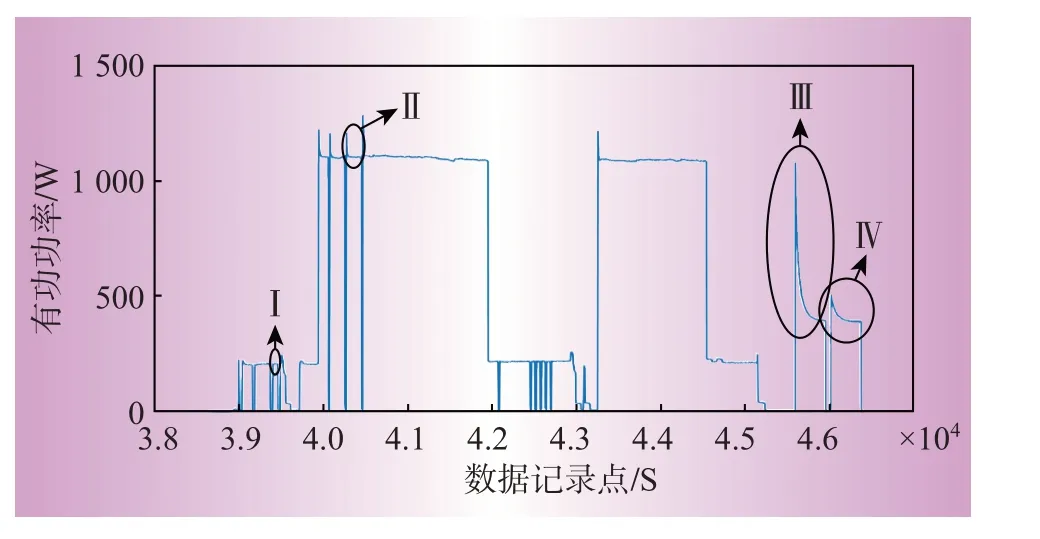
图8 多状态电器稳态波形Fig.8 Steady-state waveforms of multi-state electrical appliances

通过观察多状态负荷波形可知多状态负荷包含多个运行状态，每个运行状态具有不同的波形特征，是区分多状态负荷的重要依据，类似的多状态电器还有洗衣机、空调等。

运用滑动时间窗算法并将功率变化的阈值设置为40，并将提取的功率波形与负荷波形特征库中的波形进行DTW运算得到单状态负荷的匹配情况如图9所示。

图9 单状态电器DTW匹配图Fig.9 DTW matching diagram of single-state electrical appliances

多状态负荷DTW匹配情况如图10所示，从图10可以看出该多状负荷包含两个单状态特征。

图10 多状态电器DTW匹配图Fig.10 DTW matching diagram of multi-state electrical appliances

为了评价该方法的识别效果，本文采用混淆矩阵对识别的结果进行评价，分类结果如表2所示。

表2 混淆矩阵Table 2 Classification matrix

观察表2可知，对于多状态负荷该方法有着与单状态负荷相近的识别效果，证明了该方法的有效性。

3.3 识别效果对比

为了说明本文所提方法的有效性，本文对比了几种常用的负荷识别算法，并采用相同的数据集以及相同的计算平台，其对比识别效果如表3所示。

表3 不同算法识别效果对比Table 3 Comparison of recognition effects of different algorithms

本文采用3种评估指标对识别不同算法进行对比，该评价指标分别为：状态估计准确率、功率分解准确率、计算所用时间。

其中状态估计准确率的计算公式为

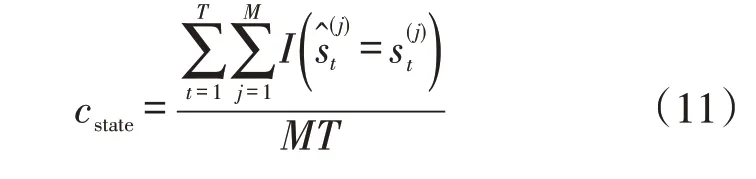
式中：s(tj)为电器j在t时刻状态的估计值为实际值；T为研究时段长度；I(·)为指示函数。状态估计准确率用于评价算法对各个时刻电器工作状态的估计是否准确。

功率分解准确率的计算公式为

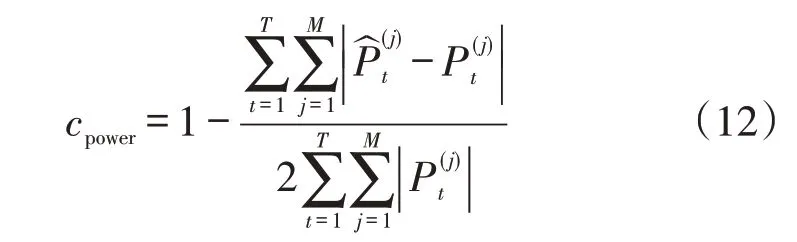
式中：为j电器在t时刻功率的估计值；P(j)

t为实际值。功率分解准确率用于计算各个时刻各电器工作功率的分解结果与实际功率的偏差大小。

计算所用时间为在采用相同数据集和相同平台下，且训练集和测试集的比例相同，其计算所用的时间。

观察表3发现，本文所提方法在对于多状态负荷分解上有着明显的优势，证明了所提方法的有效性。

4 结束语

本文针对稳态特征下的多状态负荷不易识别的问题，提出了一种基于DTW的多状态特征的NILM模型。在多状态负荷识别中，采用包含两个状态下负荷特征作为DTW匹配计算的波形，大幅提升了稳态特征下多状态负荷识别能力。算例结果验证了该模型对于稳态下多状态负荷识别的优越性，对于粒度较高的负荷数据有较好的识别效果且有较好的泛化能力。未来的研究可进一步提升该模型学习能力，能够实时学习并建立负荷波形特征库中没有的负荷特征，提高该模型对于未知负荷的识别能力。D