基于Sine-SSA-BP的永磁直联带式输送系统功耗模型研究

2022-11-21袁志佳朱桂英郭进喜

技术与市场 2022年11期

袁志佳，朱桂英，郭进喜

(河北工程大学机械与装备工程学院，河北邯郸 056038)

0 引言

带式输送机已被广泛应用于煤矿行业。但由于产煤量的不确定性，输送机会出现空载高速、过载等现象，导致其不能高效运行。输送机的运行没有充分利用变频器调速功能，负载大小和驱动功率不匹配，造成了输送机的不必要能源浪费。带式输送系统的节能优化实际上就是优化结构参数、减小运行阻力以及节能运行。由功率的计算公式可知，煤量与带速会直接影响整个系统的能耗。因此，建立永磁直联带式输送系统的功耗模型，找到煤量、带速和功率之间的最优匹配关系，是实现带式输送机节能优化的关键。

对于功耗模型的建立，祝宝君、雷汝海[1-2]分别采用BP神经网络构建了优化模型，减少了输送机的能耗。孙伟等[3]采用BP网络构建模型并用遗传算法对模型参数进行优化，实现了带式输送机的节能运行。目前，针对永磁直联带式输送系统建立功耗模型的研究较少。大多数功耗模型的研究均是针对传统带式输送系统，并且未对所建立的神经网络本身进行优化。

本文采用Sine-SSA-BP算法建立永磁直联带式输送系统的功耗模型。在永磁直联带式输送系统中，已知煤量后，经由优化训练的网络模型，便可找到与煤量匹配的最优带速，达到系统节能的目的。

1 模型建立

1.1 BP神经网络

BP神经网络可映射复杂非线性关系，可以通过训练和学习自动调整参数和结构，并且泛化能力较强[4]。

选取输送机的带速、煤量作为网络模型的输入，对应的网络输出为输送系统的功率消耗。其3层网络结构如图1所示。

图1 BP网络结构图

1.2 麻雀搜索算法(SSA)

麻雀搜索算法(SSA)是2020年提出的新的智能算法，有较好的鲁棒性，寻优速度和能力都有较好的表现。算法通过模拟一部分麻雀发现丰富的食物区域，为其他麻雀提供位置和方向，其他麻雀加入到觅食行为中，当一些麻雀发现捕食者，麻雀规避危险或转移到其他安全的区域进行觅食的行为和规则来实现[5]。

SSA算法中，麻雀个体在运动过程中位置变化可以分为以下3种，在数学上的定义如下。

1.2.1 发现者位置更新

(1)

式中，i：变量，取值为1，2，3，…，n；t：当前迭代次数；N：最大迭代次数；α：0～1的随机数；R2：预警值，取值范围在0～1；ST：安全值，取值在0.5～1；Q：服从正态分布的随机数；L：一个1×d的矩阵，其中L矩阵中各元素均为1。

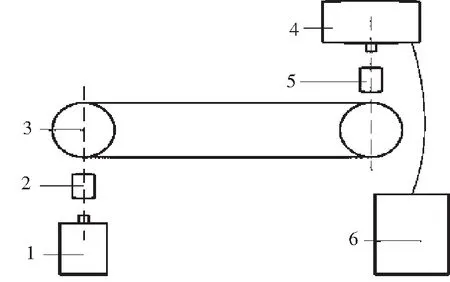
当R2

1.2.2 加入者位置更新

(2)

式中，j：变量，取值为1，2，3，…，n；Xpb：当前发现者的最优位置；Xgw：当前全局最差位置；A：一个1×d的矩阵，其中矩阵中的每个元素为1或-1，并且有A+=AT(AAT)-1。

当j>n/2时，意味着一些适应度值较低的加入者未获得食物。

1.2.3 预警麻雀位置更新

(3)

式中，k：变量，取值为1，2，3，…，n；Xgb：当前全局的最优位置；β：服从标准正态分布的随机数；K：麻雀移动的方向，同时是控制移动距离的参数，为-1～1的一个随机数；fk：当前个体的适应度；fgb：当前全局的最佳适应度；fgw：当前全局的最差适应度；ε：一个较小的常数。

当fk>fgb时，表示麻雀正处于种群的边缘，麻雀感受到危险会躲避风险。当fk=fgb时，处于种群中间位置的麻雀也意识到了危险，此时它们会躲避风险[6]。

1.3 基于Sine-SSA-BP的功耗模型

SSA算法需要通过一种初始化策略来生成初始种群，为后续演化提供初始解。通常，初始种群的选定会影响算法的进程和性能[7]。目前，大多数智能算法均采用伪随机数生成器产生初始种群，而相对于伪随机数生成器，采用混沌数生成器产生的初始种群可以丰富种群多样性，在一定程度上提高算法的性能。因此本文采用Sine混沌映射初始化麻雀种群，选出适应度较好的麻雀个体作为初始种群。

根据BP神经网络的原理，BP神经网络的权值和阈值对所建立的模型会有较大的影响。因此，选用Sine混沌映射优化过的SSA算法对BP网络的权值和阈值进行优化，得到Sine-SSA-BP功耗模型。

首先将功率P、带速v、煤量Q数据集进行归一化处理，并将[P，v，Q]分为训练集和验证集。给定SSA算法的参数：种群数量M、最大迭代次数N、安全阀值ST=0.6、意识到危险的麻雀数量比重SD=0.2、发现者麻雀数量比重PD=0.7。BP网络的输入层为2，输出层为1，隐含层数最优值由算法选出。Sine混沌映射初始化麻雀种群，然后将[P，v，Q]训练集导入到Sine-SSA-BP功耗模型中对模型训练，随着算法的迭代，由式(1)～(3)不断更新麻雀个体的位置。

选用均方误差(MSE)作为算法的适应度函数，算法每循环一次，比较当前麻雀和上一代麻雀最优适应度值大小，若大于上一代值，则更新麻雀位置，否则不更新，最终迭代到满足条件为止，得到全局最优值和最佳适应度。Sine-SSA-BP的流程图如图2所示。

图2 Sine-SSA-BP流程图

2 实例分析

为验证基于Sine-SSA-BP建立的功耗模型的有效性和准确性，本文选用了在永磁直联带式输送系统进行试验所得的数据进行仿真验证。永磁直联带式输送系统的布置示意图如图3所示。

1—永磁电机；2—联轴器；3—皮带机主体；4—负载模拟系统；5—联轴器；6-冷却系统。

由图3可见，永磁直联带式输送系统由永磁电机通过联轴器驱动滚筒，滚筒带动皮带运行，煤量由负载模拟系统模拟。可通过上位机通信变频器控制永磁电机转速。

在永磁直联带式输送系统上，首先给定煤量，煤量由负载模拟系统模拟。然后依据煤量，给定皮带初始经验速度，令系统在—较小功率下运行。通过不断调整负载模拟系统负载和带速，保证煤量不变，直到找到使最小的最优速度，由此得到一组最优的数据。依梯度改变煤量，重复此方法得到242组数据。将数据带入到Sine-SSA-BP功耗模型中进行仿真实验，并选取标准BP神经网络进行对比，得到的仿真结果对比如图4所示。

图4 Sine-SSA-BP与BP仿真结果对比

由图4(a)可见，Sine-SSA-BP功耗模型预测的功率曲线与验证集的实际功率曲线基本吻合，而标准BP神经网络拟合效果相较较差。图4(b)(c)所示，Sine-SSA-BP功耗模型的预测误差和绝对百分比误差更小，即Sine-SSA-BP功耗模型预测更加准确。同时，选取均方根误差(RMSE)进行对比分析，计算结果如表1所示。