装载机铲斗的载荷历程获取及疲劳分析

张继尧，李 冰，徐武彬，张逸彬

（广西科技大学机械与交通工程学院，广西 柳州 545006）

1 引言

装载机铲斗是装载机在工作过程中的直接实施者也是研究的重点，在对装载机铲斗进行研究时，只对铲斗进行静强度的分析是片面的，还必须对其进行疲劳可靠性方面的分析。大多文献的分析均以5T或以上的铲斗进行分析，而对1.2T铲斗的研究较少，1.2T铲斗的结构简单相对耗材较多但装载物料较少，其工作可能存在应力分布不合理以及应力过小的现象，需要对其进行强度及疲劳寿命分析。装载机铲斗在工作过程中所承受的载荷历程是分析铲斗疲劳寿命的基础数据。文献［1-3］通过经验公式法计算的线性变化的载荷历程作为疲劳分析的载荷历程，而在实际的工况中铲斗所受到的载荷多是复杂多变的，采用线性变化的载荷用作铲斗的疲劳分析不符合铲斗工作的实际情况；文献［4-7］借助动力软件结合经验公式来获取载荷历程。由于施加的载荷是通过经验公式计算的，因此与实际情况有一定的差距；文献［8］将离散元分析得到的载荷历程作为疲劳分析的载荷历程，但并未考虑到铲斗本身的惯性及位置与角度变化。结合之前学者的研究，为得到更贴近铲斗实际的疲劳寿命，通过采用多体动力学与散体力学耦合的方式来获得更贴近实际的载荷历程，再利用疲劳计算软件nCode与疲劳理论，对装载机铲斗进行疲劳强度的分析，分析铲斗的疲劳特性，确保其安全工作，为装载机铲斗的可靠性设计提供参考。

2 铲斗载荷历程的获取

2.1 几何模型建立

按照1.2T 装载机的真实尺寸通过Solidworks 建立三维实体模型，由于装载机工作装置的结构比较复杂仅铲斗就有几十个部件，因此需要在保证不影响计算结果的情况下对整个装载机工作装置进行简化。根据ADAMS的计算原理，在不改变质量、惯性矩和部件间连接点位置的情况下对模型进行简化，简化后的模型不会对ADAMS 的计算结果产生影响。将简化后的模型导入ADAMS中。为防止施加约束时使系统具有冗余约束，采用运动副中的移动副、转动副、球副对当前模型施加约束［9］，建立模型。

2.2 材料选择

铲斗是焊合件，采用16Mn 作为材料，其中，屈服极限，σs=345MPa。弹性模量E=（2×106）MPa，泊松比取0.3［2］。

2.3 载荷历程的获取

装载机铲斗在工作过程中可分为五个运动状态：插入物料、转斗、抬升同时平移物料、卸载物料、恢复初始状态。通过在ADAMS中对工作装置的平移及油缸的运动进行设置，对模型进行空载仿真，可以得到铲斗的运动信息包括位移、速度、加速度、角速度，作为下一步离散元仿真的运动设置的基础数据。

由于装载机在工作时受到的载荷是不稳定的，因此只在铲斗处施加恒定或匀变载荷是不符合实际情况的，为实现获取与实际情况较吻合的载荷，使用离散元软件通过散体力学的模拟来获取载荷。选取碎石作为物料，材料属性参数、材料之间接触参数，如表1、表2所示。铲斗的运动信息利用工作装置在ADAMS中空载仿真获得的运动信息，最后仿真获得铲斗的时间-载荷曲线。

表1 碎石与钢的材料属性参数Tab.1 Material Properties of Gravel and Steel

表2 碎石与钢的接触属性参数Tab.2 Contact Properties of Gravel and Steel

将通过离散元软件所得到的时间-载荷曲线加载到ADAMS模型中，加载位置设置在铲斗的下底面质点处，再次进行仿真即可得到铲斗与动臂各连接处的时间-载荷曲线。因为得到的曲线中载荷采用的是不发生改变的整体坐标系，铲斗位置随工作的进程发生改变，而后续的分析中铲斗的位置始终保持不变。因此需要利用铲斗的时间-角度曲线对载荷曲线进行三角函数变换。得到供后续分析的时间-载荷曲线，如图1所示。

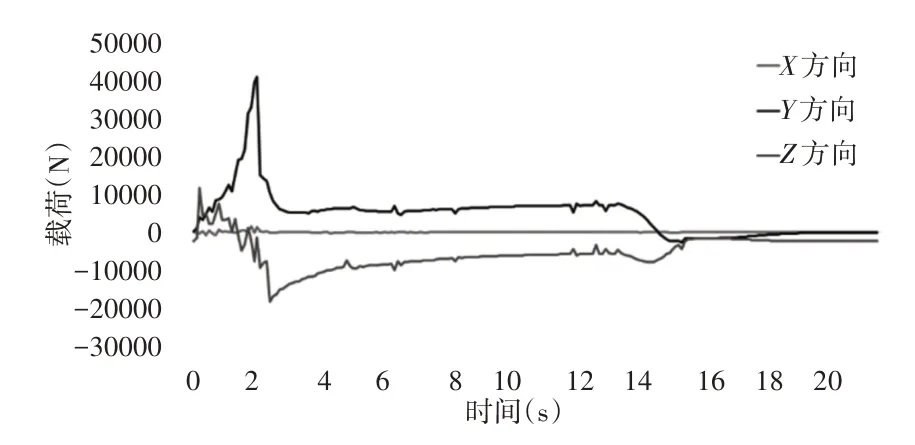
图1 铲斗的时间-载荷曲线Fig.1 Bucket Time-Load Curve

3 静力学分析

分析中装载机行驶的反方向为Y向，垂直于前进方向向上为Z向。

3.1 有限元模型建立

将模型导入Hypermesh软件中，并对模型进行简化，确保简化后的模型不会对分析解结果产生影响。选取3D四面体网格单元，网格尺寸为10，对简化后的模型进行3D网格划分。

3.2 载荷的确定

根据铲斗的时间-载荷曲线，选取所受的纵向载荷最大的时间点2.5s，铲斗正处于插入刚刚开始崛起的状态，该点所对应的横纵载荷分别为8.01kN，15.91kN作为有限元分析的载荷进行分析计算。分析中略去铲斗斗齿，按文献［10］分析的载荷分布对有限元模型施加载荷，装载机行驶方向的载荷作为插入阻力加载到铲斗斗唇，垂直方向的载荷作为崛起载荷均布加载到铲斗下底板。铲斗角耳处三点施加约束，仅保留绕Z向转动的自由度。

3.3 分析结果

通过计算得到铲斗的应力云图与位移云图，如图2、图3所示。

图2 铲斗的应力云图Fig.2 Stress Cloud Diagram of Bucket

图3 铲斗的位移云图Fig.3 Displacement Cloud Diagram of Bucket

2.5 s时铲斗正处于开始崛起料堆的状态，由应力云图可看出铲斗受到的应力主要集中在下侧角耳处，最大应力为130.2MPa，发生在铲斗下侧两个角耳的内侧侧板处，其外侧侧板应力略小为101.7MPa。其余位置应力很小不超过50MPa。铲斗底部结构并不合理，铲斗的底部应力分布不均匀在两个角耳的内外侧均出现应力集中。并且在存在应力集中的情况下，铲斗的最大应力不足铲斗屈服强度的56%，证明改铲斗有很大的优化空间。铲斗出现的最大形变为3.367mm，位于铲斗斗唇中央。

4 实验验证

4.1 实验设计

采用JM3849动态应变测试系统对装载机铲斗进行动态应力应变测试试验。测试环境温度为30°，相对湿度不大于90%，风速不大于4m/s，周围无强烈振动和强磁场干扰。根据铲斗的静力学分析的结果，对应力较大的位置布置应变花，并在实验允许的情况下尽可能多布置［11］。其中仿真产生最大应力的位置在铲斗下侧角耳下侧出，其位于铲斗底部，在实验过程中会因与物料接触而发生破坏，因而选择将应变片布置在下侧角耳的上侧。额外选取铲斗明显特征处补充布置应变花以便参照，共选择14个测点进行测试，本次实验中测点分布，如图4所示。

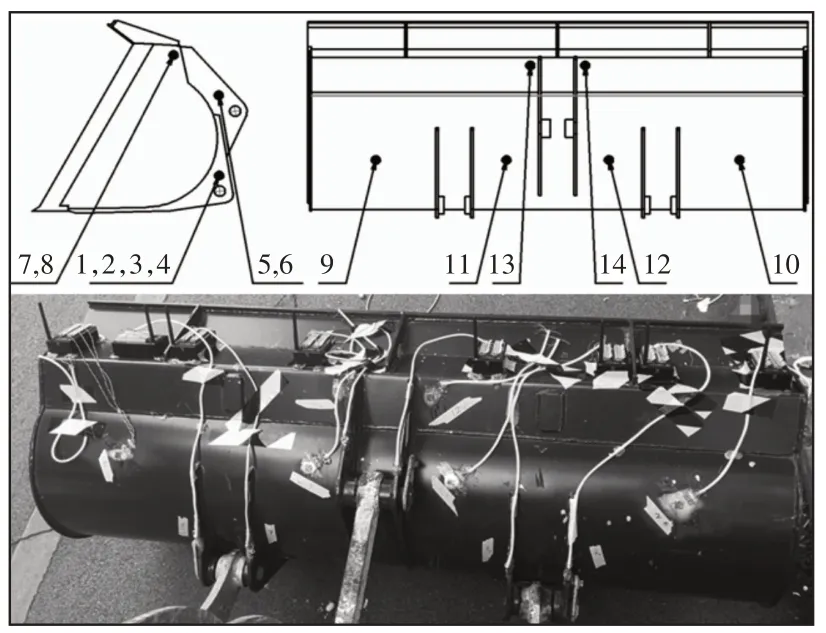
图4 铲斗应力测点布置图Fig.4 Bucket Stress Measuring Point Layout

4.2 实验结果

经过多次实验测试，对实验数据进行了多次计算，得到装载机铲斗在整个工作过程中各个测点的时间-应变的关系。通过对装载机铲斗作业过程进行数据统计，可以获取铲斗0°、45°、90°三个方向上的应变值ε0，ε45，ε90。根据铲斗材料的弹性模量E和泊松比μ，通过式（1）可以计算出测点的最大主应力σ1和最小主应力σ3，从而由第4强度理论式（2）可以得到测点的等效应力σr。

通过计算得到14个测点在整个工作过程中应力随时间的变化曲线，经过对多组实验数据的初步分析与仿真结果相对比，其中测点5-12在实验过程中与有限元分析中均应力很小，使环境等因素的比重增大，因此不做重点讨论。得到时间-等效应力曲线，如图5所示。

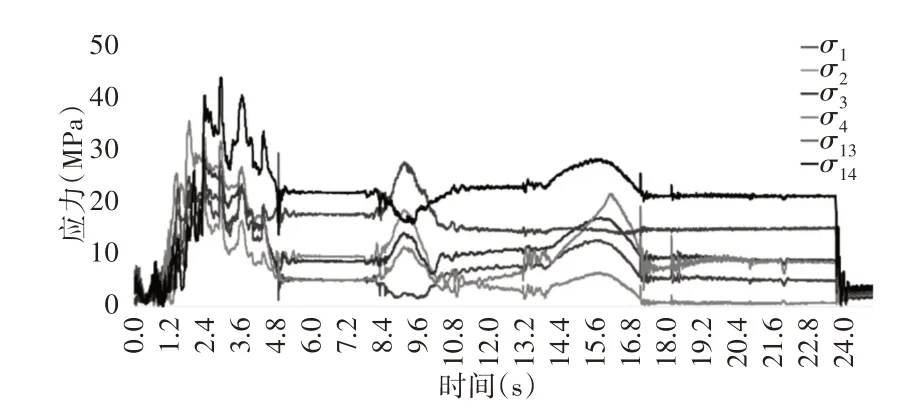
图5 时间-等效应力曲线Fig.5 Time-Equivalent Stress Curve

由于实验中装载机为人工驾驶及受环境限制等因素，装载机的铲装情况与步骤无法与多体动力学仿真过程完全一致。随机选取任意3 个时刻的实验数据中各测点应力，在仿真所得载荷历程中选取对应相似工况的载荷，对有限元模型施加该时刻的载荷并进行有限元分析得到仿真结果，在有限元分析结果中选取最接近测点的一个单元，提取其应力状况用来与试验结果作对比，对所得载荷历程进行验证。实验数据与仿真数据对比，如表3所示。

表3 实验数据与仿真数据对比Tab.3 The ExperImental Data are Compared with the Simulation Analysis

通过与实验数据进行对比，大多数测点的实验值与仿真值的误差在15%以内。有个别测点的误差大于15%，其中第三组的测点2最为明显，由于测点应力过小使得环境等因素的影响显得较为突出的原因。可以认为仿真结果与实验结果在误差15%的范围以内一致，证明采用离散元与多体动力学结合的方法可以获得接近实际情况载荷历程。

5 疲劳寿命分析

5.1 疲劳分析方法

采用nCode软件对铲斗以及动臂的疲劳寿命进行分析，疲劳寿命分析流程，如图6所示。

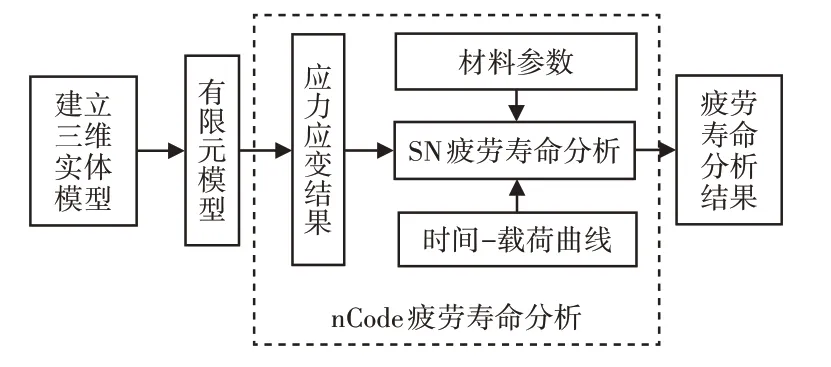
图6 疲劳寿命分析流程图Fig.6 Flow Chart of Fatigue Life Analysis

5.2 线性疲劳损伤累计理论

线性疲劳损伤累计理论认为：材料在循环载荷作用下产生的疲劳是可以累加的，每个应力产生的损伤相互独立、互不干涉，可以进行线性累加。当疲劳损伤累积后达到某一数值时，材料就发生破坏。Plamgren-Miner［12］理论是线性疲劳损伤累计理论中最典型的理论。Miner理论认为，材料的总损伤为D，某一个循环载荷产生的损伤为Di=，则n个循环载荷产生的总损伤为：

式中：Ni—应力水平为Si时的疲劳寿命；ni—水平为Si的应力循环次数。D取到1时材料发生疲劳破坏线性疲劳累计损伤理论显著地简化了疲劳机理，广泛应用于工程实际［13-14］。

5.3 铲斗材料的S-N曲线

一般的S-N曲线是通过材料多次的拉伸疲劳实验获得，而在nCode软件中用输入材料的强度极限、第一截距、第一强度指数、第二强度指数、疲劳转折点、对数标准差、循环特征、杨氏模量，就可以在软件中生成相应的S-N曲线［15］。经过计算，16Mn的S-N曲线，如图7所示。

图7 16Mn的S-N曲线Fig.7 The S-N Curve of 16Mn

5.4 疲劳寿命计算

将静力学分析所得的铲斗与动臂的应力与位移结果导入nCode软件中，将ADAMS的结果通过三角变换所得到的时间载荷历程作为疲劳分析中的载荷历程曲线，分别施加在有限元模型中各载荷工况的分析结果上。根据铲斗结合实际运行工况中的载荷曲线及其受力特点可知，铲斗的破坏形式属于高周疲劳，在疲劳分析中应采用多轴疲劳的分析方法［16］。平均应力修正采用Goodman算法，表面处理采用简单机械加工，多轴应力状态评估采用Standard进行计算，计算结果，如图8所示。

图8 铲斗的疲劳寿命云图Fig.8 Cloud Diagram of Fatigue Life of Bucket

根据寿命云图分析，铲斗在不考虑磨损的情况下最薄弱的地方位于下部角耳内侧，在工作（4.554×105）次，根据每天连续工作5h计算，在连续工作约2年后出现疲劳损伤。

6 结论

（1）通过实验分析验证了采用离散元与多体动力学耦合的方法可以获得更加接近实际情况的装载机铲斗工作中的载荷历程。以此进 行疲劳分析可以获得铲斗更加准确的疲劳寿命。

（2）通过有限元分析，发现1.2T装载机铲斗作业时存在应力集中现象，且应力不足屈服应力的56%，有待结构优化。

（3）在有限元静力学分析的基础上，结合nCode软件利用所得载荷历程对铲斗进行疲劳寿命分析及计算，确定了在实际工作中铲斗下部角耳外侧下部更易发生疲劳损坏，为1.2T铲斗的进一步改进提供依据。同时得到铲斗的实际寿命约为（4.554×105）次铲装。