Quantum routing of few photons using a nonlinear cavity coupled to two chiral waveguides

Jian-Shuang Liu(刘建双), Ya Yang(杨亚), Jing Lu(卢竞), and Lan Zhou(周兰)

Affiliation Synergetic Innovation Center for Quantum Effects and Applications,Key Laboratory for Matter Microstructure and Function of Hunan Province,Key Laboratory of Low-Dimensional Quantum Structures and Quantum Control of Ministry of Education,School of Physics and Electronics,

Hunan Normal University,Changsha 410081,China

We investigate few-photon scattering properties in two one-dimensional waveguides chirally coupled to a nonlinear cavity. The quantum states of scattered few photons are solved analytically via a real-space approach, and the solution indicates the few-photon reflection and transmission properties. When inputting two photons of equal energy to resonate with the cavity,the propagation characteristics of the two photons will be interesting,which is different from the previous anti-bunching effects with a quantum emitter. More importantly,when the total energy of the two incident photons equals the energy of a nonlinear cavity accommodating two photons,influence of the bound state will become larger to result in disappearance of antibunching effect.However,the bound state has no effect on probability of routing to another waveguide.

Keywords: quantum routing,few-photon scattering,nonlinear cavity,chirally couple

1. Introduction

Quantum networks are an important part of quantum information processing and quantum communication, which is composed of quantum channels (to ensure low dissipation of quantum signals transmitted along the channels) and quantum nodes (to control the transmission of quantum signals).Photons become an ideal candidate for carriers of quantum information,[1–10]because they travel fast and are not significantly affected by decoherence effects over long distance.Waveguide can naturally guide photons, so waveguide quantum electrodynamics (QED) is a hot research topic in recent years. One-dimensional (1D) waveguides exhibit diversity as they can modulate the transmission of photonic states by coupling with quantum emitters.[11–15]There are various types of quantum emitters,including quantum dots,[16–18]two-level atoms,[19–25]three-level atoms,[26–28]side optical cavities,[29–31]and cavities with an atom[32–36]or nonlinear Kerr mediums.[37–39]Many physical phenomena have been studied, such as electromagnetically induced transparency(EIT),[40–42]Fano resonance,[43–45]polarization effect,[46]slow light behavior,[47]and multi-photon transport.[48,49]However, these research works mainly focus on the structure of a single 1D waveguide coupled with a two-level system or single-photon qubit.

In recent years, chiral waveguide QED[50,51]has opened up exciting new ways to study interaction between light and matter, which has attracted wide attention. Many quantum systems have realized chiral coupling,[52–58]and it is found that the reflection and transmission of photons in these systems will become asymmetric,and the propagation of photons is irreversible. Therefore,the study of structures composed of multiple one-dimensional chiral waveguides has attracted our attention because of its valuable applications in quantum networks.

In this paper,we investigate the scattering problem of few photons in two one-dimensional waveguides chirally coupled by a nonlinear optical cavity. Note that it is difficult to obtain both strong Kerr nonlinearity and low loss. However,compared with a waveguide coupled atom, intuitively speaking, the atom can at most absorb only one photon at a time,and the optical cavity we study can absorb multiple photons,so it is very interesting to study the transport characteristics of multiple photons. In real space, we give an explicit construction of the exactn-photon scattering eigenstates and then discuss the transport properties. In the analytic expression of amplitude for single photon, we show that in the case of chiral coupling, the reflection and transmission of single photon become asymmetric due to the addition of a waveguide(quantum channel),realizing the non-reciprocity of a single photon.Then,by analyzing the scattering eigenstates of two photons,on account of the possibility of that the nonlinear cavity can absorb two photons at the same time, we discuss two special cases. These show rich characteristics,including the influence of the two-photon bound state, which are valuable for many experiments of multi-photon quantum routing. The rest of the paper is organized as follows.In Section 2,we present the theoretical model of the chiral coupling of a nonlinear cavity to two one-dimensional (1D) waveguides, and give an effective real space Hamiltonian of the system. In Section 3,we use the decomposition of scattering matrix (Smatrix) to greatly simplify the calculation process, and discuss the transport properties of two-photon in detail. Immediately,obtain the output wave function for the photon pair incident from one port of a waveguide,the anti-bunch and bunch effects are discussed for photon-pair appearing to the same port,and the conditions of incident photons routed to desired ports are studied. Finally,we conclude with a brief summary of the results.

2. Model and hamiltonian

where ˆd( ˆd†)is the annihilation(creation)operator of the cavity mode with frequencyΩ,which is far away from the cutoff frequency of the waveguide modes.The second term in Eq.(2)describes the Kerr nonlinear interaction with strengthU. For the sake of simplicity, we first neglect the photon loss in our calculation. For finiteU,an addition energyU ＞0 is required to add a further boson to thedmode once thedmode is occupied by one photon.

Fig.1. Schematic of a few-photon router with four ports: A nonlinear cavity system interacts with two independent waveguides labeled by a and b. The blue (green) line represents the chiral coupling between the nonlinear cavity with Kerr medium U and the left and right going photons of the bottom waveguide a(b),and the coupling rates are γar (γbr)and γal (γbl),respectively.

The chiral coupling between the cavity and the waveguide modes reads

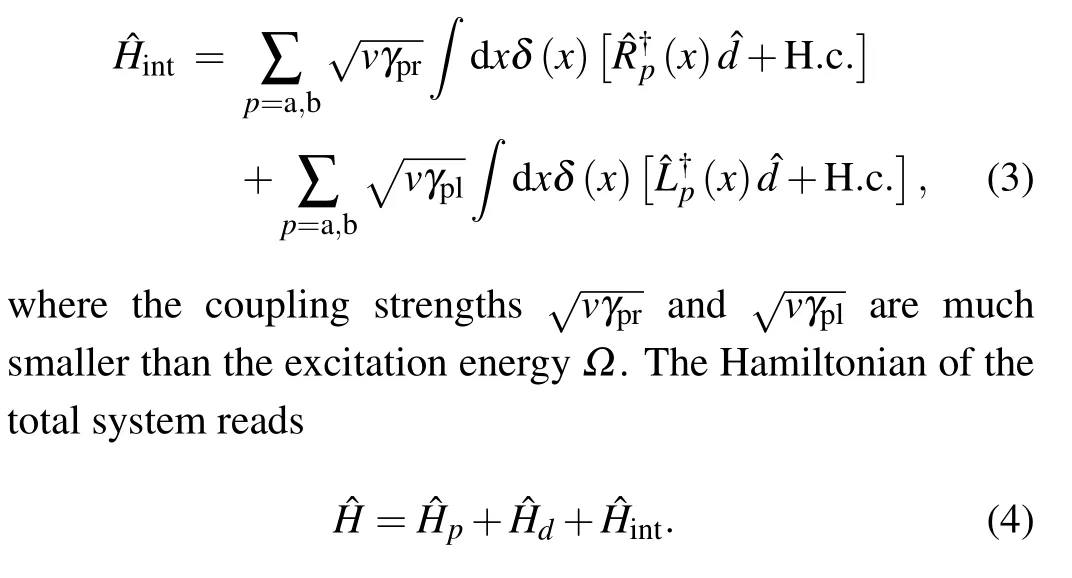
This Hamiltonian describes the case in which a propagating photon can travel in both directions of two one-dimensional waveguides,so that the nonlinear cavity interacts with the four modes.

We employ the following transformations:

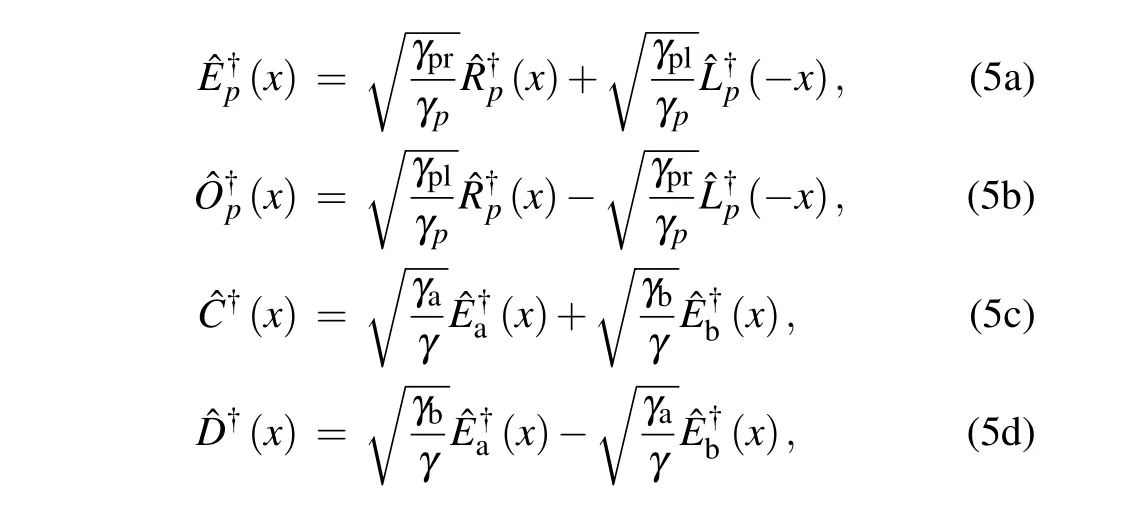
whereγp=γpr+γpl,γ=γa+γb, the original Hamiltonian is transformed into four decoupled “one-mode” Hamiltonians,i.e., ˆH= ˆHC+ ˆHDO,where

BecauseHcommutes with certain number operators,[ ˆH,ˆnC+ˆnd]=[ ˆH,ˆnDO]=0, the total numbers of excitations in both the three-mode and theC-mode spaces are separately conserved. In other words, the three modes evolve freely in the waveguide. Therefore we shall focus on the calculation of the transport properties of the photons inC-mode,and then transform back to the left(right)representation.

3. Scattering in two-photon excitation

Assume that there are two incident photons in the waveguide from the left side with momentakandp, respectively,the frequencyω=v(k+p)and the energy difference between two photonsΔ=v(k-p)/2. Physically, there may be three cases of two photons: (i) Both photons are in waveguideCmode. (ii)One photon is in waveguideC-mode and the other photon is absorbed into nonlinear cavity.(iii)Both photons are absorbed into nonlinear cavity. In the free two-photon Hilbert space, its real-space representation consists of a symmetric function of the coordinates of the photonsx1,x2, and is defined asφCC(x1,x2). The general two-photon scattering state of the system in the spaces withC-mode takes the following form:

We useφCC(0,x)≡(1/2)[φCC(0+,x)+φCC(0-,x)]. The functionsφCC(x1,x2)ande(x)are piecewise continuous. Applying the bosonic symmetrical statistics, we can settle forφCC(x1,x2)by first considering the half-spacex1＜x2and then by interchangingx1⇐⇒x2to extend the result to get the full space. In this case, there are three quadrants in real space:x1＜x2＜0,x1＜0＜x2, and 0＜x1＜x2. In the region that all photons are away from the cavity,the plane wave with wave vectorskandp. We require that the incoming wave functions consist entirely of plane waves,that is,forx1＜x2＜0,

Each of photons impinges on the quantum node, being eventually scattered off. Every one may be reflected (transmitted) to the left (right) side of the quantum node (denoted as port 1 (2)) in waveguidea, or be reflected (transmitted) to the left (right) side of the quantum node (denoted as port 3(4))in waveguideb. Then the output state contains ten terms:Both photons are transmitted to port 2 or 4 with amplitudesρ22(xc,x)andρ44(xc,x),

Fig. 2. Plots of dimensionless quantities: (a) T22, (b) R11, (c) T44, and (d) R33, as a function of two-photon transmission and reflection of waveguides a and b,respectively,k/γ and p/γ,when γar=0.25γ,γal=0.35γ,γbr=γbl=0.2γ at x=0.

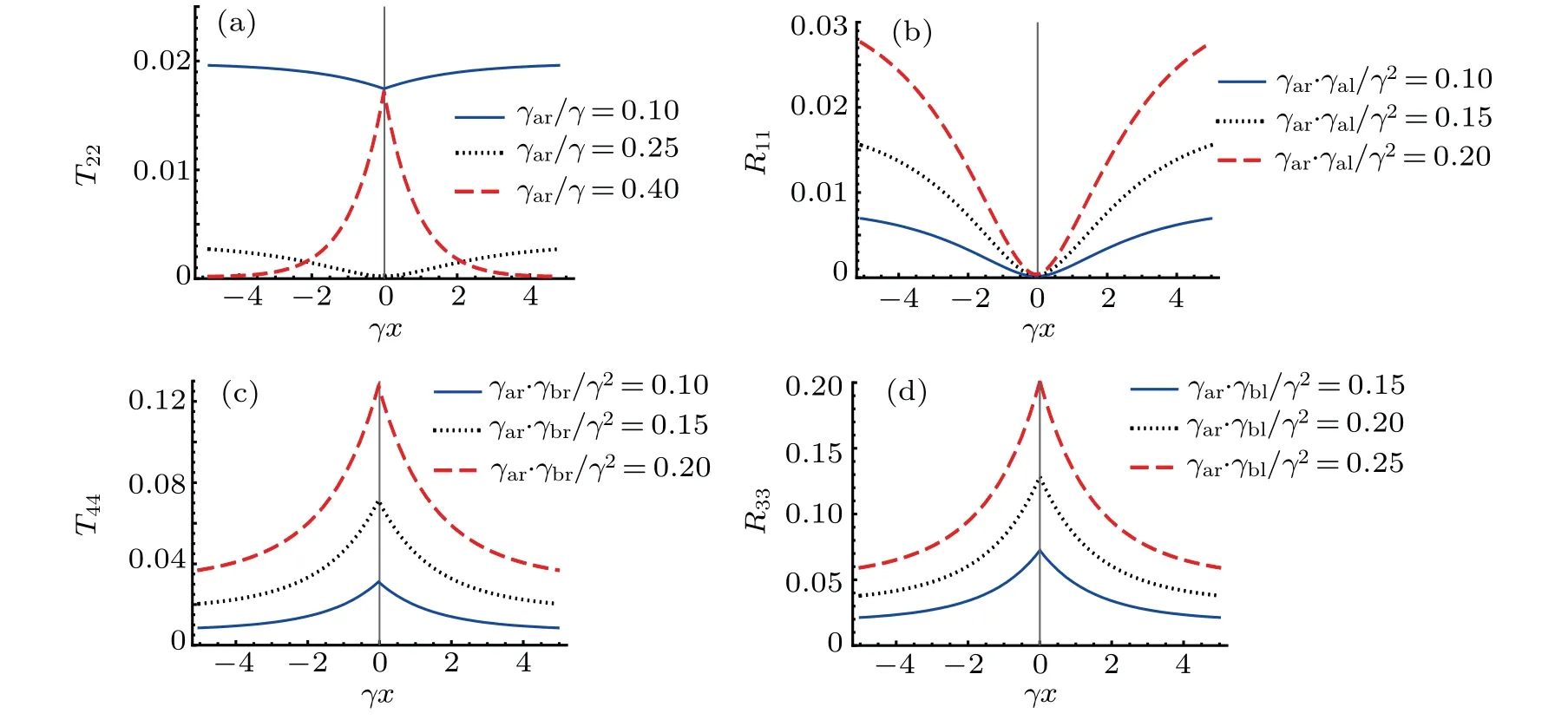
Fig.3. The(a)T22,(b)R11,(c)T44,and(d)R33,as functions of relative coordinate γx. The other parameters are vk=vp=Ω =100γ,U=10γ.

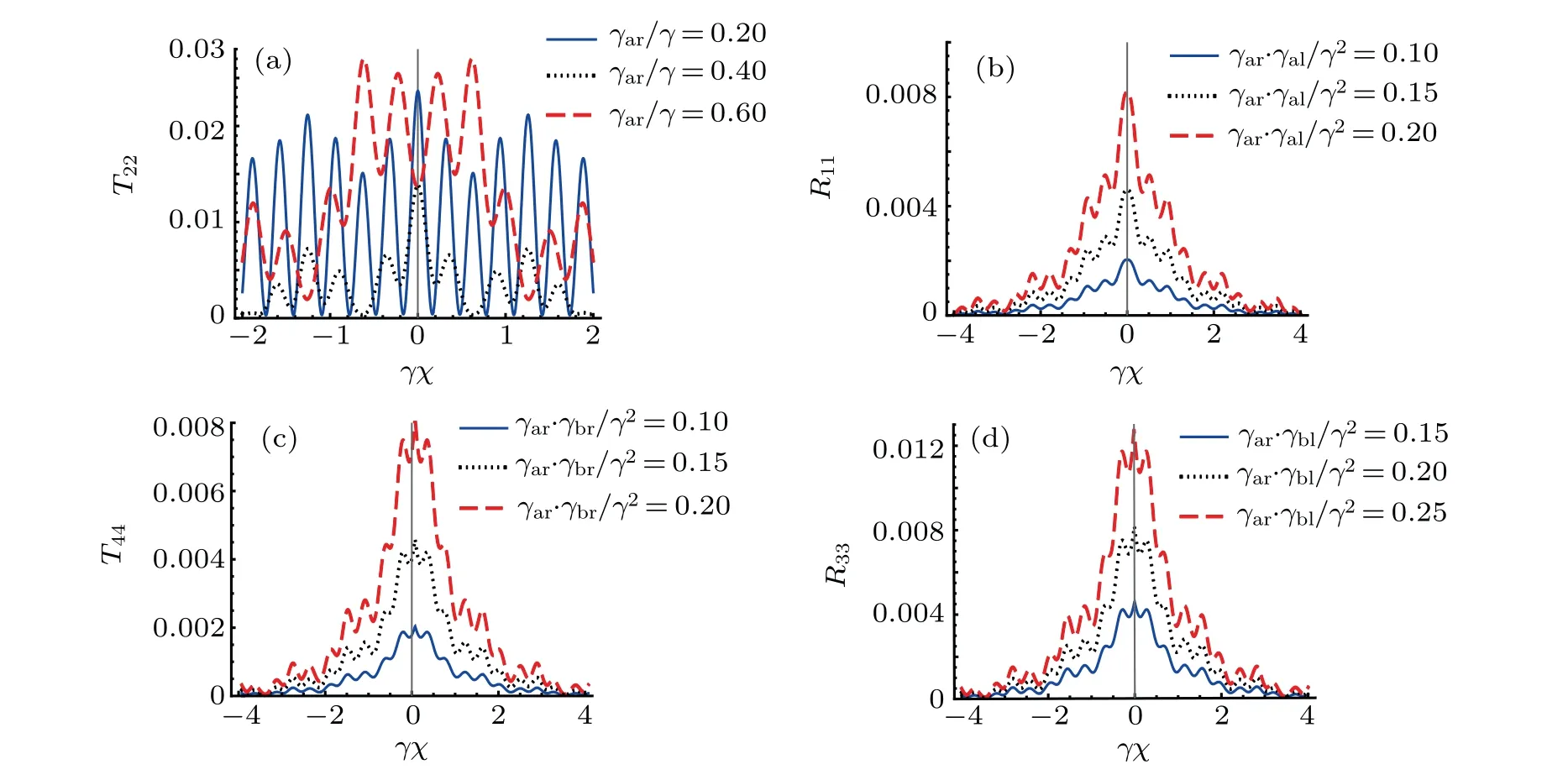
Fig.4. The(a)T22,(b)R11,(c)T44,and(d)R33,as functions of relative coordinate γx. The other parameters are Ω =vp=100γ,vk=110γ,U =10γ.

In order to discuss the transfer rate of photon from waveguideainto waveguideb,we introduce the definition of routing probability as follows:

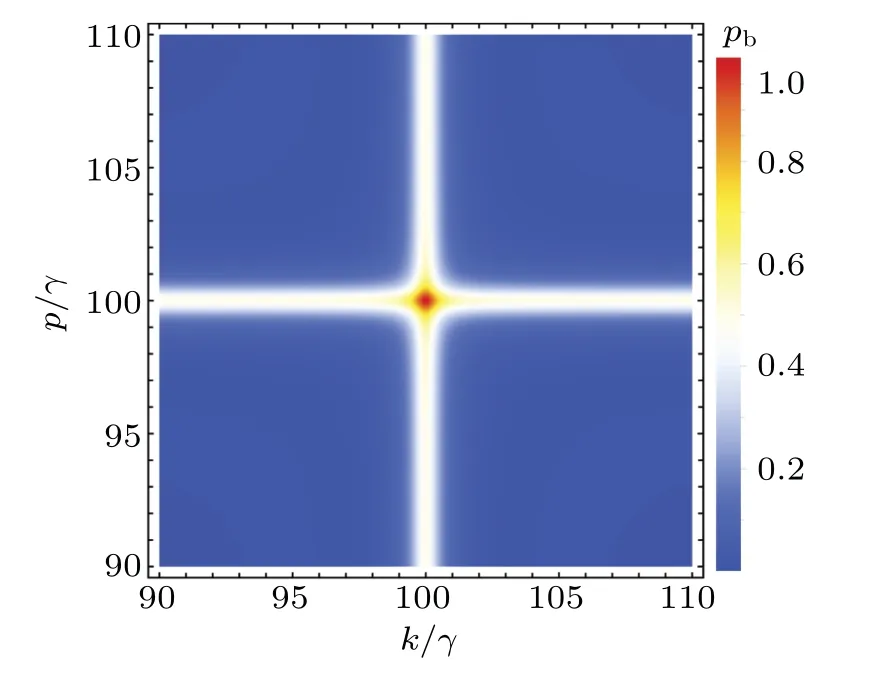
Fig.5.The probability Pb of the input photons from port 1 routed to port 3 as a function of energy vk and vp at the maximally chiral couplings γar=γbr=γ/2.Other parameters are setting as follows:Ω =vp=100γ,vk=110γ,U=10γ.

4. Discussion and conclusion

In summary, we have presented the exact analytic solution of few photons in two one-dimensional waveguides chirally coupled by a nonlinear cavity. Since the Kerr-type nonlinearity has no effect at the single-photon level, the singlephoton routing is not different from that of a two-level atom in two one-dimensional waveguides.[59]Interestingly,at the twophoton level,through some appropriate special inputs,we have measured the transmission, reflection and transfer characteristics of two photons. When two identical resonant photons(vk=vp=Ω) are incident, with the change of the parameterγar/γ, the transmitted photons thus change from bunching to antibunching, and back to bunching. Hence the nonlinear cavity can induce either an effective repulsion or attraction between two transmitted photons. In addition, atx=0, the antibunching inR11for allγarandγalin fact has analogous physical source as the antibunching experimentally.[60]At the same time,T44andR33show an anti-bunching effect different from the previous two-level quantum emitter,[59]that is,it is always in the bunching effect. Surprisingly, when the total frequency of the two incident photons resonates with the twophoton cavity field (vk+vp=2+U),R11,T22,R33, andT44have bunching effects with anyγar,γal,γbrandγbl. This shows that the role of bound states will be greater in two-photon resonance. However, the bound state has no contribution to the routing rate.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 11975095, 12075082, and 11935006) and the Science and Technology Innovation Program of Hunan Province,China(Grant No.2020RC4047)