Passively stabilized single-photon interferometer
2022-11-21HaiLongLiu刘海龙MinJieWang王敏杰JiaXinBao暴佳鑫ChaoLiu刘超YaLi李雅ShuJingLi李淑静andHaiWang王海
Hai-Long Liu(刘海龙) Min-Jie Wang(王敏杰) Jia-Xin Bao(暴佳鑫) Chao Liu(刘超)Ya Li(李雅) Shu-Jing Li(李淑静) and Hai Wang(王海)
1The State Key Laboratory of Quantum Optics and Quantum Optics Devices,Institute of Opto-Electronics,Shanxi University,Taiyuan 030006,China
2Collaborative Innovation Center of Extreme Optics,Shanxi University,Taiyuan 030006,China
A single-photon interferometer is a fundamental element in quantum information science.In most previously reported works,single-photon interferometers use an active feedback locking system to stabilize the relative phase between two arms of the interferometer. Here,we use a pair of beam displacers to construct a passively stable single-photon interferometer.The relative phase stabilization between the two arms is achieved by stabilizing the temperature of the beam displacers.A purely polarized single-photon-level pulse is directed into the interferometer input port. By analyzing and measuring the polarization states of the single-photon pulse at the output port,the achieved polarization fidelity of the interferometer is about 99.1±0.1%. Our passively stabilized single-photon interferometer provides a key element for generating highfidelity entanglement between a photon and atomic memory.
Keywords: passively stable,single-photon interferometer,atom–photon entanglement,polarization fidelity
1. Introduction
In a single-photon interferometer, photons have the possibility of propagating in both channels,[1]by stabilizing the optical path difference between the two channels, stable interference can be achieved. Single-photon interferometers have important applications in the generation of atom–photon entanglement.[2–7]When an atomic ensemble is placed inside a single-photon interferometer the Raman photons,which spontaneously emitted by the atomic ensemble,[8]can propagate along both channels with horizontal polarization and vertical polarization(HandV),respectively.The photons of these two polarizations are coupled at the polarizing beam splitter to form a qubit,[9–13]which can thus be used for atom–photon entanglement.[14–20]
In these studies,[2,3]two polarizing beam splitters are using as the beam combiner of the interferometer. Because the two arms are independent of each other, the optical path difference between the two arms needs to be actively stabilized in this kind of interferometer. The scheme to stabilize the optical path difference is obtained in the feedback signal by detecting the phase difference between two interferometer’s arms,then by using this feedback signal,a stable interferometer can be achieved.[21,22]However,the active locking scheme faces the problems of filtering out the influence of the locking light noise on the experimental signal and the limited stability due to the wide locking light linewidth. The interferometer we used consists of two beam displacers that allow for passive stabilization of the phase. A single-photon interferometer is an essential element for generating entanglement in atomic ensembles, and the stability of the two-arm interference visibility plays a crucial role in the quality of entanglement between a photon and atomic memory.[23,24]In experiments that use a single-photon interferometer to generate atom–photon entanglement, the entanglement fidelity is typically 2.6.[25–29]The entanglement fidelity can be affected by the quality of the interferometer’s polarization fidelity,[30]optical noise,[31]and phase compensation of optical components.Among these influencing factors,the polarization fidelity of a single-photon interferometer is the most important one. Accurate observation of single-photon interferometer polarization fidelity can provide a reference for improving the fidelity of atom–photon entanglement. Currently, two spatial modes of polarized photons associated with atomic magnetically insensitive spin waves are mapped into one spatial mode using a single-photon interferometer in long-lived atom–photon entanglement study. A passively stabilized interferometer consisting of a pair of beam displacers can greatly simplify the experimental system of atom–photon entanglement. The polarization fidelity and the long-term stability of the polarization visibility of the interferometer are necessary conditions for the preparation of high-quality atom–photon entanglement sources, especially in practical long-distance quantum communication networks.[32–35]But the polarization fidelity and temporal stability of passively stabilized single-photon interferometers still have not been reported in detail experimentally.
In this paper,a passively stabilized single-photon interferometer consisting of a pair of beam displacers is constructed.Then the polarization visibility and polarization fidelity of the single-photon level input signal are experimentally measured.The stability of the system is determined by the temperature stability of beam displacers because there is no active locking. In contrast to a single-photon interferometer consisting of a pair of polarizing beam splitters,our design can avoid the use of an active locking system, which meets the experimental requirements for stabilizing atom–photon entanglement in atomic ensembles by passive stabilization only. The polarization fidelity of the interferometer we demonstrated in this work is up to 99.1%±0.1%. Thus, the experimental technical requirements are greatly simplified.The results of this paper will clearly demonstrate that the polarization interferometer we design will not limit the fidelity of atom–photon entanglement and provide a basis for further improvement of entanglement fidelity between a photon and atomic memory in the future.
2. Theoretical analysis
For convenience and practicality, we take a singlephoton-level pulse by attenuating the coherent light pulse as an example. Since the photon number distribution of coherent light obeys the Poisson distribution,the probability that a light pulse with an average photon numberμcontainsnphotons isP(n)=e-μμn/n!. Therefore,the proportion of single photon pulses to optical pulses(nonnull pulses)is

The smaller the average photon number is,the higher the proportion of single photons in the light pulse,but the smaller the average photon number leads to an increase in the number of empty pulses and a decrease in the number of single photon pulses. Through the analysis, when the average photon number is aboutμ=0.01,the probability of a pulse contains one photon is about 0.99%, the probability of a pulse containsnphotons is about 0.995%(n ≥1), the single photon pulse accounted for approximately 99.5% of the proportion of light pulses, which means that the weak single-photon-level pulse is a single photon source.[36,37]

Fig.1. Schematic diagram. SPLP:single-photon-level pulse;HWP1/HWP2:the first/second half-wave plate;BD1/BD2: the first/second beam displacer;PBS: polarizing beam splitter; SPD1/SPD2: the first/second single photon detector;1/2/1′/2′: optical channel.
As in Fig. 1, a|H〉(|V〉) polarized single-photon-level pulse passes through the first half-wave plate(HWP1)with a polarization angle of 22.5°,and the state function of the single photon can be described as

After PBS,|H〉and|V〉polarization single photons are detected by single photon detectors (SPD1 and SPD2) with detection probabilities of cos2[(φ1+φ2)/2] (sin2[(φ1+φ2)/2])and sin2[(φ1+φ2)/2](cos2[(φ1+φ2)/2]),respectively.To ensure the stability of the single photon interferometer, the stability of the phase difference introduced by the beam displacer system needs to be exactly controlled. Changing the crystal length by controlling the temperature of the beam displacers, the optical path difference between the two channels can be adjusted to the integer multiple of the wavelength, whereφ1+φ2=2nπ.
3. Experimental setup
As shown in Fig. 2, the coherent light output from the diode laser (DL Pro, Toptica Photonics) at wavelength of 795 nm is divided into two beams by a PBS.A small amount of the light is injected into the Rb atomic saturated absorption system to lock the laser, and the other portion of the light is used to analyze the single-photon interferometer system. A set of acousto-optic modulators(AOM1 and AOM2)are controlled by a 100 ns square wave pulse, which generated from a field programmable gate array (FPGA), to change the continuous coherent light (with a power of 260 μW) into coherent light pulses. Then the coherent light pulses are attenuated into single-photon-level pulses by three 100 dB neutral optical attenuator (NOA). The single-photon-level pulses are injected into the interferometer system through a single-mode fiber(SMF)after polarization modulation by the first quarterwave plate(QWP1)and the first half-wave plate(HWP1).

Fig. 2. Experimental setup. SAS: saturated absorption system; LD: diode laser; HWP: half-wave plate; PBS: polarizing beam splitter; AOM:acousto-optic modulators; NOA: neutral optical attenuator; QWP: quarter-wave plate; SMF: single mode fiber; PC: phase compensation system;BD1: beam displacer;SPD:single photon detector;PAM system: polarization analyzing and measuring system.
The second half-waveplate (HWP2) and the phase compensation system in the interferometer system are used to compensate for the phase change caused by the optical fiber. The angles of the third half-wave plate(HWP3)and the fourth halfwave plate(HWP4)are polarization matched by a polarization check system that consist of a pair of Glan prisms with an extinction ratio of 1/10000, and the combined extinction ratio reaches 1/1000. The first beam displacer (BD1) and the second beam displacer(BD2)are collimated strictly,insulated by polysulfone material shells,and temperature controlled by high-precision temperature controllers(TED 200C,Thorlabs)to ensure high stability of the polarization visibility and fidelity. A polarization analysis and measuring (PAM) system consisting of a quarter-wave plate QWP2, a half-wave plate HWP5, a polarizing beam splitter, the first single-photon detector(SPD1)and the second single-photon detector(SPD2)is used to perform polarization analysis measurements of singlephoton level light pulses after passing through the interferometer. The overall detection system is placed in a dark room to avoid the influence of environment light. The polarizing beam splitter for projection measurements has an extinction ratio of 1/1000 to ensure the accuracy of the analytical interferometer performance.
4. Experimental results
The diode laser is locked to the87Rb|52S1/2,F=1〉→|52P1/2,F= 1〉resonance frequency. The optical power is adjusted to 260 μW by adjusting the half-wave plate, which is then attenuated by three NOA so that the total count rate of single-photon detectors after the interferometer system is 70 kHz. The quantum efficiency of the single-photon detectors is 68%, and the average photon number of a single pulse(100 ns)is 0.01,approximating a single-photon source.The obtained single photons that polarization modulated by the first quarter-wave plate (QWP1) and the first half-wave plate (HWP1) are injected into the interferometer, the temperature of BD1 is set to 33.00°C while the temperature of BD2 is adjusted. The count of the single photon through the PAM system against the temperature change of BD2 is recorded. Figures 3(a) and 3(b) show the counts for pure single photon state|H〉and|V〉entering through the interferometer system projected to the|H〉and|V〉polarization directions, respectively. The count value and the theoretical calculation (Eqs. (5) and (6)) are in good agreement. From Figs.3(a)and 3(b),we can find that the polarization visibility(V=(CH-CV)/(CH+CV))reaches 98.9±0.3%without any background noise subtraction. The overall count stability is very good,and the average deviation of the count is only 3.9%.Eliminating the effects of dark counting noise(50 Hz)and imperfect dark room light blocking (110 Hz), the polarization visibility can reach more than 99.4±0.3%. Some other influencing factors are the imperfect extinction ratio of the beam displacers, polarizing beam splitter and half-wave plate combination(HWP3 and HWP4).
We further demonstrated the polarization fidelity experiments of the six poles of the Bloch sphere,corresponding six input states|H〉,|V〉,|A〉,|D〉,|L〉, and|R〉. The temperature of BD1 is set to 33.00°C while temperature of BD2 is set to 36.11°C to maximize the|H〉(|V〉) polarization count of the photons after the pure state single photon pulse of|H〉(|V〉)passes through the interferometer system. The density matrixρoutof the single photons is reconstructed by means of quantum state tomography by analyzing the photon counts passing through the interferometer in three mutually unbiased bases|H〉–|V〉,|A〉–|D〉, and|L〉–|R〉, whereH,V,A,D,L,andRdenote horizontal, vertical, antidiagonal (-45°), diagonal (45°), left circular, and right circular polarizations, respectively. The fidelity of the quantum state is defined as the overlap of the density matrixρoutwith the ideal input state|ψi〉:Fst=〈ψi|ρout|ψi〉.[38]The fidelities of the six input states are listed in Table 1, and the measured average fidelity is up to 99.1±0.1%without any noise correction.
We finally investigated the temporal stability of the interferometer by injecting photons in the pure state of|H〉(|V〉)into the interferometer and setting the temperature of BD1 to 33.00°C and BD2 to 36.11°C. The|H〉(|V〉) polarization count of the photons passing through the interferometer system is used to monitor the stability of the polarization visibility. We measured the counts every six minutes and recorded five sets of data each time. The results are shown in Fig.4:the fluctuation of|H〉(|V〉)polarization counts are less than 1%in 8 hours, with highly stable polarization visibility (fluctuation less than 0.5%).
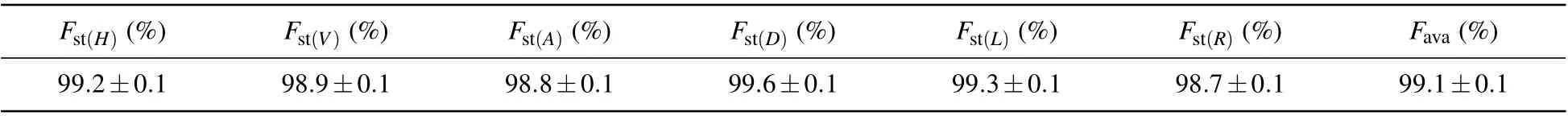
Table 1. Quantum state fidelities of the six input polarization states. Fst(X) are the measured state fidelities for six different input polarized states of photons(X =H,V,A,D,L,R)without any noise correction;Fava=(Fst(H)+Fst(V)+Fst(A)+Fst(D)+Fst(L)+Fst(R))/6 is the average fidelity. The errors are obtained by Monte Carlo simulation which takes into account the statistical uncertainty of photon counts.

Fig.3. Counts of single-photon detectors against the temperature change of BD2. (a)Counts of single-photon detectors projected into the|H〉and|V〉 polarization directions after the |H〉 pure state single-photon passes through the interferometer system; (b) Counts of single-photon detectors projected into the|H〉and|V〉polarization directions after the|V〉pure state single-photon passes through the interferometer system.
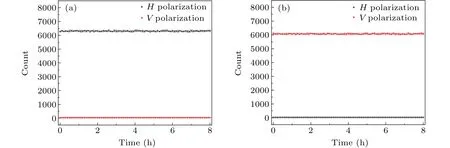
Fig.4. Temporal stability of the interferometer. (a)Counts of single photons in the|H〉pure state after passing through the interferometer system;(b)counts of single photons in the|V〉pure state after passing through the interferometer system.
5. Conclusion
In this paper, we do some performance testing of a passively stable single-photon interferometer consisting of a pair of beam displacers. The polarization visibility can reach 98.9±0.3%when a|H〉(|V〉)pure photon passes through the interferometer. The polarization fidelity of the interferometer is up to 99.1±0.1%while the fluctuation of polarization visibility is less than 0.5% in at least 8 hours. The experiments show that this polarization interferometer has good polarization maintenance characteristics. The results clearly show that the polarization interferometer is not the limiting factor for the fidelity of atom–photon entanglement while the noise of the optical channels and the quality of phase compensation of other optical components are the main limiting factors. This work proved that the beam-displacer interferometer is a simple and reliable method for realizing the long-term atom–photon entanglement experiment.
Acknowledgments
Project supported by the Ministry of Science and Technology of China(Grant No.2016YFA0301402),the National Natural Science Foundation of China (Grant No. 12174235),and Shanxi“1331 Project”Key Subjects Construction.
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- A design of resonant cavity with an improved coupling-adjusting mechanism for the W-band EPR spectrometer
- Photoreflectance system based on vacuum ultraviolet laser at 177.3 nm
- Topological photonic states in gyromagnetic photonic crystals:Physics,properties,and applications
- Structure of continuous matrix product operator for transverse field Ising model: An analytic and numerical study
- Riemann–Hilbert approach and N double-pole solutions for a nonlinear Schr¨odinger-type equation
- Diffusion dynamics in branched spherical structure
