A study of cavitation nucleation in pure water using molecular dynamics simulation

Hua Xie(谢华) Yuequn Xu(徐跃群) and Cheng Zhong(钟成)

1School of Water Resources and Hydropower Engineering,Wuhan University,Wuhan 430072,China

2Hangzhou Water Resources and Hydropower Survey and Design Institute Co.,Ltd,Hangzhou 310016,China

3College of Chemistry and Molecular Sciences,Wuhan University,Wuhan 430072,China

To discover the microscopic mechanism responsible for cavitation nucleation in pure water, nucleation processes in pure water are simulated using the molecular dynamics method. Cavitation nucleation is generated by uniformly stretching the system under isothermal conditions,and the formation and development of cavitation nuclei are simulated and discussed at the molecular level.The processes of energy,pressure,and density are analyzed,and the tensile strength of the pure water and the critical volume of the bubble nuclei are investigated. The results show that critical states exist in the process of cavitation nucleation. In the critical state, the energy, density, and pressure of the system change abruptly, and a stable cavitation nucleus is produced if the energy barrier is broken and the critical volume is exceeded. System pressure and water density are the key factors in the generation of cavitation nuclei. When the critical state is surpassed, the liquid is completely ruptured, and the volume of the cavitation nucleus rapidly increases to larger than 100 nm3; at this point,the surface tension of the bubble dominates the cavitation nucleus, instead of intermolecular forces. The negative critical pressure for bubble nucleation is-198.6 MPa,the corresponding critical volume is 13.84 nm3,and the nucleation rate is 2.42×1032 m-3·s-1 in pure water at 300 K.Temperature has a significant effect on nucleation: as the temperature rises,nucleation thresholds decrease,and cavitation nucleation occurs earlier.

Keywords: cavitation nucleation,pure water,molecular dynamics,tensile strength

1. Introduction

Cavitation refers to the physical phenomenon that takes place when the pressure of a liquid falls below a certain critical value: a cavitation nucleus is generated,which grows into a cavitation bubble.[1]It has been widely accepted that cavitation is due to the existence of weak points in a liquid,and that when the liquid pressure drops to a certain value, these weak points are pulled apart by negative pressure, causing cavitation to be generated.[2,3]In natural water, impurities such as microparticles,dissolved gases,microbubbles,dust,etc. make up the cavitation nuclei that are usually the weak points.[4,5]However, in pure water, the mechanism responsible for generating cavitation bubbles and cavitation nuclei is entirely different from that of natural water.

Water is a strongly cohesive liquid due to the hydrogen bond between its molecules. Many researchers have investigated tensile strength and nucleation in pure water through theoretical and experimental methods.[6]Most researches have concentrated on two issues:one is the way in which cavitation nuclei are generated in pure water,and the other is the tensile strength of pure water. While the answers have varied widely,no definitive explanation or consistent opinion has been obtained so far.

Brennen[6]stated that the tensile strength could reach 103MPa using the method of the potential tensile strength of a pure liquid. Classical nucleation theory(CNT)[7–9]holds that the thermal movement of molecules leads to local low-density voids in the liquid. When the size of the holes in the liquid increases beyond a certain critical value,they rapidly develop into cavitation.The tensile strength of pure water is reported to be 168 MPa at 20°C.[10]Kwaket al.[11,12]proposed a different nucleation model from CNT.According to Kwak’s model,superheating of the liquid causes molecules with high energy to gather together to form molecular clusters. When the clusters grow to a certain size, they reach an unstable state and spontaneously expand into bubbles. Kwak calculated that the tensile strength of pure water is 27.3 MPa at 20°C, which is close to the result of Briggs’s experiment at 277 atm.[13]

A variety of experiments have been carried out to study the cavitation nucleation process, and the tensile strength of pure water obtained by most experiments is in the range of dozens to hundreds of atmospheric pressures.[6,14,15]The difficulty in measuring the tensile strengths of liquids by experiment is that the liquid quality greatly affects the tensile strength test results, and it is very difficult to achieve absolutely pure liquids. However, since the interface between the liquid and the wall of the container is more fragile than the interior of the liquid,the first batch of bubbles is always generated at the interface between the liquid and the container wall,not in the interior of the liquid.

Molecular dynamics (MD) simulation provides a more direct and effective way to study the nucleation of bubbles from the microscopic perspective. It has been extensively used to study the nucleation of Lennard–Jones liquids[16–19]and nanobubbles.[20–22]Classical molecular dynamics is a computer simulation method used to study the equilibrium and transport properties of a classical many-body system by solving Newton’s classical equations of motion for each component.[23]A particle trajectory in the microscopic state can be predicted using MD by numerical integration of the classical equations of motion,[24]and the macroscopic properties,such as the structural,kinetic,and thermodynamic properties of the material can be calculated using the methods of statistical physics.

Most researchers have investigated the nucleation of liquid argon using MD simulation,[18,19,25–30]since the interactions between liquid argon atoms are easy to describe. The results showed that the nucleation rate of liquid argon obtained by MD simulation is 7–9 orders of magnitude higher than that obtained by CNT[26,27]and that nucleation is affected by temperature.[27]

With the ongoing development of different molecular water models,cavitation in water is a hot topic in the simulation of molecular dynamics. Gu[15]studied the inception of cavitation using MD.Gonzalezet al.[31]simulated cavitation nucleation in water and proposed two new methods for obtaining the cavitation volume using the grid method. Wanget al.[32]simulated water cavitation in a controlled volume. Liuet al.[33]investigated the formation and collapse of nanobubbles and the role of nanoparticles in ultrasonic polishing. Liet al.[34]discussed the effects of nanoparticles on the cavitation inception of water. Pellegrinet al.[35]examined the effect of the wetting angle on the nucleation of vapor bubbles in a confined Lennard–Jones fluid under negative pressure in a cubic chamber. Wuet al.[36]studied the nature of shockwave-induced cavitation bubble collapse to determine how the variation of nanoscale bubble size and entrapped gas density affects bubble dynamics. Zhanet al.[24]simulated the compression and collapse processes of microscopic bubbles under impacts at different velocities. Dockaret al.[37]investigated the shockinduced collapse of various surface nanobubble sizes and contact angles.

In this study, the molecular dynamics method is used to simulate the process of cavitation nucleation in pure water.The generation and development of cavitation nuclei are simulated at the molecular scale,and the key parameters,such as energy, pressure, the volume of the cavitation nucleus, density, surface tension, etc. are analyzed. This article attempts to reveal the microscopic mechanism responsible for cavitation nucleation in pure water,clarifying the effects of various parameters on cavitation nucleation and the critical state.

2. Simulation methods

2.1. Steps of molecular dynamics simulation

The simulation of molecular dynamics usually involves four stages: (i) selection of an appropriate water molecule model; (ii) preprocessing of the simulation, selecting the appropriate molecular force field to describe the interaction between molecules, generating the initial configuration of the simulated system, setting the boundary conditions and relevant simulation parameters;(iii)solving the Newtonian equations of motion of all molecules, calculating the force on each molecule, calculating the velocities and positions of the molecules, and obtaining the evolution process of the system over the simulated time; (iv) adoption of the corresponding statistical method to calculate the macroscopic property parameters of the system, such as its total energy, potential energy, kinetic energy, temperature, pressure, etc. The GROMACS software is used for molecular dynamics simulation in this study.

2.2. System simulation and parameters

The interaction between water molecules is composed of two parts: one is the Lennard–Jones(L–J)potential termULJ,and the other is the electrostatic interaction termUε. The TIP4P-FB water model(Subsection 2.3)is selected for the corresponding parameters. The specific expression[23]is

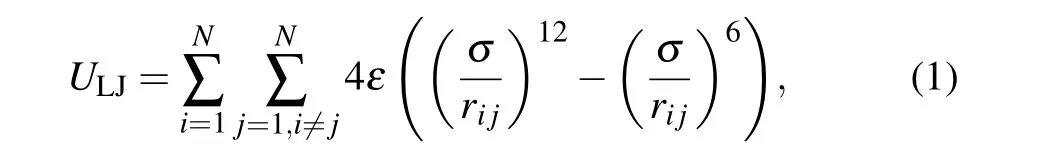
whereri jis the distance between two oxygen atoms,εandσare the representative scales of energy and length,respectively,ε=0.749279 kJ/mol, andσ=0.316555 nm. For hydrogen atoms,these two parameters are set to zero.

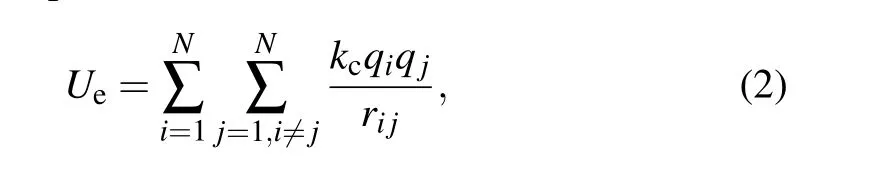
whererijis the distance between two charged particles,kcis the electrostatic constant,kc= 9.0×109N·m2/C2,qis the atomic charge,the charge of hydrogen atomqH=0.5287,the charge of the oxygen atom is set to zero,the charge of type 3 virtual sites is set to-1.05174,and the parametersaandbare set to 0.0898426712735.

The temperatureTin the simulation system is calculated by[38]

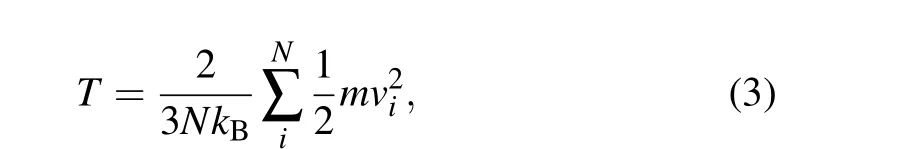
whereNis the total number of molecules,kB=1.380649×10-23J·K-1is the Boltzmann constant,mis the molecular mass,andviis the velocity of each particle.

The system pressurePcan be obtained using the Virial algorithm,[39,40]as follows:

whereρis the number density,drepresents the molecular degrees of freedom,Vis the volume of the simulation system,Uijis the potential function,ri jis the distance between molecules,and the expressionw(r)is called the Virial function.[39]

The system is stretched under isothermal conditions to cause cavitation nuclei to occur in pure water. To reduce the amount of computation, both the L–J potential and the static electric potential energy are truncated; the cutoff distances of the L–J potential and the electrostatic force are 1 nm.The Verlet method[40]is used to determine whether the particles are within the cutoff radius,and the electrostatic long-range force is calculated by the particle mesh Ewald(PME)algorithm.[41]

In general, the larger the size of the simulation system and the larger the number of simulated particles, the smaller the error of the simulation results;however,the amount of calculation increases greatly. For a closed system, a simulation size that is too small leads to large errors in the nucleation rate, and the effects of size can be ignored when the number of molecules in the simulation system is greater than several hundred.[42]Thirty-three thousand and three hundred water molecules are added to a simulation box with a volume of 10 nm×10 nm×10 nm,and periodic boundary conditions are maintained in the three directionsx,y,andz.The initial velocities of the molecules are randomly generated according to a Maxwell distribution atT=300 K,and the rigid geometry of the water molecules is kept unchanged by the linear constraint solver(LINCS)algorithm.[43]

2.3. Molecular models of water

An appropriate water molecular model is the fundamental of molecular dynamics simulations. Although dozens of water models[44–49]have been proposed and developed in recent decades,no one can accurately describe all the important properties of water. Wanget al.[50]optimized the parameters of the original four-point model, TIP4P, using the force balance method and proposed the TIP4P-FB model; and the results are closer to the actual properties of water than those of other models.[50]In this study,the TIP4P-FB model is chosen to simulate the nucleation process of cavitation in pure water by molecular dynamics.

Table 1.Comparison of water model performances at 298.15 K and 1.0 atm.

2.4. The method of production of cavitation nuclei

Two methods are usually used to generate cavitation nuclei: one is to decrease the pressure under isothermal conditions; the other is to increase the temperature at constant pressure. In this work, the pressure is reduced by uniformly stretching the system to promote the generation of cavitation nuclei.

Malyshevet al.[30]and Kuksinet al.[51]pointed out that the liquid tensile strength is weakly correlated with the tensile speed, and the obtained maximum negative pressure is constant when the simulated system of argon atoms is uniformly stretched in three directions at a velocity of(0.001σ～0.004σ)/ps. When the stretching rate increases by an order of magnitude,the maximum attainable pressure only varies by several percent. Based on the research of Malyshevet al.,[30]we have repeated molecular dynamics simulations at tensile rates of 0.1 m/s,0.3 m/s,0.5 m/s,and 0.8 m/s. The influence of the stretching speed on the maximum negative pressure is checked to select a suitable stretching speed.Table 2 shows the mean value of the maximum negative pressure at each stretching speed. It can be seen that from 0.1 m/s to 0.5 m/s, the stretching rate increased 5 times but the corresponding critical pressure only increased by 1.5%, which indicates that the influence of tensile speed on critical pressure is not significant.

The statistical method of significant difference testing was also performed to further evaluate whether the effect of stretching speed on pressure is significant. To test the hypothesis that there is no significant difference in the maximum negative pressure at different stretching velocities,we set the significance levelα=0.05, and the variance test yieldedP=0.71＞0.05,indicating that there is no significant difference. That is to say,in a simulation system with a volume of 10 nm×10 nm×10 nm,when the stretching velocity is 0.1–0.8 m/s,the effect on tensile strength is negligible.

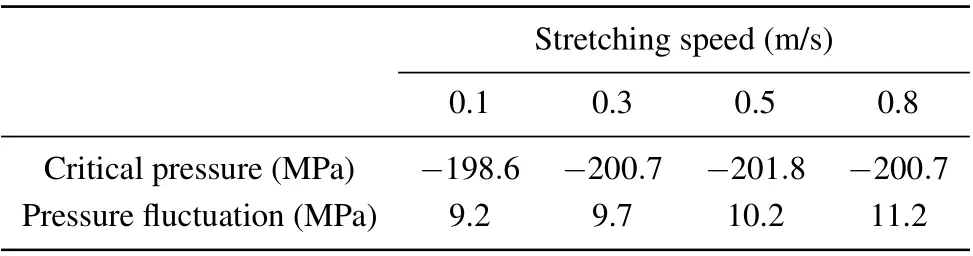
Table 2. Maximum negative pressure of water at different stretching speeds.

Although the influence of stretching speed on tensile strength can be ignored, it can be seen that the smaller the stretching speed,the smaller the pressure fluctuation range. If the speed is below 0.1 m/s,the operating speed of the system is significantly reduced. Therefore, a speed of 0.1 m/s is selected to uniformly stretch the simulation system in the three directionsX,Y,andZ.

2.5. The discrimination and volume of cavitation nuclei

The identification and quantization of voids in the process of bubble nucleation are the key steps in identifying the locations of the cavitation nuclei, tracking the evolution process of each cavitation nucleus,and finding the critical size of the cavitation nuclei. The bubbles can be identified by distinguishing the vapor phase space from the liquid phase space.The Voronoi tessellation method is used in this study,as it has been proved that it can effectively distinguish the vapor–liquid interface with continuous application and improvement.[52–54]

The basic idea of the Voronoi tessellation method is to make vertical bisectors between two adjacent particles of the three-dimensional system by the division method of Tyson polygons. These perpendicular bisectors divide the space into polyhedrons,and each particle is surrounded by a polyhedron;a schematic diagram is shown in Fig.1.

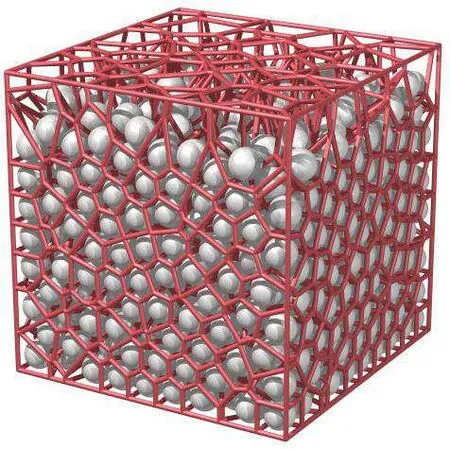
Fig.1. Schematic diagram of the Voronoi tessellation method.[55]

The volume–sphericity relation of the Voronoi polyhedron proposed by Abascal[55]is used to distinguish the vapor and liquid phases of the system and calculate the volume of the bubbles. We can discriminate the cavitation nucleus and calculate the volume of the cavitation nucleus by comparing the volume and sphericity of the Voronoi polyhedron before and after the generation of the cavitation nucleus.

To better describe the method used to identify the cavitation nuclei,figure 2 shows the volume distribution of Voronoi polyhedra before and after the generation of cavitation nuclei in pure water. From Fig.2, at the beginning(t=0 ps), there are no cavitation nuclei in the system; after the generation of cavitation nuclei(t=4200 ps), the peak value of the volume distribution of the polyhedra decreases, the number of small polyhedra decreases, and the number of large polyhedra increases. This takes place because the generation of cavitation nuclei increases the distance between the interface molecules,and the volume of polyhedrons obtained by dividing the interface molecules increases.

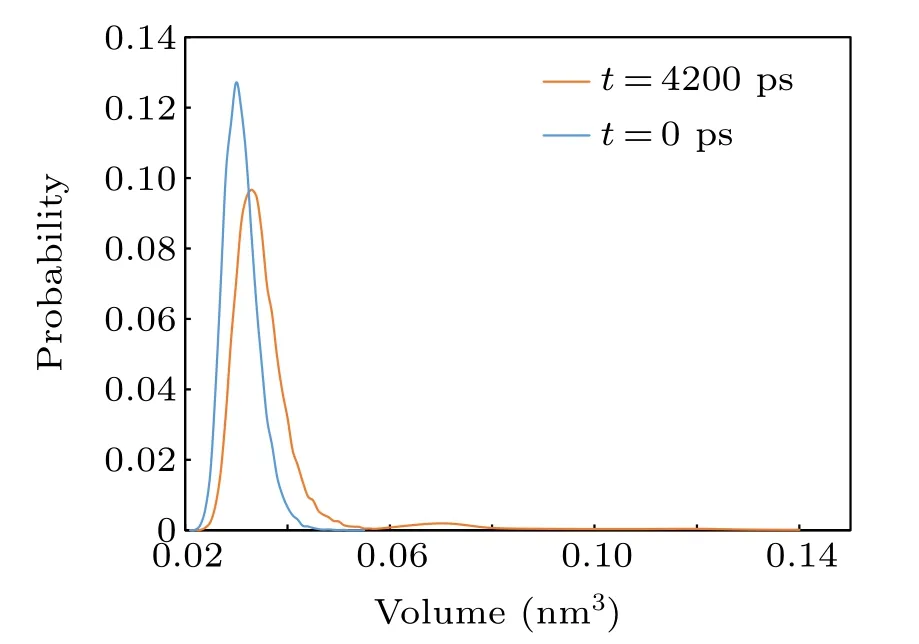
Fig.2. Volume distribution of Voronoi polyhedra before and after cavitation nuclei appear.

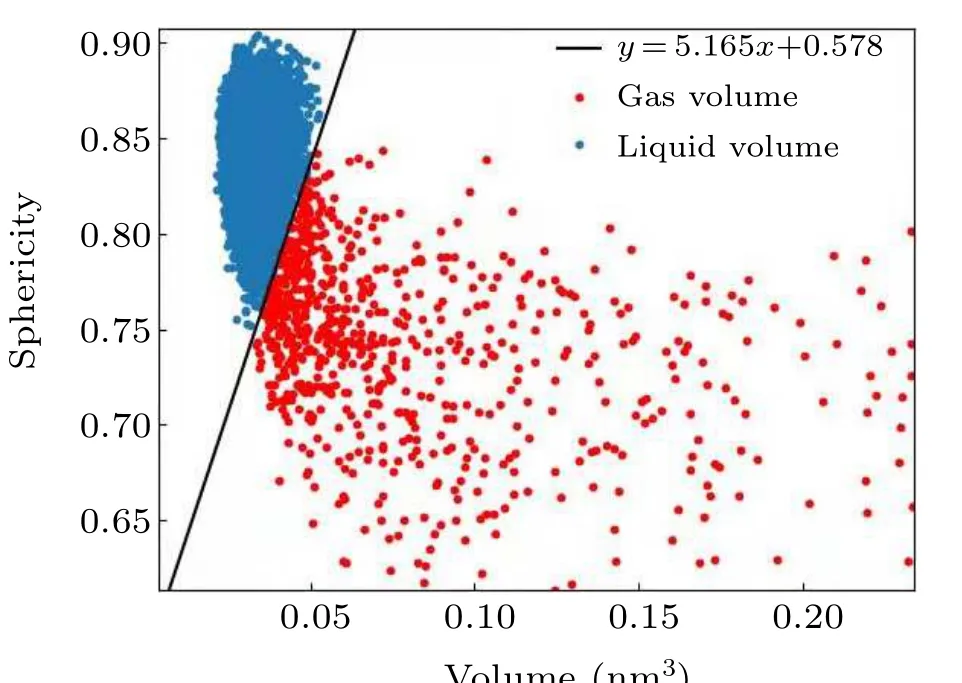
Fig.3. Partition of the gas and liquid Voronoi polyhedra according to the volume–sphericity relationship.

Figure 3 shows the relationship of the gas and liquid fractions to the volume and the sphericity of the polyhedrons. In the case of pure water without nuclei,the distribution of points is relatively concentrated in the upper-left corner of the graph(the blue dots in Fig.3). After cavitation nuclei appear,some points (the red dots in Fig. 3) deviate in the direction of increasing volume and decreasing sphericity; these points constitute the molecules at the interface. Based on the distribution of the Voronoi polyhedra,a straight line can be drawn to distinguish between liquid and gas Voronoi polyhedra. Then,based on the statistical volume of the gas Voronoi polyhedra,the vapor volume can be calculated.

2.6. Preprocessing and simulation

In the initial configuration, since water molecules are randomly added to the simulation system, unreasonably high energy configurations, such as overlaps and large repulsive forces, may exist in the system (see Fig. 4). Before the formal simulation can begin, a relaxation simulation must be carried out so that the system reaches its full equilibrium.An NPT (constant-pressure, constant-temperature) ensemble is used for the relaxation simulation. The temperature is kept at 300 K by a velocity rescaling thermostat,[38]and the pressure is kept at 1 atm by a Berendsen barostat.[56]The relaxation time is 100 ps. The results of the relaxation simulation are shown in Fig. 5. The results for the total energy, density,volume,and pressure indicate that the system reaches equilibrium within 10 ps.

After the system has reached equilibrium, a formal MD simulation of three-dimensional stretching at a velocity of 0.1 m/s is conducted in the canonical ensemble(NVT)so that nucleation is generated under negative pressure in the simulation system. In the whole simulation process, the Newtonian motion equations are solved by the leapfrog algorithm[57]and the temperature is kept stable at 300 K.The simulation lasts for 5000 ps,and the results are recorded and output every 2 ps.

Fig. 4. Initial configuration of the for molecular dynamics simulation(10 nm×10 nm×10 nm).

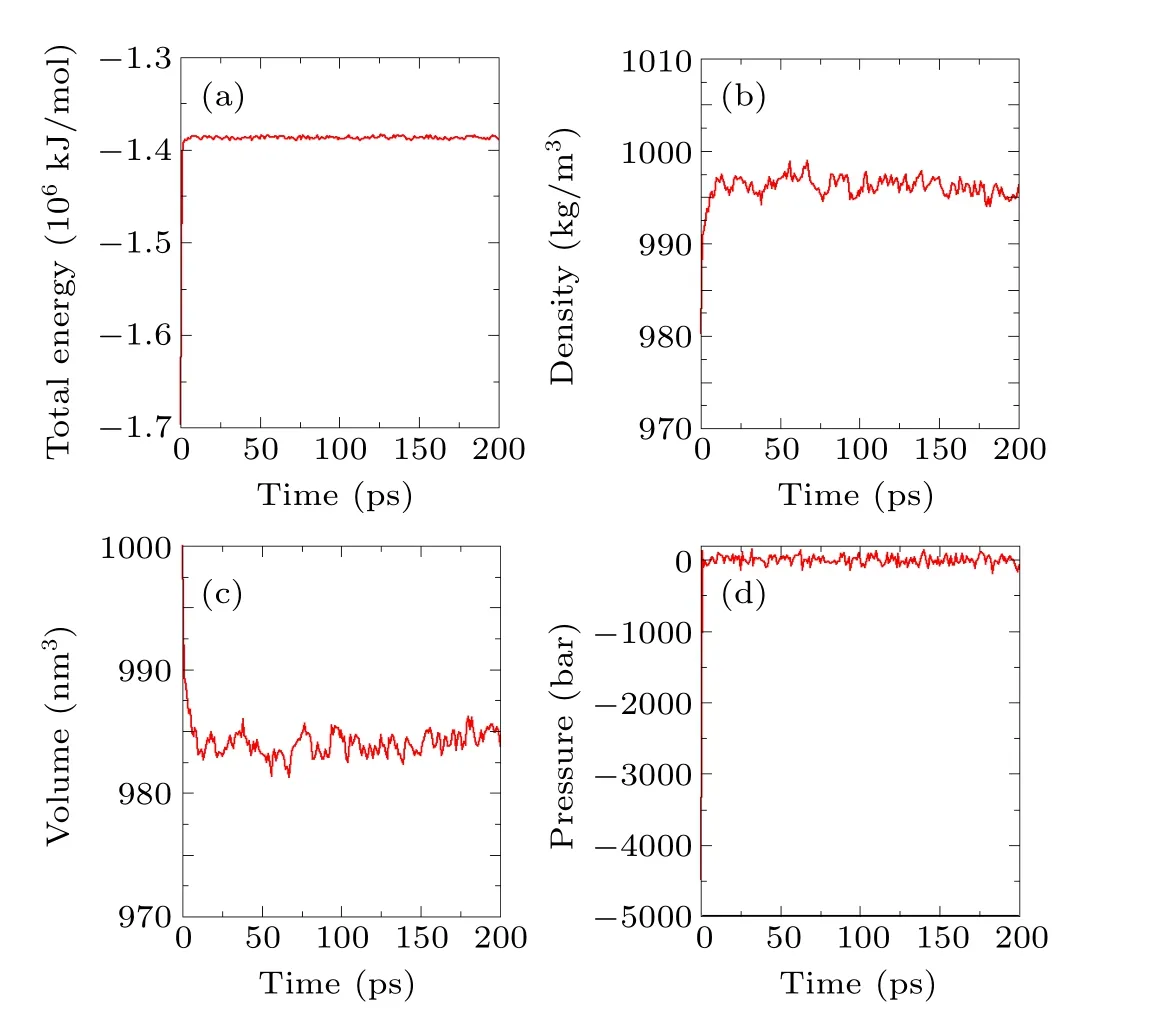
Fig.5. Diagrams of the results of the relaxation simulation.

3. Results and discussion

3.1. The process of bubble nucleation

The generation,growth,and development process of cavitation nuclei in the simulation system can be observed during the molecular dynamics simulation. To facilitate the observation of the internal structure of pure water in the simulation process, a 2 nm thin layer in the simulation center is taken as a molecular configuration section. Figure 6 shows a crosssectional diagram of bubble growth and development in pure water, which can be divided into three stages: (i) at the beginning of the simulation,the system is in equilibrium and the water molecules are evenly distributed in the simulation box after the relaxation of the system(see Fig.6(a)).As the system slowly stretches,some intermolecular voids appear and disappear randomly(as shown in Fig.6(b)). The sizes of the voids generally range from several to dozens of molecules,but they disappear rapidly with the thermal motion of the molecules,and the system is in a metastable state. (ii) As the stretching continues,a relatively obvious void appears inside the system(Fig. 6(c)); the size of the void increases rapidly over a short time(Fig.6(d)),and the system is still in an unstable state.(iii)When the void increases beyond a large size(Fig.6(e)), then the bubble grows slowly, although the system is still stretching,and the system enters a steady state(Fig.6(f)).

In addition,a critical size is found during the growth process.Only when the random void grows larger than the critical size does it continue to develop and rapidly grow into a stable bubble, otherwise, it disappears in the random motion of the molecules. Moreover,the shape of the bubble is relatively irregular during the initial stage; it tends to be more and more spherical in the later periods. This occurs because a sphere is more stable, as it has the smallest surface area and smallest surface energy for voids with the same volume.

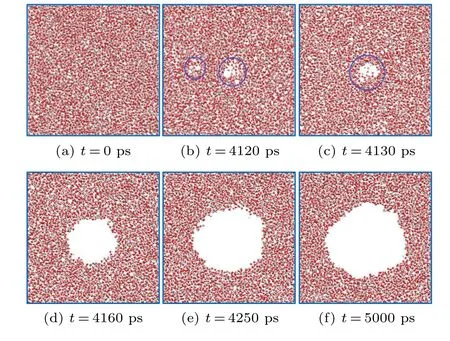
Fig. 6. Cross-sectional diagram of the growth process of a bubble in pure water(10 nm×10 nm×10 nm).

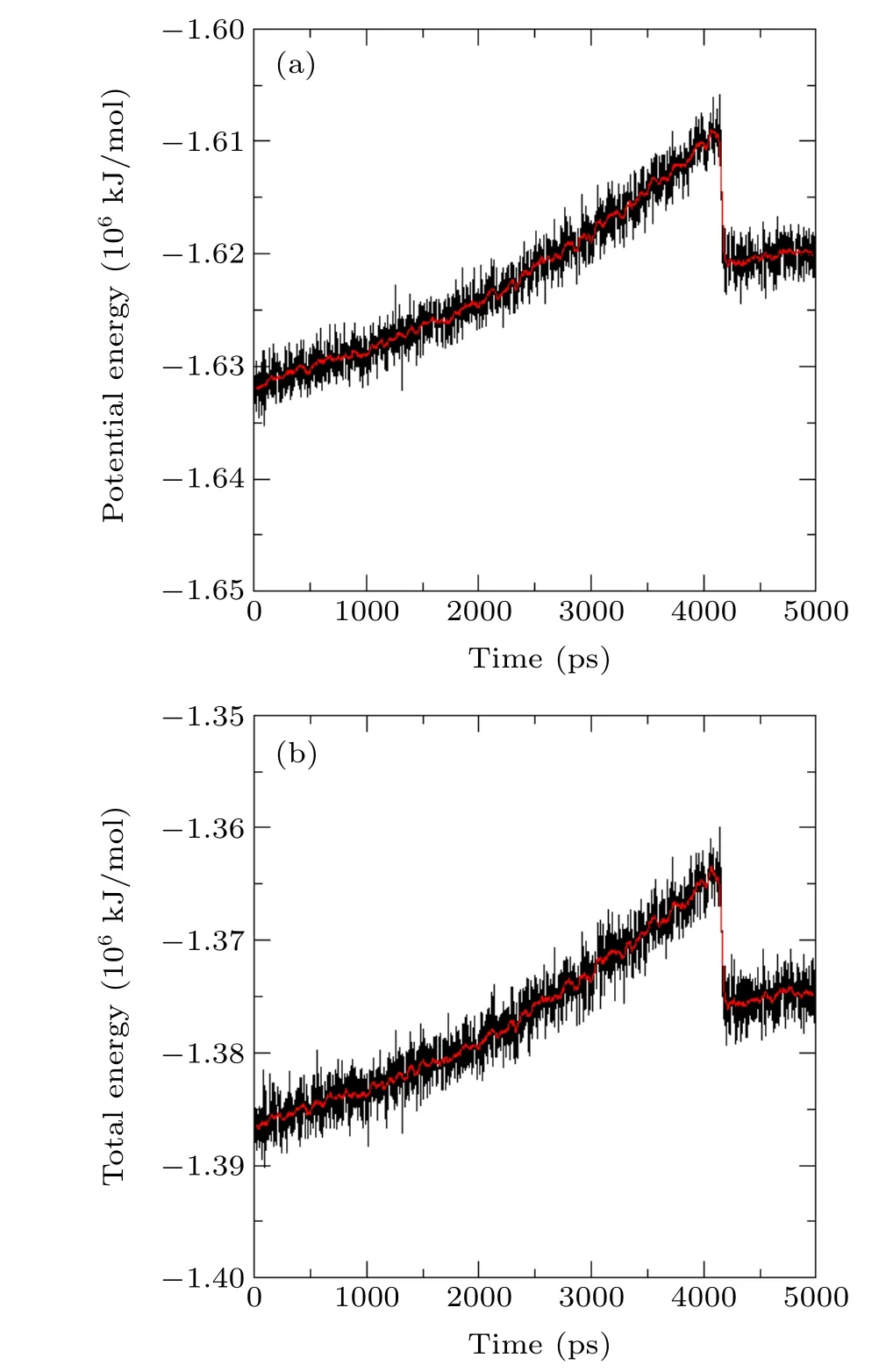
Fig.7. Diagram of system energy change versus simulation time.

3.2. Energy change in the process of nucleation

The energy process corresponding to the process of nucleation is recorded. The total energy of the system is composed of kinetic energy and potential energy. Since the simulation is conducted under the NVT ensemble in which the system temperature is constant, the kinetic energy always fluctuates around a certain constant value. The change in the total energy is mainly due to the potential energy.

The change processes of the potential energy and the total energy are shown in Fig. 7. As the system is stretched,the energy gradually increases;the maximum value appears at about 4160 ps,right at the moment when a stable void is produced; it then decreases instantaneously and finally stabilizes again at 4210 ps. The process of energy change in the system shows a good correlation with the growth and development of the bubble.

The molecular potential energy describes the stability of the constituent material. A lower molecular potential energy means more a stable material and vice versa. However,an increase in the molecular potential energy does not mean that a bubble can be produced. Figure 7 shows that the liquid needs to pass through an energy barrier to complete the process of gas–liquid transition from a metastable liquid to a stable bubble.

3.3. Pressure in the process of nucleation

The change of pressure with time is shown in Fig.8. The pressure of the system changes in three stages: (i) first, as a result of stretching,the pressure slowly drops from the initial atmospheric pressure; intermolecular voids appear and disappear randomly in this period and the system is in a metastable state. This period corresponds to Figs. 6(a) and 6(b). (ii)When the pressure drops to a certain critical point at 4160 ps,a moment that perfectly corresponds to the maximum potential energy and total energy, it reaches a minimum value at-198.6 MPa,then rapidly rises to-60.5 MPa at 4210 ps. The void grows larger than the critical size and the system tends to stabilize, corresponding to Fig.6(d). (iii)Since the system is still stretching, the pressure slowly rises from-60.5 MPa to-55.5 MPa during the period fromt=4250 ps tot=5000 ps,and a stable large bubble nucleus is generated in pure water,corresponding to Figs.6(e)and 6(f).

It can be observed that when cavitation nuclei are produced in pure water, the pressure has to be reduced to a certain critical value. The critical pressure corresponding to the lowest point of the curve is-198.6 MPa, the absolute value of which is the tensile strength of pure water, and the tensile strength simulated by MD is much higher than the experimental value.[6]

To study the effects of different temperatures on the critical pressure of bubble nucleation,six temperature conditions,namely 280 K, 300 K, 320 K, 340 K, 350 K, and 360 K are selected for MD simulation. The simulation results are shown in Figs.9 and 10.

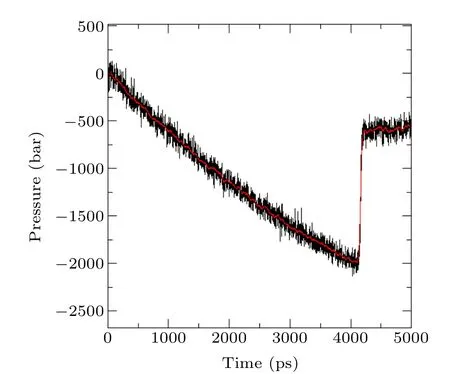
Fig.8. Diagram of system pressure changes versus simulated time.

Fig. 9. Variation of system pressure versus simulated time at different temperatures.

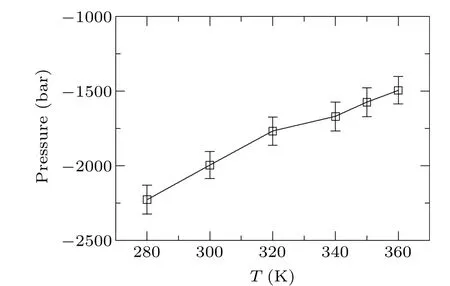
Fig. 10. Critical pressure diagram for the nucleation of pure water at different temperatures.

From Figs. 9 and 10, we find that the higher the temperature, the shorter the nucleation time and the greater the critical pressure. For example, at 280 K,a pressure jump occurs at about 4460 ps and the corresponding critical pressure is-222.6 MPa, while at 360 K,it occurs at 3695 ps, and the critical pressure increases to-149.4 MPa.

Obviously,as the temperature increases,the critical pressure required for nucleation increases,the tensile strength decreases,and cavitation nucleation occurs earlier. The thermal motion of water molecules intensifies with increasing temperature, which increases the probability of the system crossing the energy barrier; as a result, the tensile strength of water is reduced and cavitation is more likely to occur.

In Figs. 8 and 9, a significant pressure ‘jump’ occurs in the process of nucleation. To further analyze the reason for the pressure‘jump’,the volume and density during nucleation are analyzed together in the following sections.

3.4. Bubble volume and nucleation rate

The volume of the void in the process of bubble nucleation is output every 50 ps, as shown in Fig. 11. As can be seen from Fig. 11, the volume of the bubble nucleus increases as stretching continues, while in the early stage (beforet=4000 ps),the bubble grows very slowly and its volume fluctuates by less than 10.0 nm3. When it breaks through the critical volume near 13.84 nm3(t=4140 ps),it grows sharply to 100 nm3(t=4200 ps), meaning that a stable cavity has formed.

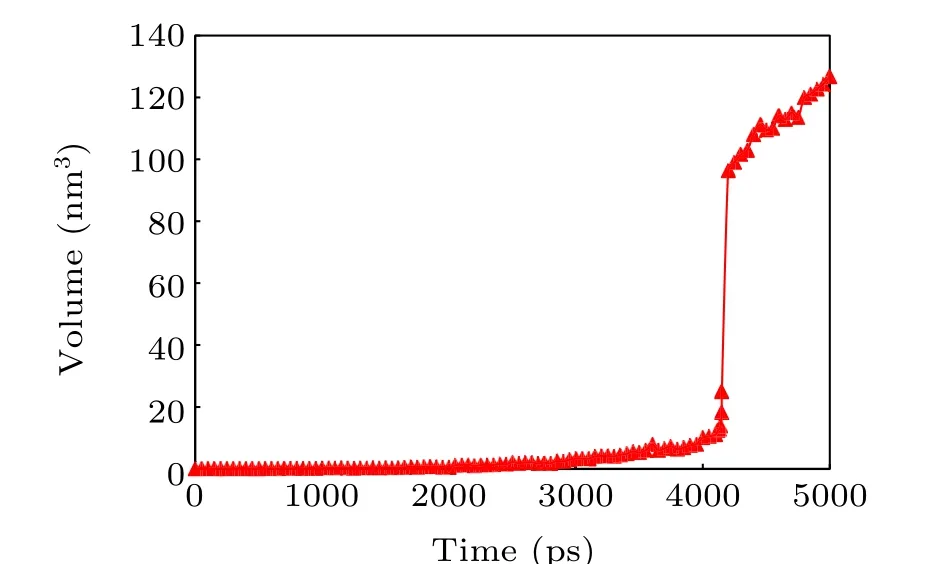
Fig.11. Volume change of the bubble nucleus.

The nucleation rate reflects the difficulty of cavitation in pure water. It refers to the number of cavitation nuclei generated in a unit volume per unit time. The basic equation for the nucleation rate can be derived from the Fokker–Planck equation,[58]and the specific expression[54]is

whereVis the volume of the simulated domain,andτJis the time taken by the bubble to reach the preset threshold size for the first time.

The mean value ofτJobtained from the MD simulation is 4140 ps,the preset threshold size is 100 nm3,and the nucleation rate is 2.42×1032m-3·s-1at 300 K.

3.5. Discussion of the density and pressure jump

When the system is uniformly stretched, it inevitably causes a change of system density and water density;the density can be calculated from the expressionρ=M/V. For the system density,Mis the mass of all the water molecules in the system andVis the volume of the system. For the water density,Mis the mass of the water molecules,excluding the water molecules inside and at the interface of the cavity andVis the volume of the system,excluding the volume of the cavitation voids (shown in Fig. 11). The results for system density and water density are shown in Fig.12.

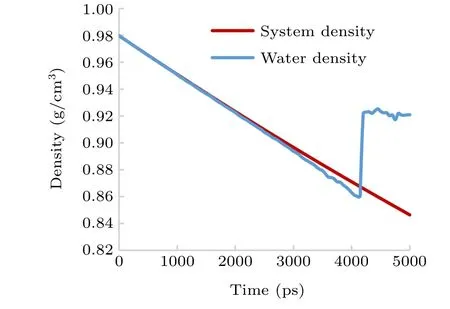
Fig.12. Density change in the process of nucleation.

According to CNT,[8]the decrease of liquid density is more likely to generate voids in the low-density region. As the system is stretched, the system density decreases linearly(Fig.12),and the water density decreases linearly(in the same way as the system density decreases in the initial stage before the steady cavitation nuclei occur),and the decrease of density is favorable to the formation of cavitation nuclei.

As the stretching continues,tiny nuclei begin to randomly appear (see Fig. 6(b)) and more water molecules become the interface molecules of the nucleus; therefore, the water density is a little lower than the system density during this period(see Fig. 12). At this stage, the system pressure continues to decrease under stretching(see Fig.8).

When the water density is decreased to the minimum value of 0.859 g/cm3(nearlyt=4130 ps to 4160 ps),the pressure reaches the critical value-198.63 Mpa (t=4160 ps);at this point, the stretching force exceeds the molecular force of water, and the liquid is completely ruptured. At this moment, the volume of the cavitation nucleus enlarges sharply(see Fig.11)and a stable cavitation nucleus is generated. The water molecules are squeezed by the sudden expansion of the cavitation nucleus volume, causing the water density to rise rapidly and then reach a stable level(mean value 0.922 g/cm3)(see Fig.12),and the corresponding pressure jumps to a stable value of nearly-60.5 MPa (see Fig. 8); the system enters a relatively stable state.

After stable bubble nuclei have been produced, the volume of the cavity exceeds 100 nm3and continues to grow under stretching; during this period, the surface tension of the bubble(instead of other intermolecular forces)dominates the growth of the cavitation nucleus.

The surface tension pressurePscan be calculated by the Laplace equation[8]Ps=2σ/R,whereσ=0.0716 N/m is the surface tension coefficient of water at 300 K,andRis the radius of the cavitation nucleus. After bubble formation occurs,fromt=4200 ps tot=5000 ps,the surface tension changes smoothly from 50.36 MPa to 45.96 MPa with the enlargement of the bubble. The surface tension pressure calculated by the Laplace equation is a good match for the system pressure calculated by the Virial algorithm, which is also a proof of the reliability of the simulation.

The above analysis results show that the decrease of system pressure and water density caused by system stretching are the key factors that promote the generation of cavitation nuclei. After the liquid is completely pulled apart, the volumes of the cavitation nuclei rapidly increase to more than 100 nm3— surface tension then replaces the intermolecular force and plays a dominant role in the growth of the cavitation nuclei; the negative pressure then increases instantaneously,which appears as a“jump”in the pressure curve(see Fig.8).

4. Conclusion

This research uses molecular dynamics techniques to simulate the nucleation process in pure water. Cavitation nucleation occurs through uniform stretching of the system under isothermal conditions. The process of bubble nucleation and the corresponding pressure,energy,and density are analyzed,and the critical nucleation parameters are studied, including the tensile strength of pure water, the critical volume of the bubble,and the nucleation rate. The main conclusions drawn include the following:

(i)There is a critical stage in the process of bubble nucleation. In the critical state,the energy,density,and pressure of the system change abruptly;when the energy barrier is broken and the critical state is exceeded, steady cavitation nuclei are generated.

(ii)The changes of energy and pressure are a good match for the growth and development of the bubble. The negative critical pressure of bubble nucleation in pure water is-198.6 MPa at 300 K.As the void increases beyond the critical volume,13.84 nm3,it rapidly develops into a stable bubble,and the nucleation rate in pure water is 2.42×1032m-3·s-1at 300 K.

(iii)Temperature significantly affects the tensile strength of pure water. As the temperature rises, the critical pressure required for the nucleation of pure water increases, and cavitation nucleation occurs earlier.

(iv) The system pressure and water density are key factors in the generation of cavitation nuclei. Before stable cavitation nuclei form,the pressure depends on the intermolecular force. After the liquid is completely ruptured,the volumes of the cavitation nuclei rapidly increase to more than 100 nm3,and at that point, the surface tension of the bubble dominates the cavitation nucleus instead of intermolecular forces.

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant Nos.51779187 and 51873160).