Robust and intrinsic type-III nodal points in a diamond-like lattice

Qing-Ya Cheng(程青亚) Yue-E Xie(谢月娥) Xiao-Hong Yan(颜晓红) and Yuan-Ping Chen(陈元平)

1School of Physics and Electronic Engineering,Jiangsu University,Zhenjiang 212013,China

2School of Physics and Optoelectronics,Xiangtan University,Xiangtan 411105,China

An ideal type-III nodal point is generated by crossing a completely flat band and a dispersive band along a certain momentum direction. To date,the type-III nodal points found in two-dimensional(2D)materials have been mostly accidental and random rather than ideal cases, and no one mentions what kind of lattice can produce ideal nodal points. Here, we propose that ideal type-III nodal points can be obtained in a diamond-like lattice. The flat bands in the lattice originate from destructive interference of wavefunctions,and thus are intrinsic and robust. Moreover,the specific lattice can be realized in some 2D carbon networks,such as T-graphene and its derivatives. All the carbon structures possess type-III Dirac points.In two of the structures,consisting of triangular carbon rings,the type-III Dirac points are located just on the Fermi level and the Fermi surface is very clean. Our research not only opens a door to finding the ideal type-III Dirac points,but also provides 2D materials for exploring their physical properties experimentally.

Keywords: diamond-like lattice,carbon materials,type-III Dirac points

1. Introduction

Graphene presents a standard model of type-I twodimensional (2D) Dirac point,[1–4]which is crossed by two linear energy bands with inverse slope signs. When the slope sign of one linear band changes from negative/positive to positive/negative along a certain momentum direction, the Dirac point transits from type-I to type-II.[5–7]Type-III Dirac or Weyl points[8–12]are critical topological phases between type-I and type-II points.It is crossed by a flat band,i.e.,its slope is zero,and a normal dispersive band. Thus,the Fermi surfaces of type-III nodal semimetals are all straight lines, exhibiting a diverging density of states.[13]The quasi-particles in this kind of material present highly anisotropic mass with localized states along one direction in the flat band coexisting with massless states moving ballistically.[14–16]While most of their electric and magnetic properties are yet to be unveiled, they have been predicted to greatly enhance the super-conducting gap in Weyl semimetals,[17,18]and they provide a new platform for the study of correlated phases with a flat band.[19–23]Moreover,the type-III nodal points would open a door to the study of analogue black holes in a solid-state environment.[16,24]

Up to now,type-III nodal points have been found in some 2D materials.[25–29]such as SW40,[26]hr-sB,[27]andpenta-NiSb2.[29]However,the nodal points found in them are mostly accidental and random. An ideal type-III nodal points should be crossed by a completely flat band and a dispersive band along a certain momentum direction,and the flat band should be robust,i.e., its flatness is not affected by external perturbations, such as strain. In this sense, all the previous type-III nodal points found in the materials are not ideal cases.

The key point of type-III nodal points is the flat band.As is well known, some special lattices, such as Kagome,[30]Lieb,[31]and coloring-triangle lattices,[32]can generate flat bands. However,these flat bands are actually flat planes filling fully the whole Brillouin zone(BZ)of the 2D materials.[33–37]The flat bands in the type-III nodal points are just flat lines along a certain momentum direction. Although one can obtain type-III nodal points by destroying symmetries of the fullplane flat-band systems,these systems are not good options for generating intrinsic type-III nodal points. Considering that the interesting physical properties and important applications of the critical nodal points,it is very anxious to find intrinsic and robust type-III nodal points in a lattice and relevant materials.

In this paper, we propose a kind of new lattice hosting intrinsic and robust type-III nodal points. The lattice is comprised of one-dimensional (1D) diamond chains, and thus is named diamond-like lattice. By using a tight-binding model,type-III nodal points are produced in 1D diamond chain and 2D diamond-like lattice. The flat bands in the nodal points are induced by the destructive interference of wavefunctions,and thus the nodal points are intrinsic and robust because they are protected by the lattice’s geometry. Then,we demonstrate that the diamond-like lattice can be realized in 2D single-layer carbon networks, such as T-graphene and its derivatives (named T-graphene-1,2,3 here). All the carbon structures indeed possess intrinsic and robust type-III Dirac points. Finally,considering that T-graphene-1 have been synthesized successfully,we propose a routine to fabricate other 2D carbon networks with diamond-like lattice.

2. Type-III nodal points in 1D and 2D diamondlike lattices

The flat bands in type-III nodal points only exist along a certain momentum direction, which means that the flat band has 1D feature. So, we can first consider a 1D lattice with a flat band. Previous studies have indicated that the band structure of a 1D diamond chain,as shown in Fig.1(a),has crossing point of a flat band and a dispersive band.[38,39]One can use a tight-binding(TB)model to describe the electron properties of the 1D chain. If each lattice has only one type of electron orbital,saypz,the Hamiltonian can be expressed as

wherecrepresents the length of primitive cell of the diamondlike lattice. Obviously,a flat band corresponding to the eigenvalueE1is generated. The band structure witht1=1.6 eV andt2=1.2 eV is given in Fig. 1(b). A type-III nodal point appears. The flat band usually originates from the destructive interference of wavefunctions. The inset in Fig. 1(b) shows the charge densities of the quantum states in the flat band.One can find that the electrons are localized on the two sides of the chain, but the middle lattices are empty. This is because the two waves propagating along the chain interfere destructively at the middle lattices[see the positive sign and minus sign of the wavefunction in the inset of Fig.1(b)].[40]

If one extends periodically the 1D diamond chain along the horizontal direction, a 2D lattice can be obtained [see Fig.1(c)]. Because it is comprised of 1D diamond chains,we name the 2D lattice a diamond-like lattice. One can also use Eq. (1) to describe its electronic properties when more hopping energy in the 2D lattice is added,for example,a hoppingt3between the 1D diamond chains. In the 2D case,the expressions of the eigenvalues for Eq.(1)are complicated. However,one can get its specific eigenvalues under some conditions.For example,ifkx=0,the three eigenvalues can be expressed as

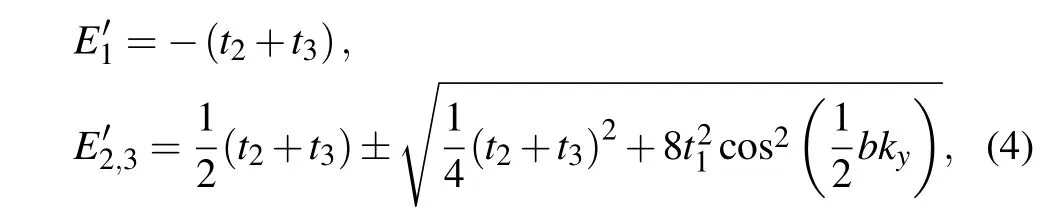
whereaandbrepresent the lattice parameters of the lattice. Ifkx=π/a,the three eigenvalues can be expressed as

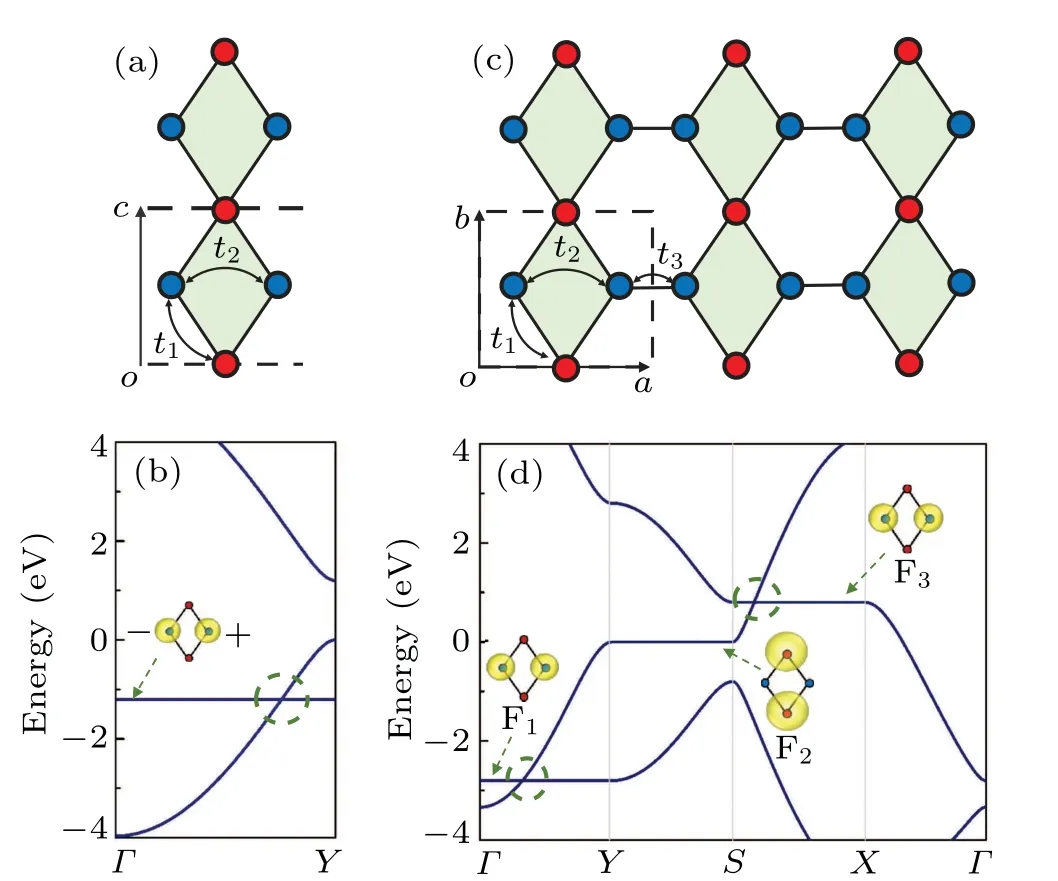
Fig. 1. (a) A 1D diamond lattice, with dashed line representing primitive cells. (b) Band structure of 1D diamond lattice based on Eq. (1) with t1 =1.6 eV and t2 =1.2 eV, with inset showing charge density of quantum state on the flat band(“+”and“-”represent signs of wavefunctions).(c) The 2D diamond-like lattice, with dashed line representing primitive cells. (d) Band structure of 2D diamond-like lattice based on Eq. (1) with t1=1.6 eV,t2=1.2 eV,and t3=1.8 eV,with inset exhibiting charge densities of three quantum states F1,F2,and F3 on the three flat bands.

The band structure of the 2D diamond-like lattice changes with the parameters.Because the flat bands always exist on the three high-symmetry paths mentioned above,one can usually observe type-III nodal points on the three paths. Beside the type-III nodal points, some other topological phases can also be found in the diamond-like lattice.For example,whent2=t3(ort2=-t3), one can obtainE′′1=E′′′1according to Eqs. (4)and (5) (orE′1=E′′′1according to Eqs. (3) and (5)). Then, a triple degeneracy point, crossed by a cone and a flat plane, is formed in the first BZ[the detail can be found in Fig.S1 in the supplementary information(SI)].The triple degeneracy point is located at the high-symmetry pointSorY.

3. Diamond-like lattice in 2D carbon networks and type-III Dirac points in them

The diamond-like lattice in Fig. 1(c) can be realized in 2D carbon networks by utilizing the strong ability to form the bonds between carbon atoms. The simplest carbon structure like diamond-like lattice is T-graphene as shown in Fig.2(a).When a carbon dimmer in the green ellipse in Fig.2(a)along the perpendicular direction shrinks to one site, T-graphene changes into a standard diamond-like lattice. This simple carbon network can evolve into some other structures with diamond-like lattice. For example, when one of the carbon atoms in the horizontal dimmer extends to two atoms along the perpendicular direction, T-graphene evolves into a structure as indicated in Fig.2(b)and is named T-graphene-1 hereafter;when each atom in the green ellipse in T-graphene is replaced by a triangular ring,T-graphene changes into the structure in Fig.2(c)and is termed T-graphene-2; when the atoms in the perpendicular dimers in T-graphene-1 are replaced by two triangular rings,a carbon network called T-graphene-3 is obtained as shown in Fig.2(d).

To deal with the electronic properties of the carbon networks, we perform first-principles calculations within the density functional theory (DFT) formalism as implemented in VASP.[41]The electron–electron interactions were treated within a generalized gradient approximation (GGA) in the form of Perdew–Burke–Ernzerhof (PBE) for the exchange–correlation functional.[42]Electronic wave functions are expanded by using a plane-wave basis set with cut-off energy of 600 eV. The atomic positions are fully optimized by the conjugate gradient method,[43]and the energy and force convergence criteria are set to be 10-6eV and 10-3eV/˚A, respectively. Periodic boundary conditions are used with a 20 ˚A vacuum layer in the direction perpendicular to the plane (zdirection),which ensures that the interaction between the periodic images of the sheet is negligible.The phonon calculations are carried out by using the Phonopy package with the forces calculated by the VASP code.[44]The edge states are calculated by the open-source software Wannier-tools package.[45]

Fig. 2. Atomic structures of (a) T-graphene, (b) T-graphene-1, (c) Tgraphene-2,and(d)T-graphene-3,with dashed lines showing primitive cells of all structures.

Table 1 presents optimized structural parameters,including lattice constants,bond lengths,space groups,and cohesive energy of the carbon networks from T-graphene to T-graphene-1, 2, 3. For comparison, the structural parameters of some other 2D carbon networks, such as Kagome graphene,[46]Tilene[47]are also given. To assess the stabilities of all structures,we calculate phonon spectra of the carbon allotropes as shown in Fig. S2. No soft phonon mode is found throughout the BZ,which indicates that all the structures are dynamic stable and they are all metastable structures.

Table 1. Space groups,lattice parameters,bond lengths,and cohesive energy(Ec)of carbon networks in Fig.2,and bond lengths between the atoms in triangular rings listed in brackets.

Next,the electronic properties of the carbon networks are explored. The calculation results indicate that all the structures possess flat bands and type-III Dirac points[see Figs.S3 in SI].It is noted that the type-III Dirac points in T-graphene-1,2,3 are located just around the Fermi level. Moreover,the Fermi surfaces of T-graphene-2, 3 are very clear, where only the energy bands related to the type-III Dirac points appear around the Fermi level[see Figs.4(a)and 4(c)]. Here,we use T-graphene-1, 2, 3 as example to explain the band structures of the carbon networks with diamond-like lattice.

The band structure of T-graphene-1 is given in Fig.3(a),

where a flat band crosses a dispersion band around the Fermi level along theΓ–Ypath, resulting in a type-III Dirac point.To clearly show the Dirac point, a 3D band structure around the Dirac point is given in the inset of Fig. 3(a), where the Dirac cone exhibits great anisotropy. To reveal the origination of the type-III Dirac point,in Fig.3(b)we plot charge densities of the quantum states corresponding to the points P1 and P2 in Fig. 3(a). One can find that the electrons on the state P1 are not localized while those on the P2 are localized on the carbon dimers. The localized quantum states are similar to the case of the flat-band state F1in Fig. 1(d). It means that the localized states in T-graphene-1 are also induced by the destructive interference.

Fig. 3. (a) Band structure of T-graphene-1, with inset showing 3D band structure around Dirac point denoted by dashed circle. (b)Charge densities for quantum states at points P1 and P2 in panel(a).

The band structures of T-graphene-2 and 3 are given in Figs. 4(a) and 4(c), respectively. There are flat bands and type-III Dirac points appearing around the Fermi level. Because there are no other bands crossing the Fermi level, the Fermi surfaces of the two structures are very clear. Moreover,there exist edge states between the type-III Dirac points in both structures [see Fig. S4]. Beside these type-III Dirac points,there is another type-III Dirac point at-2.0 eV along theΓ–Ypath in Fig. 4(a). The insets in Fig. 4(a) exhibit the 3D band structures of the two type-III Dirac points in T-graphene-2. To distinguish the two type-III Dirac points,the charge densities of the two quantum states at points P3 and P4 on the two flat bands are shown in Fig. 4(b). Comparing Fig. 4(b) with the insets in Fig.1(d),one can find that the localized states on the two flat bands in T-graphene-2 are corresponding to the quantum states F1and F2in Fig.1(d),respectively. Therefore,the two flat bands in Fig.4(a)are induced by different destructive interferences of wavefunctions. The type-III Dirac points in the carbon networks are very robust,whether a large uniaxial strain or a tensile/compressive strain cannot affect the flatness of the flat bands[see Fig.S5].

It is noted that there are also some other crossings at-0.5 eV between a flat band and other dispersive bands in Fig. 4(c). However, these crossings are not type-III Dirac points, instead they link together and form a nodal ring as shown in Fig. 4(d). The flat band at-0.5 eV is actually a flat plane,which originates from a localized state on a closed carbon ring[see the inset in Fig.4(c)].

In the 2D carbon networks in Fig. 2, T-graphene-1 has been synthesized experimentally.[48]Motivated by the successful synthesis, we propose that T-graphene-2 and Tgraphene-3 can also be synthesized by dehydrogenation chemical reactions of small molecules. For T-graphene-2, a 1-methylcyclopropane molecule[49]can serve as basic units as shown in Fig. 5(a), and two 1-methylcyclopropane molecules can be connected to a big molecule after dehydrogenation. Then, more big molecules form T-graphene-2 by self-assembly process. Similarly, one can usecis-1,2-dicyclopropylethene molecule[50]as a unit to construct unit cells of T-graphene-3,and then to obtain 2D carbon networks by self-assembly molecules[see Fig.5(b)].

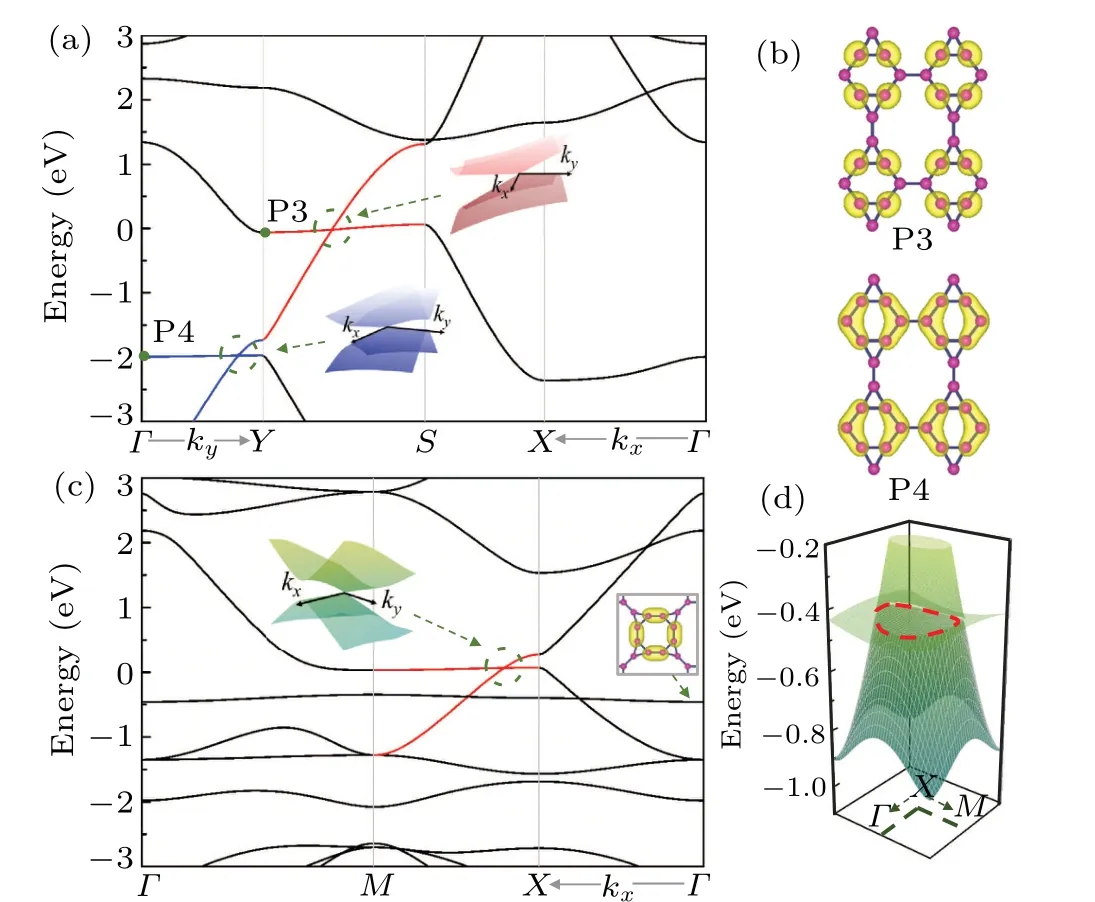
Fig.4.(a)Band structure of T-graphene-2 with inset showing 3D band structures around the Dirac points denoted by dashed circles.(b)Charge densities for quantum states at points P3 and P4 in panel (a). (c) Band structure of T-graphene-3, with left inset showing 3D band structure around the Dirac point denoted by dashed circles, and right inset referring to charge density of the quantum state on the flat band below the Fermi levels. (d) 3D band structure around high-symmetry point X in panel(c),with a red dotted circle denoting nodal ring.

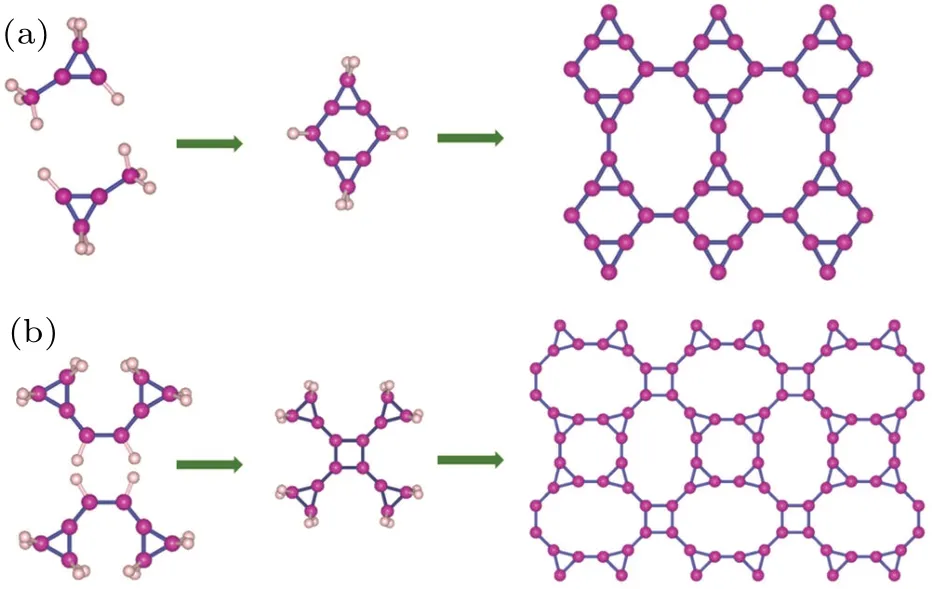
Fig.5. Possible routines to synthesize(a)T-graphene-2 and(b)T-graphene-3.

4. Discussion and conclusion

In this work, we proposed a kind of new lattice, named diamond-like lattice, which can produce intrinsic and robust type-III nodal points. The diamond-like lattice is a 2D version of diamond chain. A simulation based on a TB model indicates that three flat bands along high-symmetry lines appear on the band structure of the 2D lattice. When dispersive bands cross the flat bands, type-III nodal points form.Because the flat bands originate from localized states of destructive interference,they are protected by the lattice geometry. Thus,the flat bands and the corresponding type-III nodal points are very robust. A series of 2D single-layer carbon networks with diamond-like lattice are found,such as T-graphene and T-graphene-1,2,3. All the carbon structures possess type-III Dirac points. Especially, the type-III Dirac points in Tgraphene-2,3 are located just on the Fermi level,and the Fermi surfaces are very clear because no other energy bands crossing the Fermi level. The Dirac points are very robust against external strains. Besides the carbon networks mentioned above,we can find more 2D carbon networks possessing diamondlike lattices,and there are type-III Dirac points existing in the structure[see Fig.S6]. Considering that T-graphene-1 is synthesized successfully, we propose some possible experimental routines to synthesize T-graphene-2,3. These 2D carbon networks provide a good platform for studying the diamondlike lattice and corresponding type-III Dirac points. Our research not only opens the door to finding the ideal type-III Dirac points, but also provides materials for exploring their physical properties experimentally.

Acknowledgement

Project supported by the National Natural Science Foundation of China (Grant Nos. 12174157, 12074150, and 11874314).