M型多技能客服中心排队信息提示问题研究

李春艳

(浙江金融职业学院，浙江 杭州 310012)

0 引言

客服中心即呼叫中心，是为了客户服务、市场营销、技术支持和其他的特定商业活动而接收和发出呼叫的一个实体。随着信息化大数据时代的到来，呼叫中心与人们的日常生活息息相关。排队信息提示是呼叫中心的一种新型的运营模式，它是指呼叫中心通过语音提示的方式告知顾客估计需要等待的时间。对于看不见队列的服务系统，如呼叫中心服务系统，告知顾客需要等待的排队时间具有特殊的作用。在这类队列不可见的服务系统中，等待时引起的不耐烦情绪要比队列可见的系统高很多。这种不耐烦并不会随着时间慢慢减少。顾客没有办法估计队列的长度或进展程度。不耐烦、焦虑等情绪会随着等待时间延长而不断增长。为顾客提供排队信息提示，可以大大避免这些情况出现，使得等待的过程可以被顾客接受。排队信息提示对顾客的等待心理有很大的影响，可以提高顾客的满意度。本文对带有排队信息提示的M型多技能呼叫中心进行研究，给出排队等待时间的计算方法。

在早期关于呼叫中心的研究中，人们通常认为所有的来电都没有差别，客服人员也都拥有同样的技能，每个客服都可以处理所有的电话，这样的呼叫中心被称为单技能呼叫中心。近年来，随着呼叫中心的快速发展，呼叫中心逐渐大型化，多技能呼叫中心越来越多。在多技能呼叫中心中，呼入电话分为不同类型，客服人员也可以拥有各种不同的技能，即客服人员可以只拥有一种技能也可以同时拥有几种不同的技能。多技能概念的引入，使得呼叫中心的运营以及评估变得复杂。呼叫中心技能的复杂化使得原来支撑单技能呼叫中心运营服务水平计算的理论无法继续在多技能的呼叫中心中应用。因此，多技能呼叫中心的研究受到了越来越多的关注。关于排队信息提示问题，Ibrahim和Whitt[1]研究了带有时变到达率的多服务员排队系统的延迟预测问题。其中，服务员数目是时变的，且顾客可以放弃排队。接下来更进一步的研究是通知预测的延迟时间，Whitt[2]研究了通知延迟对单技能呼叫中心性能的影响。Jouini等[3-4]进一步研究了后面的一些相关工作，他的研究方法是基于排队分析的，还有一种不同的研究方法是基于流模型的。Armony等[5]利用这种方法研究了延迟信息对多服务员排队的影响。于淼等[6]考虑了单技能呼叫中心等待提示策略的呼叫中心流体近似方法。Jouini等[7]研究了一个近似M(t)/M/s(t)的呼叫中心排队模型，用Erlang分布来近似延迟分布，提出了两种延迟估计并用仿真方法进行了验证。以上文献都是研究的传统的单技能呼叫中心。本文进一步拓展，研究多技能呼叫中心的排队信息提示问题。本文的研究丰富了对于考虑顾客等待心理的提示等待呼叫系统的研究内容，构建了更加符合现实呼叫中心多种电话呼入、多种技能服务员的呼叫排队系统，可以为呼叫中心的管理者对呼叫系统进行合理管理与决策提供有价值的参考策略。

1 模型描述

在实际的呼叫中心系统中，大多数具有两种类型的顾客，比如双语呼叫中心，有中文呼入和外文呼入两种类型的呼入电话。这就要求客服人员同时掌握中英文两种语言，但这样的客服人员成本相对较高。因此，呼叫中心只有部分客服是掌握两种语言的，其他一部分只会中文，另一部分只会英文。客服人员有3组，一组拥有两种技能，另两组则分别拥有一种技能。本文研究的是一个带有排队信息提示的多技能M型呼叫中心，系统有两种类型的电话呼入，这两种电话的到达是互相独立的，且分别服从到达率为λ1和μ3的泊松过程。同时，系统有3类客服组，分别拥有不同的技能，其中客服组1只能为电话1服务，服务时间服从指数分布服务率为μ1，拥有客服人数为N1。客服组2只能为电话2服务，服务时间服从指数分布服务率为μ2，拥有客服人数为N2。客服组3既可以为电话1服务，也可以为电话2服务，服务时间也服从指数分布服务率为μ3，客服人数为N3。假设同一客服组对不同电话类型的服务率是相同的，同时假设被接听的电话都能够被一次性满意服务，即不会出现电话在不同的客服之间转接的情况。

本模型的路由政策是基于技能的路由，不考虑2种不同类型呼叫的重要性。即当呼叫到达时，电话1(或2)毫无疑问首先被分配给客服组1(或2)服务，而当客服组1(或2)全部忙碌时则选择客服组3服务，若客服组3也全部忙碌，则进入队列1(或2)排队等待。当客服结束服务时，客服组1(或2)选择电话1(或2)进行服务，而对于客服组3，当电话1和电话2都排队时，则以1/2的概率随机选择电话1或者电话2进行服务。2种类型电话的队列是相互独立的。假设排队空间无限，即电话不会因为排队空间不够而被系统放弃。对于同一类型的电话都是先到先服务。

本模型不考虑顾客的不耐烦特性，因此对顾客进行排队信息提示对原始模型不会有影响，所以是否通知顾客需要等待的排队时间，对系统的性能指标没有影响，但是告知顾客需要等待的时间，可以大大减少顾客等待过程中的不确定性，从而提高顾客的满意度。

2 顾客排队等待时间的计算

本系统考虑一个新的呼叫到达系统时，有两种可能的情况，一是系统中还有可以为它服务的服务员空闲，则这个新的呼叫将立刻得到服务，不需要等待。因此，系统不需要为它提供任何等待信息。另外一种情况是当呼叫到达时，系统可以提供服务的服务员都处于忙碌状态，则它必须在队列中等待服务，系统会对其进行排队信息提示，告知需要等待的时间。

同样，用系统中顾客的数目来定义系统的状态，设n1表示新到达的电话1所看到的队列1中电话1的数目，n2表示新到达的电话2所看到的队列2中电话2的数目，同时设nT=n1+n2表示系统队列1和队列2中总共的排队人数。具体模型如图1所示，其中队列1中有n1人，队列2中有n2人。

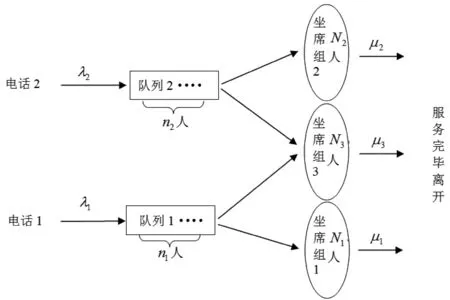
图1 顾客耐心无限的M型呼叫中心排队模型

下面计算电话1和电话2的平均等待时间，假设系统服务员处于忙碌状态，且nT=n1+n2≥0，有电话在队列中等待。这里将电话1的等待时间和电话2的等待时间分开进行研究。

2.1 电话1等待时间的计算

假设有一个新到达的电话1进入系统，此时系统中电话1排队，队列1中有n1个电话，电话2也排队，队列2中有n2个电话。由于本模型路由策略的设置，当客服组1的服务员都处于忙碌状态时，客服组3的服务员也可以为电话1服务，此时出现两个客服组同时为电话1服务的情况。客服组1拥有N1个服务员，服务率μ1，客服组3拥有N3个服务员，服务率μ3。客服组3以1/2的概率为电话1服务。新到的电话1在队列中等待的时间与电话2排队等待的数目无关，同样也与后面到达的电话1无关，系统采取先到先服务的策略。

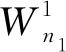
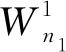
(1)

分布函数为：

(2)

平均等待时间为：

(3)

方差：

(4)

2.2 电话2等待时间的计算

对于电话2的等待时间计算方法和电话1是一样的。假设有一个新到达的电话2进入系统，此时系统中电话1排队，队列1中有n1个电话，电话2也排队，队列2中有n2个电话，则这个电话2进入服务前，需要等待n2个电话都被服务完，且有一个电话2刚好服务完，这个电话2才能接受服务。当客服组2的服务员都处于忙碌状态时，客服组3的服务员也可以为电话2服务，此时出现两个客服组同时为电话2服务的情况。客服组2拥有N2个服务员，服务率μ2，客服组3拥有N3个服务员，服务率μ3，客服组3以1/2的概率为电话2服务。新到的电话2在队列中等待的时间与电话1排队等待的数目无关，同样也与后面到达的电话2无关，系统采取先到先服务的策略。

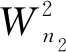
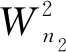
(5)

分布函数为：

(6)

平均等待时间为：

(7)

3 结语

本文研究了顾客耐心无限的M型多技能呼叫中心模型，系统有两种类型的电话呼入，同时有3个拥有不同技能的客服组。笔者利用排队模型，分析了当系统内队列1和队列2都排队，再到达1个电话1时，其所需要的平均等待时间的计算公式和再到达1个电话2时，其所需要的平均等待时间的计算公式。此算法可以为实际呼叫中心的排队时间计算问题提供一定的参考。