基于自动加权法的扩展卡尔曼滤波数据融合算法研究

尹建军，陈 涛，岳海燕

(零八一电子集团有限公司，四川 成都 611731)

1 研究背景及意义

随着现代信息科技不断地进步与发展，单部雷达所面临的威胁越来越大。战斗过程中使用压制性电子干扰手段使雷达迷盲，性能将大大减低或者完全失效。在此背景下，雷达组网系统应运而生。雷达组网系统极大地扩展了在空间和频域上雷达系统探测区域的覆盖范围，改善了单部雷达不能充分利用探测信息的问题，提高了整个系统的工作效率以及抗干扰能力。雷达组网系统不是单纯的完成数据拼凑，而是将不同体制、不同频率的数据融合成更为精确的数据，从而提高系统对目标的跟踪精度综合探测能力[1]。但是在实际情况中，雷达组网系统中雷达的探测精度、探测范围均不同，同时探测精度还会受外界环境因素的影响。在某些情况下，数据融合后的数据精度反而更差。因此如何提高数据融合精度是当前急需解决的关键问题。目前常用的数据融合算法包括卡尔曼滤波(Kalman Filter,KF)算法、粒子(Particle Filter,PF)算法等。滤波状态方程均在直角坐标系下建立的，但雷达测量数据多为极坐标系，两者是非线性关系，因而在实际应用情况中线性卡尔曼滤波受到的一定的限制。非线性卡尔曼滤波算法应运而生，目前扩展卡尔曼滤波器(Extended Kalman Filter,EKF)是应用最为广泛的非线性滤波器。扩展卡尔曼滤波器虽然解决了非线性系统的滤波问题，但其实质是将非线性系统转换为局部线性系统来进行估计，滤波结果存在一定的误差。同时扩展卡尔曼滤波器实际的估计误差超过理论预计值时，滤波器出现发散现象，导致算法精度变差。

本文主要研究如何解决雷达组网系统数据融合扩展卡尔曼滤波器发散的问题。笔者主要考虑在非线性滤波器中，结合扩展卡尔曼滤波算法的特点，通过自动加权的方法对扩展卡尔曼滤波器的发散问题进行判断，完成扩展卡尔曼滤波器算法的修正，提高数据融合算法精度，从而更好地完成雷达组网系统中的数据融合功能。首先给出标准的扩展卡尔曼滤波数据融合算法的基本流程，在此基础上提出使用自动加权法判断滤波器的发散情况,然后根据判断结果进行相应的处理。

2 雷达组网系统概述

雷达组网系统通过将多部雷达适当优化部署，通过有效的通讯方式链接各雷达与数据融合处理中心。各雷达与数据融合中心组成一个完整的网络系统。雷达组网系统内，数据融合处理中心与各雷达形成网状结构。数据融合中心接收各雷达探测的目标数据，通过数据融合处理获得更为精确的目标数据，从而高效准确地完成目标的探测、定位、跟踪任务[2]。

网内各雷达均在本地由独立的数据处理器，各雷达监测到目标后先对目标进行跟踪与状态估计，在航迹起始后生成对应目标的稳定的航迹，最后将目标的航迹信息发送至数据融合处理中心。数据融合处理中心对接收到的各雷达的航迹数据进行坐标转换，误差配准、航迹关联、航迹融合等处理，最终形成目标的融合航迹[3]。

3 航迹融合扩展卡尔曼滤波流程

雷达组网系统数据融合处理中心接收到新的观测数据就对其进行相关处理。判断新观测数据是否与航迹相关，完成点迹与航迹的融合。

卡尔曼滤波：卡尔曼滤波系统模型—采用状态变量法描述动态系统，卡尔曼滤波系统的状态方程描述，即

xk+1=Φkxk+Bkuk+Gvk

(1)

系统的量测方程为：

zk=Hkxk+Lkwk

(2)

式中xk+1表示k+1时刻运动目标的状态向量，zk+1表示k+1时刻的观测向量，vk是零均值、白色高斯过程噪声矩阵，其协方差为Qk；wk是零均值、白色高斯量测噪声矩阵，其协方差为Rk；Hk是观测矩阵，它反映观测矢量是某些状态变量的线性组合。Qk和Rk两者互不相关。Φ表示运动过程状态向量的转移矩阵。

卡尔曼滤波方程，卡尔曼滤波状态更新方程：

(3)

协方差更新方程：

Pk+1/k+1=[I-Kk+1Hk+1]Pk+1/k

(4)

协方差矩阵的预测：

(5)

卡尔曼滤波增益：

(6)

式中P表示状态协方差矩阵；K表示滤波器的增益矩阵，S表示滤波器的新息协方差矩阵[4]。

根据第一时刻和第二时刻的量测值进行卡尔曼滤波初始化，求取滤波的初始状态X(0)和初始协方差P(0)，从而开始卡尔曼滤波航迹的滤波和外推。

往往实际情况下，在雷达组网系统中的数据融合处理中心获得的观测数据(距离、方位、俯仰)与目标动态参数间的关系都是非线性的。扩展卡尔曼滤波如下。

扩展卡尔曼滤波模型，所描述的离散时间非线性过程的模型为：

xk+1=fk(xk)+vk

(7)

而观测方程为：

zk+1=hk+1(xk+1)+wk+1

(8)

式中，非线性函数f(·)为动态模型函数。非线性函数h(·)是量测模型函数。

扩展卡尔曼滤波线性化处理：扩展卡尔曼滤波将非线性问题转化成一个近似的线性问题处理，线性化方法处理方法如下：将非线性函数f(·)、g(·)和h(·)进行泰勒级数展开，只保留泰勒级数展开式的低次项[5]。

计算系统状态方程的状态转移矩阵：

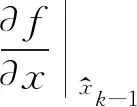
(9)

在进行线性化以后，计算状态估计值和估计误差协方差：

状态估计值：

(10)

估计误差协方差：

(11)

测量矩阵：

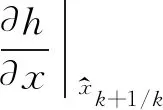
(12)

对应的在直角坐标系中，滤波使用的新息协方差矩阵、权增益矩阵为

(13)

(14)

而坐标间的非线性变换为

z=h(x)

(15)

滤波状态估计值：

(16)

而测量误差的协方差为Rk+1。式中的估计误差协方差为

Pk+1=[I-Kk+1Hk+1]Pk+1/k

(17)

扩展卡尔曼滤波相比于其他的非线性滤波算法，优点是使用较为方便。但是在实际应用中，线性化解决非线性系统所产生的截断误差对目标状态估计结果影响明显，严重时导致滤波器发散。

4 自动加权法

由于滤波产生发散的直接原因是实际估计误差超过理论预计值，因新息中包含了实际估计误差的新息，可通过自动加权的方法判断出滤波器是否发散。

判断滤波器发散依据：

(18)

(19)

(20)

γ=1,严格收敛条件：

(21)

在扩展卡尔曼滤波算法处理过程中，通过自动加权法判断出滤波器发散时，对滤波器进行初始化，重新进行计算迭代，从而更好地拟制卡尔曼滤波器的发散。

基于自动加权法的扩展卡尔曼滤波数据融合算法流程如图1所示。

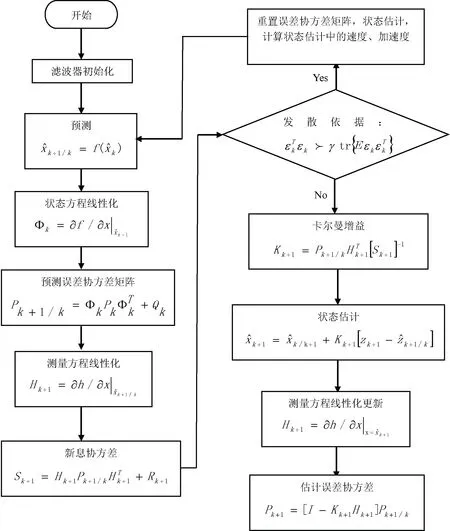
图1 基于自动加权法的扩展卡尔曼滤波数据融合算法流程

5 结语

针对雷达组网系统中数据融合的非线性系统的滤波问题，结合扩展卡尔曼滤波器算法自身的特点，利用自动加权法对扩展卡尔曼滤波器进行发散的情况进行监控。判断出滤波器发散后，重新设置误差协方差矩阵，以及状态估计值，修正滤波器参数，继续完成跟踪滤波，提高雷达组网系统数据融合的精度。笔者通过航迹模拟器生成多雷达航迹，使用该算法对航迹进行数据融合。实践结果表明，该方法能够很好地拟制扩展卡尔曼滤波器的发散，修正滤波器，能够更好地适应非线性滤波。本文所提的基于自动加权法的扩展卡尔曼滤波思想可以进一步地使用到其他应用和研究工作中。