基于ADRC的电力巡检多旋翼无人机姿态控制研究

张恺嘉，杨瑞峰，郭开阳，侯 杰

(1.国网山西省电力公司繁峙县供电公司，山西 繁峙 034300；2.国网山西省电力公司忻州供电公司,山西 忻州 034099)

0 引言

电力输送是电力工业重要的环节之一，而电力巡检是确保电网线路可靠、稳定运行的重要基础。近年来，多旋翼无人机凭借更低的成本和更高的效率，在电力巡检领域被广泛应用。多旋翼无人机可通过搭载高清摄像机和热成像议等设备，及时准确地采集各种输电线路信息，同时借助5G技术将信息实时传回地面操作站，帮助巡检人员进行故障排查、排除等工作。

在实施电力巡检的过程中，尤其是在地形地势较差的山区中开展电力作业，大风等诸多不利因素往往会给无人机的控制带来困难。因此，在电力巡检领域多旋翼无人机的姿态控制技术研究显得尤为重要。

多旋翼无人机控制存在着强耦合性、非线性、参数时变性以及其他内部不确定因素和外部扰动作用等特点[1]。因此，传统的PID控制器在多旋翼无人机控制问题上有一定局限性，控制效果往往差强人意。为解决电力巡检无人机姿态的控制问题，本文以四旋翼无人机为研究对象，通过自抗扰控制技术(Auto/Active Disturbances Rejection Controler， ADRC)将四旋翼无人机多种不确定性因素归结为总扰动[2]，利用非线性控制技术解决四旋翼无人机姿态的控制难题。

1 自抗扰控制器(ADRC)

自抗扰控制技术(ADRC)是由韩京清教授于1998年提出的一种补偿控制方法，通过模型预估系统受到的内部扰动和外部扰动之和，进而获得自抗扰控制算法的补偿量，实现系统的控制目标。该控制技术最大的优势在于控制系统内的扩张观测器可以实时在线地预估系统受到的扰动量，极大地提升了算法控制的实时性和准确性。自抗扰控制系统包括3个基本模块[3]，其一是跟踪微分器(Tracking Differentiator， TD)，其主要作用是滤除输入信号的噪声并提取微分信号，同时可以控制信号变化的平稳性；其二是扩展观测器(Extended State Observer， ESO)，其主要作用是对系统受到的外部扰动和内部扰动进行观测，并且该观测是实时进行的；其三是非线性状态误差反馈控制(Nonlinear State Error Feedback， NLSEF)，其主要作用是帮助系统找到合适的误差信号组合方式，保证系统的控制准确和提升系统控制的效率。自抗扰控制器的详细结构如图1所示。

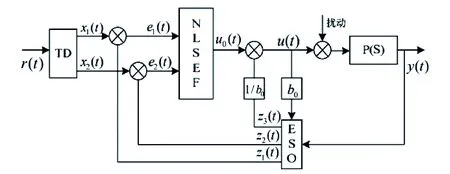
图1 自抗扰控制器的详细结构

2 四旋翼无人机模型

四旋翼无人机运动示意如图2所示。建立四旋翼无人机定坐标系O-Xb，Yb，Zb和动坐标系E-Xa，Ya，Za。其中，Φ、θ、Ψ分别为四旋翼无人机的滚转角、俯仰角、偏航角；Ω为无人机电机转速；U为无人机控制量；l为无人机重心到旋翼距离；Jr为无人机的旋翼转动惯量；b为无人机升力系数；d为无人机阻力系数；Ix，Iy，Iz为无人机转动惯量。

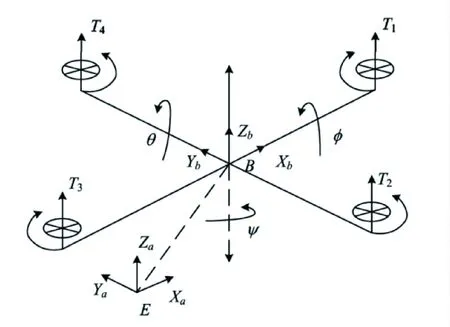
图2 四旋翼无人机运动示意

四旋翼无人机定坐标系和动坐标系的转换关系如下式(1)所示。

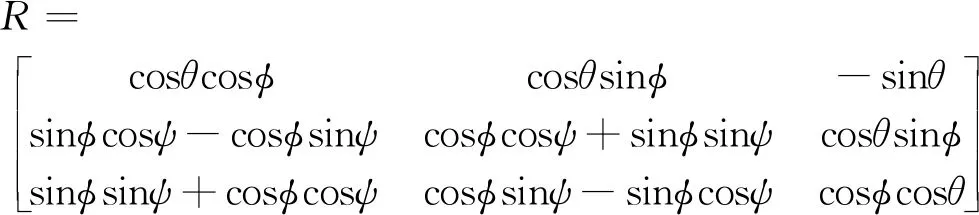
(1)

为建立四旋翼无人机运动模型，现对无人机系统做如下假设：(1)假设四旋翼无人机为刚体，外界干扰不会影响无人机的结构；(2)四旋翼无人机重力加速度及其变化和空气阻力等外界干扰不会影响无人机系统[4]。基于上述假设并借助牛顿-欧拉法建立四旋翼无人机运动模型[5]，如式(2)所示。

(2)

各自由度之间的控制量和转速之间的关系如式(3)所示。

(3)

3 基于ADRC的姿态控制

对四旋翼无人机运动模型式(2)进行分析，四旋翼无人机姿态控制中滚转角、俯仰角及偏航角和位置控制中的高度变量之间存在强耦合，其中任意一个变量发生变化，其余变量所在的控制通道都会被影响，严重时四旋翼无人机甚至发生不可控事件。前文提到自抗扰算法正好可以处理四旋翼无人机姿态控制中的各回路相互耦合问题。

针对以上4个变量参数，如俯仰角的控制，当俯仰角通道参数数值变化，利用自抗扰算法进行四旋翼无人机姿态控制时，可将高度和其他2个姿态参数的预期偏差视为系统内部扰动，同时考虑到系统存在的多种多样的外部扰动，自抗扰系统中扩张观测器会自动将外部扰动和内部扰动整合并自动进行实时的预估，最后将扩张观测器的预估值与给定俯仰角值目标值的差值进行补偿，最终控制系统将达到俯仰角给定的目标值。

通过以上俯仰角采用ADRC算法控制的分析，在实际四旋翼无人机的控制中存在3个姿态角变量和1个位置高度变量，针对这4个变量采用4个ADRC控制器分别对各变量进行控制。按照此设计思路得到四旋翼无人机基于ADRC的姿态控制系统结构，如图3所示。

图3 四旋翼无人机基于ADRC的姿态控制系统结构

4 系统仿真

4.1 ADRC控制器设计

针对本文设计的四旋翼无人机基于ADRC的姿态控制器模型，本节拟在Matlab的Simulink环境下进行实验仿真。实验仿真可充分对本文设计控制器的可靠性和有效性进行验证。上文得到的四旋翼无人机运动模型，详见式(2)。本节设计了一个最基本的自动控制闭环系统开展实验，如图4所示的基于ADRC控制器四旋翼无人控制仿真模型[5]。本节中的四旋翼无人机运动模型和自抗扰控制器模型中的模块选用S-function进行设计，这样可以大幅提升验证实验的方便性。

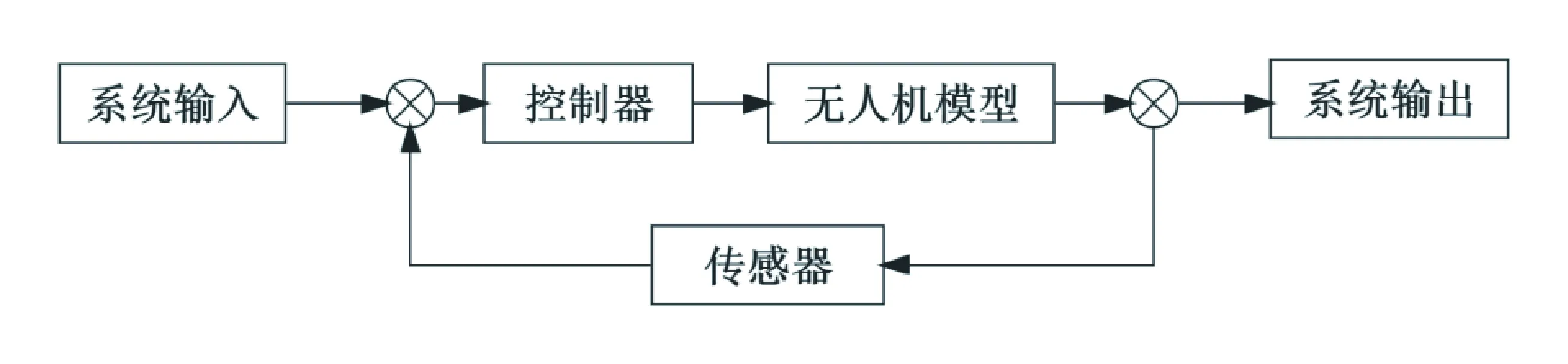
图4 基于ADRC控制器四旋翼无人控制仿真模型

本节验证实验中，四旋翼无人机运动模型的参数设置如表1所示。

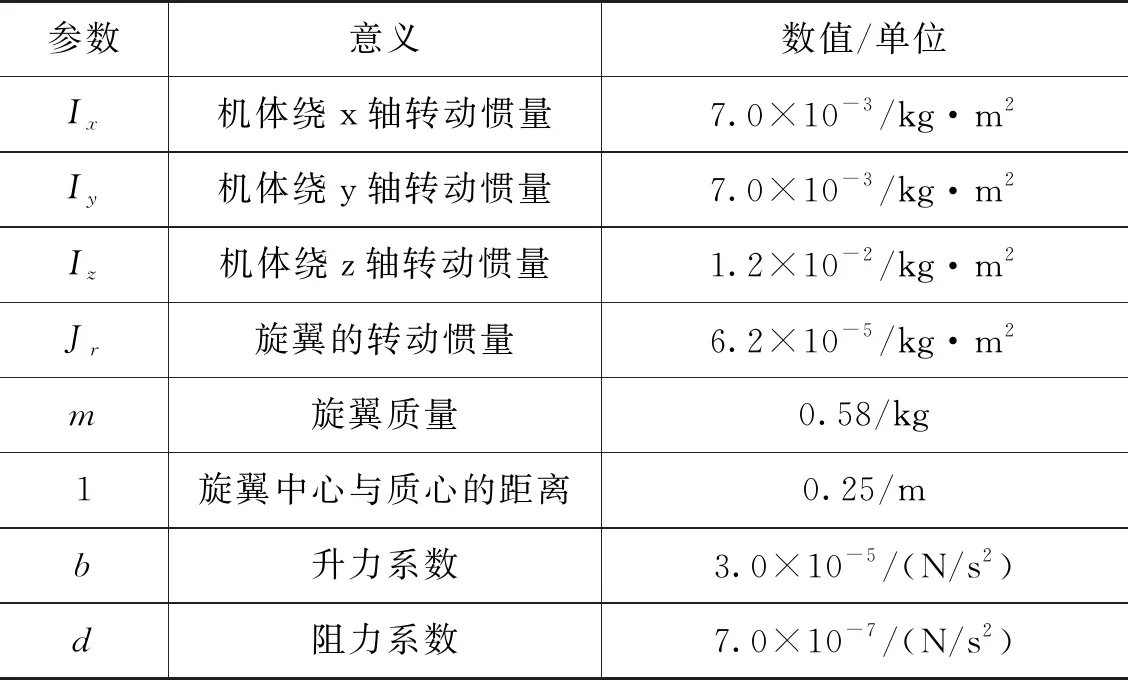
表1 四旋翼无人机运动模型参数

本节四旋翼无人机Matlab仿真实验中，高度、滚转角、俯仰角及偏航角四路ADRC控制器的设计参数取值如表2所示。自抗扰控制算法的参数整定结合了算法自身的整定原则和实际仿真结果[5]。

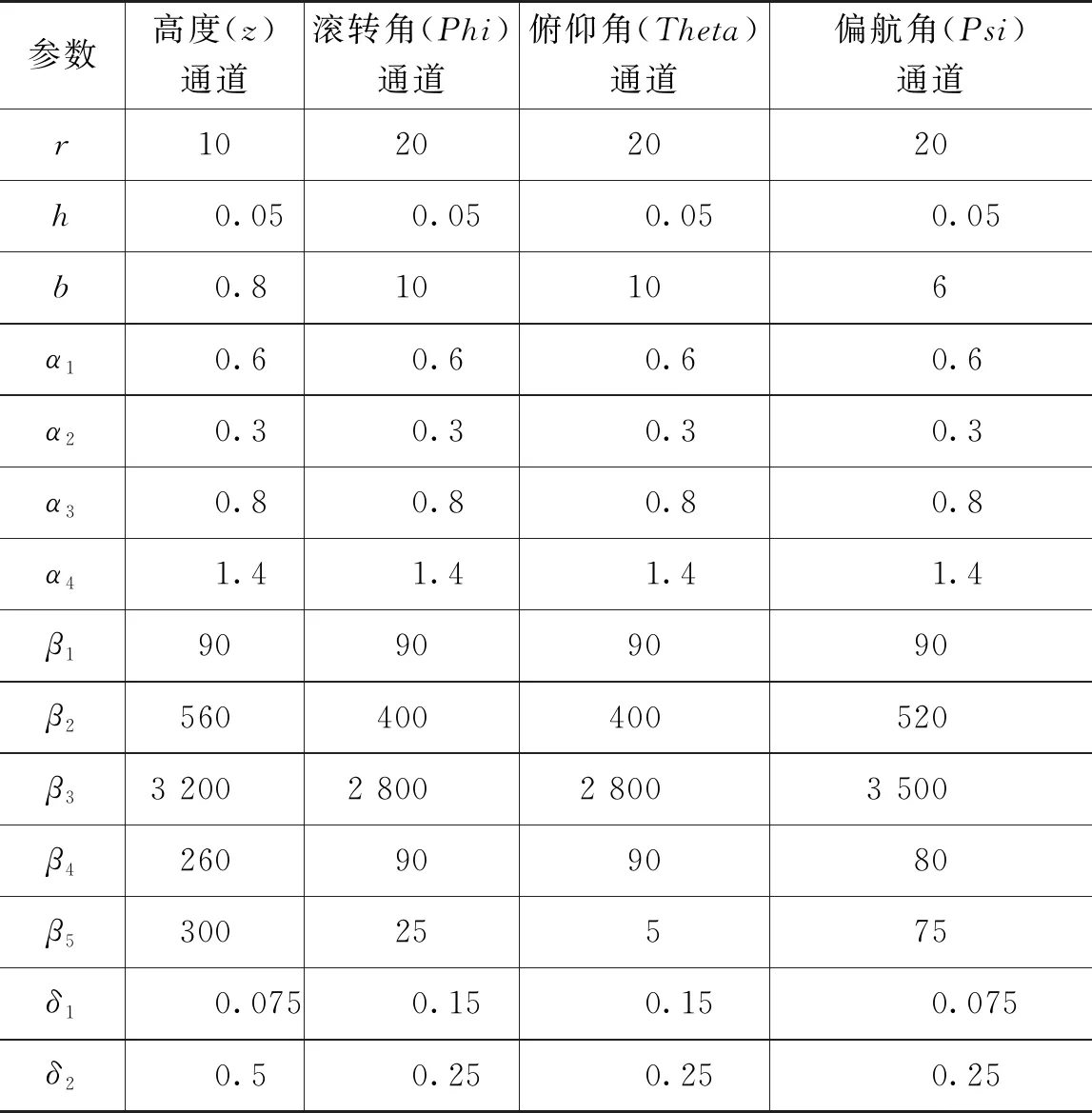
表2 四路ADRC控制器参数

4.2 ADRC控制器仿真结果

在进行四旋翼无人机仿真实验时，假定四旋翼无人机初始位置为0点，坐标为(0，0，0)。同时，该处是大地坐标的原点和无人机机体坐标的原点[6]。在本节进行的验证实验中，预设四旋翼无人的控制位置高度目标值为3 m，同时设定四旋翼无人机3 m悬停高度时的滚转角目标值为5°、俯仰角目标值为9°及偏航角目标值为7°。在Matlab中，设置系统仿真步长、实验时长分别为0.01 s和10 s。系统仿真实验结果如图5、图6、图7和图8所示。

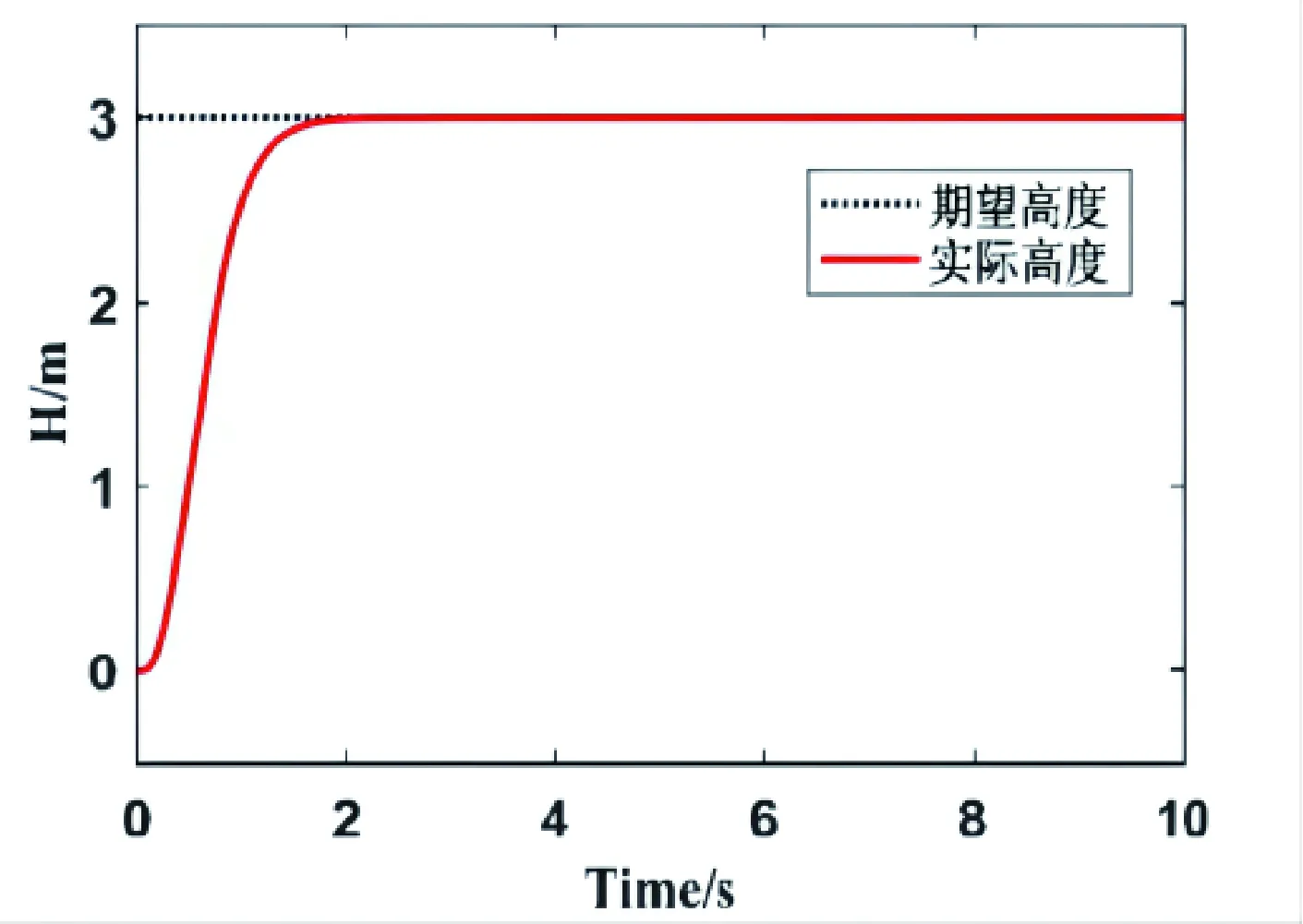
图5 四旋翼无人机高度悬停控制实验结果

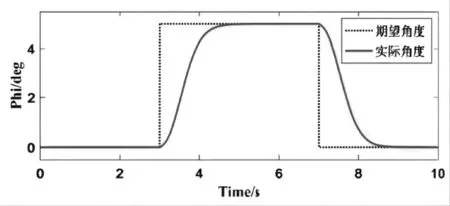
图6 四旋翼无人机滚转角控制实验结果

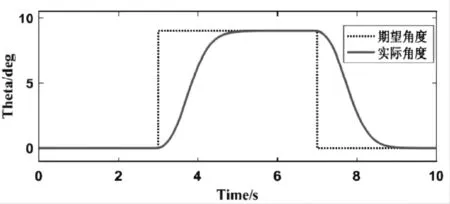
图7 四旋翼无人机俯仰角控制实验结果

图8 四旋翼无人机偏航角控制实验结果

从上述仿真结果可以看出，若四旋翼无人机在无外界干扰时，基于自抗扰控制算法的无人机控制系统可以很好地实现无人机姿态和高度的控制目标。四旋翼无人机ADRC控制器的姿态控制各变量的调整时间如表3所示。

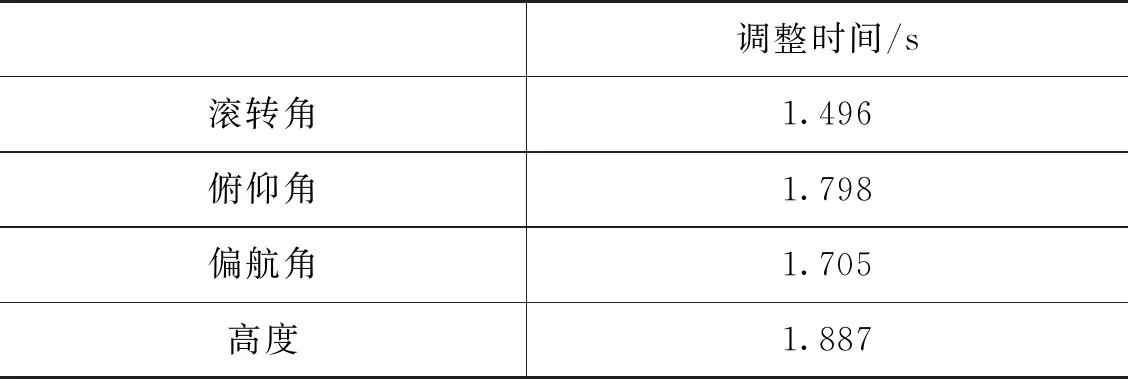
表3 四旋翼无人机ADRC控制器姿态控制变量的调整时间

从表3可以看出，四旋翼无人机的位置高度悬停、姿态滚转角、俯仰角及偏航角的控制目标实现时间基本在2 s内均可实现。同时，各控制通道的控制目标超调量与稳态误差均为0。自抗扰控制算法在四旋翼无人机的位置高度、姿态滚转角、俯仰角及偏航角控制中平稳性和快速性均效果良好。

5 结语

本文主要针对多旋翼无人机在电力巡检过程中，利用ADRC算法解决位置和姿态控制问题。文章分析了ADRC控制算法的3个基本组成部分的特性，分别是非线性状态误差反馈控制器、扩展观测器及跟踪微分器；建立了四旋翼无人机的运动模型，并给出了各自由度之间的控制量和转速之间的关系式。在此基础上，本文对四旋翼无人机高度和各姿态角通道分别使用ADRC算法单独控制，设计了基于ADRC算法的四旋翼无人机控制系统。本设计针对设计的控制系统进行仿真实验，在Matlab中搭建了控制结构、选取了合适的四旋翼无人机模型参数和ADRC算法参数，进行了基于ADRC控制算法的四旋翼无人机位置高度和姿态仿真实验，实验结果达到预期目标，实验算法控制效果良好。