区域内不同层次轨道交通末班车时刻表协同优化
2022-11-21胡勇健郑俊锋
胡勇健 郑俊锋 李 莉
(合肥市轨道交通集团有限公司,230601,合肥∥第一作者,高级工程师)
0 引言
规划建设干线铁路、城际铁路、市域(郊)铁路和城市轨道交通的多层次轨道交通、推进“四网融合”发展,是推进国家新型城镇化战略实施,促进城市群、都市圈一体化发展的重要举措。目前,我国多层次轨道交通仍然面临功能分工不合理、网络布局不完善、枢纽衔接不顺畅等现实问题。接续优化不同层次轨道交通在“四网”枢纽换乘站和线间换乘站的末班车时刻表,是提高多层次轨道交通网络时效性与可达性的重要途径。本文研究不同层次轨道交通末班车时刻表协同优化,主要是通过调整末班车的始发站发车时间与换乘站到达时间,实现不同线路末班车时刻表协同优化,实现区域OD(起讫点)可达。
单一层次轨道交通(如城市轨道交通)时刻表的既有研究已较为完善,其大致将末班车时刻表协同优化目标分为乘客换乘量最大和网络可达性最大两类。文献[1]以区域 OD 可达客流比例最大和各线路收车延时最小为目标,以列车开行间隔及停站时分为约束,构建了双目标优化模型。文献[2-3]基于Logit模型计算乘客路径选择概率,以时空可达性为目标,构建了双层规划模型。文献[4]基于线网拓扑网络构建复杂度计算指标,实现末班车协同优化。文献[5]通过遗传算法,通过调整列车发车间隔及停站间隔等减少乘客换乘等待时间。文献[6]参考城市轨道交通末班车时刻表优化方法,实现了公交车末班车时刻表协同优化。
城市轨道交通末班车时刻表协同优化问题常以滞留乘客数量最小为目标,但末班车时段OD间不同路径存在可行性差异,因此乘客的路径选择将直接影响末班车时段乘客滞留数量。而乘客面对多层次轨道交通网络和单一层次轨道交通网络时,其路径选择行为存在差异:在单一层次轨道交通网络中,乘客仅以出行总时间最小为目标;而在多层次轨道交通网络中,乘客的出行路径涉及不同层次轨道交通间的换乘,除考虑出行时间最小外,乘客还会考虑换乘的复杂度及困难度。本文分别以乘客路径总的轨道交通复杂度及不同层次轨道交通间收车延时值差异对其进行量化,通过MML模型计算乘客选择OD间不同路径的概率,使多层次轨道交通末班车时刻表协同优化到达一定程度,以增强长距离出行客流需求的匹配度。
本文设计了算法来分析、判断区域OD可达性,从区域OD可达性和运营部门成本出发,构建多目标优化模型,以实现不同层次轨道交通末班车时刻表协同优化。
1 不同层次轨道交通末班车时刻表协同优化问题描述
不同层次轨道交通末班车时刻表协同优化问题可分为2个子问题:区域OD可达性判别问题和末班车时刻表协同优化问题。前者为评价后者质量的重要指标,后者为乘客需求及运营部门效益的集中体现。
区域OD可达与否取决于乘客换乘过程中的冗余时间,如图1所示。若换乘冗余时间大于或等于零,则该次换乘可行。若乘客选择路径中不存在换乘不可行状态,则判断OD可达;反之,则不可达。
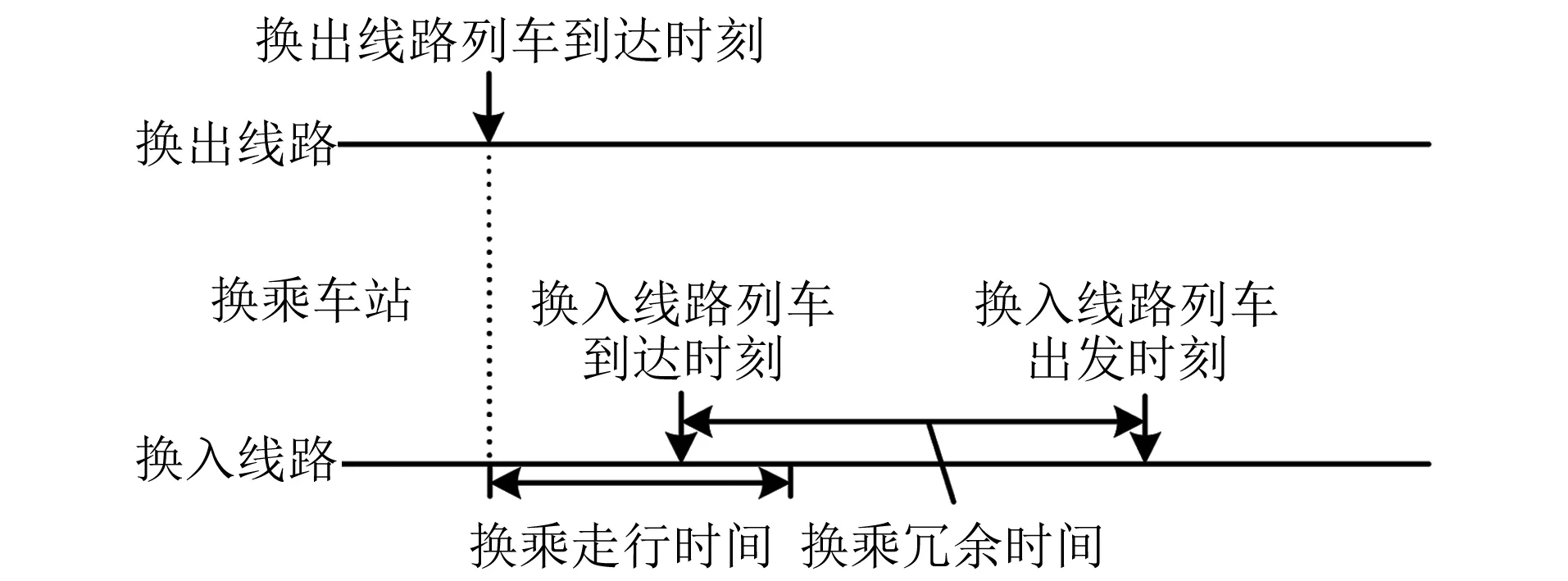
图1 换乘冗余时间示意图Fig.1 Diagram of transfer redundancy time
单一层次轨道交通网络OD间常存在多条可行路径,当最佳路径因线路收车而失效后,乘客亦可选择替代方案完成出行。如图2所示,OD间同时包含O—H1—H2—H4—D和O—H1—H3—H4—D(H代表换乘站)两条可行路径,当其中一条路径因收车失效后,乘客可选择另一条路径。多层次轨道交通网络OD间会存在更多可行路径,然而随着乘客出行路径涉及的交通方式和线路的增多,使线路换乘和收车信息愈加复杂。如图3所示,图中空心点为不同层次轨道交通间的换乘点;其OD间途经3种交通方式,可行路径有9条,包含不同层次轨道交通间的5个换乘点,乘客难以在出行路径失效时选择当前状态的最佳替代方案。
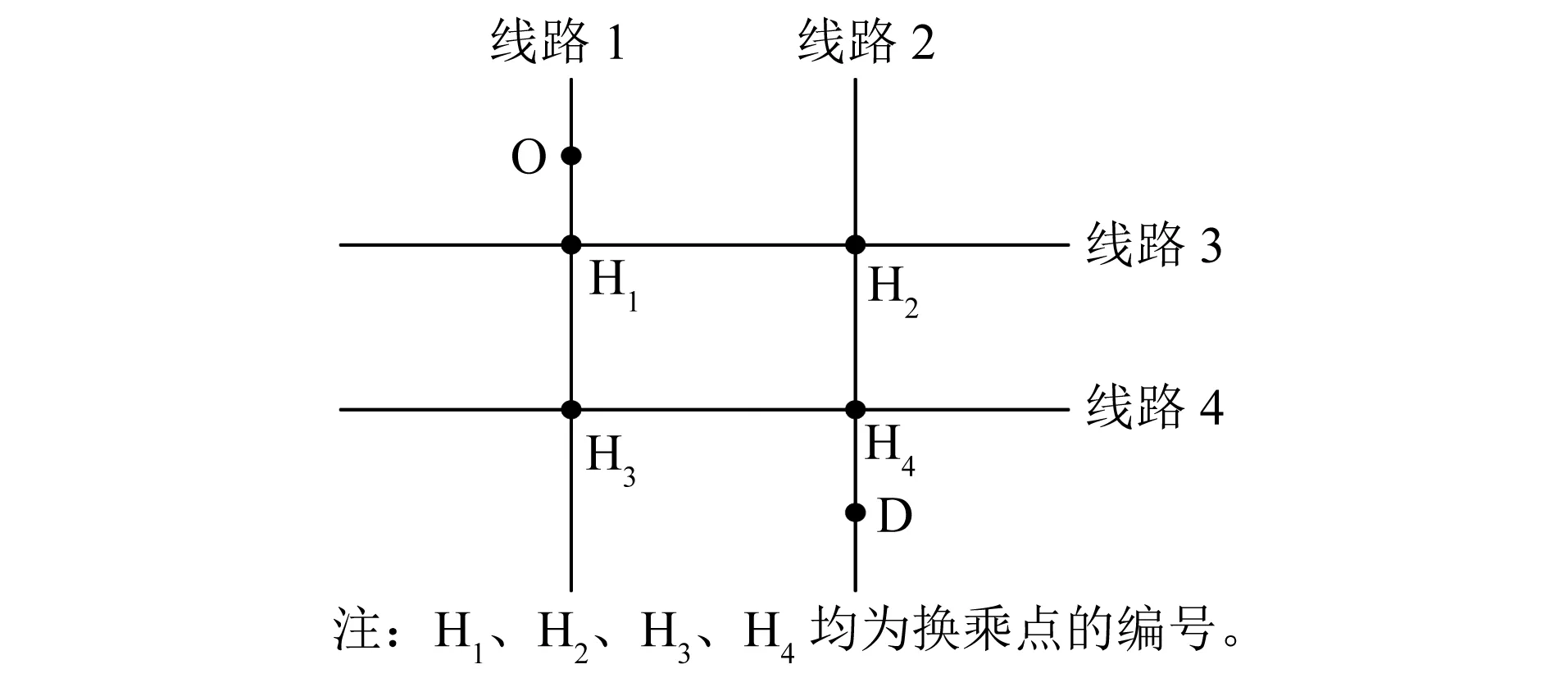
图2 单一层次轨道交通网络换乘示意图Fig.2 Diagram of single-level rail transit network interchange

图3 多层次轨道交通网络换乘示意图Fig.3 Diagram of multi-level rail transit network interchange
2 不同层次轨道交通末班车时刻表协同优化数学模型
2.1 模型假设
为简化模型,增加求解效率,本文多模型做出以下假设:① 列车区间运行时分、停站时分、间隔时间恒定;② 末班车时段内OD已知,乘客换乘时间恒定且不低于平均值;③ 乘客对于单一层次轨道交通网络熟悉度恒定且已知;④ 乘客出行需求不因实际交通条件而改变。
2.2 模型构建
设θ为乘客对不同层次轨道交通网络及服务信息的熟悉度,为乘客对不同层次轨道交通间换乘点、线路覆盖区域及收车时刻差异的量化指标。乘客对网络及服务的熟悉度随θ增大而增大。出行路径涵盖多层次轨道交通网络的乘客常具有较低的熟悉度值。本文在文献[7]研究基础上,结合本文研究背景,增加了多层次轨道交通网络中各线路列车收车时刻差异值。本文构建的具体熟悉度计算公式为:
ωe=np+nc+hp+γewi,i∈[1,na]
(1)
式中:
ωe——乘客对各层次轨道交通网络的熟悉度;
γe——收车时刻差异影响系数;
na——网络中交通方式数量;
np、nc、hp——分别为单一层次轨道交通网络中换乘节点数量、不同层次轨道交通间换乘节点数量、单一层次轨道交通网络中的线路数量;
wi——多层次轨道交通网络中i交通方式列车收车时刻差异指标。
wi=(Dmax-Dmin)τi
(2)
式中:
τi——时刻差异校正系数;
Dmax、Dmin——分别表示线网中的最晚和最早收车时间。
多层次轨道交通网络OD间线路信息复杂度计算公式为:
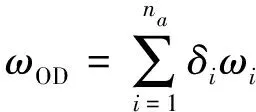
(3)
式中:
ωOD——OD间线路信息复杂度;
δi——乘客最短出行路径上交通方式Si的被选择线路是否存在已收车的情况,如已收车,取值为1,反之,取值为0。
文献中常将θ控制在[0.05,5.00]。本文在θ基础上根据影响因素进行调整,调整后的乘客对多层次轨道交通网络的熟悉度θd计算公式为:
θd=θ(1-f1ωOD)
(4)
式中:
f1——网络复杂度对熟悉度的影响因子。
以乘客出行时间为效用值,利用MML模型,构建乘客在出行条件限制下的路径选择概率模型:

(5)
其中:

(6)
式中:
Pr,OD——按OD间出行时间从小到大排列的第r条可行路径被乘客选择概率(不包含OD间的最短路径);
cr,OD——OD间第r条路径的效用值;
Lr,OD,i——交通方式Si该路径上的里程;
vi——交通方式Si的列车运行速度。
未选择其他可行路径的乘客成为滞留乘客,总滞留乘客qna计算公式式为:
式中:
tmax——多层次轨道交通网络中的最晚发车时间;
ξo,d,t——末班车时段乘客选择轨道交通的比例;
qOD,t——时刻tOD间客流量;
Pr,m,OD——OD间出行时间最短路径的选择概率;
Rr,OD,t,min——时刻tOD间第r条可行路径上列车定员数最小值。
模型目标1总滞留乘客最小数量Z1为:
因运营计划调整而造成的多层次轨道交通网络中各线路收车最小延时Z2计算公式即目标2为:

(8)
式中:
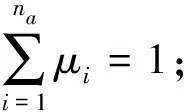
Di,j——交通方式Si的第j条线路的收车延时值。
模型的约束条件为:

(9)
式中:
xc,i,j,v、xc,m,i,j,v——第Si种制式轨道交通的第j条线路倒数第c次列车在车站v的到、发时刻;
v——各制式间换乘节点中的制式内换乘节点;
gi,j,v——第Si种制式轨道交通的第j条线路上车站v至v+1间运行时间;
hi.n——线路Si停站时间;
Tl,i——第Si种制式轨道交通的最晚发车时间;
hi.m——线路Si发车间隔时间;
Di,j、Di,j,max——分别表示第Si种制式轨道交通的第j条线路的收车延时值、延时值最大值。
3 多制式轨道交通末班车时刻表协同优化的算法设计
本文基于乘客出行需求及运营部门效益构建了多目标优化模型。对多目标优化模型进行处理时,常引入权重系数实现多目标向单目标的转化。但这种方式的主观性较大,结果形式较单一。本文提出嵌套Dijkstra搜索法的NSGA-II求解算法。Dijkstra算法用以求解末班车时段区域OD是否可达,基于NSGA-II算法搜索决策空间中的最优解集合,协调、组合后确定分目标最佳方案。
3.1 改进Dijkstra算法
本文以OD间乘客最晚乘车时间量化区域OD可达性,基于最晚到达时间问题(K-LAP),从乘客终点站最晚到达时间向前推,以确定最晚乘车时间,设定以下变量:
Xc,i,j,u,v——交通方式Si第j条线路倒数第c次列车在车站u的到达时间;
Xc,m,i,j,u,v——交通方式Si第j条线路倒数第c次列车在车站u的出发时间;
M(u,v,w)——从有向边e(u,v)至边e(v,w)的换乘时间;
tc,r,i,j,w,u,v——有向边e(w,u)至边e(u,v)的换乘冗余时间;
e(u,v)-——有向边的上一可行边;
E*——不同层次轨道交通的换乘节点与单一层次轨道交通换乘节点组成边的集合(利用标记法计算时仅考虑E*,其余边利用E*内涉及的关键节点进行推算)。
具体算法步骤如下:
步骤1:标记值初始化。针对每一终到点D,搜索其与不同层次轨道交通的换乘节点与单一层次轨道交通换乘节点组成边的集合,标记c(u,v)=X1,m,i,j,u,v,其余边标记为0。
步骤2:若E*内所有c(o,v)≥c(u,v),算法转至步骤6。o节点标记值即为起讫点OD间的最晚乘车时间,不满足则继续。
步骤3:记E*内c(u,v)最大的边为e(u*,v*),标记值记为c(u*,v*)。
步骤4:搜索e(u*,v*)的起点v*的所有邻接边e(w,u*),确定换乘可行的边,即满足tc,r,i,j,w,u,v≥0,记搜索的列车为c*,tc,r,i,j,w,u,v=c(u*,v*)-M(u,v,w)-Xc,i,j,u,v,基于初始出行路径客流qOD,以路径选择概率Pr,OD计算可行路径选择客流量。
步骤5:针对以u*为有向边的边e(u,v)更新其标记值c(u,v),判断e(u,v)倒数c*列车在u的发车时间Xc,m,i,j,u,v与c(u,v)的大小关系。若Xc,m,i,j,u,v>c(u,v),则c(u,v)=Xc,m,i,j,u,v、e(u*,v*)-=e(u*,v*),返回步骤2。
步骤6:算法停止。输出OD间乘客最晚乘车时间,c(o)=maxc(w,u),依顺序输出c(w,u),不可行的上一条可行边即为OD间最晚可达路径。
3.2 NSGA-II算法
NSGA-II算法为基于Pareto最优解架构建立的优化算法,一定程度避免了多目标优化算法中权重取值的主观性。本文将各OD间列车始发时刻作为算法基因,以染色体表征各方案,染色体数目为多层次轨道交通网络内线路数总和。在算法进化阶段,利用距离大小与各基因支配关系对个体进行筛分,最后基于融合变异随机法与单点交叉法的混合进化法处理个体,当目标函数值波动范围在阈值内时,算法停止。
4 实例分析
多层次轨道交通网络常包含高速铁路、城际铁路、市域铁路、城市轨道交通。本文以高速铁路与城市轨道交通的末班车时刻表协同优化为例进行实力验证,以合肥地铁、合福高铁、合武高铁、合蚌高铁、商杭高铁构成的多层次轨道交通网络为例分析模型算法的合理有效性。截止2022年5月,合肥地铁共开通5条线路,共有122座车站投入使用;线路内部共设8座换乘站,其中与高速铁路换乘的换乘站共有2座。基于多层次轨道交通网络特征构建城市轨道交通、高速铁路的双层复合拓扑网络,换乘信息如表1所示。

表1 合肥地铁各线与合肥各高铁线的换乘信息表
城市轨道交通与高速铁路的列车收车时间有差异,本文仅选取城市轨道交通末班车时段内的列车进行时刻表优化。现仅对2022年2月1日—28日的22:00—23:50时段内日平均客流量进行分析。表2为合肥地铁末班车OD日均客流量。表3为各高铁线路部分末班车日均客流量。部分模型参数取值见表4。

表2 合肥地铁2022年2月1日—28日部分末班车22:00—23:50时段内日均客流量

表3 合肥各高铁线路2022年2月1日—28日部分列车22:00—23:50时段内日均客流量
利用Matlab软件编程求解模型。NSGA-II 算法参数设置为:初始种群规模为150个,最大迭代次数为250次,最优前段个体系数为0.32。算法运行结束后共生成15个Pareto最优解。

表4 模型参数取值表Tab.4 Model parameter value
算法生成的Pareto front图及Pareto分析表分别如图4和表5所示。

图4 Pareto front图Fig.4 Diagram of Pareto front
由图4可见:末班车收车总延时值与区域OD不可达比例呈现近似反比的关系。当区域OD不可达比例为最小值0.149 6与最大值0.155 7时,末班车收车总延时值分别取得最大值12.715 min与最小值-10.272 min(负值表示优化方案末班车收车时间早于现行方案的)。
表5展示了部分Pareto解集合,其目标函数包含末班车收车最小延时值和不可达最小客流量2个子目标;方案序号从小到大表示末班车收车最小延时值目标的权重从小到大,不可达最小客流量目标的权重从大到小。序号1的方案具有最小的不可达比例,同时其具有最大的末班车收车延时值,可达比例较原方案增加了24.29 %。最优方案集合中,客流不可达比例随末班车延时值减少而提高,这是由于提前收车致使乘客的出行路径大量失效,产生大量不可行客流。第7个方案后,具有比现有开行方案更早的收车时间,在此条件下运营部门成本较低,同时具有比现行方案更低的不可达比例,因此运营部门可根据不可达比例与末班车收车延时值侧重于解集中选择合适的方案。

表5 部分Pareto最优解分析表Tab.5 Partial Pareto optimal solution analysis
5 结语
本文研究了多层次轨道交通网络末班车时刻表协同优化问题,并以合肥地铁、合福高铁、合武高铁、合蚌高铁、商杭高铁组成的多层次轨道交通网络为例进行了实例分析。结果表明:最优方案集均在一定程度优于现行方案,其中不可达比例最低的方案可达客流增加24.29%,发车时间推后56 s;不可达比例优于现行计划的方案中,末班车收车延时最小值为-10.272 min,城市轨道交通在10:50的不可达客流数量达到峰值,因此需增加相应时段的列车开行频率。实例分析表明模型具有有效性,为多层次轨道交通网络协调及决策提供了一定的理论支撑。
