基于Sobol序列抽样的斜拉索可靠度分析
2022-11-19张源翀王龙林
张源翀,王龙林
(1.广西北部湾投资集团有限公司,广西 南宁 530029;2.广西交科集团有限公司,广西 南宁 530007)
0 引言
大跨斜拉桥由于外观优美、经济性能优越以及跨越能力大等优点,而逐渐成为大跨桥梁的首选桥型[1-3]。其中斜拉索作为斜拉桥的重要受力构件,常发生如拉索腐蚀、锚头锈蚀、索力损失等问题,严重影响桥梁的安全性和可靠性[4-5]。因此,为保证斜拉桥的运营安全,对斜拉索进行可靠度评估具有重要的意义。
斜拉索可靠度研究方面,刘纲等[6]通过分析斜拉索的疲劳损伤,基于概率密度演化理论研究了斜拉索疲劳可靠度;谭冬梅等[7]考虑风荷载、车辆荷载以及覆冰荷载综合作用,对斜拉索进行了疲劳可靠度分析;刘发等[8]提出了腐蚀斜拉索承载力的退化模型,并研究了腐蚀程度和服役时间对斜拉索可靠度的影响;殷志祥等[9]基于Miner线性累积损伤理论评估了车辆荷载作用下斜拉索的疲劳可靠度水平;杜鹏刚等[10]通过响应面法研究了斜拉桥静力可靠度,分析表明,大跨斜拉桥主要失效路径是由于外侧斜拉索失效进而导致主梁悬臂跨中发生弯曲破坏。上述研究可以看出,斜拉索可靠度的研究已取得较大进展,众多可靠度分析方法虽能较为准确的进行斜拉索可靠度分析,但大部分计算方法计算复杂,不便于工程应用。欲将斜拉索可靠度分析应用于工程实际,需首先选取高效可行的可靠度分析方法。目前,Monte Carlo法是可靠度分析领域公认最为精确的分析方法,然而其计算成本昂贵,难以应用于实际工程可靠度评估[11]。近年来,选点策略方法得到不断发展,如重要性抽样法[12]、子集模拟法[13]、线性抽样法[14]以及Sobol序列抽样法[15]。其中,Sobol序列抽样法由于抽样效率高,而广泛应用于结构可靠度研究领域[16-18]。
鉴于此,本文基于Sobol序列和Monte Carlo法建立了斜拉索可靠度分析框架,以典型实际工程斜拉桥为研究对象,通过Sobol序列选取随机样本点,并结合有限元分析方法和Monte Carlo法计算了该桥的斜拉索可靠指标,以期为斜拉索可靠度分析提供参考。
1 基于Sobol序列的连续钢构桥可靠度分析方法
1.1 Sobol序列基本原理
Sobol序列是一种低差异序列,其分布均匀并且收敛较快,因此在各个领域得到了广泛的应用。假设ki为小于2i的正奇数,表达式为[19]:
(1)
式中,ki根据功能多项式产生,如式(2)所示。
f(x)=xr+c1xr-1+…+cr-1x+cr
(2)
当i>r时,ki和mi存在以下递归公式:
ki=c1ki-1⊕c2vi-2⊕…⊕crvi-r⊕vi-r/2r
(3)
mi=2c1mi-1⊕22c2mi-2⊕…⊕2rcrmi-r⊕mi-r
(4)
式中,⊕表示二进制中异或运算。
存在任意整数O,唯一表示与数基b=2的表达式:
(5)
式中,p表示大于等于lbO的最小整数;aj取值为0或1。
对此,Sobol序列第z个元素可计算如下:
Θz=a1v1⊕a2v2⊕…⊕apvp
(6)
限于文章篇幅,Sobol序列采样详细构造过程可参考文献。以某9维随机变量为例,采用Sobol序列抽取300个样本点如下页图1所示。由图1可以看出,Sobol序列采样结果较为均匀,可高效地选取随机样本点,进而应用于结构可靠度评估。
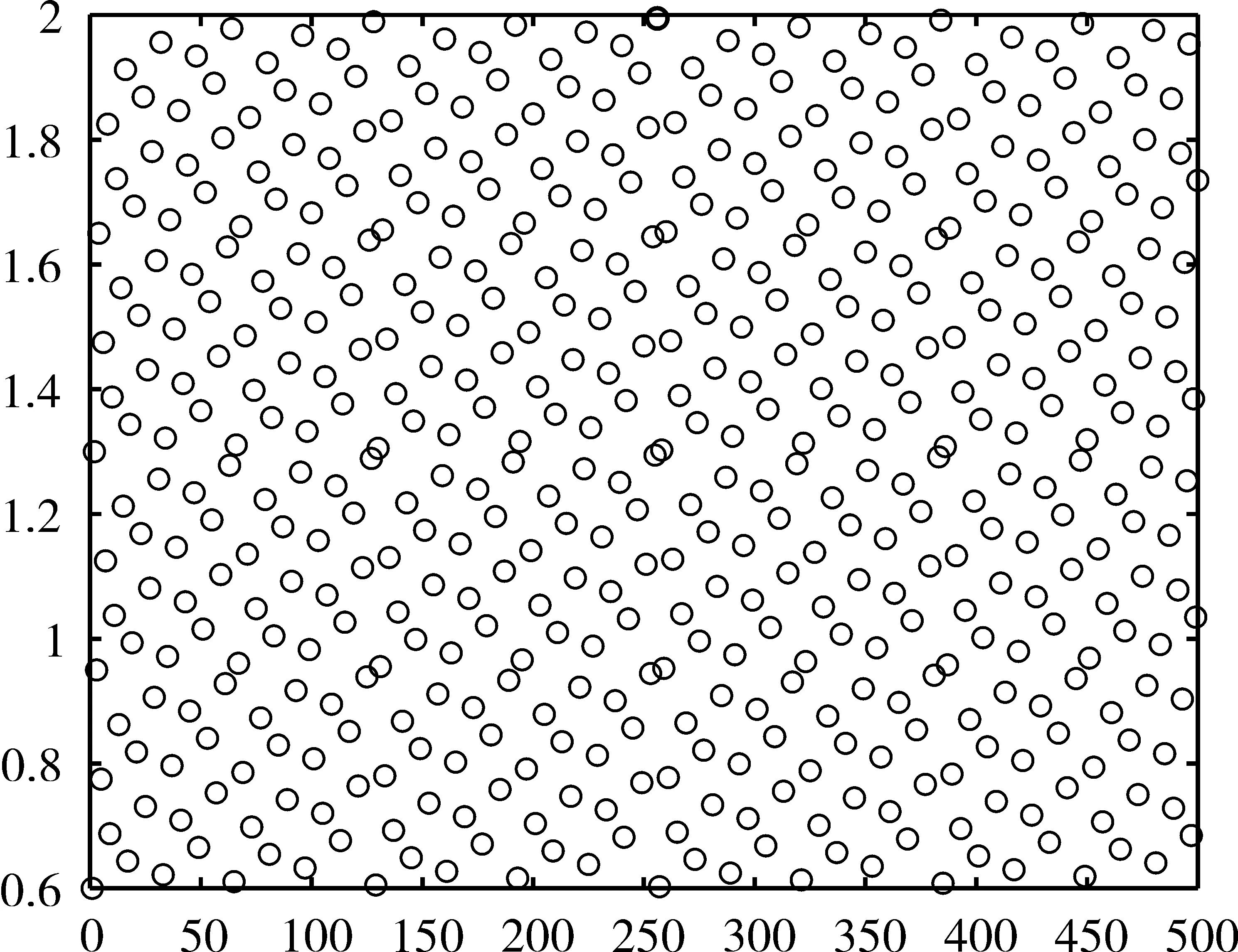
图1 Sobol序列采样结果示意图
1.2 失效概率及可靠指标计算
通过Sobol技术获取样本点后,可进一步结合Monte Carlo法计算结构的失效概率,计算公式如下:
(7)
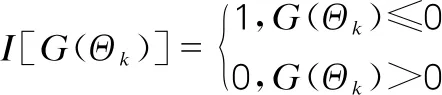
已知结构失效概率后,其可靠指标可相应计算得出:
β=-Φ-1(pf)
(8)
式中,Ф为标准正态分布函数。
2 基于Sobol序列的斜拉索可靠度分析流程及步骤
结合Sobol序列采样以及Monte Carlo法,可对斜拉索开展高效的可靠度分析工作,其具体流程如图2所示,详细步骤描述如下:
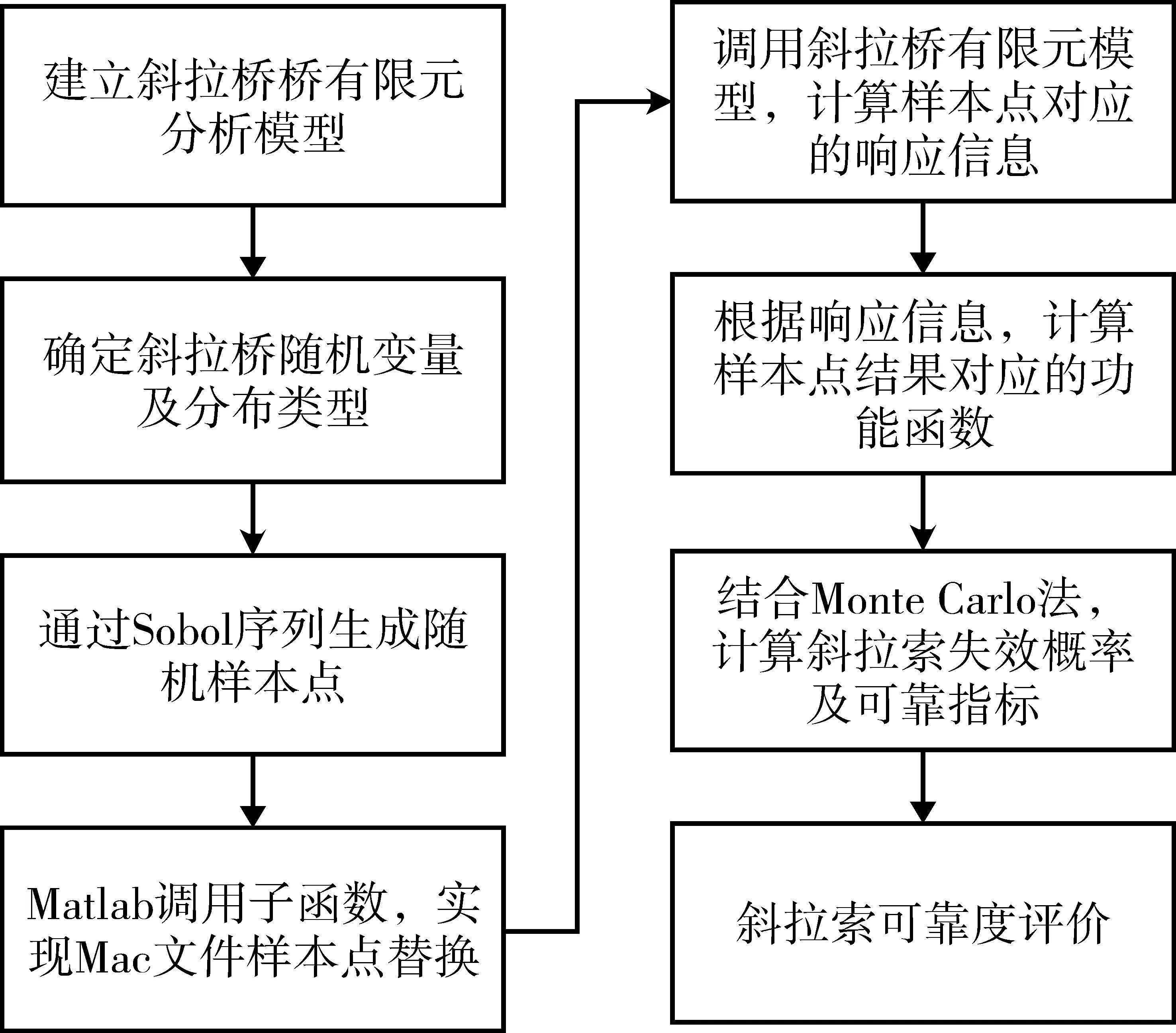
图2 基于Sobol序列的斜拉索可靠度分析步骤示意图
步骤1:基于通用有限元软件ANSYS,建立斜拉桥非线性有限元分析模型;
步骤2:参考现有研究,确定斜拉索常见随机变量并选取对应的分布类型;
步骤3:确定随机模拟次数N,基于Sobol序列在步骤2生成N个确定的随机变量样本点;
步骤4:编制Matlab程序,实现样本点批量写入有限元计算文件(Mac文件),最终形成N个有限元分析样本;
步骤5:基于N个有限元分析样本,通过Matlab调用ANSYS并将计算结果存储在指定文件夹;
步骤6:根据有限元分析结果,计算对应斜拉索的功能函数值;
步骤7:基于Monte Carlo法,统计总样本中失效次数,计算斜拉索失效概率和可靠指标;
步骤8:根据斜拉索失效概率和可靠指标,评价其安全性能。
3 基于Sobol序列抽样的斜拉索可靠度分析
3.1 斜拉索有限元模型
结合上述分析方法,对某典型工程开展斜拉索可靠度分析。该桥桥型为低塔斜拉桥,跨度布置为(110+220+110)m,斜拉索采用扇形布置,每个索面由10对斜拉索组成,其计算简图以及斜拉索编号如图3所示。
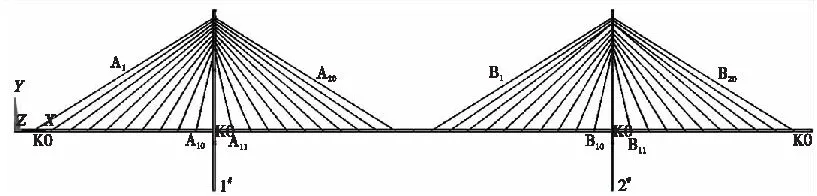
图3 斜拉桥斜拉索编号示意图
采用通用有限元软件ANSYS建立斜拉桥有限元分析模型,斜拉索采用LINK10单元模拟,桥塔、主梁和横向系梁采用BEAM4单元模拟。此外,桥塔底部以及两侧横梁支座进行节点约束,在桥塔横梁和支座处设置弹簧约束。考虑到斜拉桥具有较高的几何非线性,采用形状迭代法确定斜拉索初始索力,最终斜拉桥有限元模型如图4所示。
图4 斜拉桥有限元力学模型图
3.2 随机变量及功能函数
随机变量方面,本文主要考虑斜拉索弹性模量E1、容重γ1和主梁二期恒载q1三个随机参数,其具体分布类型、均值和标准差如表1所示。
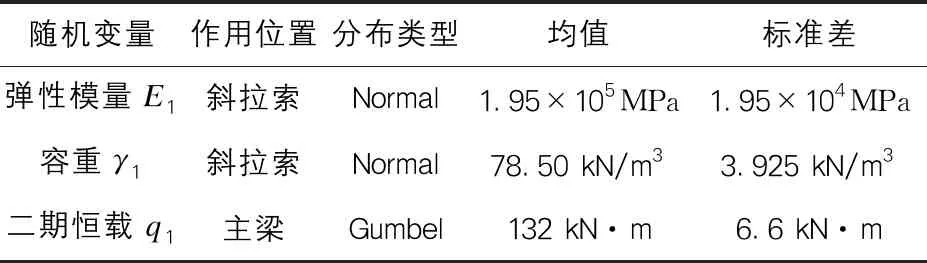
表1 斜拉桥随机变量及其分布类型数值表
对于斜拉索而言,其在运营过程中常发生强度破坏,进而影响斜拉桥整体承载性能。因此,本文可靠度分析主要考虑斜拉索的强度破坏,其功能函数可分别表示为:
(9)
3.3 可靠度分析
基于Sobol序列抽样方法,即可对本文斜拉索进行可靠度评估工作。首先,考虑到斜拉索失效破坏属于小概率事件,因此根据表1中随机变量参数及其分布类型,采用Sobol序列抽样方法抽取106个样本点;随后,调用斜拉桥有限元模型计算各个样本点对应的响应信息;最后,结合Monte Carlo法统计拉索失效次数,计算斜拉索失效概率pf和可靠指标β。此外,考虑到本文斜拉桥算例中斜拉索沿中跨跨中左右对称,因此本文仅计算了编号为A1~A10的斜拉索可靠度,其结果如表2所示。
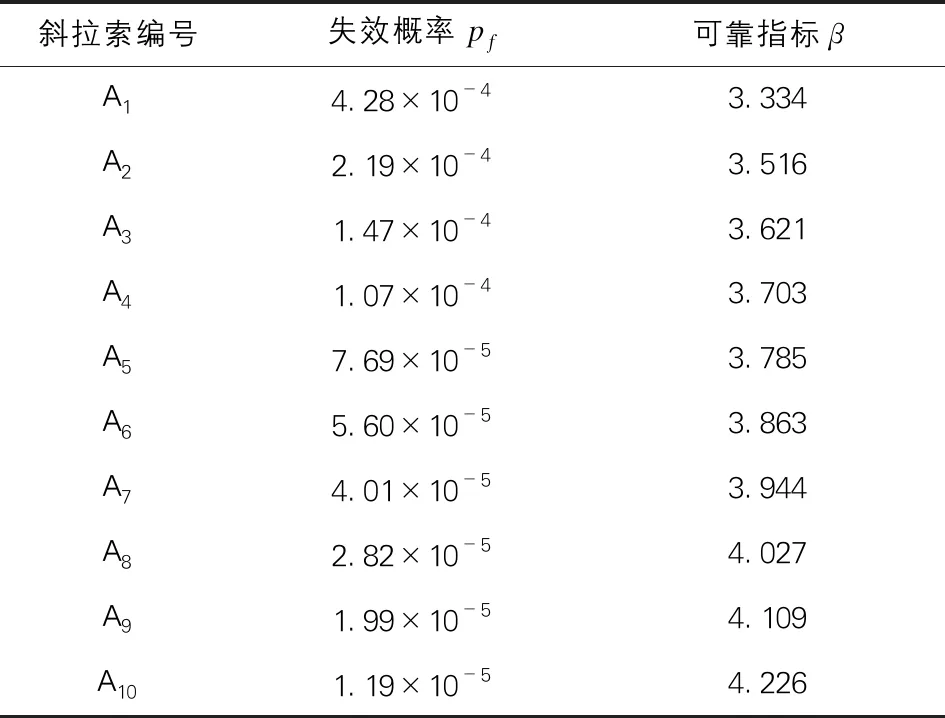
表2 斜拉索可靠度计算结果表
由表2可知,斜拉索失效概率主要集中在10-4~10-5,对应可靠指标分布在3.334~4.226以内,属于小概率失效事件。根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2012)[20]要求:桥梁结构一级结构承载能力极限状态下结构发生延性破坏的可靠指标β不应低于4.7。根据表2计算结果,本文算例的斜拉索可靠指标最大为4.226,低于规范中可靠度要求,建议对该桥采取相应的加固措施。
图5给出了斜拉索位置和可靠指标的对应关系,由图5可知,随着斜拉索编号的增加,即拉索长度的减小,斜拉索的可靠指标逐渐增大,即安全水平逐渐提高。而最外围拉索A1由于所承担的索力最大,因此可靠指标最小,拉索最易失效,应予以重视。
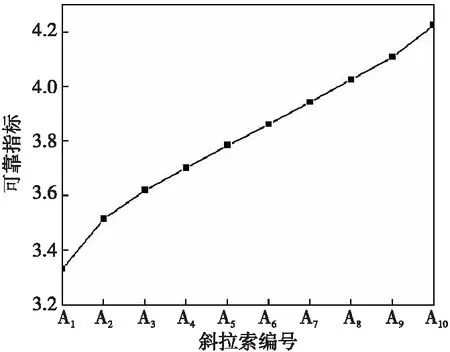
图5 斜拉索可靠指标曲线图
4 结语
斜拉索的可靠度水平对斜拉桥的运营安全具有重要的影响,本文以某大跨斜拉桥为例,基于Sobol序列抽样方法对斜拉索进行高效的随机抽样,并结合Monte Carlo法计算了斜拉索可靠度水平。分析结果表明:该算例中斜拉索可靠指标相较于规范要求偏低,建议对斜拉索采取一定的加固措施;随着拉索长度的增大,其承受的索力越大,可靠指标随着降低,应重视外围拉索的损伤状态;此外,基于Sobol序列抽样方法应用简单,能切实可行的应用于斜拉索可靠度分析,可为斜拉索概率评估提供参考。
