临近空间核爆炸碎片云运动特征与规律研究

刘 利 牛胜利 朱金辉 左应红 谢红刚

（西北核技术研究所 西安 710024）

碎片云是高空核爆炸［1］爆后裂变产物及产物膨胀吸收周围大气形成的粒子云。碎片云中包含大量具有放射性的裂变碎片［2-3］，裂变碎片持续向外释放强剩余辐射（γ辐射和β粒子），对空间飞行器和通信造成巨大的影响［1,4］。碎片云是研究剩余核辐射、电离层效应［5-6］、人工辐射带［7-9］、高空晚期核电磁脉冲［10］、极光与共轭区效应等高空核爆炸地球物理现象的基础。碎片云的强剩余辐射可能使得其内运动的卫星等飞行器功能失效甚至于直接毁伤［4］。碎片云运动激波引起的电离层扰动［11］和碎片云缓发辐射引起的大范围电离效应［12］可能导致短波通信路径转变、吸收增强，严重时会使得无线电通信直接中断，雷达搜索范围大大缩小。碎片云β粒子注入范艾伦辐射带，使得辐射带内电子浓度显著增强［7-8］，对穿越人工辐射带的轨道卫星造成损伤。所以碎片云运动规律研究具有重要物理意义。

模拟碎片云运动状态的主要手段包括流体力学模拟方法、磁流体力学模拟方法和混合粒子模拟方法。Stuart等［13］采用流体力学方法计算了高空小型化爆碎片云半径随时间演变；Sergeev［14］同样采用流体力学模型模拟碎片云运动，并根据碎片云扩张速度计算了碎片云引起的电离层扰动；Zinn等［15］采用磁流体力学方法计算了等离子体球在地磁场作用下的扩张过程；Brecht等［16］采用粒子模拟和磁流体模拟混合模型模拟了碎片云内粒子分布演化过程；彭国良等［17］提出了基于流体-磁流体-粒子混合方法的高空核爆炸碎片云模拟方法；乔登江等［18］采用流体力学方法模拟了百万吨当量百公里高度核爆条件下的碎片云运动；杨斌等［19-20］采用磁流体力学方法研究了高空核爆炸碎片云早期扩展情况；刘利等［21］在流体力学方法的基础上引入了X射线加热大气模型，实现了碎片云扩展模型、上升模型和X射线沉积模型的耦合，能够给出长达几分钟的核爆炸碎片云运动参数。

随着临近空间（30～80 km高度范围内）的军事与商业价值日益增强［22］，临近空间核辐射环境研究也愈发重要。相比于80 km以上的高空核爆炸，临近空间核爆炸碎片云向外扩张速度较慢，覆盖范围较小，但由于碎片云内部裂变产物浓度高，释放的γ射线和β粒子强度大，其对影响范围内的空间飞行器和通信的作用更强。虽然国内外学者已建立了多种碎片云运动数值模拟方法，但临近空间核爆炸碎片云运动规律的定量研究还少有报道。因此本文利用建立的临近空间碎片云流体力学计算模型，对当量1 kt～10 Mt、爆高30～80 km核爆炸碎片云运动进行了系统性计算研究，得到了碎片云运动典型特征参数，并总结了临近空间核爆炸碎片云运动的典型特征规律。

1 物理模型和计算方法

在临近空间高度范围内，碎片云受到的热压力远大于磁压力［21］，因此可以忽略磁场的影响，采用流体力学模型来研究碎片云运动规律。受核爆炸剩余能量的驱动，碎片云迅速膨胀向外扩展。另一方面，高层大气在X射线加热作用下急剧升温，碎片云云体上下受到压力梯度的影响而整体上升。所以碎片云的运动可以分为扩展运动和上升运动两个方面来计算。

1.1 碎片云扩展模型

核爆炸碎片云受爆炸能量驱动不断膨胀向外扩展，并吸收稀薄大气使之成为云体的一部分，如图1所示。假设大气密度均匀，则碎片云呈球形扩展。假定球体内某点速度v随半径r为最简单的线性分布，即：

图1 碎片云扩展示意图Fig.1 Diagram of debris expansion

式中：r为球内某点球心距；R为球体半径。

则考虑卷入周围大气的动量守恒方程为［21］：

将式（2）两侧乘以r并对体积积分可得到［21］：

式中：α为碎片云质量分布系数；Q为爆炸总能量；η为碎片云得到的总能量份额；γ为大气绝热指数。将式（3）转化为一阶低阶方程组，采用四阶龙格库塔R-K法求解可以得到碎片云半径与时间的关系。

1.2 碎片云上升模型

碎片云的上升过程中整体在竖直方向上受到云体上下表面的压强差和自身重力的综合作用，其运动方程可写成：

式中：Z为上升高度；p为大气压强；θ为碎片云面元dσ的外法线与垂直向上方向的夹角。

其中：大气的压强：

式中：N是空气粒子数密度；k是波尔兹曼常数；T是周围空气温度。T=Tb+ΔT，其中：Tb是背景大气温度；ΔT是X射线能量沉积在大气中的增温。T主要由X射线在大气中的能量沉积造成的增温及其相应的辐射冷却来决定。

利用式（4）计算出垂直方向上的加速度，进而得到垂直方向上的速度。由于碎片云不断卷入大气，还应考虑碎片云与卷入大气的垂直动量守恒来修正垂直速度，即：

式中：m0、v0为修正前的碎片云质量与垂直方向速度；m1为此时间步长内卷入大气质量；v1为修正后碎片云垂直方向速度。

1.3 X射线加热大气模型

X射线加热大气过程与X射线在大气中的能量沉积相关，可以采用平均自由程来计算。X射线在大气中的平均自由程λ［1］为：

式中：TX为黑体谱温度，keV；ρ0为海平面大气密度；ρ为高空大气密度。

X射线在大气中输运R距离后，半径为R的球体内空气的内能增加等于空气吸收的能量，即：

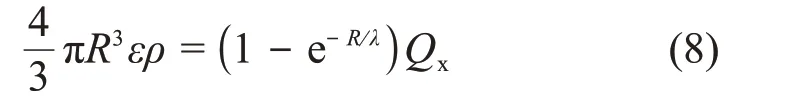
式中：ε为气体内能，与大气温度和ρ/ρ0密切相关；Qx为X射线总能量。联合式（8）和稀薄空气高温状态方程可求解得到X射线致大气温升。

X射线加热大气后，高温大气向外辐射发光并冷却。根据辐射迁移理论来计算，对于球形辐射体，单位时间单位体积内辐射出去的能量［1］为：

式中：λp为平均自由程。通过大气的状态和λp算出可以大气温度随时间的下降。

根据式（8）和式（9）计算得到X射线加热大气致大气温升分布，利用碎片云扩展模型计算下一时刻的碎片云径向分布，在利用碎片云上升模型计算下一时刻碎片云的上升高度，将三个模型耦合循环迭代，就可以实现碎片云整体运动情况的数值模拟。

1.4 模型验证

为了验证计算模型，计算了爆高77 km、当量3.8 Mt、爆炸位置在约翰逊顿岛上空的美国TEAK核试验碎片云的演化过程。文献［18］取弹体质量M0=103kg，弹体半径R0=1 m，初始上升速度v0=1.2 km·s-1（即导弹上升的末速度），碎片云的能量占总爆炸能量的份额η=20%，取α=1，γ=1.4，ξ=1开展计算。计算表明，碎片云初始状态即弹体参数对于碎片云长时间运动状态影响较小。模拟得到了碎片云运动高度、水平半径、扩展速度、上升速度和质量等参数随时间的演化关系。图2给出了不同时刻的碎片云中心高度与最大水平半径模拟结果与实验测量数据［18,23］的对比。碎片云具有明显的上升与下降过程，上升时间约为4 min，然后开始下降，下降过程趋于平缓。模拟结果与测量数据基本吻合，变化规律一致。模拟得到的碎片云由最开始的球形逐渐演化为类似于圆柱的倒梨形，也与文献［23］中的演化一致。

图2 TEAK试验碎片云的最大水平半径(a)和中心高度(b)与测量数据的对比Fig.2 The comparison between the measurements and the simulated maximum horizontal radius(a)and center height(b)of debris in TEAK

2 碎片云运动特征与规律

2.1 系统性计算分析

取当量1 kt、5 kt、10 kt、50 kt、100 kt、500 kt、1 Mt、3.8 Mt、5 Mt、10 Mt，高 度30 km、40 km、50 km、60 km、70 km、80 km等初始条件计算碎片云参数变化。弹体质量等相关初始参数与上文中TEAK试验一致。模拟得到了不同爆高不同当量下核爆炸碎片云水平半径、中心高度、上升速度、扩展速度和质量等参数随时间的演化。

图3给出了爆高30 km、50 km和80 km不同当量核爆炸碎片云的中心高度、水平半径和纵横比随时间的变化。图4给出了爆高80 km当量10 Mt核爆炸碎片云上升速度和总质量随时间变化。爆后受爆炸能量驱动碎片云急剧扩展，不断卷入周围大气。由图4可以看出，碎片云水平半径随爆高和当量而增加。爆后2 s内碎片云水平半径迅速增加，随着卷入大气碎片云总动能减少，碎片云水平半径随时间增加变为缓慢，类似于线性。碎片云扩张初始阶段，卷入大气质量远小于弹体质量，根据式（3）可以得到，扩展半径R与时间t的关系可简化为dR/dt=(2ηQ/αM0)1/2。碎片云扩张中后期，卷入大气远大于弹体质量，根据式（3）可以得到，扩展半径R与时间t的关系可简化为dR/dt=[(γ-1)ηQ/ξαM]1/2。卷入大气后碎片云总质量越多，碎片云扩展速度越慢。由于大气密度随高度指数衰减，碎片云上升后卷入大气密度远小于在爆心处卷入大气密度，所以碎片云总质量一般在爆后10～20 s内达到最大（图4）。当碎片云总质量达到最大后，dR/dt基本不变，碎片云扩张中后期水平半径随时间基本呈线性变化。

图4 碎片云上升速度和总质量随时间变化Fig.4 The ascending velocity and total mass of the debris change over time

爆后1 s以内碎片云扩张不断卷入周围大量静止空气，根据动量守恒，碎片云上升速度由火箭末速度1.2 km·s-1迅速降低至约0。而后由于X射线沉积造成碎片云云体上下方空气温升不一致，碎片云受上下方压力驱动碎片云快速上升。碎片云上升速度一般在10～20 s之间达到峰值（图3）。爆高越高当量越大，碎片云上升速度峰值越大。爆高30 km当量1 kt核爆炸碎片云上升速度峰值仅为0.2 km·s-1，爆高80 km当量10 Mt核爆炸碎片云上升速度最大可达2.3 km·s-1。随后上升速度逐渐降低，碎片云上升逐渐变慢。计算结果表明：当量越大，X射线沉积越多，碎片云上升速度越大；爆高越高，碎片云卷入空气质量越小，碎片云上升速度越大。碎片云上升高度同样随当量和爆高增加。

核爆炸碎片云初始为球形，扩张为球形扩张。随着碎片云的扩张和上升，其形状随之而改变。图3还给出碎片云纵横比随时间的变化。纵横比即碎片云垂直方向直径与水平方向直径之比。当纵横比等于1时，碎片云保持球形。当纵横比大于1时，碎片云演化类似于倒梨形。当纵横比小于1时，碎片云类似于扁椭球形。图5给出了模拟的爆高30 km当量1 kt和爆高80 km当量10 Mt核爆炸不同时刻的碎片云形状。当当量较小爆高较低时，碎片云纵横比小于1，即碎片云演化趋向于扁椭球形。爆高30 km当量1 kt核爆炸碎片云形状由圆形演化为类似于一个上下受到压迫的扁椭球，如图5所示。当当量较大爆高较高时，碎片云纵横比大于1，即碎片云演化趋向于圆饼形。爆高80 km当量10 Mt核爆炸碎片云形状由圆形演化为典型的倒梨形，如图5所示。碎片云演化为扁球形和倒梨形的特征规律与文献描述［1］一致。计算结果表明，爆高70 km当量5 Mt的核爆炸碎片云纵横比保持在1附近，即碎片云基本保持球形。爆高小于70 km当量小于5 Mt的核爆炸碎片云形状都由球形演化为扁椭球形，即临近空间兆吨级以下的核爆炸碎片云形状基本都为扁椭球形。

图3 不同爆高、不同当量核爆炸碎片云参数随时间变化(a)中心高度，(b)最大水平半径，(c)纵横比Fig.3 The parameters of debris change over time with different explosive heights and different equivalents(a)Center height,(b)Maximum horizontal radius,(c)Aspect ratio

图5 模拟的不同时刻的碎片云形状Fig.5 The simulated shape of debris at different time

为了定量分析临近空间核爆炸碎片云运动规律，计算给出了不同爆高、不同当量核爆炸碎片云的最大上升高度和爆后5 min最大水平半径如图6所示。碎片云最大上升高度决定了碎片云最终高度，与电离层效应和人工辐射带辐射强度密切相关。最大碎片云水平半径与电离层效应和人工辐射带辐射影响范围密切相关。

图6 模拟的碎片云的最大上升高度(a)和5 min最大水平半径(b)Fig.6 The simulated maximum ascending height(a)and horizontal radius(b)at 5 min of debris

碎片云最大上升高度随当量和爆高增加。千吨级临近空间核爆炸碎片云最大上升高度仅为13～50 km，兆吨级临近空间核爆炸碎片云最大上升高度可达20～400 km。爆高30 km的核爆炸碎片云最大上升高度为13～43 km，爆高80 km的核爆炸碎片云最大上升高度为30～390 km。碎片云水平半径随当量和爆高增加。千吨级临近空间核爆炸5 min后碎片云最大水平半径为4～40 km，兆吨级临近空间核爆炸碎片云5 min后最大水平半径可达14～200 km。爆高30 km核爆炸碎片云5 min后最大水平半径为4～28 km，爆高80 km核爆炸碎片云5 min后最大水平半径为22～214 km。

2.2 与文献估算方法对比

文献［24］给出了一套基于图表和经验公式的估算碎片云主要参数的方法。该方法仅适用于当量10 kt～10 Mt之间。图7给出了采用估算方法计算的临近空间核爆炸碎片云的最大上升高度和爆后5 min碎片云的最大水平半径。

图7 估算方法计算的碎片云的最大上升高度(a)和5 min最大水平半径(b)Fig.7 Computed maximum ascending height(a)and horizontal radius(b)at 5 min of debris by estimating method

对比图6和图7可以发现，计算模型和估算方法计算得到的不同当量、不同爆高的碎片云最大上升高度与水平半径在数值上整体较为接近，变化规律基本吻合。碎片云最大上升高度随当量和爆高增加。碎片云最大水平半径随当量和爆高而增加，在兆吨级以上大当量高爆高情况下，两者略有差异，模型计算的碎片云最大上升高度与水平半径相对较小。估算方法和计算模型计算的爆高77 km当量3.8 Mt的TEAK试验爆后310 s碎片云的最大水平半径分别为202 km和360 km，本文模型计算结果与测量数据更为接近。估算方法相差较大的可能原因为估算方法采用的曲线或者公式对碎片云参数变化的描述较为简单，基本上为线性变化，致使其计算结果与部分试验数据存在一定差异。估算方法给出的碎片云形状在爆高较小当量较小时由球形演变为圆饼形，在爆高较大当量较大时可能演变为圆柱形，与计算模型给出的更贴近实际形状的扁椭球形和倒梨形一致。

综上所述，数值计算模型计算结果规律与文献估算方法相似，在高爆高大当量情况下计算模型结果与实验更加接近。估算方法与模型的最大区别在于：估算方法基于试验现象与数据得到的唯象经验计算方法，计算得到碎片云半径、高度和厚度等主要参数；数值计算模型基于理论计算公式的推导与数值求解，求解得到碎片云分布的时空演化过程，进而得到碎片云质量、加速度、半径、高度、厚度和形状等参数。由于估算方法基于图表和经验公式，其计算瞬间就能完成，而数值计算模型的计算时间一般为分钟量级。文献中估算方法仅适用于10 kt～10 Mt的当量区间。本文计算模型适用范围更广，可以给出当量10 kt以下低威力核爆炸碎片云运动参数，能够为低威力核爆炸地球物理现象研究提供理论数据。

3 结语

为研究不同当量不同爆高核爆炸碎片云运动规律，本文根据建立的临近空间核爆炸碎片云运动流体力学计算模型，对当量1 kt～10 Mt爆高30～80 km范围的核爆炸碎片云参数展开了系统性模拟计算，得到了不同当量不同爆高核爆炸碎片云水平半径、中心高度、扩展速度、上升速度和质量等参数随时间的演化，总结了碎片云典型特征参数随当量和爆高的变化规律。研究得到的碎片云上升高度、水平半径、上升时间和形状等的变化规律与文献估算方法给出的变化规律基本吻合。

得到以下主要规律性认识：1）临近空间核爆炸碎片云水平半径爆后2 s内迅速增加，而后增加速率逐渐变缓，扩张中后期碎片云半水平径随时间基本呈线性变化；2）碎片云水平半径随当量和爆高增加；3）碎片云上升速度随当量和爆高增加，碎片云上升速度一般在10～20 s之间达到峰值；4）碎片云最大上升高度随当量和爆高增加；5）碎片云初始为球形扩张，当量较小爆高较低（爆高小于70 km，当量小于5 Mt）时，碎片云演化为扁椭球形；当量较大爆高较高时，碎片云演化为倒梨形；6）临近空间千吨级核爆炸碎片云最大上升高度为13～50 km，爆后5 min最大水平半径为4～40 km；临近空间兆吨级核爆炸碎片云最大上升高度为20～400 km，爆后5 min最大水平半径为14～200 km；爆高30 km核爆炸碎片云最大上升高度为13～43 km，爆后5 min最大水平半径为4～28 km；爆高80 km核爆炸碎片云最大上升高度为30～390 km，爆后5 min最大水平半径为22～214 km。

研究成果可为剩余核辐射、电离层效应、人工辐射带、极光与共轭区效应等地球物理现象提供准确有效的缓发辐射源。

作者贡献声明刘利：计算模型开发，程序设计，程序验证，数据分析，文章撰写；牛胜利：参与计算模型开发，程序设计，指导总结数据特征规律，文章修改；朱金辉：提供技术指导，审阅文章；左应红：参与数据分析，审阅文章；谢红刚：参与计算模型开发。