基于多维特征分析的低压用户相别识别研究
2022-11-18杨菊芳
杨菊芳,王 伟
(1.国网南昌市青山湖区供电公司,江西 南昌 330006;2.国网九江市桑柴区供电公司,江西 九江 332100)
0 引言
降低线损是电网企业降低碳排放的重要途径,准确识别用户相别对线损管理至关重要。随着高速电力线载波(High Speed Power Line Carrier,HPLC)在配网的高比例推广应用,基于HPLC高频采集的用户相别识别愈发被重视。HPLC具备相位识别能力,但准确性待核实验证。针对这问题,如何发挥HPLC优势,确保台区用户相别数据准确,是国内外学者研究的重点之一。
国内外学者对该主题做了相关研究。文献[1]提出基于HPLC通信模块可实现台区拓扑信息、台区相位识别。不足是计算方法不清晰。文献[2]基于电压曲线相似度的电力相位识别技术,采用小波分析技术抑制电压的噪声信号,利用向量夹角余弦法来识别曲线相似度的电力相位。不足是对电压波形幅值权重系数的选择缺乏必要的论证。文献[3]提出通过电压数据相关性算法、灰色关联分析算法获得单相电能表的安装相别。不足是对样本量有要求,样本量少不准确,而且缺乏假设检验。文献[4]提出了一种新的数据驱动相位辨识算法,采用非线性降维算法从电压时间矩阵中提取特征,采用基于密度的带噪声的应用程序空间聚类(DBSCAN)算法将客户划分成任意形状的簇。在IEEE欧洲低压测试Feeder对算法进行了测试准确度90%以上。不足是计算复杂,准确度需进一步提升。文献[5]通过电压相似性判断和基于Hausdorff距离算法进行相位识别,准确率为78%。不足是准确度需进一步提升,而且Hausdorff距离对两条曲线整体位置敏感,曲线间的最短距离不敏感[6],对异常点不敏感[7]。电压曲线存在奇异点,此方法有一定局限性。
以上研究共性问题在于主要对电压曲线进行相似度分析、相关性分析,准确率不太高,同时缺乏必要的业务逻辑验证和假设检验分析。因此,文中结合技术及业务逻辑,计算电压、电量曲线的余弦相似度、皮尔逊相关系数,分析台区用户相别,采用K-S假设检验评估其准确性,使得用户相别识别具备技术及业务分析的有效性。
1 用户相别多维度识别分析
基于3个维度的分析指标,2个维度的数据样本,构建含6个维度特征的用户相别分析模型。
1.1 余弦相似度
余弦相似度是通过计算两个向量的夹角余弦值来评估两者相似的程度。对向量幅值不敏感,对向量方向敏感。当两个向量有相同的指向时,余弦相似度的值为1;两个向量夹角为90°时,余弦相似度的值为0;两个向量指向完全相反的方向时,余弦相似度的值为-1。余弦相似度计算公式为式(1)。
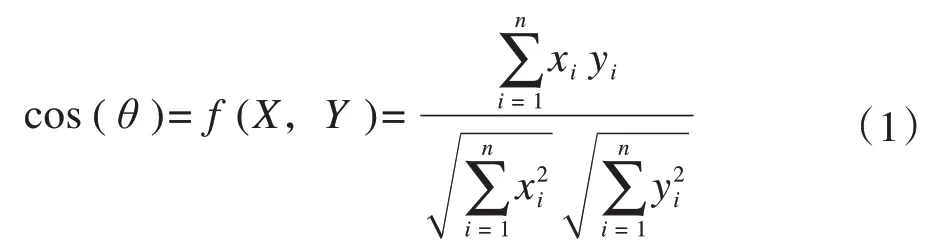
1.2 皮尔逊相关系数
皮尔逊相关系数广泛用于衡量两个变量之间的相关程度,其值介于-1与1之间。绝对值越大,说明相关性越高,正值表示正相关,负值表示负相关。皮尔逊相关系数可分别计算电压曲线、电量曲线相关性,具体见式(2)。
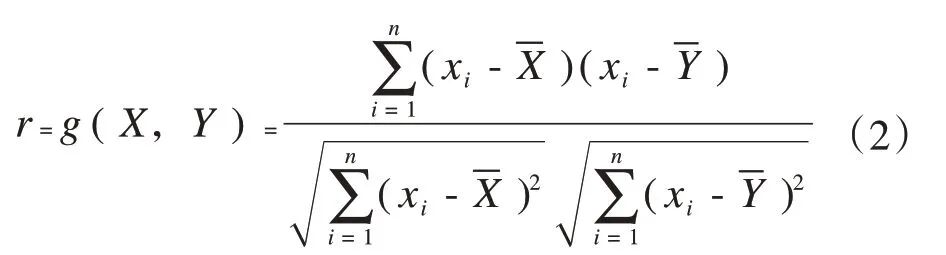
式中,r为皮尔逊相关系数,无量纲分别为向量X、Y的均值。
1.3 K-S检验
由于某时间段内的电压、电量曲线分布特性及统计参数均未知,判断其差异宜采用非参数检验。K-S检验(Kolmogorov-Smirnov test)是一种比较两组数据分布是否存在显著差异的非参数检验,且对样本分布形状差异灵敏[8-9]。文中利用K-S检验判断两条电压、电量曲线是否存在显著差异,验证台区用户相别准确性。K-S检验方法如下:
对样本F1(x)、F2(x),假设
这里的秦光仪是向孔尚任介绍弘光遗事之人,在《桃花扇》的创作过程中起到了至关重要的作用,但由于文献阙如,他与孔尚任的关系不得而知。那么“舅翁”是什么意思呢?一般有以下三种说法。
H0:F1(x)、F2(x)分布无显著差异;
H1:F1(x)、F2(x)分布有显著差异。
假设D为样本F1(x)、F2(x)差距最大值:
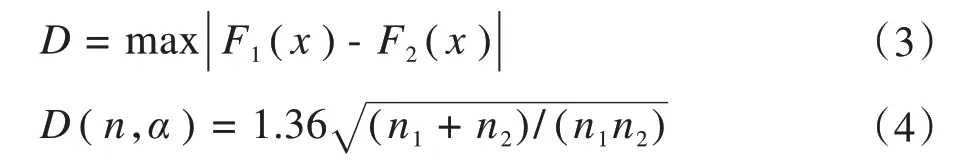
式中,D(n,α)是显著水平为α且样本容量为n时的拒绝临界值。文中取α=0.05,n=n1=n2=15。当D<D(n,α),p>α则接受H0,否则接受H1。
1.4 多维度特征分析
分别从电压、电量曲线进行余弦相似度、皮尔逊相关系数及K-S检验计算。
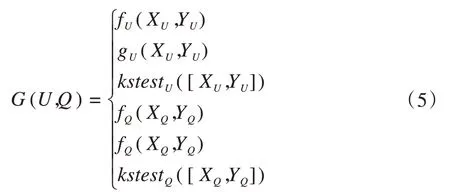
式中,U为电压样本;Q为电量样本;f为余弦相似度函数,同式(1);g为皮尔逊相关系数,同式(2);为K-S检验函数,方法为1.3章节。按照式(5)计算得到6组特征数据,分析台区用户相别,如图1所示。
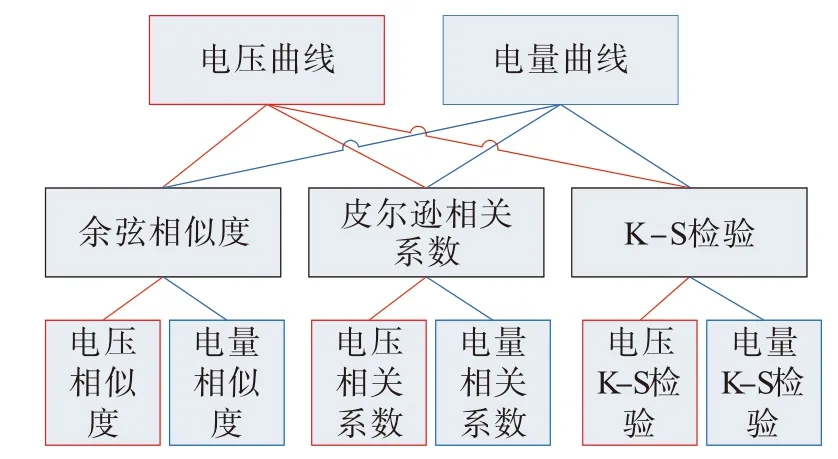
图1 多维特征分析
2 台区相位识别流程
首先采集台区关口及用户的电压、电量曲线数据,构建计算样本矩阵,根据式(1)至式(4)开展皮尔逊相关系数、余弦相似度计算,并进行K-S假设检验,流程如图2所示。
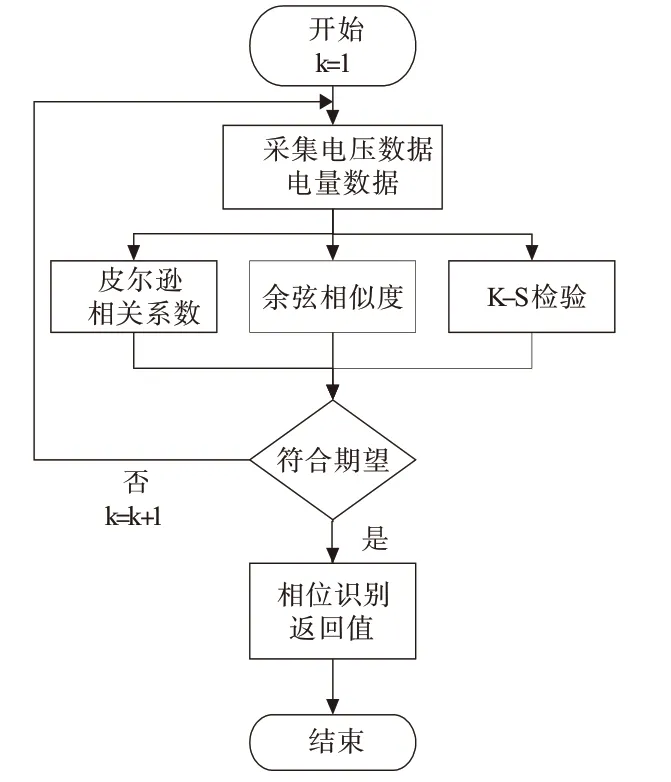
图2 流程图
皮尔逊相关系数对方向不敏感,作为相位识别初步参考;余弦相似度对方向敏感,作为相位识别重要依据。期望:当电压曲线、电量曲线余弦相似度0.9以上,且K-S假设检验接受,则认为相位识别准确和有效。
3 算例
3.1 电压曲线
文中采用台区某日经过脱敏的电压数据,关口电压曲线如图3所示,86个用户电压曲线如图4所示。

图3 台区关口电压

图4 用户电压
图3中,关口电压曲线分布随机,无明显规律可循;图4中,86个用户电压曲线呈现典型的聚集特征,轮廓与图1关口电压曲线具有趋同性。图2部分电压数据波动大,距离中心轮廓较远。采用k-means聚类对用户电压曲线数据进行分类,如图5所示。
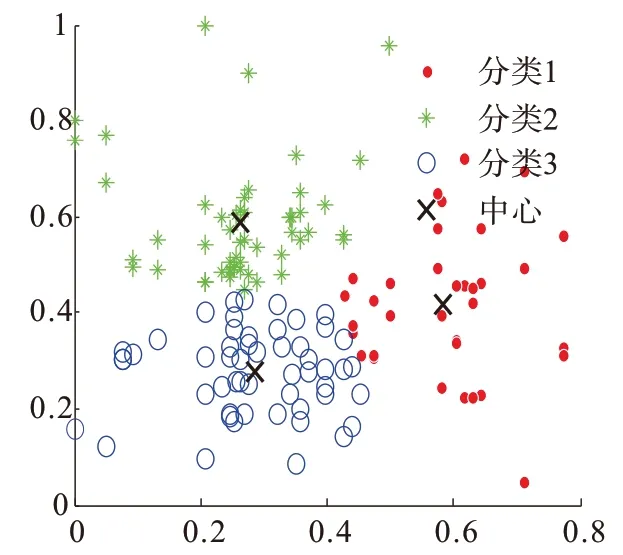
图5 用户电压数据聚类
图5中,坐标轴均为电压。发现存在部分电压数据距离中心位置较远,即奇异值,与图4相适应。
3.2 电量曲线
台区关口及用户电量曲线如图6、图7所示。
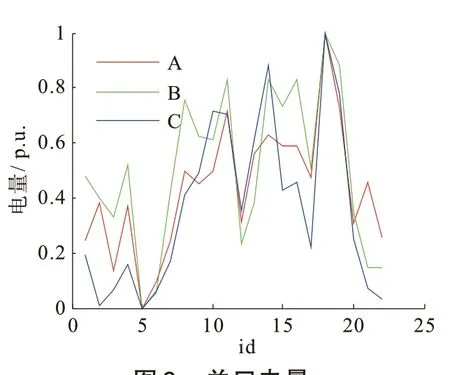
图6 关口电量
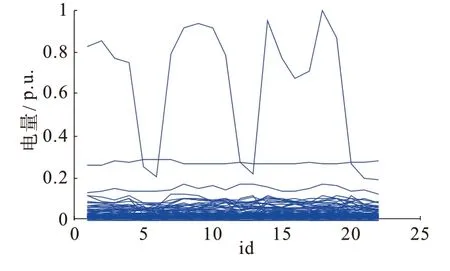
图7 用户电量
图6、7中,关口各相电量在部分时间段呈现趋同性,偏差小;大部分用户电量曲线波动小,个别用户电量曲线波动大,少数用户电量曲线平直或为0。
图8中,用户电量聚类发现多数用户电量分布集中,距离中心位置近。少数用户距离中心位置较远,与图7曲线分布特性吻合。

图8 用户电量聚类
3.3 台区相位识别
根据式(1)-(5),在Matlab环境编程,对以上电压、电量样本数据进行余弦相似度、皮尔逊相关系数计算,开展K-S检验,如表1所示。

表1 相位识别结果
表1中,A相准确率偏低。总的准确率均值为90.56%,符合期望。工程实际中,由于用户电能表存在时钟不同步、0电量、恒定电量、电量小微波动等因素的干扰,表现为用户电压曲线平移、电量曲线平直或曲线波动不明显。皮尔逊相关系数、余弦相似度对此状态无法准确识别。
4 结语
文中结合技术及业务逻辑,计算电压曲线及电量曲线的余弦相似度、皮尔逊相关系数,并采用K-S假设检验,分析台区用户相别,准确率符合预期,得出以下结论。
1)对电压、电量曲线进行皮尔逊相关性、余弦相似度分析及K-S检验,可提高相别识别的准确度,在工程实际中有借鉴意义。
2)在时钟不同步导致电压曲线平移,以及在电量曲线平直的状态下,对相关系数、余弦相似度的计算造成明显干扰,导致结论错误。在以后研究中进一步拓延伸。
