基于粒子群算法的储能优化配置技术应用研究

严飞飞，张 扬，曹正东，李 扬，甘智豪，邹 量

（1.国网江西省电力有限公司南昌供电分公司，江西 南昌 30031；2.国网江西省电力有限公司信息通信分公司，江西 南昌 330031；3.南昌大学信息工程学院，江西 南昌 330006）

0 引言

由于传统化石能源例如石油、煤炭等被过度开发利用以及生态环境的持续恶劣，导致了能源危机日益严重，为此我国也提出了“碳达峰”“碳中和”这一推进绿色发展的庄严承诺。为了解决能源需求越来越大这个问题，可再生能源大有替换传统化石能源的趋势，这是由其更加丰富的储量和更加可观的环保效益所决定的。然而，光伏发电、风力发电等一些新能源集成发电新方式对现有电力系统运行来说，其分布式发电过程伴随着电功率传递不稳定、不连续发电的诸多特点，这自然就导致了可再生能源并网会给配电网带来电压波动等问题[1]，同时，这也使县域电网面临合理规划、安全稳定运行的多重挑战，县域电网储能优化配置技术的应用则是解决上述问题的有力措施，并且，合理配置储能还可以利用峰谷套利降低用电成本。

文献[2]从分布式光伏和蓄电两个方面出发，以电网损失和电网的电压偏移作为最优的研究对象，对各种功率等级及负载形式下的最优选择进行了研究，并利用微粒群方法对目标进行了求解；文献[3]从经济性角度出发，构建了一套基于经济性和电压稳定性两个最优目标的二级模型，并对一次投资成本、网络损耗成本、主网购成本和电网电压偏离进行了研究；文献[4]提出了以储能功率和容量配置的投资成本为外层目标，以系统联络线功率波动最低为内层目标的双层模型，对储能进行优化配置；文献[5]以平抑电网联络线功率波动为主要目标进行综合能源站储能装置容量配置；文献[6]考虑到分布式电源的建设运行成本及网络损耗，提出了一种改进萤火虫算法和天牛须算法的混合算法，并建立数学模型，通过IEEE33节点仿真验证模型的合理性及方法的正确性。根据以上文献可以得出，对于储能的配置优化有许多可选的指标，并且对于接入电网的分布式储能配置优化是很有必要的。在寻优算法的选取上，粒子群寻优算法在电力系统的储能配置优化中具有重要作用，此方法基本原理简单，收敛速度快，寻优精确度的也较高，便于工程实际实现，可以比较全面的求解分布式储能经济最优解。

1 储能配置模型

文中建立了以储能建设运维总成本、配电网的总有功网损和储能峰谷套利收益及成本之和为目标函数，以功率平衡、节点电压、线路传输功率和储能能量平衡为配电网节点的约束条件来搭建数学模型。

1.1 目标函数

实际应用过程中，储能系统经济成本CES由初始投资成本Cinv、运维成本Com两部分成本组成，计算公式为：

初始投资成本是指储能系统工程初期建设所需投入的成本，一般用于主要设备的购买，由容量成本、功率成本两部分组成。容量成本是配备一定容量的储能系统所需成本，功率成本则是储能运行过程中所需要的辅助设备成本，例如电池储能系统初始投资就包含配置储能变流器PCS、能量转换系统BMS以及监控系统等装置成本。

式中，CE、Cp分别为储能系统单位容量和单位功率成本；CES、PES分别为储能系统额定容量和额定功率。

运维成本用于维持储能系统正常运行，包括系统的安装、试验、维护、检修、损耗等，当运维成本不易确定时，一般可根据初始投资的一定比例近似估算运维成本。

式中，Comp、Come分别为储能系统单位功率和单位容量运维成本。

考虑到资金的时间价值，将储能系统经济成本转换成等年值成本C，即：

式中，dr为折现率；T为系统寿命；为资金回收系数。

在采用分时电价的市场环境下，储能系统可通过在电价低谷时期进行充电，在电价高峰时期进行放电，从而达到平移负荷，实现峰谷套利，降低用电成本的作用。

峰谷套利收益具体可以表示为：

式中，PC(t)为t时刻的储能充电功率；PR(t)为t时刻的储能放电功率；p(t)为分时电价t时刻的价格；Δt为充放电时间，取1 h。

电网容量的无功损失系数是衡量配电网经济负荷运行指标的一个重要指标，当蓄电池储能系统接入配网后，可以显著地减少电网的有功损耗，从而使经济负荷运行评价指标也因此大大得到了提高。为使电网的潮流效应和降低电网损耗，文中提出了以电网损耗变化量最小为目标的方法，也就是当网损的变化数值最小时，网损达到最小，其数学公式如下：

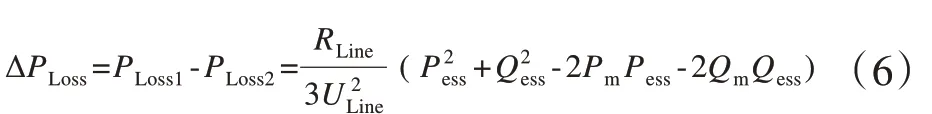
式中，PLoss1为储能接入后的有功网损；PLoss2为储能接入前的有功网损；RLine为线路电阻；ULine为线路电压；Pm、Qm分别为负荷侧的有功功率和无功功率；Pess和Qess分别为储能装置的有功功率和无功功率。

综合考虑了储能系统经济成本、峰谷套利收益和有功网损这三个重要指标，储能装置的配置优化设计的目标函数是

1.2 约束条件

1）功率平衡约束

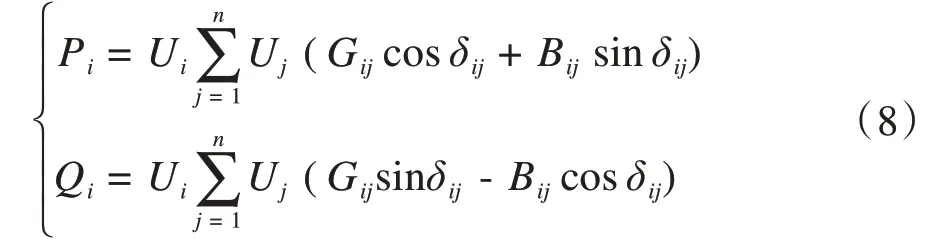
式中，Pi、Qi分别为i节点有功和无功功率；Ui、Uj分别为i、j节点电压幅值；n为系统节点数；Gij、Bij分别为节点导纳矩阵元素实部、虚部；δij为i、j节点电压相角差。

2）电压约束

式中，Umin为节点电压下限值；Umax为节点电压上限值。

3）储能能量平衡约束

式中，TC、TR分别为储能充、放电时间。

4）线路传输功率约束

式中，Pij为线路i、j之间的传输功率；Pij.max为线路i、j之间的最大传输功率。

2 粒子群优化算法

粒子群优化算法基于鸟群觅食行为，通过模拟该行为规律求解优化问题。鸟在觅食时，会不断地调整自己与猎物的距离，从而增加觅食的机会，其最快找到食物的方式就是通过前往搜索过程中自身离食物最近的位置和其他觅食同伴离食物最近的位置向食物靠近，同理粒子群寻优主要依靠个体最优值和群体最优值。

粒子有三个特性：速度、位置和适应度值fitness。而适应度的大小，则是由目标函数来求出，这是衡量颗粒强度的重要指标。经过初始化的微粒群在最优解的区域内移动，并根据自身与个体极值Pbest、群体极值Gbest的距离，不断地调整自己的速度和位置，逐步逼近极限。在此基础上，个体的极值是指在一个特定的最优解的范围内，通过搜索，可以获得最好的种群适应性，而种群的极值是指，在一个特定的种群或种群系统中，几乎所有的单个颗粒都可以在它的最有效解范围内进行搜索，从而获得较好的种群适应性。根据粒子的位置不断地更新，可以根据粒子的适应值、个体极值和群体极值的变化来测量。

假定一个种群是在某一个D维的解空间中，种群X=（x1，x2，…xn）由n个粒子构成，D维解空间群中的每一个粒子i的空间相对空间位置可用向量xi=（xi1，xi2，…xiD）T，i=1，2，…，n表示，通过求出各粒子的目标函数，求出各粒子xi适应度值fitness。用vi=（vi1，vi2，…viD）T表示第i个粒子的速度，各个粒子的个体极值为pi=（pi1，pi2，…piD）T，群体极值为gi=（gi1，gi2，…giD）T。

粒子的速度和位置随着迭代次数的增加不断变化，更新公式可表示为：

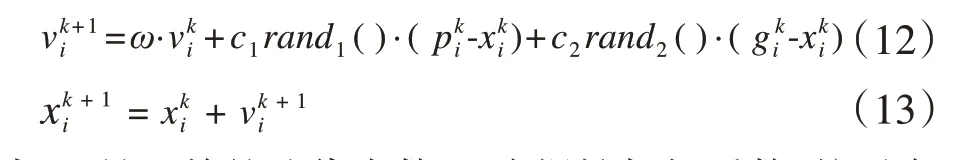
式中，k是目前的迭代次数，ω为惯性加权系数，粒子自我学习的因子为c1，粒子社会学习的因子为c2，rand1()和rand2()是在（0、1）间分布的一个随机数。在粒子速度的公式（12）中，含有三个随机成分，其中第一个成分表示粒子的初始速度，随着参数ω的增大，粒子的初始速度也随之增加。第二个分量代表了目前各微粒的最佳适应度，并对各微粒进行了优化，如果第i个粒子发现了比其它粒子更好的解决方案，则个体极值更新。自我学习因子c1对第二阶段的更新有一定的影响，所以第二阶段是“自我学习”。第三个分量代表所有粒子中最佳适应度值，将各微粒的极值保存下来，并对各微粒gki的优劣进行比较。社会学习因子c2的取值对第三部分的更新有一定的影响，因此第三个分量是“社会学习”。

图1详细给出了迭代过程中第k次和第k+1次的粒子速度和位置更新示意图。图中，v1、v2、v3、v（k）、v（k+1）分别表示式（12）中的五个分量，它们共同作用，决定了粒子在运动过程中的初始速度和它们的相对位置。

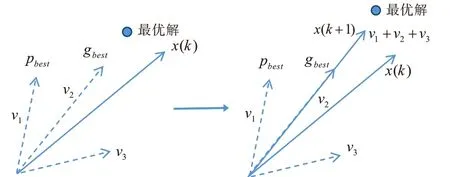
图1 粒子的位置与速度更新示意图

对粒子进行初始化时，会设定粒子的速度和位置范围，但在算法运行过程中，粒子更新后速度、位置取值可能会不满足设定要求，所得最优解亦不满足要求。确保结果的有效性，有必要对粒子进行边界约束，使将要超出或已经超出边界的粒子返回设定范围内，并赋予其一个相反的速度方向，确保后续取值满足设定要求，从而继续搜索最优值。其算法流程如图2所示。

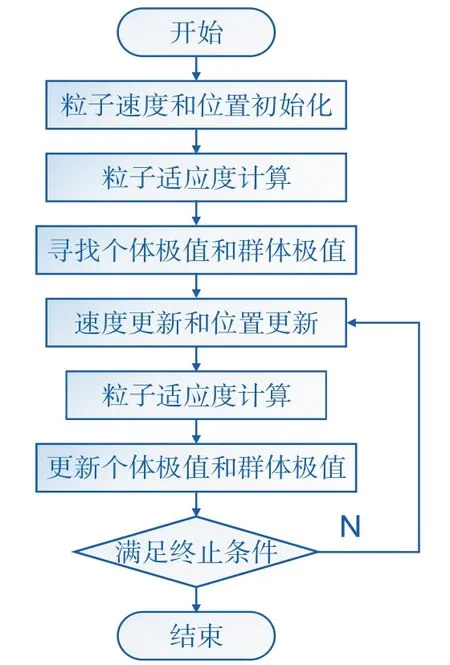
图2 粒子群算法流程图

3 算例分析

以南昌市新建区一条10 kV配电线为实例，开展储能配置优化计算分析。算例馈线载流量550 A，额定容量10 MV·A，供区内存在县域居民、执法大队、养殖场、贸易公司等多类负荷，区域电网有待进一步建设，馈线的等效拓扑如图3所示。

图3 线路网络拓扑

选取夏季气温较高的某一个工作日为典型日，其负荷波动曲线见图4，设定电网中储能系统允许接入节点为2-19，接入节点数为2个；储能系统容量成本为1 000元/kW·h，功率成本为1 200元/k W，储能系统寿命为20年。

图4 典型日负荷波动曲线

以接入两节点的储能系统功率、容量大小为变量，以网络有功网损、储能系统经济成本和峰谷套利收益为目标函数，设置粒子群种群大小为100，惯性权重系数w设置为0.7，加速因子c1=c2=2.05，多次改变储能接入节点，最终综合考虑选定节点6，15作为储能接入节点，接入位置及其接入容量如下表1所示，此时储能的经济成本为516.22万元，峰谷套利收益为607.6元/d。在实际应用过程中，应根据节点实际地理环境、可接入条件等确定其是否可接入储能系统、可接入储能类型，储能配置容量最小精确值与其储能类型单体容量大小有关。

表1 接入位置与容量

图5是配置储能前后的有功网损变化曲线，充分表明储能加入后网络损耗大大降低，有利于电网更经济地运行；图6是配置储能前后的0：00各节点电压图，表明储能的接入可以有效地提高各节点电压，从而提高了整个配电网的电压水平，保证配电网高可靠性供电。可见，如果分布式储能装置的接入作用的时间是长期的，其可为配电网带来可观的收益。

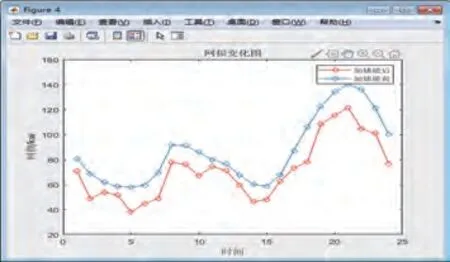
图5 储能配置前后有功网损变化曲线

图6 储能配置前后0:00时各节点电压图

从实例计算分析结果可以得出，在电网建设过程中，配置储能对提高配电网电压水平，降低电网有功网损有较为显著地效果，文中所使用的优化算法对工程实际应用有着较好的应用效果，在投资建设储能之后可以利用储能峰谷套利降低电网建设成本，同时，还可以到达促进新能源消纳，加快双碳目标的实现的目的。另外，在粒子群寻优过程中，出现某些节点接入储能后系统稳定指标值比未接入储能时更大的情况，系统稳定性下降，在花费大笔配置费用后却对系统造成不好的影响，可见在合理位置接入储能的的重要性。

4 结语

文中采用网络有功网损、储能系统经济成本最小作为目标函数，考虑了储能装置的峰谷套利收益，以南昌市新建区一条10 kV配电线为实例，较全面地对配电网储能系统进行了优化配置，从计算分析结果可以看出选取合适容量的储能装置，在合适的位置接入，可以有效地降低网络损耗并且减少电压偏移。加入储能装置后，使得电力系统的稳定性与可靠性上升了，长期来看还降低了电网的建设成本。这说明文中所使用的优化算法对于配电网中储能的配置优化具有可行性和可操作性，达到了储能配置优化较好的应用效果，对实际电网建设有较好的实际意义。