基于长短期记忆网络的动车组轴箱轴承故障诊断预测模型研究*

刘冠男 常振臣 高明亮 赵 明 高 珊

(中车长春轨道客车股份有限公司国家轨道客车工程研究中心， 130062， 长春∥第一作者， 正高级工程师)

据统计，动车组转向架故障中，由轴箱轴承失效导致的故障占到了45%～55%[1-4]。因此，动车组轴箱轴承早期故障诊断预测显得尤为重要。传统的轴承故障诊断方法主要是通过信号处理技术，经滤波解构，将能够反映设备运行状态的目标信号从含有众多噪声的原始信号中提取出来，然后通过建立近似的物理模型再加以相应的数值计算，将目标信号进一步分析和还原，以精准地确定故障状态及故障点位。该方法在数据不多、情况不复杂、环境较好、误差不大的条件下的试验结果尚能达到预期，但由于转向架轴箱轴承数据所呈现的特性，这种传统的、依靠信号分析技术解构信号、依靠数据分析提取特征的故障诊断方法的缺点也逐渐被扩大。随着计算机计算能力的增强，神经网络、深度学习算法开始为大众所知。与传统的故障诊断算法不同，新兴的深度学习的故障诊断算法拥有极强的特征提取能力，善于提取数据内部隐含的特征并且不依赖于人工的力量[5]，可以实现算法的自主学习。

动车组的故障诊断预测模型是通过系统传感器的检测数据来构建的，该过程是一个时序高维问题[6-9]。并且转向架轴箱轴承数据呈现出异构性、海量性、多样性等特点，对故障诊断技术的鲁棒性、实时性、泛化能力等提出了新的要求[7]。本文以深度学习理论为基础，以转向架轴箱轴承为研究对象，结合轴承故障诊断等相关理论，将深度学习理论应用于轴承故障诊断领域的尝试和探索。通过LSTM(长短期记忆网络)构建故障诊断分类模型，自主获取不同工况下轴承振动信号的特征，最终达到可以准确地识别各类轴承故障的目的。LSTM深度学习理论与故障诊断在实际的生产和生活中相结合，不仅可以推动算法理论进一步的完善，更能够精准地预测轴承的运行状态及故障情况，实现对转向架轴箱轴承的预防性维护[10-12]。

1 LSTM的深度学习

LSTM专门设计用于精确地模拟时间序列及其长期依赖性，且其反馈回路架构比其他神经网络在模式识别上更胜一筹。与其他RNN(递归神经网络)架构相比，LSTM可以解决传统的RNN中存在的梯度消失和梯度爆炸等问题，拥有比传统RNN更好的长短期记忆性能。LSTM与其他神经网络的主要不同之处在于LSTM基本单元的内部设计及LSTM 架构的变化。LSTM具有学习长期依赖性的能力和优秀的模型结构，因此更适用于基于时序序列诊断预测的轴箱轴承分类问题。

1.1 LSTM结构

长短期记忆体的结构由具有自重为1.0的自连接的线性单元组成。保留流入此自循环单元的值(正向传播)或梯度(反向传播)，并随后在所需的时间步长中进行检索。通过时间步长使得上一个时间步的输出或误差与下一个时间步的输出或误差相同。该自循环单元，即存储单元，能够存储过去几十个时间步的信息，这对于多任务学习而言非常强大。例如，针对轴承振动数据，LSTM单元可以存储前一时间段中包含的信息，并将此信息应用于当前阶段的诊断。

如图1所示的LSTM结构可见，每个LSTM块都具有4个神经网络层，且该4个神经网络层会以特殊的方式相互作用，使LSTM完成一系列的记忆、遗忘等动作。

注：Xt为t时刻状态下数据的输入;ht为t时刻接收到的上一个节点的输入;σ为当前节点状态下的权重值;tan h为激活函数；“+”为数据矩阵相加，“×”为数据矩阵相乘。图1 LSTM结构图Fig.1 Diagram of LSTM network structure

LSTM结构的关键就在于其单元状态(见图2中的黑色加粗线条)。该单元状态顺着整个LSTM链条从头运行至尾，期间与其他信息交互很少，其上所运载的信息可以在长时间内保持不变，这就是LSTM可以学习长期依赖性的原因。

LSTM通过一种名为“门”的结构来实现信息的记忆(增加)和遗忘(删除)。在某些情况下，需要利用更新的、更相关的信息代替存储单元或单元状态中的信息，因而希望丢弃旧的、过时的信息。同时，不希望通过将不必要的信息发布到网络中来混淆其他的循环网络。为了解决此问题，LSTM单元具有一个遗忘门，遗忘门会删除自循环单元中的信息，从而为新的存储器腾出空间。该做法不会将信息发布到网络中，从而避免了可能的混乱。遗忘门通过将存储单元的值乘以0(全部删除)和1(保留所有内容)之间的数字来完成此操作，具体值由上一个时间步的当前输入和LSTM单位输出确定。

注：Ct为t时刻状态下数据的输入； ft为t时刻输入门的输出；it为t时刻遗忘门的输出；ot为t时刻输出门的输出。图2 LSTM结构细节图Fig.2 Details of LSTM structure

在其他时间内，存储单元包含需要保留许多时间步长的值。为此， LSTM模型添加了另一个门，即输入门或写门，可将其关闭，以便没有新的信息流入存储单元。这样，存储单元中的数据将得到保护，直到需要它为止。

输出门通过将存储单元的输出乘以0(无输出)和1(保留输出)之间的数字来操纵存储单元的输出。

双向LSTM通过允许未来数据为时间序列中的历史数据提供信息，可以提高LSTM网络的性能。与简单的前馈网络相比，这类LSTM网络可以更好地解决复杂的序列学习或机器学习问题。

1.2 LSTM原理

LSTM原理如下：

第1步，在LSTM中确定需要从单元中遗忘的信息，这个动作由“遗忘门”完成。“遗忘门”以ht-1和xt为输入；在Ct-1单元中输出1个[0,1]范围内的数，其中1代表完全保留，0代表完全遗忘。

ft=σ(Wf·[ht-1,xt]+bf)

(1)

式中：

Wf——t时刻输入门的权重值；

σ——LSTM的传递函数；

bf——遗忘门的阈值。

第2步，LSTM需要确定记忆(存储)的信息。这个动作由两部分组成：先将ht-1和xt输入至名为“输入门”的神经网络层，由该神经网络层确定存储到LSTM内的值；然后创建1个候选向量，该候选向量由tanh层创建，用于加入状态机中。

it=σ(Wi·[ht-1,xt]+bi)

(2)

Ct，s=tanh(WC·[ht-1,xt]+bC)

(3)

式中：

it——t时刻记忆门的输出；

Ct,s——t-1时刻的输入与t时刻的输入叠加的输出；

Wi——LSTM的权重值；

bi——i时刻记忆门的阈值；

WC——i时刻记忆门的权重值；

bC——i时刻输出门的权重值。

第3步，采用更新的、更进步的、更相关的单元状态Ct去替换旧的、落后的、不相关的单元状态Ct-1。将旧的状态乘以ft，通过该动作，可以遗忘LSTM在第1步中决定所舍弃的或许是过时的或错误的信息；接着在此基础上加上itCt,s，其中，itCt,s是新的候选值。根据操作者决定更新每个状态的程度进行变化。

Ct=ftCt-1+itCt,s

(4)

最后，决定LSTM要输出的内容。单元状态决定了其输出值的类型，但并非单元状态中的所有信息都是要输出的。因此，需要利用Sigmoid神经网络层来决定单元状态的去和留。将经过压缩处理的单元状态与Sigmoid层的输出相乘，从而得到最终值。

ot=σ(Wo[ht-1,xt]+bo)

(5)

ht=ottanh(Ct)

(6)

式中：

Wo——t时刻输出门的输出权重值；

bo——t时刻输出门的输出阈值；

ot——t时刻输出门的输出值；

bi——t时刻输出门的输出权重值。

2 基于LSTM模型的轴箱轴承故障诊断方法

2.1 轴承故障试验数据集预处理

2.1.1 数据集1预处理

本文选取的2个数据集均来源于网络开源数据集。数据集1中轴承故障检测训练赛所利用的数据(以下简为“竞赛数据集”)，共有训练集和测试集2个文件。其中，训练集中的数据一共有792行、6 002列：第1列是数据编号，第2列到第6 001列是轴承的振动数据，最后1列代表了对应这一行数据的轴承的故障类型。除正常状态外，轴承故障类型一共有9种，因此轴承共有10种状态，如表1所示。

轴承故障数据共528行、6 001列。前6 001列故障数据与训练集中前6 001列故障数据的含义相同，在结构上仅缺少最后1列标签列。利用该数据集中的数据作为神经网络的训练数据集，并在轴承的简易故障检测系统运行时，通过已训练好的模型预测样本集中的数据，并将结果加以展示。

表1 竞赛数据集的轴承故障标签表Tab.1 Bearing failure tag table of the competition data set

数据输入预处理过程如下：先将故障源文件中的数据读取到模型数据结构中；再将全部数据按第1列到6 001列及第1列到第6 002列，分为振动信号数据(X)和标签数据(Y)；为了保证模型在训练时的准确度和损失值在正常范围内，将振动信号数据和标签数据分别归一化；按训练集与测试集为7∶3的比例，将全部数据分为训练集和测试集。

2.1.2 数据集2预处理

数据集2是动车组轴承实验室所提供的数据(以下简为“动车组数据集”)。该数据集包含了轴箱轴承在多达数十种工况下的数据。根据轴承数据，振动数据的采样频率为25 600 Hz，温度数据的采样频率为1 Hz。本文中该数据集的采集频率取48 kHz，则该工况下的轴承转速为1 797 r/min，驱动端轴承故障数据共有9种故障和1种正常状况。9种故障状况分别为3种不同损伤直径下的内圈故障、外圈故障和滚动体故障。其中，外圈故障的故障点均在6点钟方向。动车组数据集如表2所示。

表2 动车组数据集Tab.2 Data set of EMU

数据输入预处理过程如下：利用深度学习预处理文件中的函数，将动车组数据集中的数据整理为1 000组长度均为6 000的振动信号，并对每组数据赋予相应的标签，再按一定比例分为训练集、验证集和测试集。

2.2 基于LSTM模型的轴承故障诊断预测流程

LSTM处理序列数据的神经网络具有巨大优势，可直接将振动时域信号作为模型网络的输入层。基于LSTM模型的轴承故障诊断预测流程如图3所示。

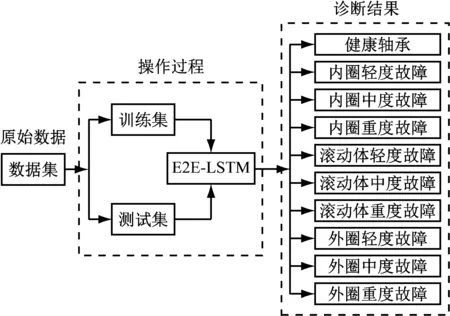
注：E2E为端到端。图3 基于LSTM模型的轴承故障诊断预测流程框图Fig.3 Flow chart of bearing fault diagnosis prediction based on LSTM model

基于LSTM模型的轴承故障诊断流程如下：

1) 数据预处理。将全部数据按一定比例划分为训练集和测试集，利用训练集中的数据对模型进行训练，修改数据输入格式，对原始数据进行截断、重新组合，使其适配模型。

2) 特征提取。将预处理后的振动时域数据作为LSTM网络的输入，进行特征学习，并确定基于振动数据的LSTM迭代次数、隐藏层层数及其他参数。

3) 故障诊断。将训练好的LSTM网络的输出层连接在一起形成全连接层，最后采用Softmax分类器对振动信号进行分类，实现故障诊断。

4) 保存模型。将模型保存至指定路径，后续供系统进行调用。

2.3 试验验证

为发挥LSTM善于处理时序序列问题的优势，以及解决数据长度对于LSTM模型而言计算复杂的问题，本文将振动数据按照批次分步输入LSTM模型进行训练。利用宽度固定的滑动窗口，窗口长度为150，每次截取150个数，重叠率为50%，即每次截取的数据与上次截取的数据有50%是相同的。以此计算，将1组数据中6 000个数分为79步输入至LSTM模型中。构建的LSTM结构如图4所示。

注：6 000×1代表输入数据的维度；150代表输入层数。图4 LSTM结构图Fig.4 Diagram of LSTM network structure

按照已设定的输入格式，确定LSTM模型的结构。本文所构建的LSTM模型由LSTM层、全连接层和输出层组成。其中，第1层的LSTM层的数据输入格式设置为(79，150)，即该层含有79个时间步，每次输入数据长度为150；LSTM层中的神经元数设置为128；输出层根据不同问题设置不同数值，该问题中的分类数为10，因此输出层中的变量设置为10。

设置好LSTM模型的结构之后，设置训练参数。训练参数包括轮次、批次和迭代次数。迭代即为利用指定数量的数据完成一次正向传播及反向传播，并更新模型参数的过程；批次即为完成一次迭代利用数据的组数；轮次即为训练集中的数据全部完成一次正向传播和反向传播。试验结果表明，轮次的设置要尽量大，使得训练集及测试集或者验证集中数据的准确率和损失函数的曲线达到相对平稳。批次的设定要根据算法的实际运行情况进行调整，若批次取值较小，则每一轮训练迭代次数较多，导致计算速度慢，但参数的调整快；若批次取值较大，则每一轮的迭代次数较少，导致计算速度快，网络的梯度亦更加准确。通过反复测试，最终确定批次设置为64，轮次设置为200。

本文首先利用竞赛数据集进行模型的训练，将竞赛数据集分为训练集和测试集。在每轮训练完成之后，利用测试集中的数据作为验证集对模型进行验证。该步骤的目的是为了防止模型的过拟合，通过模型在测试集上的准确率和损失函数进行判断，从而再去调整模型的参数，以达到最好的效果。LSTM利用经过竞赛数据集训练200轮的结果如图5所示。从图5可以看出，在训练进入大约20轮之后，模型在训练集上的准确率和损失函数就已经达到一个稳定的状态，且准确率达到了100%，损失函数也趋近于0；在训练进入约120轮之后，模型在测试集上的准确率和损失函数也不再改变，准确率达到0.980左右，损失函数则在0.077左右。

图5 竞赛数据集LSTM训练损失值及准确率Fig.5 LSTM training loss value and accuracy rate of the competition data set

本文利用动车组对该模型进行训练，模型结构参数及训练参数的设置需要进行一定的修正，以使模型更好地契合第2个模型数据集。经过反复测试最终确定将输入数据格式修改为39个时间步，每次数据输入长度为300；将批次修改为256，将Epoch设置为200，同时增加1层神经元为128个的LSTM层。修正后模型的训练结果如图6所示。由图6可知，训练接近60次时，模型在训练集和验证集上的准确率和损失函数就已经几乎保持不变，验证集的准确率稳定在0.997。通过模型评价函数，采用已完成训练的模型对测试集进行评价，其准确率为0.875。

图6 动车组数据集LSTM训练准确率Fig.6 LSTM training accuracy rate of EMU data set

3 结语

本文充分利用动车组轴承振动信号时间序列的特点，以及LSTM擅长处理时间序列的优势，构建LSTM模型对轴承的故障状态进行识别，并采用LSTM算法对转向架轴箱轴承进行故障诊断。模型的仿真和试验表明，该诊断模型能有效地提高故障诊断的辨识精度,模型拟合优度达到99%，辨识正确率最高达到87%。该研究成果可有效提升动车组轴承运用、维修及管理水平,具有良好的应用前景。