一种改进的基于深度神经网络的偏微分方程求解方法*

陈新海,刘 杰,万 仟,龚春叶

(1.国防科技大学并行与分布处理国家重点实验室，湖南 长沙 410073；2.复杂系统软件工程湖南省重点实验室，湖南 长沙 410073)

1 引言

随着计算能力的提升，数值分析在诸多科学与工程领域发挥着越来越重要的作用[1]。大部分数值分析问题的底层数学模型都可以归结为对偏微分方程的数值求解。传统的数值求解方法主要包括有限差分法、有限元法和有限体积法[2]。这些方法首先将计算域离散为独立的网格单元，然后在单元子域上迭代求解偏微分方程系统，以此获得未知函数的数值近似解。然而，为了保证数值分析的准确性和有效性，传统方法通常十分耗时且强依赖人工经验：一方面，迭代求解大型线性/非线性方程组需要昂贵的计算开销；另一方面，为了避免计算失效，通常在网格剖分阶段还需要频繁的人机交互来判别和优化计算网格的质量，以满足求解器和模拟精度的要求[3,4]。随着所分析的问题越来越复杂，繁重的交互和开销限制了传统数值求解方法在实时模拟、气动参数设计和优化空间探索等问题上的应用效率。

近年来，以深度神经网络为代表的人工智能技术取得了令人瞩目的突破和成果。以往的研究已证明，深度神经网络是复杂知识系统和函数拟合的有效替代[5,6]。通过训练由神经元组成的深度神经网络，其模型能够从高维的非线性空间中学习到潜在的规则和特征，最终拟合得到输入与输出之间的函数映射关系。深度神经网络在各个领域的应用被认为是“解放劳动力”的过程[2]。受启发于深度神经网络在图形图像、自然语言处理等领域的广泛应用，深度学习方法越来越多地应用到受限于高额计算开销和领域人工经验的数值分析中。

Chen等[7,8]证明了神经网络的万能逼近定理，即由包含非线性激活函数(如Tanh、ReLU、Sigmoid激活函数)的隐藏层构成的前馈神经网络能够近似任何从一个有限维空间到另一个有限维空间的Borel可测函数。该定理随后被进一步推广到了微分算子的近似，为使用神经网络求解偏微分方程奠定了理论基础。基于该理论，Malek等[9]提出了一种求解高阶微分方程的混合神经网络模型，该模型使用了Nelder-Mead方法来构造常微分方程的封闭解，并在微分方程的初始/边界值问题上取得了很好的效果。Mall等[10]通过构造满足边界条件的损失项和神经网络模型，提出了一套求解常微分方程的回归算法，同时还研究了神经元数量和初值对预测解精度的影响。但是，这些方法都只适用于常微分方程求解。

Lagaris等[11]提出了适用于不规则边界的基于神经网络的偏微分方程求解模型，该模型使用多层感知机和径向基神经网络来拟合复杂边界，并在一些较为简单的二维、三维偏微分方程上取得了较高的预测准确率。Sirignano等[12]提出了基于长短时记忆LSTM(Long Short-Term Memory)网络的偏微分方程求解方法，用于求解高维的偏微分方程。但是，以上方法都只适用于特定类型的偏微分方程，缺乏一定的通用性。2019年，Raissi等[13]提出了物理信息神经网络PINN(Physics-Informed Neural Networks),用于近似偏微分方程中的待求解函数。该方法利用深度神经网络的函数拟合能力，用控制方程组和边界函数来约束网络中可调参数(权重和偏置)的迭代更新过程，最终得到输入的时空点坐标到待求函数的端到端映射模型。整个求解过程不需要进行网格离散以及先验的数值求解，且训练后的模型能够在极小计算开销下自动预测计算域内任意点的观测值，这大大提高了数值分析的效率。但是，传统的物理信息神经网络在求解许多基于偏微分方程的物理问题时存在预测精度低的情况。

为了进一步提高物理信息神经网络方法在求解实际问题时的准确性，本文提出了一种改进的基于深度神经网络的偏微分方程求解方法TaylorPINN。与传统PINN中直接使用回归模型输出离散的预测值不同，TaylorPINN利用深度神经网络的函数逼近能力，并结合泰勒公式，通过构造解的形式将神经网络输出与待求函数联系起来，实现了无网格的数值求解过程。在Klein-Gordon方程[14]、 Helmholtz方程[15]和Navier-Stokes方程[16,17]上的数值实验结果表明，TaylorPINN能够准确拟合计算域内时空点坐标与待求函数之间的映射关系，并提供了准确的数值预测结果。与常用的基于物理信息神经网络方法相比，对于不同数值问题,TaylorPINN将预测精度提升3～20倍。

2 理论背景介绍

2.1 偏微分方程

为方便讨论，设偏微分方程的一般形式如式(1)所示：

(1)

其中,D表示微分算子，u是待求解的函数，计算域Ω⊂Rd。方程(1)的边界条件定义如式(2)所示：

B[u(x,t)]=h(x,t),x∈∂Ω

(2)

初始条件如式(3)所示：

(3)

2.2 物理信息神经网络PINN

2019年，Raissi等[13]提出了物理信息神经网络PINN的概念，即用深度神经网络模型来求解偏微分方程控制的物理问题。在PINN中，偏微分方程的数值解问题被转化为基于神经网络的最优化问题，并通过搭建深度神经网络u(θ)作为黑盒回归模型来拟合待求的函数u。在网络训练优化过程中，PINN只使用方程组本身的信息来约束神经网络参数的优化。具体地，用于指导优化的损失函数Loss由3部分组成，分别是方程残差项MSEu以及条件项MSEb和MSEI：

Loss=MSEu+MSEb+MSEI

(4)

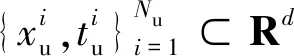
(5)

(6)

(7)

通过最小化损失函数Loss，PINN能利用神经网络的函数拟合能力得到同时满足方程项和条件项的待求解函数u的近似解u(θ)，即：

u≈u(θ)

(8)

该近似解由一个前馈神经网络表示，对于计算域中的任意点坐标，训练后的网络模型都能够通过几次矩阵乘高效地预测出对应的函数值，从而实现点坐标到物理场的端到端映射。基于PINN的训练和预测过程消除了对计算网格的依赖，大幅提高了数值分析的效率。但是，现有的物理信息神经网络在求解许多基于偏微分方程的物理问题时存在预测精度低的情况，从而限制了该方法的实用性和有效性。

3 基于深度神经网络的偏微分方程求解方法TaylorPINN

为了进一步提升物理信息神经网络的预测精度，本文提出了一种改进的基于深度神经网络的偏微分方程求解方法TaylorPINN。该方法同样将微分方程的求解问题转化为函数的最优化问题。但是，与传统的物理信息神经网络不同的是，TaylorPINN在预测过程中加入了对待求解函数的形式构造过程，即不再直接使用回归模型输出离散的预测值，而是通过构造解的方式将神经网络输出与待求解函数联系起来。在这个过程中，如何构造解的形式成为了问题转化后的关键。

泰勒公式是一种广泛用于函数逼近的方法，定理1是一元函数的n阶泰勒展开定理：

定理1设函数f(x)在x=x0的邻域内n+1阶可导，则对于位于此邻域内的任一点x有：

f(x)=f(x0)+f′(x0)(x-x0)+…+

(9)

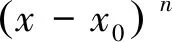
根据上述定理，本文采用基于泰勒公式的多项式函数空间来构造解的形式，即令偏微分方程中的每个待求解函数如式(10)所示：

(10)

相比于其他函数空间(如傅里叶级数或各类径向基函数)，由时空坐标(x,t)的线性加权及其乘积构成的多项式空间拥有灵活的扩展性，在拥有强的函数表达能力的同时也易于实现，且计算开销相对较小。

Figure 1 Architecture of TaylorPINN图1 TaylorPINN的整体结构

在模型架构方面，TaylorPINN除了使用全连接层外，还引入了一个输入增强层作为一种增强手段来扩大输入点坐标的维度。该增强层实现了一个基于时空点坐标(x,t)的离散线性映射φ，φ如式(11)所示：

(11)

此外，在损失函数构造方面，TaylorPINN引入了一个静态权重参数α1来平衡不同损失项对迭代收敛的贡献，使神经网络模型在训练优化阶段就能够更好地满足各损失项，从而更快地收敛到最优值。最终，TaylorPINN的损失函数如式(12)所示：

Loss=MSEu+α1(MSEb+MSEI)

(12)

图1显示了TaylorPINN的整体结构，其结构包含输入层、输入增强层、进行高维函数空间特征学习的隐藏层和最后的输出层。其中，TaylorPINN的输入层以计算域的时空点坐标为输入，在扩维后传播到由全连接层组成的隐藏层。前向传播得到输出值λ，作为基于泰勒公式的解形式中的系数来计算待求解函数的值。在训练阶段，得到的函数值用于计算损失函数的值及反向传播的梯度。在预测阶段，该输出值将直接用于计算待求解函数的预测解。TaylorPINN的训练过程如算法1所示。

算法1TaylorPINN训练过程

输入:计算域内的时空点坐标。

输出:训练后的TaylorPINN模型。

Step1分别从计算域内和边界随机选取时空点坐标，组成训练样本集。

Step2搭建TaylorPINN神经网络并根据待求解的偏微分方程构建损失函数Loss。

Step3初始化网络参数。

Step4随机从样本集中选取时空点坐标作为训练样本输入TaylorPINN。

Step5使用优化算法最小化损失函数Loss，并更新神经网络中的优化参数。

Step6重复步骤4和步骤5，直到完成预定的迭代轮数。

4 数值实验与分析

本节使用Klein-Gordon方程[14]、Helmholtz方程[15]和Navier-Stokes方程[16,17]3个数值案例来评估TaylorPINN的偏微分方程求解能力，并在相同网络结构、超参数及训练迭代轮数的条件下与传统PINN进行预测性能对比。实验中使用的初始学习率均为0.001，衰减率为每1 000轮衰减0.9，优化器选用Adam[18]，batchsize为128。实验的测试平台是Intel Core i7-6700和NVIDIA Tesla P100，实验环境是TensorFlow1.15.0[19]。偏微分方程中的微分项统一用TensorFlow中的自动微分函数“tf.gradient()”[20]。神经网络模型的预测精度使用L2误差来衡量，其计算方式如式(13)所示：

(13)

其中,uref是待求方程的参考解，通常由解析解或高精度数值解表示;upred是神经网络提供的预测解。为了保证实验结果的可复现性，本文将训练时的随机种子固定为666。

4.1 Klein-Gordon方程

在第1个测试案例中，本文使用Klein-Gordon方程来评估所提出方法的待求函数拟合能力。Klein-Gordon方程是量子物理、固体物理等领域的基础偏微分方程之一[14]。一维Klein-Gordon方程的形式如式(14)所示：

utt+αuxx+βuγ=q(x,t),

(x,t)∈Ω×[0,T],Ω=[0,1]

(14)

边界条件如式(15)所示：

u(x,t)=h(x,t),(x,t)∈∂Ω×[0,T]

(15)

初始条件如式(16)和式(17)所示：

u(x,0)=g1(x),x∈Ω

(16)

ut(x,0)=g2(x),x∈Ω

(17)

当设g1(x)=g2(x)=0,α=β=1,γ=3时，本文可以构造出方程的解析解作为神经网络预测的参考解，如式(18)所示：

uref(x,t)=xcos(5πt)+(xt)3

(18)

本文使用该解析解反推得到h(x,t)和q(x,t),用于后续计算损失函数中的残差项和条件项。对于偏微分方程(式(14)～式(17))，本文构建如式(19)所示的损失函数用于后续的神经网络训练：

(19)

Figure 3 Prediction results of TaylorPINN and PINN on Klein-Gordon equation图3 TaylorPINN和PINN在Klein-Gordon方程上的预测结果

在本案例中，本文搭建了一个包含3个隐藏层的TaylorPINN网络模型，每层神经元个数为100。在训练阶段，本文通过最小化损失函数来寻找最优的网络参数，以拟合Klein-Gordon方程的封闭预测解。本文令训练的总轮数为40 000轮，静态权重α1为10。测试集为计算域内均匀分布的10 000个时空点。不同泰勒公式阶数下，TaylorPINN的预测精度(L2误差)如图2所示。

Figure 2 Prediction performance of TaylorPINN on Klein-Gordon equation with different orders图2 不同阶数下TaylorPINN在Klein-Gordon方程上的预测性能

从图2中可以看出，随着阶数的增加，预测精度也逐渐增加，当阶数k=5时，模型实现了最佳的预测性能，L2误差为6.63E-03;但是，当继续增加泰勒公式阶数时，精度开始下降，其主要原因是由于阶数越大，输出层的神经元个数也就越多，对应模型收敛所需要的训练轮数、隐藏层宽度和深度也随之增大。因此，当固定模型结构和训练轮数后，TaylorPINN会在阶数较大时出现欠拟合的情况，从而影响模型收敛，导致预测精度下降。

图3和表1对比了PINN和TaylorPINN(k=5)在Klein-Gordon方程上的预测结果。其中图3a是由式(18)给出的参考解的可视化结果，图3b和图3d是由2个模型给出的预测解的可视化结果，图3c和图3e是参考解与预测解之间的绝对误差。从图3可以看出，TaylorPINN预测解与参考解基本吻合，且预测精度明显高于PINN的。从表1可以看到，在L2误差方面，虽然TaylorPINN在构建解的形式时会带来额外的计算开销，但相比于PINN,TaylorPINN将预测精度提升大约20倍。

Table 1 Comparison of the performance of TaylorPINN with PINN on Klein-Gordon equation

4.2 Helmholtz方程

在第2个测试案例中，本文使用TaylorPINN来求解二维Helmholtz方程。该方程在声学、电磁学和弹性力学等领域有着广泛的应用[15]。二维Helmholtz方程如式(20)所示：

Δu(x,y)+k2u(x,y)=q(x,y),(x,y)∈Ω

(20)

方程的边界条件如式(21)所示：

u(x,y)=h(x,y),(x,y)∈∂Ω

(21)

其中，Δ是拉普拉斯算子，计算域Ω为[0,1]×[0,1]。当k=1，源项q(x,y)如式(22)所示时，

q(x,y)=-π2sin(πx)sin(4πy)-

k2sin(πx)sin(4πy)

(22)

可以构建出方程的解析解,如式(23)所示:

uref=sin(πx)sin(4πy)

(23)

在TaylorPINN中，Helmholtz方程对应的损失函数如式(24)所示：

(24)

在本案例中，本文通过改变网络层数和单层神经元个数，测试了不同网络规模对TaylorPINN预测性能的影响。为了更好地分析不同规模下的性能结果，本文将TaylorPINN与相同规模下的PINN进行了比较。图4显示了当阶数为3，固定单层神经元数为50时，TaylorPINN在Helmholtz方程案例上的预测结果。

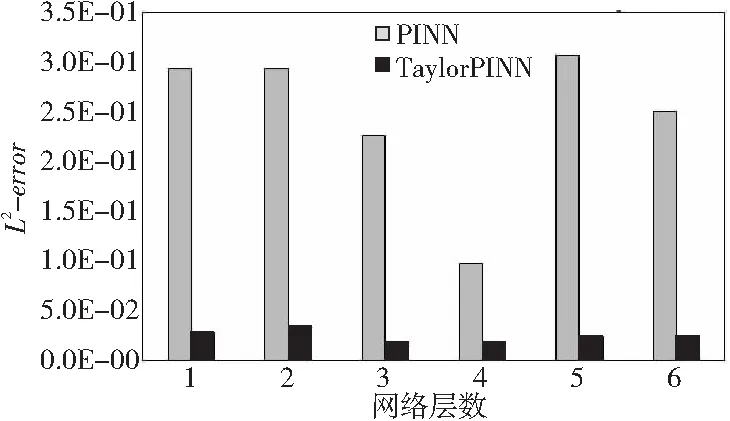
Figure 4 Prediction performance of TaylorPINN on Helmholtz equation with different numbers of network layers图4 不同网络层数的TaylorPINN在Helmholtz方程上的预测性能

从图4可以看出，当网络层数为3时，TaylorPINN实现了最佳的预测性能，其L2误差为1.86E-02。当继续增加网络层数时，预测精度反而会有所退化。但在不同网络层数下，TaylorPINN都获得了比PINN更高的预测性能，且预测精度最大可提升12倍。

表2显示了当固定网络层数为3，变化单层神经元数时PINN和TaylorPINN的L2误差。从表2可以看出，随着神经元个数的增加，2个网络模型都能得到预测精度提升。当单层神经元个数为50时，相比于PINN,TaylorPINN的预测精度提升了大约8倍，其可视化结果如图5所示。

Table 2 Influence of different numbers of neurons on the prediction performance of TaylorPINN

4.3 Navier-Stokes方程

在最后一个案例中，本文使用一个经典的流体力学案例——二维顶盖驱动流(如图6所示)[16,17]，来分析TaylorPINN的偏微分方程求解能力。

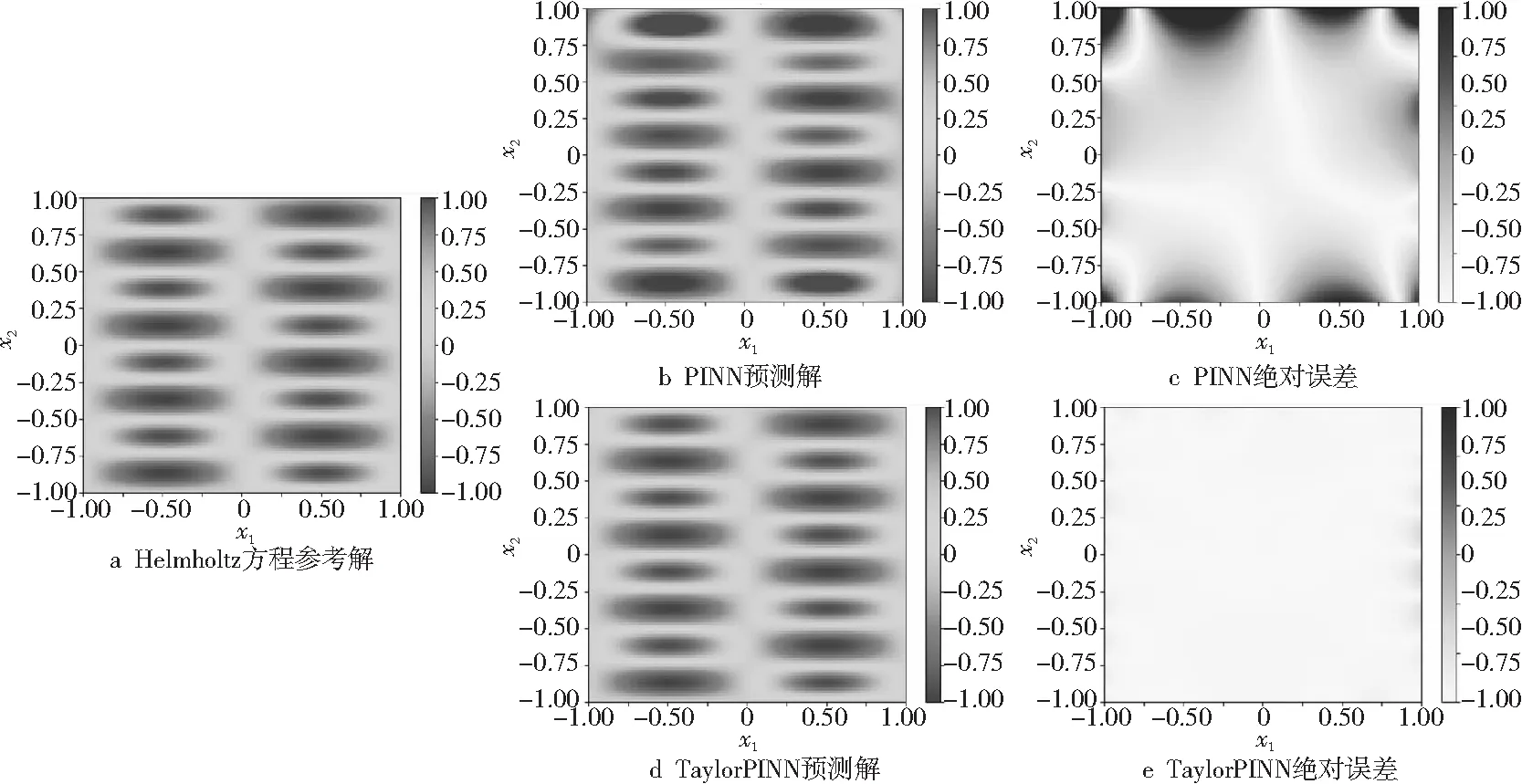
Figure 5 Prediction results of TaylorPINN and PINN on Helmholtz equation图5 TaylorPINN和PINN在Helmholtz方程上的预测结果

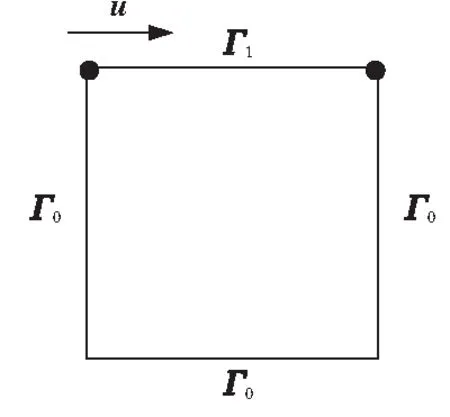
Figure 6 Lid-driven cavity flow case图6 顶盖驱动流案例

该案例的控制方程为不可压Navier-Stokes方程，如式(25)所示：

(25)

(26)

u(x,y)=(1,0),(x,y)∈Γ1

(27)

u(x,y)=(0,0),(x,y)∈Γ0

(28)

其中，u表示待求解的速度矢量场;p是标量压力场;Re是流体的雷诺数;计算域Ω为[0,0.1]×[0,0.1];Γ1是方腔的顶盖边界，其x方向速度分量为1 m/s;Γ0是其他3个边界，速度分量均为0。本文使用OpenFOAM[21]计算的该案例的数值解作为参考解。

在TaylorPINN的训练过程中，本文使用Navier-Stokes方程的涡量-速度形式VV(Vorticity-Velocity)来构建损失函数，在该形式下，u的速度分量(u,v)可以使用函数ψ来计算,如式(29)所示：

(29)

根据式(29)，方程自然满足不可压流体的连续性。此外，本文还去掉了时间项来进一步简化模型。最终构造的用于训练的Navier-Stokes方程损失函数如式(30)所示：

Loss=

(30)

根据边界条件的定义，对于Γ1上的采样点，h1(x,y)=(1,0),对于Γ0上的采样点，h0(x,y)=(0,0)。值得注意的是，该案例给定的边界条件在方腔的2个边界交界处(见图6中的黑色标记点)形成了不连续的奇点，即左右边界条件给定的交界点处的速度值为0，而上顶盖将交界点处的速度赋值为1。这种不连续性会影响神经网络的训练优化。因此，在本案例的样本点随机选取过程中，本文避免使用这2个间断点用于网络训练。

最终，本文搭建了一个包含3个隐藏层(单层神经元个数为100)的TaylorPINN。图7展示了当Re为100，泰勒展开式阶数为5时，TaylorPINN和PINN在顶盖驱动流案例上的预测结果。从图7可以看出，相比于PINN，TaylorPINN能够更准确地捕捉到流体流动的状态。表3中的结果显示，TaylorPINN在该案例上实现了7.76E-02的预测误差，而相同网络规模下PINN的L2误差为4.17E-01。

Figure 7 Prediction results of TaylorPINN and PINN on Navier-Stokes equation图7 TaylorPINN和PINN在Navier-Stokes方程上的预测结果

5 结束语

随着人工智能理论和技术的发展，使用深度神经网络技术提升传统数值分析的效率成为了当前学术界的研究热点。偏微分方程求解是数值分析的计算核心，本文提出了一种基于深度神经网络的偏微分方程求解方法TaylorPINN。该方法结合了神经网络和泰勒公式的函数拟合能力，实现了无网格的高效数值求解过程。在不同偏微分方程案例上的数值实验结果表明，TaylorPINN能够很好地拟合计算域内时空点坐标与待求函数值之间的映射关系，并提供准确的数值预测结果。在未来的工作中，考虑在网络模型上做进一步研究，例如将注意力机制引入网络模型，从而提高模型的准确率；也会改进提出的方法并将其应用到更复杂的物理问题场景中，以进一步增强该类方法的实用性。

Table 3 Comparison of the performance of TaylorPINN with PINN on Navier-Stokes equation