不饱和聚酯包覆层流动及浇注的仿真模拟
2022-11-17张豫鲁刘奔奔陈国辉曹贝贝何吉宇李向梅杨荣杰
张豫鲁,刘奔奔,陈国辉,曹贝贝,何吉宇,李向梅,杨荣杰
(1. 北京理工大学材料学院,北京 100081;2. 北京航空航天大学前沿科学技术创新研究院,北京 100191;3. 西安近代化学研究所,陕西 西安 710065;4. 北京理工大学化学与化工学院,北京 100081)
0 引言
包覆层用于对固体火箭推进剂的药柱进行包覆,可起到耐烧蚀、限燃、保证固体火箭推进剂正常工作的作用。近年来,随着固体火箭推进剂技术的发展,对装药包覆层的要求也越来越高,为了改善和提高包覆层的各项性能,较多文献报道了改性环氧树脂、硅橡胶、三元乙丙橡胶(EPDM)、聚磷腈包覆层的制备及性能研究[1-5],不饱和聚酯(UPR)由于其良好的力学性能、优异的加工性能和良好的抗迁移性而在包覆层应用中备受青睐。目前对UPR 包覆层的研究主要集中于UPR 包覆层的性能和应用方面[6-8],而关于UPR 包覆工艺的研究较少,实际浇注包覆过程中工艺参数的选择关乎到固体推进剂包覆过程的工艺安全性和包覆质量。具体而言,包覆浇注过程中树脂的粘度、流动性、温度、压力、浇注速度等都会影响包覆层的质量控制,从而影响到推进剂的质量和工艺安全性,因此有必要对UPR 包覆层浇注过程进行深入研究。
对浇注过程进行模拟仿真,可以大大减少重复试验的次数、优化包覆工艺、提高包覆效率和质量。Mitani等[9]建立模型模拟环氧树脂的流动,使用有限元方法模拟了环氧树脂在重力下的非等温和反应流动行为,且该模型不仅可以用于环氧树脂的流动模拟,也可以用于模拟其他热固性树脂的成型过程;王庆涛等[10]通过PAM-RTM 软件模拟比较了树脂转移模塑成型(RTM)和真空辅助树脂转移模塑成型(VARTM)2 种工艺,研究了不饱和聚酯树脂粘度、压力对成型灌注过程的影响;杨进水等[11]对UPR 固化过程中的流变特性进行研究,在修正双Arrhenius 模型和工程粘度模型的基础上建立了流变模型,并预测了低粘度工艺操作窗口;Kiehl 等[12]研究了碳酸钙填料含量不同时的UPR 的流变性能,得到了不同碳酸钙含 量UPR 的 粘 度-静 置 时 间 关 系;Aktas 等[13]模 拟 了UPR 在真空浇注过程中的粘度变化,将实验在不同温度条件下重复,得到了粘度-时间-温度曲线;张曼曼等[14]研究了UPR 在动态升温及恒温条件下的粘度变化,建立了工程粘度模型,并使用建立的模型预测了适用于真空辅助成型工艺的低粘度工艺窗口;刘奔 奔 等[15]采 用Carreau 模 型 建 立EPDM 的 流 变 特 性方程,并使用Moldflow 软件模拟EPDM 包覆层的注射成型过程。已有的研究成果表明,热固性树脂的流动过程是较为复杂的过程[16-17],而目前的粘度模型各有局限性,如双Arrhenius 模型未考虑实际反应的 级 数[11,18],Castro-Macosko 模 型 忽 略 了 凝 胶 点 附近较为明显的热效应[19-21],工程粘度模型不适用于凝 胶 速 度 慢 的 树 脂[11,19,22]等 问 题。此 外,目 前 的 浇注工艺研究多以环氧树脂为研究对象,对UPR 体系的浇注工艺研究研究较少。
为此,本研究以Fontana-Kiuna 模型为基础建立化学流变模型,得到UPR 固化时的温度-时间-粘度关系,依据工艺要求得到了浇注工艺适合的温度,并在此温度下采用有限元法模拟了UPR 包覆层的浇注过程,为UPR 包覆层的生产工艺提供参考。
1 模型建立
1.1 UPR 流变模型建立
UPR 在固化过程中存在多种化学反应,经历自由基引发、微粒凝胶、过度凝胶和大凝胶等阶段[23]。由于UPR 的粘度和固化反应相关,而固化反应又和温度相关,因此粘度本质上是热历史的函数。Fontana-Kiuna模型是由Fontana 首先提出[24]、经由Kiuna 修正[25]的一种流变模型,该模型可以在树脂的固化动力学未知的情况下,在低固化度区域预测树脂体系粘度。该模型不能精确预测某时刻的粘度,但能较好模拟整个固化过程,与工程粘度模型、双Arrhenius 模型相比,Fontana-Kiuna 模型更适合描述UPR 包覆层的流动规律[25-26]。Fontana-Kiuna 模型的基本形式为[25]:


根据α与η(T,t)的关系,使用e×η0的值求出t1,即可求出k(T),由τ=k(T) ×t可求出对应的τ值。
将α和τ代入还原,得到式(6)和式(7),整理得到UPR 流变方程为式(8),式中A,B,C均为待定系数。

1.2 包覆层几何模型建立
图1 为浇注包覆层所使用的模具,模具中流体的流域包括圆孔入口部分、底部顶部不规则部分以及药柱包覆层。模具整体高214 mm,其中药柱外层的包覆层高174 mm,厚度为1.5 mm。使用Pro/Engineer软件建立整体包覆层的几何模型,使用Hyper Mesh软件进行网格划分[28],共49916 个网格,除入口部分采用四面体网格外,其余部位均为六面体网格,几何模型如图1 所示。
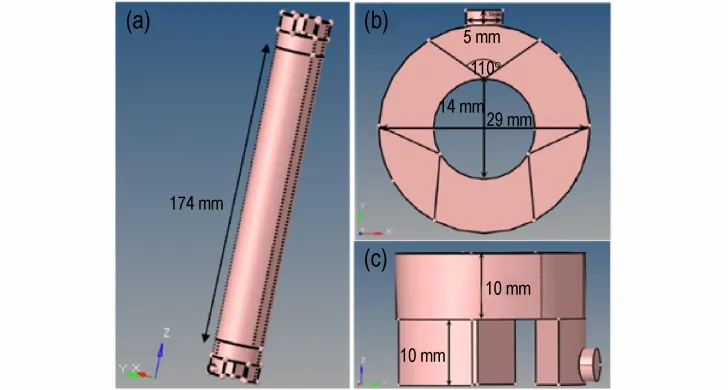
图1 模具的几何模型:(a)整体结构,(b)不规则部分XY 平面,(c)不规则部分ZY 平面Fig.1 Geometric model of mould:(a)General structure,(b)XY plane of irregular part,(c)ZY plane of irregular part
计算边界条件设置:流体入口采用体积流率设定;流体出口不受阻力,可自由流出;其余边界为壁面边界。流体浇注过程的模拟计算选用有限元瞬态体积分数VOF 模型,流体分数传输任务由系统自动生成[29]。流体入口温度为298.15 K,模具外表面设定为绝热边界。
1.3 本构方程建立
根据粘度的定义,粘度的通用格式可表示为[30]:

式中,γ为剪切速率,s-1,F(γ)和H(T)分别表示粘度的剪切速率依赖性和温度依赖性的函数。
未固化的包覆层为假塑性流体,为了拟合假塑性流体的粘度-剪切速率依赖关系,常用的模型包括幂律模 型、Herschel-Bukely 模 型、Bird-Carreau 幂 律 方 程等[27]。幂律模型仅在有限的剪切速率范围内才成立,而实际浇注中,开始时的剪切速率很大,最后趋近于零,幂律模型无法满足要求[31]。Bird-Carreau 幂律方程适用于整个充填过程中的剪切速率分析,仅考虑物理流变(剪切速率-粘度)。热固性树脂流变包含化学(时间-粘度)和物理(剪切速率-粘度)2 种流变过程,但UPR 在未固化时粘度变化很小,物理流变对粘度贡献远远大于化学流变,因此可简化为仅考虑物理流变。Bird-Carreau 幂律方程[32]可以表示为:

式中,η∞为极限剪切速率时的粘度,mPa·s;η0为零剪切速率时的粘度,mPa·s;λ为材料的时间因子;n为幂律指数。
为了拟合粘度-温度依赖关系,选用近似Arrhenius 幂律方程:

2 实验部分
原材料:不饱和聚酯(西安204 所提供),密度:1064.11 kg·m-3,导热率:0.30 W·(m·K)-1,比热容:1.60 J·(g·K)-1;环烷酸钴(北京市通广精细化工公司,钴含量7.8%~8.2%,溶剂为40%~80%的石脑油);过氧化甲乙酮(上海迈瑞尔化学技术有限公司,浓度50%,溶剂为邻苯二甲酸二辛酯);
流变性能测试:HAAKE MARS 40 应力流变仪(德国Haake 公司)。为了不破坏不饱和聚酯的固化过程,流变测试采用振荡模式,振荡频率1 Hz。取决于不同温度下的固化快慢,测量持续时间为1300~4600 s。
3 结果与讨论
3.1 粘度-温度-时间关系的研究
不饱和聚酯包覆层的配方为UPR(100 phr),过氧化环己酮(3 phr),环烷酸钴(0.3 phr),常温下混合均匀后,使用应力流变仪测试其粘度。测得的不同温度下,粘度随时间变化的曲线见图2,由图2 可知,随着时间增加,粘度增大;且温度越高,初始粘度越小,但是粘度增加更快。
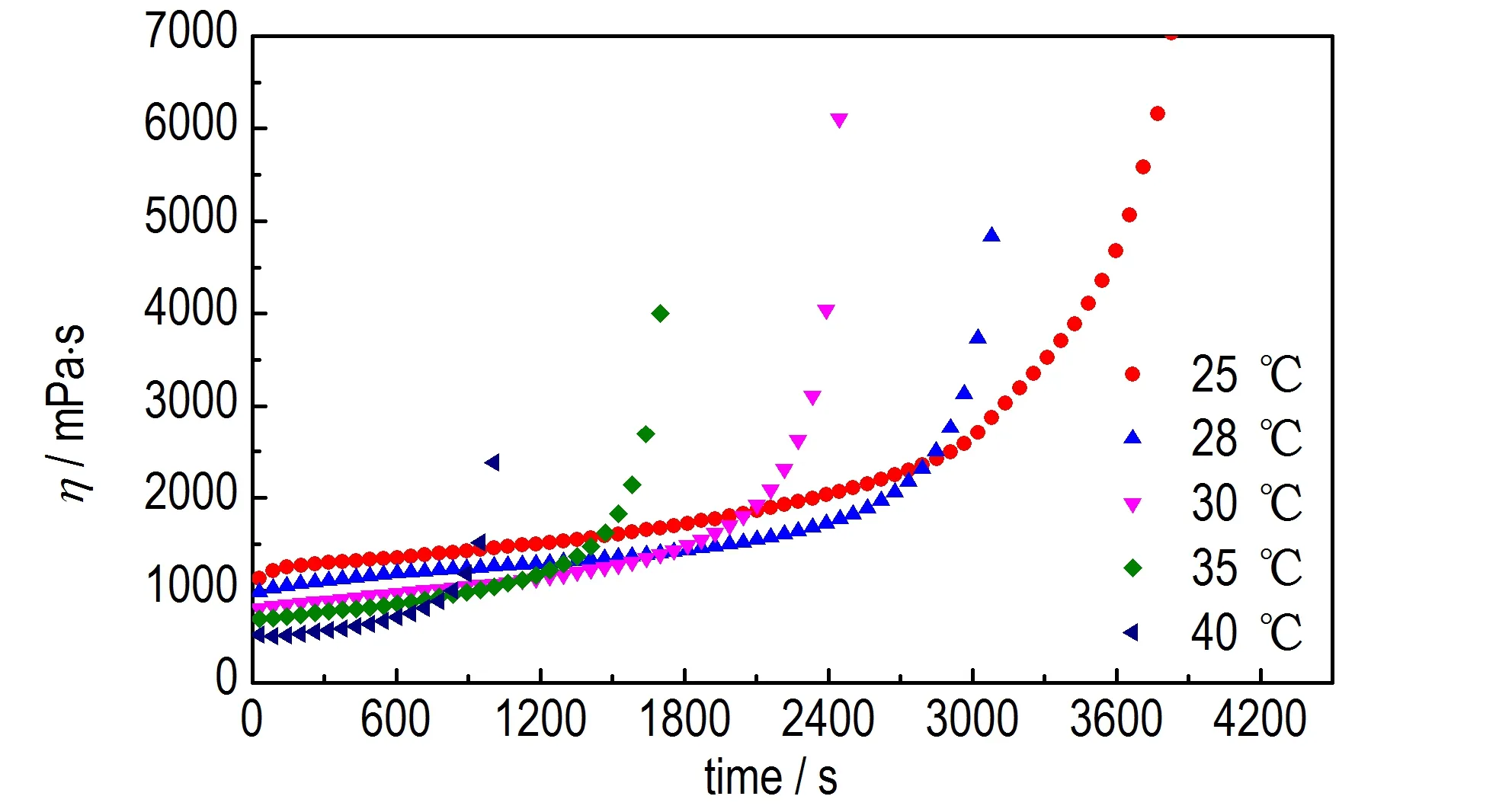
图2 在不同温度下,UPR 包覆层粘度随时间变化的曲线Fig.2 Viscosity vs. time curves of UPR coating layer at different temperatures
将不同温度下不同时间的粘度值代入式(2)~式(5),计算出相应的α和τ,绘制出α-τ的函数曲线。如图3 所示,不同温度下α-τ的曲线均呈指数曲线形式,说明在不同温度下该体系固化规律没有改变。
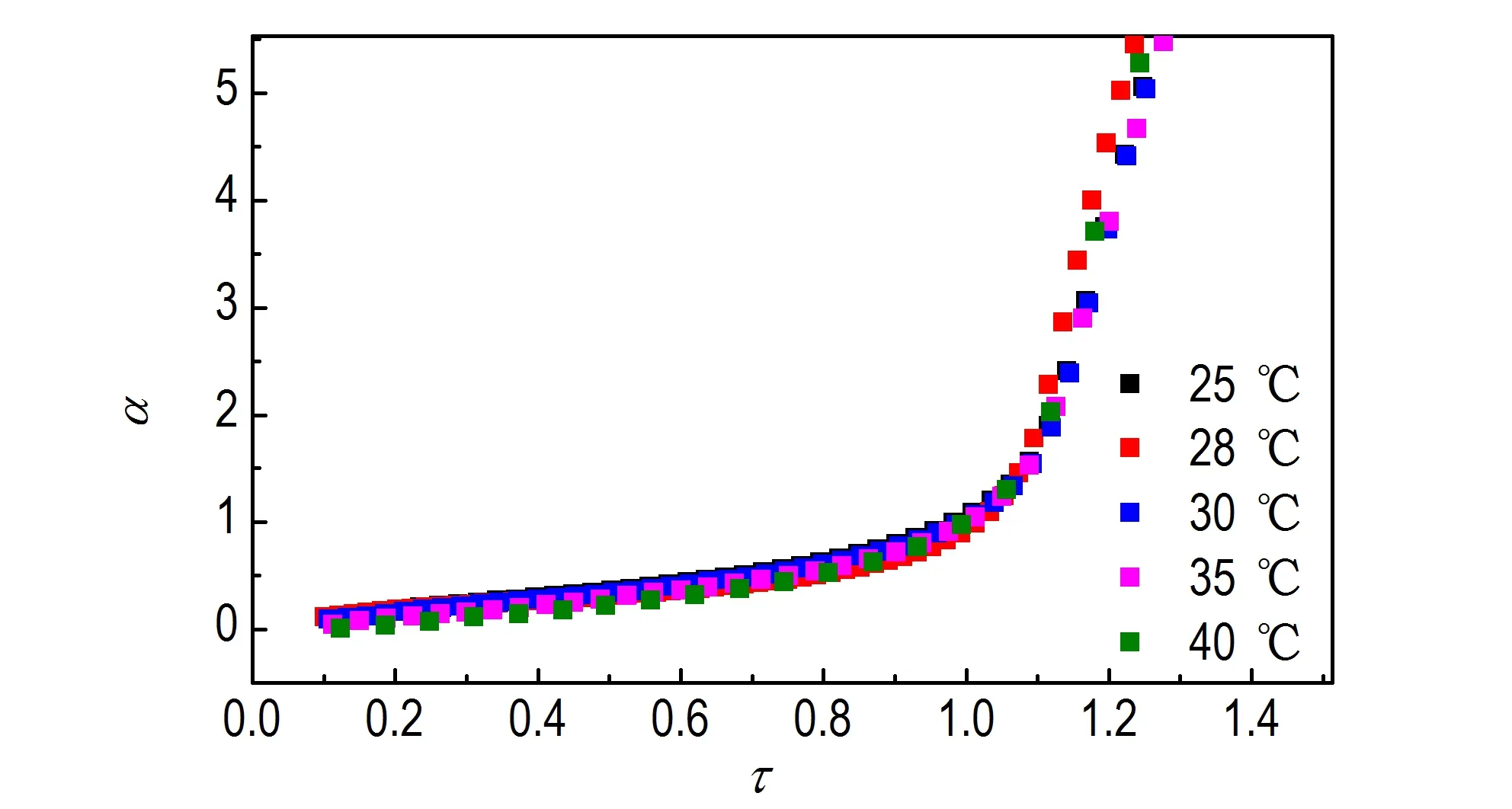
图3 不同温度下UPR 包覆层α-τ 的曲线Fig.3 α vs. τ curves of UPR coating layer at different temperatures
将式(8)输入MATLAB 软件,使用不同温度下不同时间的粘度值进行待定系数拟合,得到A,B,C 分别见表1。
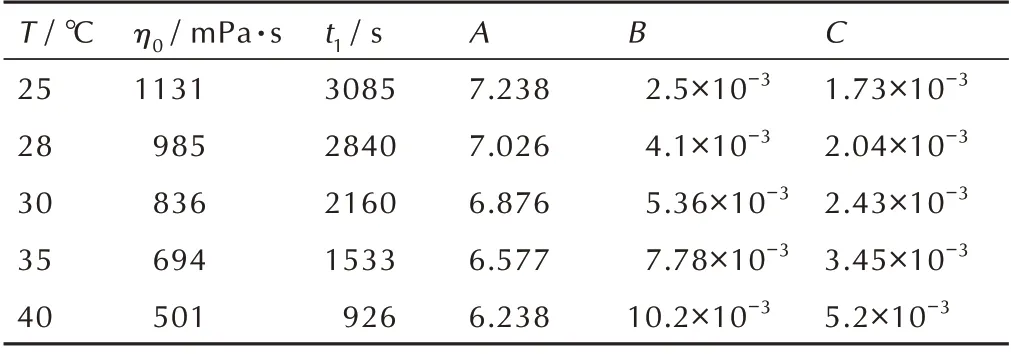
表1 不饱和聚酯包覆层体系参数表Table 1 Parameters of UPR coating layer system
再将表1 中的A、B、C代入式(8),通过Origin 进行拟合,可分别得到式(13)~式(15),即A、B、C与温度T的关系式。将A、B、C 带入式(8)得到式(16):粘度、温度和时间的关系式。不同温度下,粘度随时间变化的曲线,ln(η)-t曲线见图4,由图4 可以看出,拟合结果与实验结果吻合性较好,说明式(8)可以在25~40 ℃内拟合UPR 包覆层的流变性。
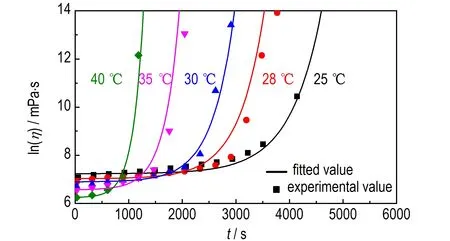
图4 不同温度下包覆层的ln(η)-t 曲线Fig.4 ln(η)vs. t curve of coating layer at different temperatures
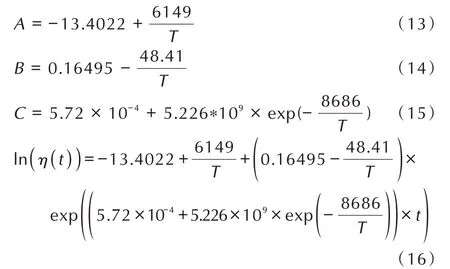
在实际生产过程中,温度会随着摩擦生热、固化反应放热等有所变化。为了得到25~40 ℃下任意温度时的粘度-时间关系,使用MATLAB 软件绘制了粘度-温度-时间三维曲线(图5),从而得到一定范围内任意温度下的UPR 包覆层粘度特性。如图5 所示,其中粘度低于1000 mPa·s 可认为是低粘度区,粘度在1000 mPa·s和3000 mPa·s之间可认为是中粘度区,粘度大于3000 mPa·s可认为是高粘度区。UPR 体系在凝胶点之前粘度变化很小,在达到凝胶点后急剧增大。随温度升高,粘度维持在1000 mPa·s 以下的时间先增大后减小,主要原因是低温下体系初始粘度较大,随着温度升高,初始粘度逐渐减小,而继续升高温度,固化反应加速造成粘度升高。根据包覆工艺要求,UPR 体系粘度低于3000 mPa·s 的时间至少为30 min,而35 ℃时,UPR 体系在低粘度区保持时间为18 min,粘度低于2000 mPa·s 的时间为30 min。因此,包覆层浇注仿真模拟时设定的温度应在35 ℃以下,以防提前凝胶化。
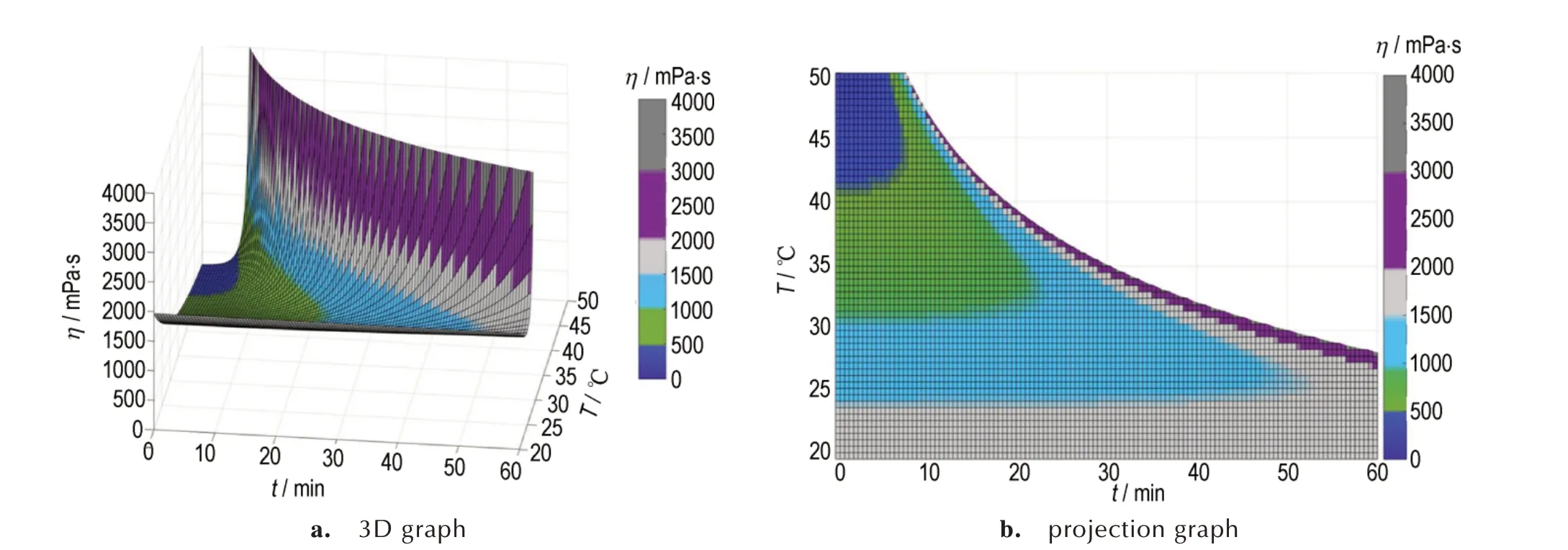
图5 UPR 包覆层温度-时间-粘度曲线Fig.5 Temperature-time-viscosity curves of UPR coating layer
3.2 包覆层浇注模拟仿真
根据本构方程(式12),使用所测得的不同温度下不同时间的粘度值进行拟合,得到:

将式(19)导入Polyflow 软件进行浇注模拟,同时假设如下:流体为不可压缩纯粘性非牛顿流体;流体与壁面之间无滑移;根据Polyflow 软件VOF 计算任务设置,计算时考虑惯性力和重力;浇注过程视为等温过程[33]。
由图5 可知,浇注模拟时的温度应在35 ℃以下,因此,选择浇注温度为室温25 ℃,在此温度下分别分析UPR 包覆层的浇注速率、浇注压力对建立的几何模型充填完整性的影响,以及UPR 充填过程的动态模拟和充填完成时熔接线的位置等。
3.2.1 浇注速率的影响
受到设备最大压力限制,浇注速率不能过快,根据经验,一般最大速率在200 mm3·s-1左右,浇注速率过慢则会降低生产效率,一般不低于50 mm3·s-1。因此,设定浇注体系温度为25 ℃,浇注速率分别恒定为50 mm3·s-1,100 mm3·s-1,150 mm3·s-1,175 mm3·s-1和200 mm3·s-1,研究不同浇注速率下的包覆层的充填完整性和整体压力分布。
1) 浇注速率对充填完整性影响
不同恒定浇注速率条件下浇注完成后包覆层的体积分数分布见图6,红色部分表示浇注完整部分,非红色部分表示浇注不完整(流体体积分数小于1)。由图6a 可见,在浇注速率为50 mm3·s-1时,顶部扇形区域的边角处有未浇注完全的地方。而图6b~6e 中流体均填满模具型腔,没有孔洞生成,因此,入口处的流率≥100 mm3·s-1才能保证充填完整。
不同浇注速率时流体浇注完成所需的时间见图6,由图6 可见,浇注速率为100 mm3·s-1时,浇注时间为400 s;增 加 速 率 到150 mm3·s-1时,浇 注 时 间 缩 短 了133.9 s,仅为266.9 s;而进一步加大速率到175 mm3·s-1,浇注时间变化不大,仅减少了37 s,再增加浇注速率,浇注时间几乎不变。考虑加工效率,浇注速率应在150 mm3·s-1以上比较合适。
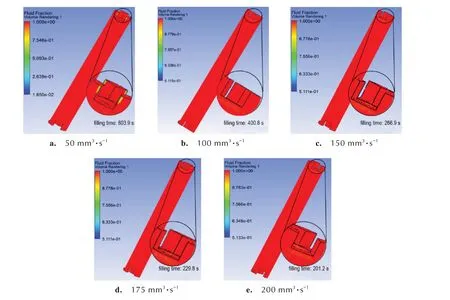
图6 不同浇注速率时的浇注时间及包覆层体积分数分布图Fig.6 Casting time and volume fraction distribution images of coating layer at different casting rates
2) 浇注速率对压力分布影响
不同浇注速率条件下形成的包覆层最大压力及压力分布见图7,包覆层底部压力较大,顶部压力较小,且随着浇注速率的增大,压力明显增加。包覆层压力的最大点位于浇注入口,当浇注速率为200 mm3·s-1时,入口处最大压力为3.52×106Pa。
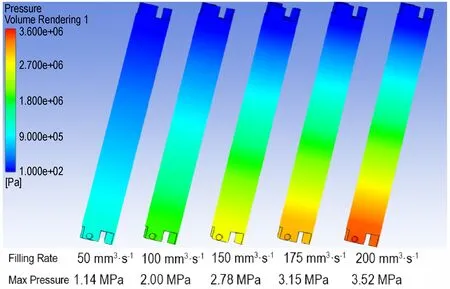
图7 不同流速时包覆层最大压力及压力分布Fig.7 The max pressure and pressure distribution of coating layer at different flow rates
不同流速下的流体流动阻力不同,因而导致入口处的压力有一定差异,且达到相同填充程度时所需的入口最大压力不同。图8 为恒定入口浇注速率时,入口最大压力与填充程度之间的关系。随着浇注速率的增加,流体流动速度变快,流动阻力相应增大,达到同样填充程度时所需的入口最大压力也随之增加。由图8 可见,在充填达到20%之前,入口处最大压力变化相对较小。填充程度在20%~80%之间时,入口处最大压力随填充程度的增加呈线性增大趋势。填充程度达到80%以后,入口处最大压力的变化相对来说也比较小。
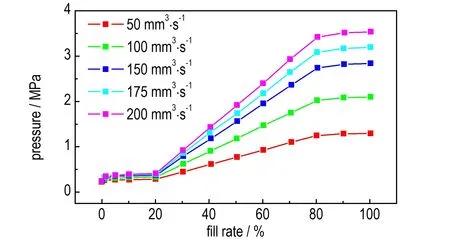
图8 不同浇注速率下入口最大压力随填充程度变化Fig.8 The Inlet maximum pressure vs. filling degree at different casting rates
在填充过程中,入口处的压力主要来源于重力和流体的粘性,因此入口处压力在填充后期比初期大很多。根据实际操作工艺的要求,设备可以提供的最大压力为3 MPa。当浇注速率为150 mm3·s-1和175 mm3·s-1时,入口处最大压力为2.78 MPa和3.15 MPa。因此,对于这种恒速浇注模式,浇注的入口流速应小于175 mm3·s-1。
3.2.2 浇注压力对充填完整性影响
设定浇注体系温度为25 ℃,浇注压力分别恒定为0.5、1、2 MPa 和3 MPa,研究浇注过程中压力对充填完整性、入口速率分布等影响。
1) 浇注压力对充填完整性影响
不同浇注压力条件下,流体填充的体积分数分布如图9 所示。浇注压力为0.5 MPa时,浇注11 min 后包覆层仍没有填充完全。浇注压力为1 MPa 时,浇注时间达到500 s 后,除顶部不规则区域的扇形区域有小部分未填充完全外,其余部分均能较好填充;当浇注压力为2 MPa 和3 MPa 时填充完全,没有空隙产生。因此,当入口处采用压力控制条件时压力应该在1 MPa以上。由图9 可见,在浇注压力为3 MPa 时,受到重力和压力的双重影响,药柱底部和顶部的压力差较大,在固化后可能引起内应力不均匀,影响药柱的性能。
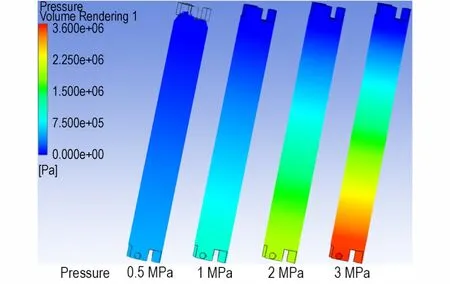
图9 不同浇注压力对体积分数分布影响Fig.9 Effect of different casting pressure on volume fraction distribution
2) 浇注压力对入口流速分布影响
图10 为恒压条件下浇注开始时,不同浇注压力条件下的入口流速分布。入口处流速呈现中心大边缘小的特点。随着浇注压力的增加,流体在入口处流速明显增大,中心位置流动速度最快。当压力为0.5 MPa时,横截面整体的流速都很低,中心的流速仅为0.001877 m·s-1;当压力达到1 MPa 时,中心区域的流速达到1.211 m·s-1,基本满足浇注的需求。浇注压力也不宜过大,若压力过大,在包覆层的同一高度上,横截面各部分速度差异大,可能引起内应力不均匀,进而导致固化后收缩不均匀,产生质量问题。
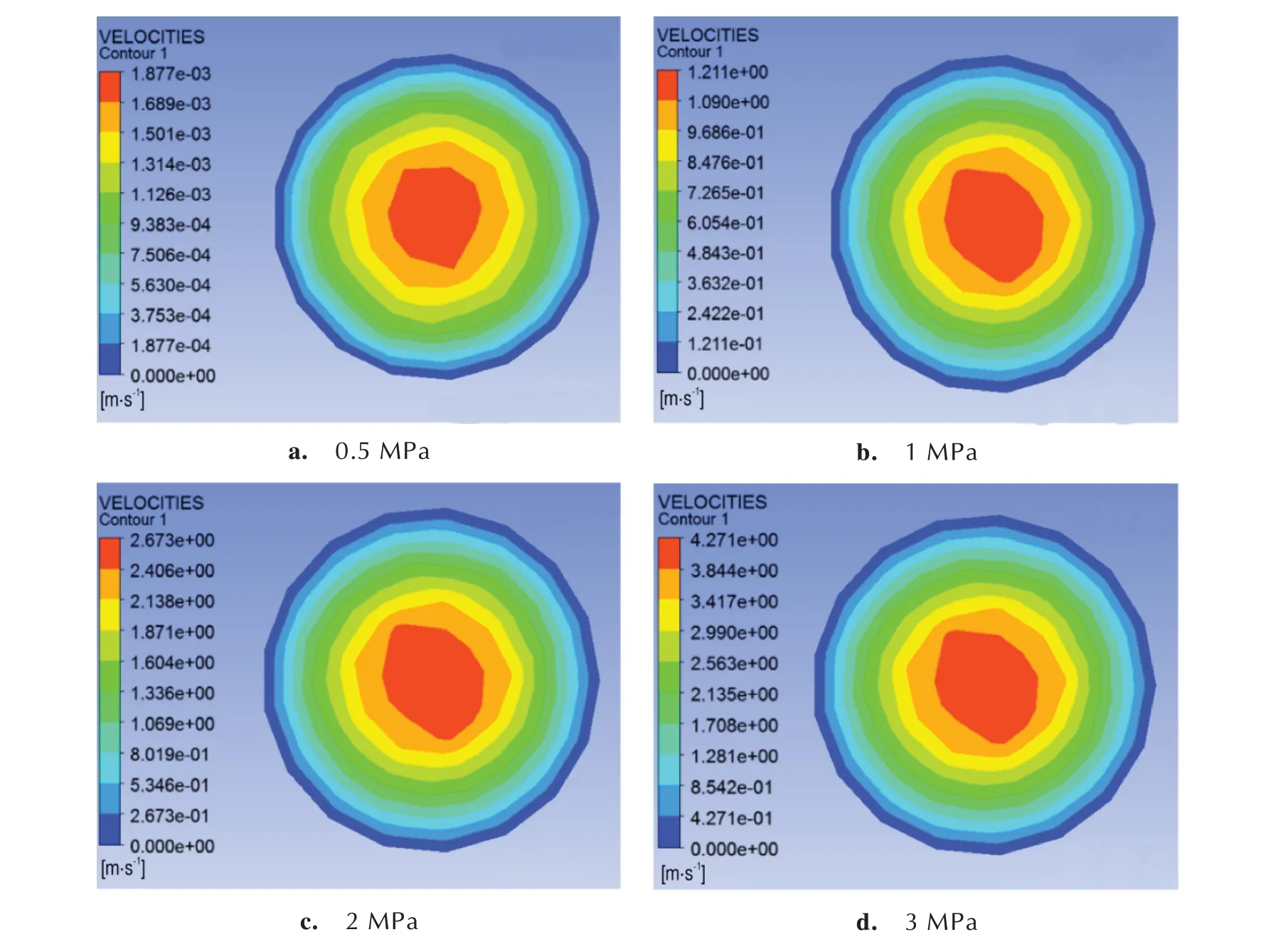
图10 不同浇注压力下初始时入口流速分布图Fig.10 The distribution images of inlet flow rate at different casting pressures
3.2.3 浇注各阶段模拟仿真
将包覆层按结构分为三部分,分别为底部流体入口部分、中间圆柱部分和顶部流体出口部分。以浇注速率为150 mm3·s-1的计算结果为例,分析流体的浇注过程。
1) 底部流体入口的浇注模拟
图11 为底部浇注过程的示意图和矢量图,矢量图根据速度方向分析流体浇注的轨迹,能够更加详细地分析流体浇注过程中的流动情况。由图11 可知,随着流体不断流入型腔,入口部分的流速最大,在浇注入口底部时,包覆层中间圆柱部分已有部分流体流入(图11a 和图11d)。在浇注底部流体入口部分时,会形成两股流体相向汇流的情况(图11b 和图11e)。流体在向另外2 个凹槽处流动时,底部还未填充满,颈部已经开始汇流,从而导致另两个凹槽底部还存在部分空隙(图11c 和图11f),由于上方流体已汇流,导致此处空气无法排出,形成缺陷。
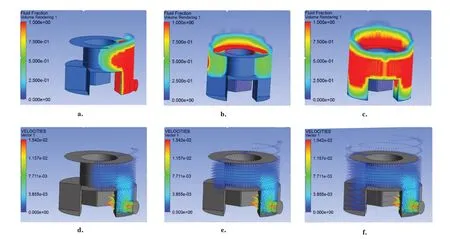
图11 包覆层底部浇注过程(a~c:示意图;d~f:矢量图)Fig.11 Casting process at the bottom of coating layer(a-c:schematic diagram;d-f:vector diagram)
2) 中间圆柱部分的浇注过程模拟
包覆层中间部分是规则的圆柱,流动过程较为简单。由图12a~12c 可知,流体刚开始浇注到中间部分时会分为两股,并在对侧融合,随后开始向上均匀浇注。由于体系粘度小,这部分会很快融合均一,再加上尺寸比较规整,所以流动较为稳定,不会出现缺陷。
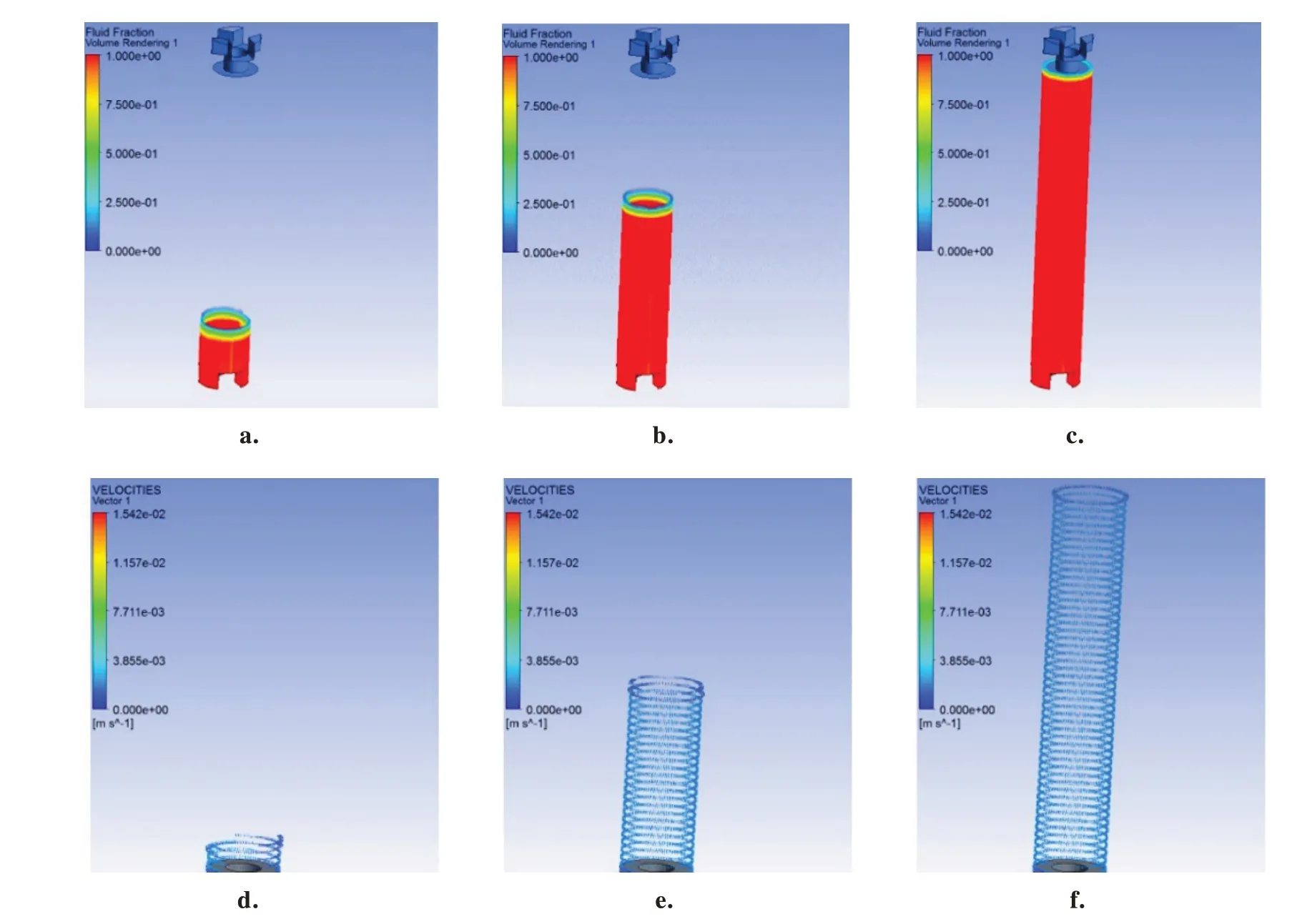
图12 包覆层中部浇注过程(a~c:示意图;d~f:矢量图)Fig. 12 Casting process at the middle of coating layer(a-c:schematic diagram;d-f:vector diagram)
3) 顶部流体出口的浇注过程模拟
流体充满中部圆柱后,继续向顶部凹槽部分流动。顶部凹槽部分的流体流动情况相对来说比较复杂,如图13所示。先从中间圆柱部位向颈部区域填充(图13a 和图13d),由于流体在中部的包覆层流动时较为平稳,没有明显的高度落差,流体的上升也呈现出整体均匀稳定的特点。在经过颈部位置后,再次继续向上流动逐渐填充凹槽顶部位置,流动状态如图13c 和图13f。
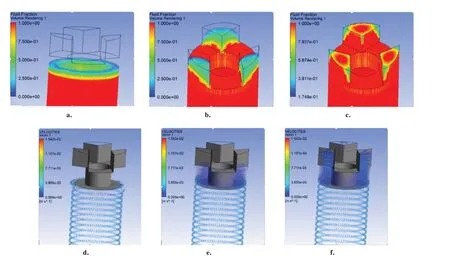
图13 包覆层顶部浇注过程(a~c:示意图;d~f:矢量图)Fig.13 Casting process at the top of coating layer(a-c:schematic diagram;d-f:vector diagram)
为了进一步观察中间薄层部分和顶部凹槽部分交界处的流动状态,每隔2 mm 建立顶部凹槽包覆层的截面。图14 为所取各截面有流体流入时的体积分数分布图,以及流体开始流入各截面对应的时间,图中194~204 mm 依次表示包覆层顶部凹槽的底面到顶面的位置。由图14 可知,流体首先填充包覆层的外围部分,之后向内侧流动,再从内侧向上流动。这种情况下就会出现多股流体融合的情况,尤其在204 mm 的顶部截面处进行填充时,包覆部分的边界处会出现明显的多股流体交融情况(图14f 中红色与橙色交接部分),这时可能会出现熔接痕。
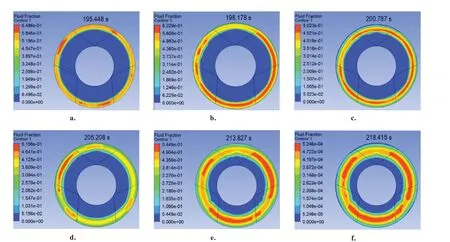
图14 包覆层顶部各截面填充体积分数分布(a~f:194、196、198、200、202、204 mm 处截面)Fig.14 Distribution of filling volume fraction of the top section of coating layer(a-f:194,196,198,200,202,and 204 mm section)
3.2.4 熔接线模拟预测
根据上面对包覆层浇注过程中的体积分数、流速、压力分布等情况的模拟分析,推测可能会出现缺陷的部位在顶部和底部凹槽部分(图15)。底部凹槽包覆部分在浇注时有两股流体相融的情况,在两股流体相汇部位有可能会出现熔接线。顶部凹槽包覆部分浇注过程中流体流动情况更复杂,会出现多股流体相融合的情况,亦有可能产生熔接线。因此,在受到外力作用时这些部位产生缺陷的可能性较大。
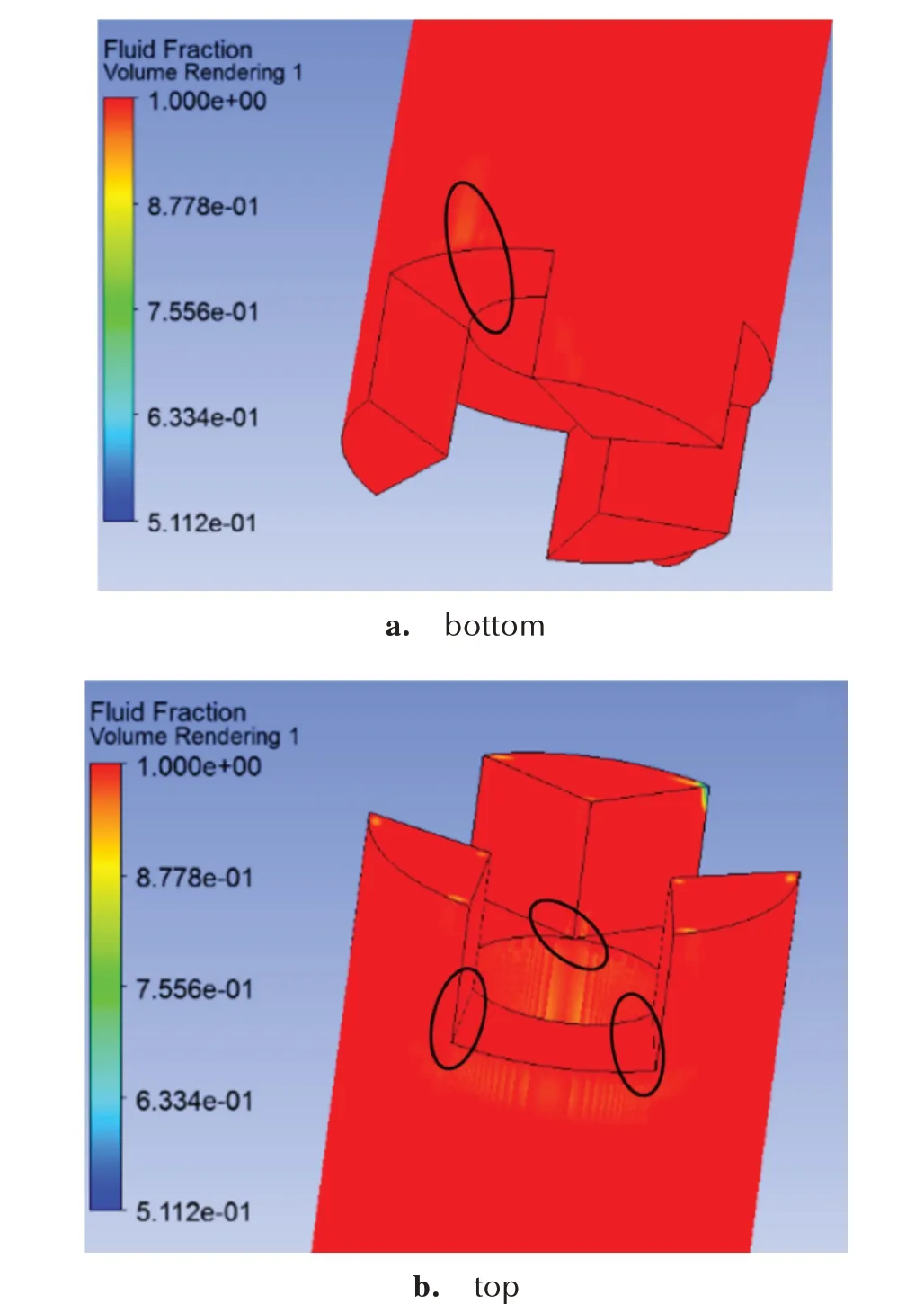
图15 包覆层的缺陷位置Fig.15 Location of defects of the coating layer
4 结论
本研究以UPR 为基体研究其浇注包覆时的生产工艺,可对包覆层连续自动化生产起到指导作用。
(1)研究了UPR 热固性包覆层的化学流变性,得到了粘度-温度-时间方程,预测了UPR 包覆层的操作工艺窗口,模型结果与实验能够很好的吻合。满足操作工艺要求时,浇注体系的最佳温度在35 ℃以下,为浇筑过程的模拟提供了合适的温度参考。
(2)通过Bird-Carreau 幂律方程建立了UPR 包覆层基体的本构方程,将其引入到Polyflow 仿真软件中模拟包覆层浇注过程中的流动规律。得到了浇注温度25 ℃时,恒定不同流率和压力模式下包覆层浇注的完整性及压力、速率分布,预测了浇筑完成时熔接线的形成位置。
(3)通过仿真模拟得到了UPR 包覆层浇注工艺参数为压力大于1 MPa,入口流速大于150 mm3·s-1且小于175 mm3·s-1。同时包覆层浇注过程中可能出现缺陷的部位在其顶部和底部凹槽部分,但可通过浇注前期降低浇注速率来避免。
