基于LightGBM的共享单车短时需求量预测

刘本兴

（太原师范学院 计算机科学与技术学院，山西 晋中 030619）

0 引 言

随着社会经济的高速发展，机动车保有量和使用频率激增，导致交通堵塞、事故频发以及空气污染等问题，而共享单车的出现有效缓解了这些问题。共享单车将公共自行车与互联网相结合，不仅在很大程度上缓解了交通压力，也为人们公共出行中的“最后一公里”提供了便捷。同时，由于共享单车具有低碳环保和使用方便等特性，受到民众的普遍欢迎。

共享单车在给人们带来便利的同时，由于存在时空需求的波动，导致区域间单车的分布量出现不平衡的问题。一方面，部分区域的单车“供过于求”，引起大量共享单车的堆积乱放，增加了共享单车平台的运营成本；另一方面，部分地区又存在“供不应求”，降低了用户的便捷度和使用率。因此，就如何在城市区域内对共享单车进行合理有效的投放，实现共享单车平稳、有序、健康、绿色、持久发展，是值得深入探讨与研究的问题。究其本质是要平衡各区域共享单车的分布量，显然，精确预测区域内共享单车短时需求量是解决问题的有效方法之一。

近年来，有关区域内共享单车需求量预测问题的研究颇多。Ma 等[1]基于微波传感数据，提出利用长短期记忆网络（Long-short Term Memory network,LSTM）模型对交通速度进行预测，在精度和稳定性方面获得比其他常用的参数化和非参数化算法更好的预测效果。XU 等[2]将LSTM 模型运用到共享单车需求量预测问题中，构建了有效预测共享单车需求量的模型。Kaltenbrunn 等[3]提出的差分整合移动平均自回归模型（Autoregressive Integrated Moving Average Model,ARIMA）通过时间序列预测方法预测站点单车的需求量，分析站点单车的状态。Singhvi 等利用线性回归模型对纽约公共自行车系统的自行车需求量问题进行了研究。宋鹏等[4]利用主成分分析法对数据降维从而降低实验的复杂度，通过构建基于不同核函数支持向量机的预测模型证明了基于径向基核函数支持向量机预测模型的有效性。曹旦旦等[5]通过天气特征数据信息分析时间因子、气象因子等对单车需求量的影响，采用长短期记忆神经网络模型准确预测共享单车的短时需求量。种颖珊等[6]根据共享单车需求量的随机性和时变性，提出一种基于随机森林和时空聚类的预测模型，该模型可以快速准确地预测出共享单车站点的需求量。刘耿耿等[7]采用时间步长为12 的双向长短期记忆的深度网络模型，该模型所预测的共享单车需求量较为精确。

在共享单车的运营方式上，国内和国外存在一定的差别，但在共享单车需求量预测问题的研究上，国外的研究对我们有着十分重要的参考意义。上述各项研究在一定程度上均实现了对某个城市或区域内整体用户共享单车需求量的预测，但是由于所考虑的相关因素不足，建模所选择的特征向量也比较理想化，对于无特定周期且波动明显的数据，仅仅使用时序模型是远远不能达到精度要求的，因此需要采用更加有效的方法实现更加精准的预测。

针对目前共享单车分布及调度所存在的问题，本文将天气因素对共享单车需求量的影响考虑在内，采用轻量级梯度提升机（Light Gradient Boosting Machine,LightGBM）算法[8-10]构建模型，由于算法运行速度快且所占内存小，能够减少模型的训练时间。通过贝叶斯超参数算法对LightGBM 的参数进行优化，可以实现对共享单车短时需求量的预测，达到更快的训练速度以及更好的预测性能。

1 需求影响因素分析

1.1 数据概况

本文采用如表1所示的UCI 机器学习库中的数据集Bike Sharing Data Set。该数据集提供跨越两年并以小时为单位进行统计的共享单车短时租赁数据，同时考虑了天气、季节、时间等特征因素对共享单车使用量的影响。

表1 原始数据信息

1.2 数据分析

按照时间顺序刻画整个数据集中共享单车的需求量，如图1所示。

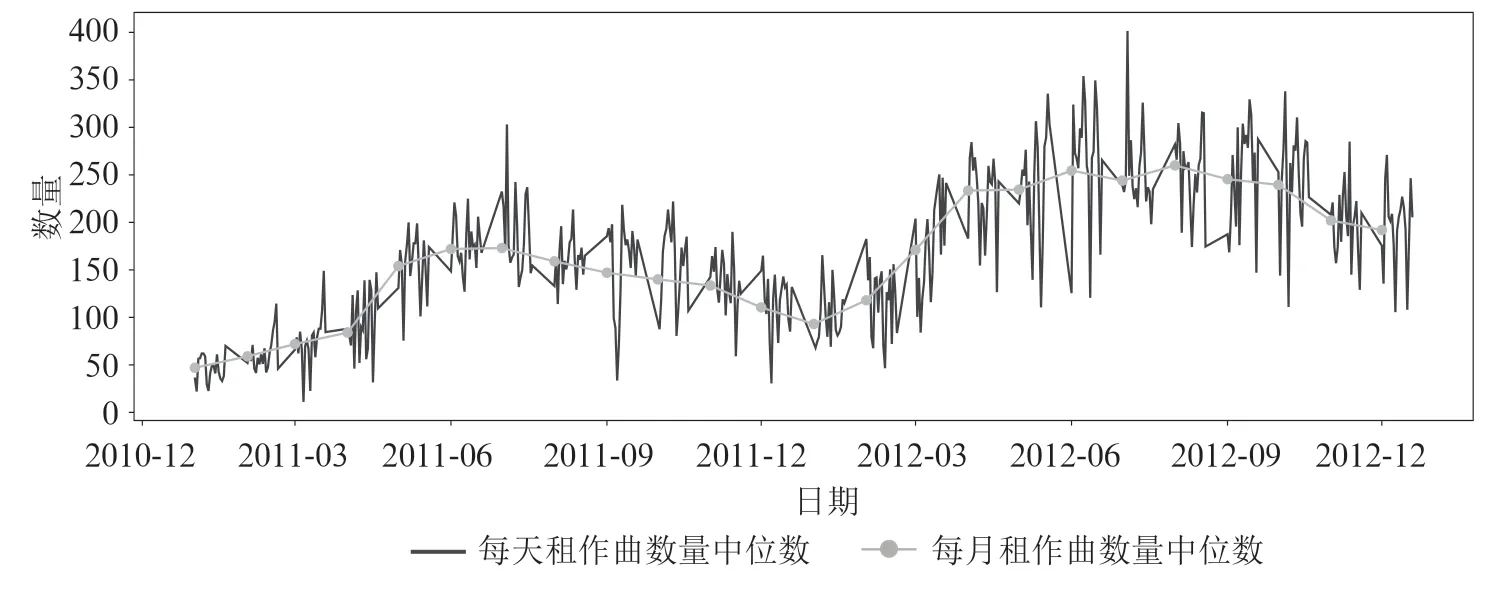
图1 共享单车需求量

由图1可知，2012年共享单车的需求量相较于2011年有所增加，且波动幅度具有周期性、逐月、逐年递增变化。根据这种变化特点，可以从由日期和时间构成的数据datetime 中提取出年、月、日、小时和星期几，然后去除日期。对于特征holiday，数值为0 表示非节假日，数值为1 表示节假日；对于特征workingday，数值为0 表示非工作日，数值为1 表示工作日。对于特征天气，数值1、2、3、4 分别代表晴天、阴天、小雨或小雪、恶劣天气。实际温度、体感温度单位为摄氏度。

将处理后的数据，基于数据类型中的浮点型因素和枚举型因素对共享单车借车数的影响进行分析。

1.3 浮点型因素特征分析

根据数据集中不同实际温度、体感温度、湿度、风速下的每小时共享单车借车数量绘出散点图，从而分析出不同特征因素对租赁量的影响，如图2所示。

由图2（a）和（b）可知，数据点主要集中于温度的某个范围内，说明共享单车租赁量在某个温度范围内比较高，而温度太低或者太高，共享单车租赁量则会明显降低。且由图2（a）和（b）可知，实际温度和体感温度的散点图走向是一致的，说明实际温度和体感温度对共享单车租赁量的影响基本相同，其中一个特征因素就能反映对共享单车租赁量的影响。从图2（c）中可以看出，在一定的湿度范围内，单车的租赁量没有明显的变化。由图2（d）可知，当风速逐渐增大时，单车的租赁量越来越少，说明风速对共享单车的租赁量有很大的影响。

图2 不同特征因素与单车租赁量关系散点图

1.4 枚举型因素特征分析

时间、季节、节假日、天气为离散特征，可以采用统计的方式分析是否具有相关性。根据数据集中时间、月份、季节、天气影响因素绘制每小时的共享单车借车数量，如图3所示。

由图3（a）可知，4月—10月共享单车租赁数量较多；图3（b）中显示共享单车租赁数量在夏季和秋季时最多；由图3（a）和（b）可以得出结论，月份和季节对共享单车租借数量的影响大致相同，但是月份信息更加全面，因此留下月份特征，删除季节特征；从图3（c）中可以看出，工作日租赁数量比非工作日多，且天气晴朗时租赁量明显高于其他天气状况下的租赁量，说明天气状况与共享单车租赁量有很大的相关性；从图3（d）中可以看出，工作日存在早晚高峰期，早高峰在7:00—8:00 点左右，晚高峰在17:00—18:00 点左右。此外，11:00—14:00 点的使用量较高；节假日共享单车使用量较高的时间段为9:00—19:00。由此可知，共享单车需求量在不同时间段（尤其是早晚高峰时段）差异较大。

图3 不同月份、季节、天气、小时共享单车使用量

2 基于贝叶斯优化的LightGBM 共享单车短时需求量预测模型

2.1 LightGBM 算法介绍

2.1.1 算法原理

LightGBM 是梯度提升决策树（Gradient Boosting Decision Tree,GBDT）的一种高效实现。它的原理与GBDT 相似，将当前决策树残差的近似值替换为损失函数下降最快的方向即负梯度以此来拟合新的决策树，即每一次迭代都在原来模型不变的基础上，通过新增一个函数到模型中，使预测值不断逼近真实值。它的独特性包括以下几点：一是基于梯度的单面采样决策树（Goss），二是排他特征绑定（EFB）算法，三是基于深度限制的直方图，四是叶片生长策略。

训练目标函数如式（1）所示，其中yi为标签的真实值，为第K-1次学习的结果，为前K-1 棵树的正则化项和，目标函数的含义为寻找一棵合适的树fk，使得函数的值最小：

泰勒公式对目标函数进行展开，可得：

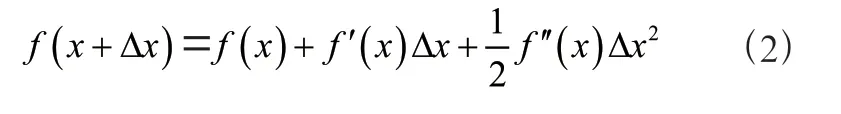
损失函数的二阶泰勒展开结果为：

用gi记为第i个样本损失函数的一阶导数，hi记为第i个样本损失函数的二阶导数：

简化后的目标函数可表示为：

2.1.2 算法优势

直方图算法通过离散化的方法将连续的浮点数转化为K个整数，同时生成一个直方图，宽度为K。遍历数据的时候，在直方图中，先统计累积索引离散化后的特征值，然后遍历图中离散值索引对应的特征值，依次计算以获得最优分割点。由此可以大大减少内存的占用，不仅节约训练时间，同时也削弱了噪声带来的影响，从而提升了精度，如图4所示。

图4 直方图算法原理

LightGBM 在直方图算法的基础上，不再采用传统的Level-wise 策略，而是通过一种更为高效的带有深度限制的leaf-wise tree growth 策略。leaf-wise 策略是通过循环遍历所有叶子节点，并依次计算每个叶子的分裂增益，对每次循环中增益最大的叶子进行分裂。此方法与Level-wise 相比，当分裂次数相同时，leaf-wise 不仅误差较小，而且精度更高。同时LightGBM 在保证高效率的前提下为了防止出现模型过拟合现象，在树生长过程中增加了最大深度限制，如图5所示。

图5 Leaf-wise tree growth 策略

2.2 贝叶斯超参数优化算法

贝叶斯超参数优化算法的基本思想是根据过去目标的评估结果建立代替函数，以此找到目标函数的最小值。在此过程中，所建立的替代函数比原始目标函数更容易优化，并通过proxfunction 应用特定标准来选择要评估的输入值。贝叶斯调参的迭代次数少，运行速度快，还可以实现多个参数同时调整，不仅降低了维度爆炸的可能性，而且还缩短了运行时间。贝叶斯超参数优化算法只制定参数大体的变化范围，不考虑如何进一步细分范围。

根据数据集的数量和划分，设定调参范围，并同时对最大叶子数、最大深度、学习率、最小分裂增益样本抽样率和特征抽样率等多个参数进行调参，最终结果如表2所示。

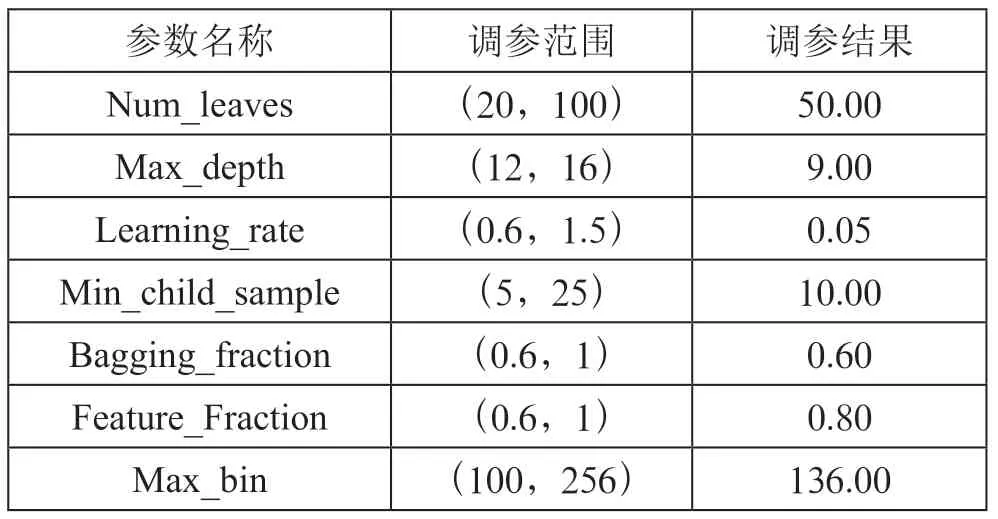
表2 贝叶斯优化的调参范围与结果

2.3 共享单车短时需求量预测模型构建流程

基于贝叶斯优化的LightGBM 算法共享单车短时需求量预测模型构建由以下几个部分组成。首先，对所采用的数据集进行预处理，主要包括缺失值处理，数据格式转换等；其次，对影响共享单车使用量的特征因素进行分析和特征选择，最终数据集包含7 个特征因素；接着将整个数据集划分为训练集与测试集，通过贝叶斯优化算法优化超参数；最后，采用测试集对优化后的模型进行测试，通过测试结果评估模型性能，进而获得最终模型。其中，训练集和测试集按8:2 的比例划分，共享单车的租赁量作为决策属性，将特征选择获得的7 个属性作为特征属性，算法预测流程图如图6所示。

图6 共享单车短时需求量预测模型流程图

3 实验结果与分析

3.1 数据描述

研究所使用的数据中包含12 个属性和10 886 个观察值，提供了跨越两年的每小时租赁数据，包含天气信息和日期信息，训练集由每月前19 天的数据组成，测试集由每月后10天的数据组成。本实验的数据是通过统计由以小时为单位的数据组成，其中数据的每一行代表一天中的某一特定时间。本文使用Python 中的sklearn 工具包来构建预测模型，调整模型参数后，利用LightGBM 模型进行预测。

3.2 数据归一化与反归一化

由于数据特征因素之间的基本度量单位不同，导致特征因素对共享单车借车量的结果分析产生较大的影响，从而掩盖了实际情况，因此通过离差标准化对数据进行归一化处理以统一各属性量级，转换方法如下：

通过反归一化还原预测结果为原本的量纲，方便后续的结果分析，计算公式为：

其中，xi表示原始数据，表示归一化之后的无量纲数据，y表示反归一化后的数据。

3.3 评估指标

回归模型的评估指标用来衡量预测值与真实值之间的偏差，采用数据集中的实际数据来评估模型的预测精度。本文采用均方根误差（RMSE）、绝对误差的平均值（MAE）和平方相关系数（R2）对模型的可靠性进行评估，其计算公式分别为：

3.4 预测结果对比分析

利用评估指标MAE、R2和RMSE 检验模型的性能，并对预测结果进行误差分析。利用贝叶斯优化后的LightGBM模型预测12月15日每小时的用户共享单车借车数量，结果如图7所示。

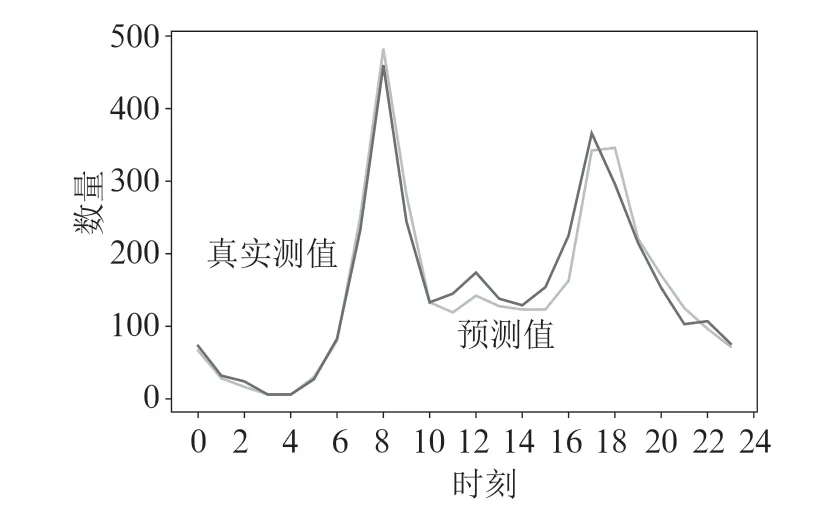
图7 贝叶斯优化后的LightGBM 模型预测结果

由图7可以看出，采用气温、风速、天气、小时、月份、工作日与否、节假日与否作为影响因素，能更加准确地预测区域内用户每小时的共享单车借车需求量。其中，绿色线为预测值，红色线为真实值，对比预测值与真实值，两者接近并且变化态势一致。

为证明本文所构建模型的可靠性和准确性，将该模型与基于XGBoost 的预测模型和基于随机森林的短时需求预测模型的预测结果进行对比，评价指标结果如表3所示。

表3 三种模型的评价指标平均值对比表

由图7和表3可知，比较三个指标的评估结果，经过贝叶斯优化的LightGBM 算法的预测效果优于其他算法。

基于贝叶斯优化的LightGBM 模型的MAE 的最小值为0.494，低于XGBoost 模型和随机森林模型，说明其预测结果更准确，且该模型的RMSE 也低于XGBoost 模型和随机森林模型，说明该模型的预测结果更可靠。此外，本文模型的R2高于另外两个模型，说明该模型的拟合效果优于其他两个模型。

综上所述，经过贝叶斯优化的LightGBM 模型可以更加精确地预测区域内共享单车的短时需求量，与XGBoost 模型和随机森林模型的预测结果相比，该模型的预测精度更高，预测结果更可靠。

4 结 论

共享单车的出现满足了人们日常短途出行的需要，缓解了城市交通拥堵和环境污染问题。与此同时，共享单车投放量不平衡问题也会导致社会资源的浪费和民众使用便捷性的降低。因此，对共享单车的需求量进行准确的预测，这一举措对共享单车的合理分布与科学调度是十分重要的。本文提出的基于贝叶斯优化的LightBGM 算法，在共享单车短时借车需求量的预测上为相关人员提供了更有效、更准确的方法，可以为共享单车特定区域的投放量测定，以及区域间共享单车的调度提供指导依据，有助于实现共享单车供给与用户需求的适度匹配。实验结果表明，本文所提出的模型对共享单车短时需求量的预测性能最佳，但是对于一些波动比较大的数据则无法准确预测，为此我们不会止步于前，而是进一步开展相关研究。