数学史渗透数学教学的微思考
——以“有理数”单元为例
2022-11-17黄贤明江苏省苏州高新区景山实验初级中学校215129
黄贤明 (江苏省苏州高新区景山实验初级中学校 215129)
近年来,数学史与数学教育(HPM)的研究在国内受到广泛关注,并从理论与实践上证实了HPM的教育价值.正如“使面包和黄油更加可口的蜂蜜”,数学史使数学学习更具有吸引力.对学生而言,数学史既能促进他们对数学知识的理解,拓展相关的数学背景,还可以引发学习数学的共鸣,培养正确的价值观.对教师而言,数学史能帮助预测学生在数学学习中的困难,进而指导教学,同时丰富了教学资源,提升课堂的文化底蕴[1].本文介绍了“有理数”单元中数学概念的历史,并分析了不同版本教材中“有理数”单元的数学史,提出在“有理数”单元渗透数学史的思考与建议,敬请指正.
1 “有理数”单元中的数学概念的历史
通过介绍“有理数”单元中负数、有理数和乘方的历史,让学生发现中国古代对于有理数及其运算的发展作出了巨大的贡献,相比同时期的国外处于相对领先的地步.
1.1 负数的历史
负数的历史源远流长,它的概念最早出现在《九章算术》中,书中的“方程”章主要讲解了“方程术”,在方程组的加减消元中就出现了负数的情形.为处理该情形,书中给出了正负数运算法则——“正负术”.同时,书中也给出了许多正负数的例子,如“方程”章中将“卖”记为正、“买”记为负,“余钱”记为正、“不足钱”记为负.数学家刘徽对正负数给出“今两算得失相反,要令正负以名之”的定义,更明确了正负数是用于表示相反意义的量,并用红色(正放)算筹表示正、黑色(斜放)算筹表示负.
在国外,对负数的认识比中国要晚很多.欧洲数学家更多关注负数的合理性,他们认为0是最小的数,而比0小的数是不存在的,即负数是荒谬的.直到19世纪整数理论基础建立,负数才逐渐被普遍认可.
1.2 有理数的历史

1.3 有理数乘方的历史
刘徽在《九章算术》中用“幂”表示矩形的面积,这是在数学著作中首次出现的“幂”.此后在《数书九章》《四元玉鉴》等数学文献中,“幂”均表示一数的平方.1607年,徐光启在《几何原本》的译本中重新使用“幂”字,并将其定义为“自乘之数”,这就相当于定义“幂”为an.指数的概念最早出现在我国古代的音乐理论中.《管子》中说:“先主一而三之,四开合九九.”其中“四开”表示连乘4次,这将指数的概念明显地表达了出来,也就是1用3去乘,连乘4次,得到结果就是九九之数,即34=9×9=81[3].
在西方,乘方运算起源很早,但指数的概念形成较晚.在法国数学家韦达用字母表示数之后,相关幂的记法层出不穷,直到法国数学家笛卡尔创造了幂的新记号an,瑞士数学家欧拉补充给出了指数的概念,自此形成了教材中乘方、指数等概念的定义与幂的符号[4].
2 不同教材中“有理数”单元的数学史
教材是教学内容的重要载体,是教师教学的主要依据,教材中的数学史内容是教师进行HPM教学的首要参考.现行的许多教材都通过设置特定栏目、选择数学史习题等方式呈现数学史,供学生课后阅读拓展.数学史在数学教材中的呈现方式主要有:点缀式、附加式、复制式、顺应式和重构式[5](表1).“有理数”单元中蕴含着丰富的数学史料,以国内人民教育出版社、江苏凤凰科学技术出版社、北京师范大学出版社和华东师范大学出版社(以下分别简称为人教版、苏科版、北师大版、华师大版)的四本七年级上册数学教材为例,分析不同教材中“有理数”单元的数学史(表2).
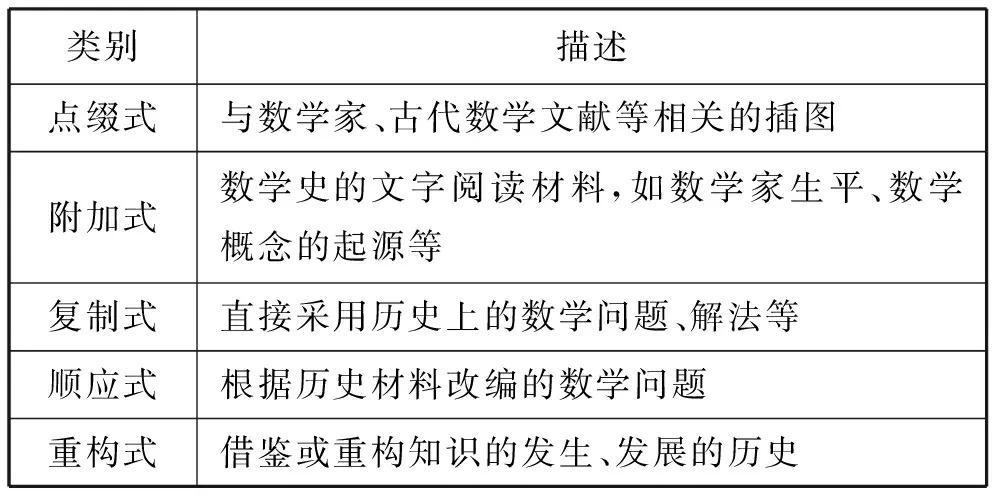
表1 数学教材中数学史的呈现方式

表2 不同版本教材“有理数”单元中的数学史
(1)编排数学史的章节.在四本教材中,数学史的呈现主要集中在有理数、有理数的运算和有理数的乘方这三个章节中.编排数学史的章节与“有理数”单元中数学概念历史基本吻合.
(2)渗透数学史的内容.在四本教材中,“有理数”单元数学史的内容主要为数的发展、负数的历史、棋盘摆米的故事和幻方.其中负数的历史在四本教材中都专门设置了阅读板块呈现.在人教版和华师大版中主要围绕《九章算术》讲述了中国负数的历史,并重点介绍了“正负术”.人教版给出了用红黑算筹进行有理数加减运算的图示,直观地呈现了古代的运算方式,吸引力与可读性更强;华师大版的材料中详细介绍了《九章算术》和“正负术”,篇幅较大,且材料中出现“加减消元法”“韦达”等名词,超越了学生的认知水平,难以引发学生的阅读兴趣和认知共鸣.苏科版和北师大版都从国内外两个方面介绍了负数的发展.苏科版是史料的列举,学生浅尝辄止,只能体会到负数发展的漫长;北师大版从中国负数概念的历史切入,并与国外负数概念建立的曲折对比,选取内容更利于学生形成对负数的文化性理解.
(3)数学史的呈现方式.在四本教材中,“有理数”单元的数学史呈现方式以附加式为主,顺应式等其他方式为辅.附加式的内容均在课后阅读栏目中呈现,作为学生课后补充阅读的相关素材.顺应式的数学史只聚焦于中国传统游戏幻方.其他方式在四本教材的“有理数”单元中基本没有体现.
3 思考与建议
3.1 有“米”而炊:融合不同版本教材
在HPM教学中,教师最大的烦恼就是缺乏数学史素材,而不同版本的教材就会从多种角度为教师提供数学史料.例如,在“正数与负数”一课中,教师可选取人教版“数的产生与发展”的图片引入,揭示数的产生与发展离不开人类社会发展的需要,并提出“数0就表示‘没有’吗?”的问题,以数学史上西方对数0的困扰来导入对负数的探索,重构负数的历史;在课后拓展环节,可选取北师大版的阅读材料“负数小史”来介绍中外负数的历史,促进学生文化性理解的形成,增强民族自豪感.教师在教学中有选择地将不同教材中的史料融合,发挥它们的优势与亮点,同时将数学史素材“问题化”[6],引导学生重走数学内容的产生与发展过程,形成对数学史的内在认同,真正发挥出数学史的育人价值.
3.2 多样呈现:让课堂浸润数学史
就数学史在教材中的呈现方式而言,附加式偏多,其他方式相对较少.在实际教学中,教师应弥补教材的不足,以多样化的方式呈现数学史,增添课堂的文化味.以苏科版教材为例,在“有理数”单元,教材更关注有理数内容的生活化,淡化了有理数中蕴含的历史价值.此时,教师可以在教学课件中以点缀式或附加式呈现相关史料,如《九章算术》中的“正负术”简介、数学家刘徽的图片、《九章算术》书影,等等.其次,可有目的地选取合适的课题组织重构知识发生的历史.另外,教师也可设计数学史主题的导学案,将精选的史料以纸质形式呈现给学生,以此增强学生学习数学的兴趣.
3.3 指向理解:数学史为知识学习服务
数学史料的选取要具备趣味性、科学性、可学性、有效性和人文性[7].这些数学史的选取以及在课堂教学中渗透的目的不仅是为了学生情感与价值观的培养,更重要的是为学生理解数学知识、领会数学思想和掌握数学方法,做到数学史为数学学习而服务.例如,在有理数概念的教学中,教师可呈现有理数名称由来的数学史料,但其目的是建立“理”与“比例”之间的联系,消除学生从字面意思来理解有理数而产生的困惑,促进学生对有理数概念的理解.
总之,数学史并非教师的“作秀”工具,数学史的渗透有其深层次的价值与意义.作为一线的教育工作者,更要重视教材、教学内容背后的数学史,真正让数学史落实到课堂中,真正让数学史从“史学形态”走向“教育形态”[8].
