基于改进粒子群算法的配电网无功优化研究
2022-11-16张尚然
张尚然
(河北石油职业技术大学 电气与电子系,河北 承德 067000)
随着工业的发展和人民生活水平的提高,我国的用电需求不断提升,配电网的规模也随之不断加大,配电网中的网络损耗所带来的电能损失巨大,为了维持高质量供电的同时减小配电网的电能损失,需要对配电网络进行无功优化。常用的无功优化方法包括线性规划法、非线性规划法、混合整数规划法及动态规划法等,其都存在着计算量较大、收敛性差和稳定性差等缺点[1-2]。粒子群算法具有参数设置不多、收敛速度快等优点,本文采用改进粒子群算法对配电网络进行无功优化,通过MATLAB软件进行仿真建模,达到降低网损的目的。
1 配电网无功优化模型
首先建立配电网无功优化模型,将有功网损作为目标函数,引入节点电压越界罚函数和动态权值系数来处理状态变量,得到最终的目标函数为:
(1)
其中:Ploss表示有功损耗;n表示配电网系统中的负荷节点数。
节点的有功功率、无功功率等式约束方程为:
(2)
其中:i∈n,n代表系统节点数量;PGi、QGi是在节点i处注入的有功功率和无功功率;PLi、QLi是节点i处所带负荷的有功功率和无功功率;QCi是节点i处的无功补偿量大小;Gij和Bij分别代表电导和电纳;δij是相角差。
除上述等式约束方程外,控制变量的约束条件为:
(3)
其中:VGi代表发电机端电压;PDGi和QDGi是分布式电源的有功和无功功率。
状态变量的约束条件是:
(4)
其中:QGi是发电机的无功;VDi.max和VDi.min是节点i处电压的上、下限。
2 改进粒子群算法
2.1 基本PSO
粒子群算法(Particle swarm optimization简称PSO)的主要思想是模拟种群的社会活动,种群的个体间信息是交叉传递的,所有个体都拥有学习能力,从而使种群的进化更加迅速[3]。假设存在d维空间,在这个d维空间内,将第i个粒子的位置和速度分别表示为:
Xi=(xi1,xi2,…,xiD),i=1,2,…,N
(5)
Vi=(vi1,vi2,…,viD),i=1,2,…,N
(6)
迭代运算中,粒子通过优化目标函数得出适应度函数,对粒子群进行适应度求解,找到种群中适应度最高的两个粒子,对两个最优粒子进行更新。
得到的最优位置为:
Pbest=(pi1,pi2,…,piD),i=1,2,…,N
(7)
得到的全局最优位置表示为:
Gbest=(g1,g2,…,gD)
(8)
得出两个最优值后,对粒子进行速度与位置的迭代:
Vij(t+1)=ωvij(t)+c1r1[pij-xij(t)]+c2r2[pgj-xij(t)]
(9)
Xij(t+1)=xij(t)+vij(t+1),j=1,2,3…d
(10)
其中:ω是惯性系数,c1、c2是学习因子,r1、r2是均匀分布在0至1间的随机数。
2.2 线性递减惯性权重PSO
在基本PSO内,ω是固定的数值,当ω较大时,PSO能够更加轻易的找到局部最优解,更快的搜索到全局变量;当ω较小时,能够在当前区域位置搜索的更精确,收敛速度更快,所以当ω是固定数值时,其数值的大与小各有优势[4]。
在改进PSO时,引入线性递减惯性权重,将ω设置为线性变化的函数,使惯性权重从最大值线性减小至最小值,ω不断随着算法的迭代进行改变,公式如下:
(11)
其中:ωmax代表ω的最大值,ωmain代表ω的最小值,t代表算法此刻的迭代数,tmax代表最大迭代数,在运算中一般设ωmax=0.9,ωmin=0.4。
3 算例分析
下面给出一个IEEE14节点系统[5],以此作为算例进行分析。
PSO无功优化的参数设置如下:设粒子种群是40,迭代次数是100,学习因子c1=c2=2,其中基本PSO的惯性系数为固定大小ω=0.8,改进的PSO的线性递减惯性权重ωmax=0.9,ωmin=0.4,惩罚系数λ1=1,λ2=2。
3.1 样本参数(见表1,表2,表3,表4)
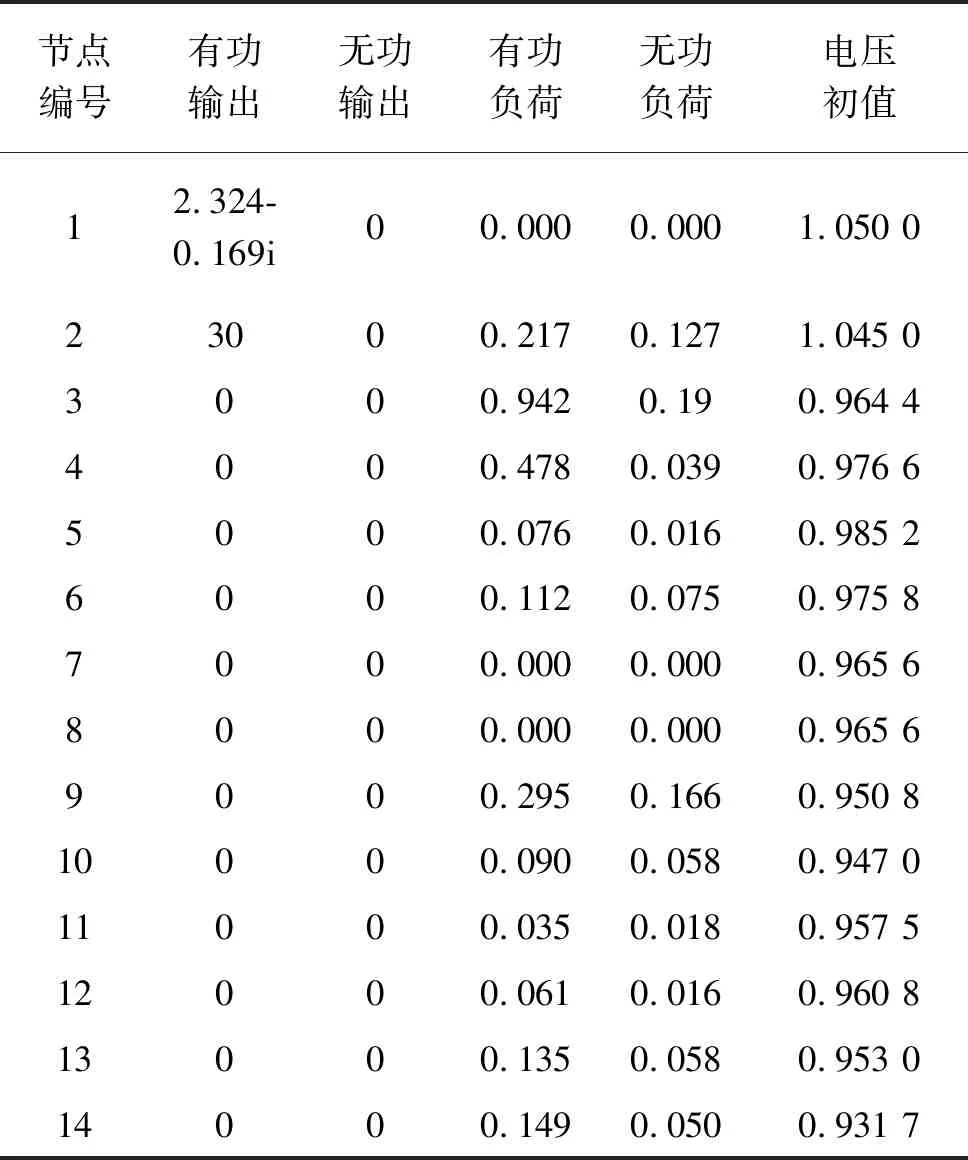
表1 IEEE14节点数据
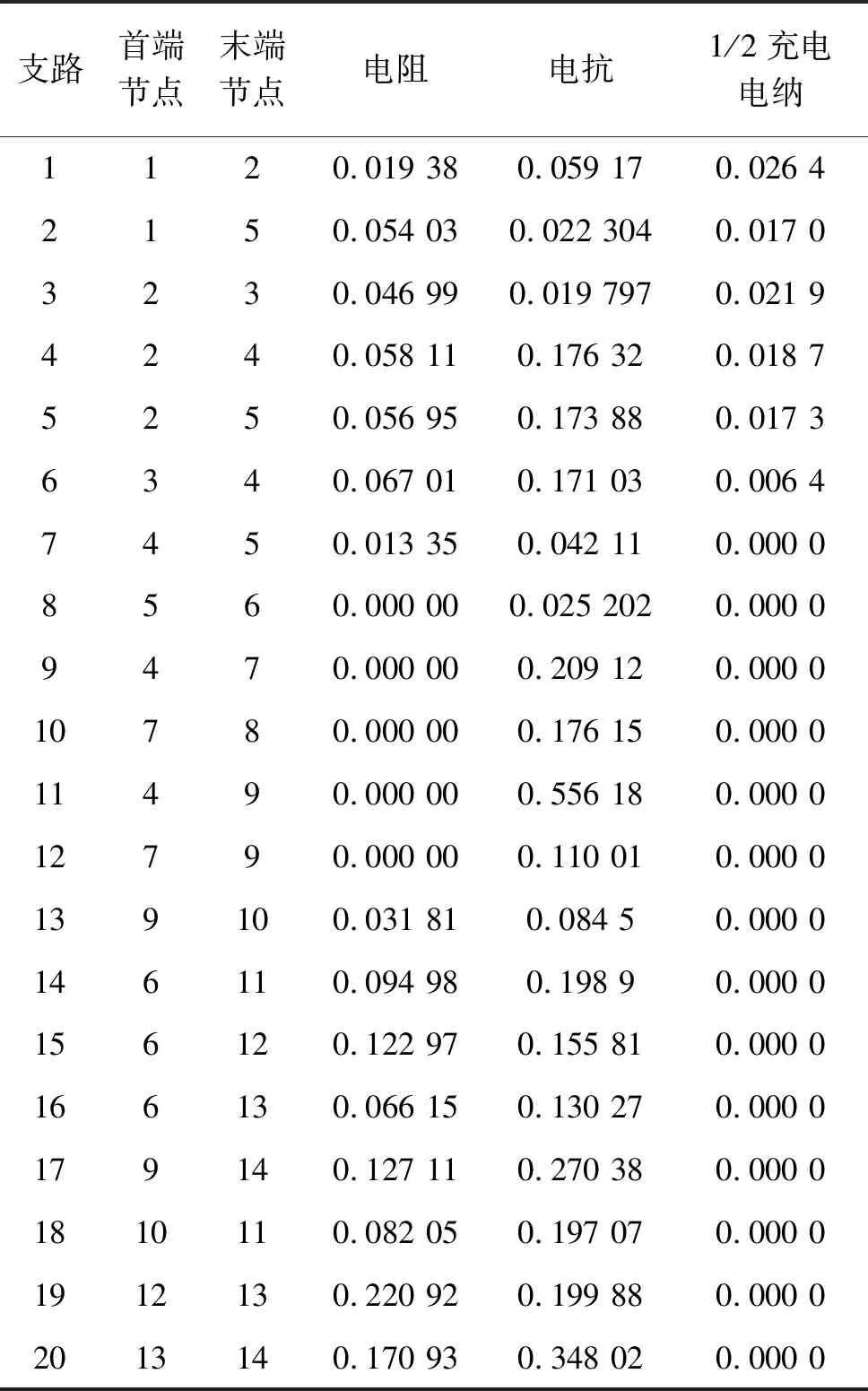
表2 IEEE14支路数据
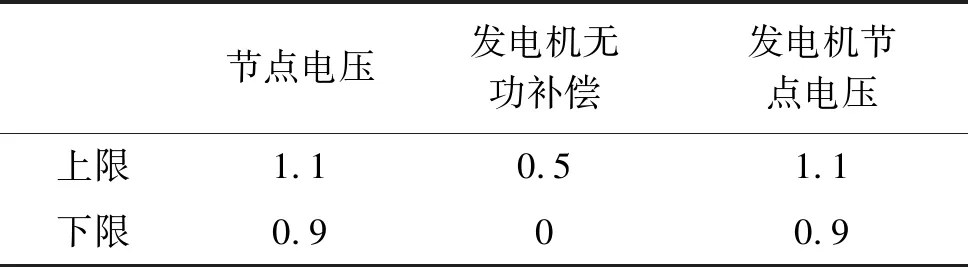
表3 数据上下限值
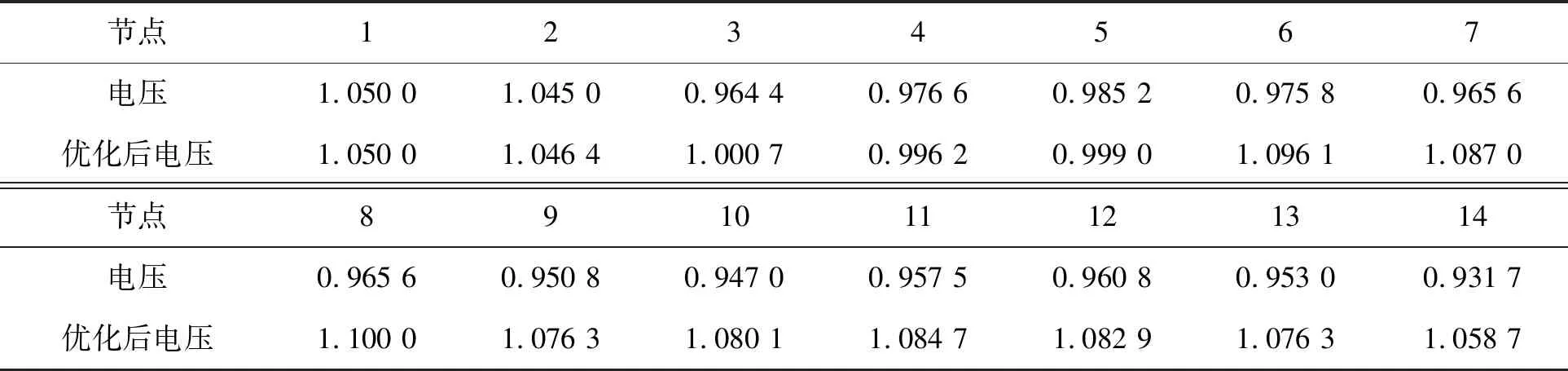
表4 优化前后电压数据
3.2 运算结果与分析
见图1,当使用基本PSO时,经MATLAB运算后,无功优化后的各个节点的电压有显著提高,网损得到降低。
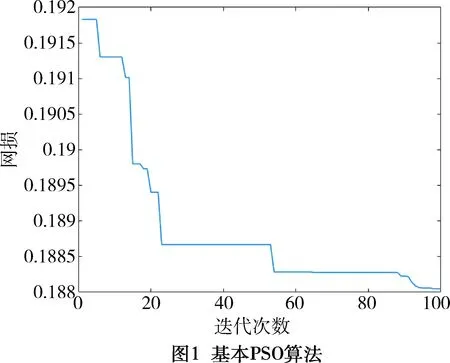
如图2,当使用改进PSO时,经MATLAB运算后,无功优化后的各个节点的电压也有显著提高,网损得到降低。同时,结果的收敛速度更快,后期基本无振荡。
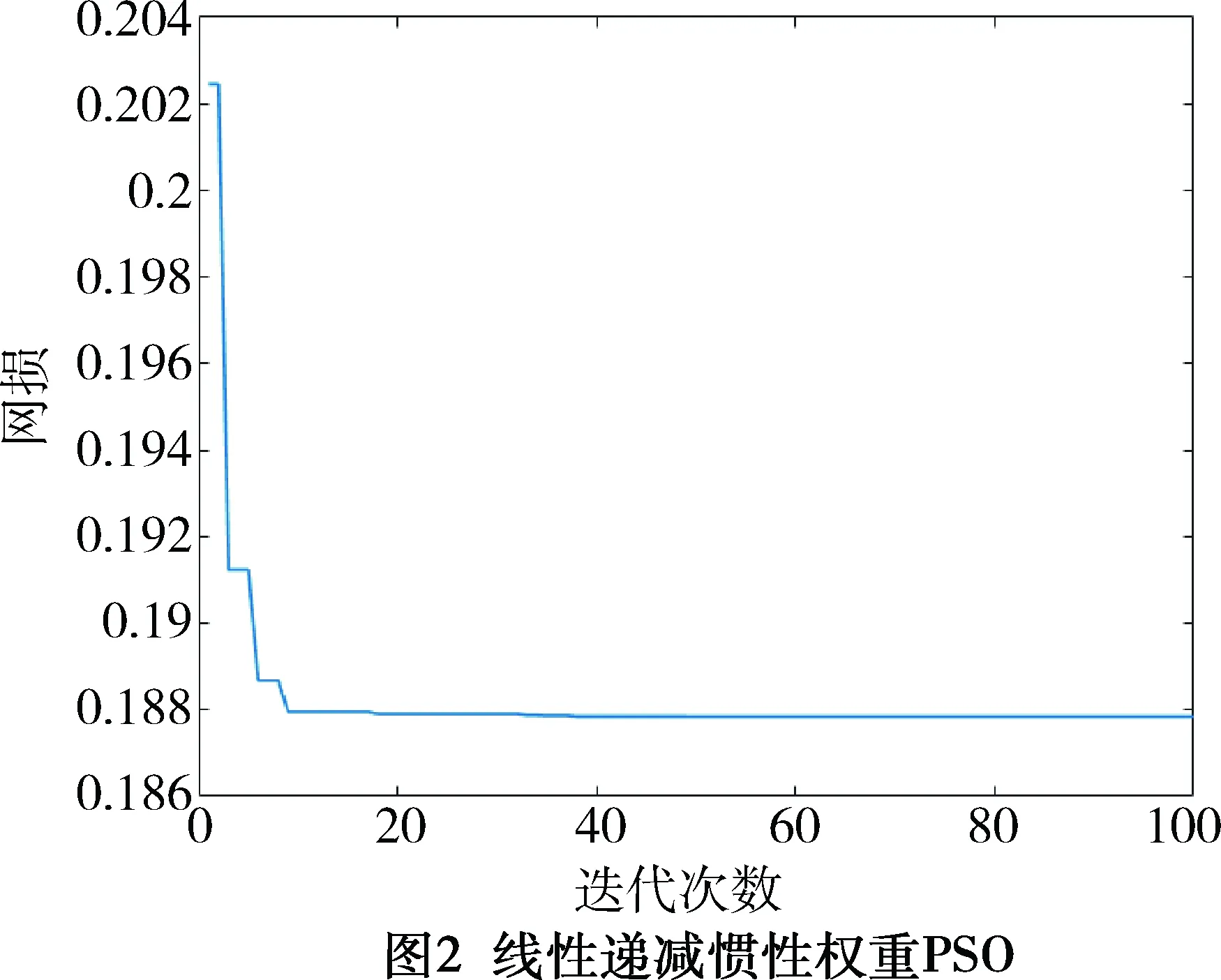
基本PSO与线性递减惯性权重的PSO两种算法对比可以得出,IEEE14节点系统的网损均由0.202 2 MW优化到了0.187 8 MW,电力系统的网损得到了降低,基本PSO后期会发生轻微震荡,而线性递减惯性权重的PSO收敛速度更快,结果更平稳。
4 结论
本文对电力系统中配电网络的无功优化进行分析研究,采用了粒子群算法建立数学模型,将粒子群算法模型与无功优化模型进行整合,从而达到降低网络损耗的目的。引入了线性递减惯性权重到粒子群算法中,使算法的收敛速度更快、结果更平稳。最后以IEEE14节点电力系统为例,使用MATLAB软件进行仿真运算,验证了本文研究方法的有效性和可行性。
