数学实验教学:趣折相似 巧生几何直观
——以“折纸中的相似”为例
2022-11-16黄晓雨江苏省淮安市淮阴中学新城校区223001
黄晓雨 (江苏省淮安市淮阴中学新城校区 223001)
纵观近几年的基础教育改革,整体虽取得了不错的成绩,但数学实验教学的发展却止步不前、举步维艰,主要原因在于教学环境、教学设备等客观条件的限制以及教师对数学实验教学的错误理解,即认为数学实验教学要在高科技教室中开展,要为学生配备先进设备等,导致数学实验教学在日常教学中难以施展.其实数学实验教学并非一定要在高科技教室、先进设备加持下展开,日常生活中的道具都可以成为数学实验教学的工具.本文通过学生动手折叠A4纸,揭示相似的理论依据,进一步认识几何直观的价值,从而提高学生几何直观的能力.
1 零起点缓坡度小步走——折线
·折叠线段,形成方法
准备活动(1)学生拿出A4纸、小尺、剪刀、铅笔等工具;(2)在A4纸上画一条任意长的线段AB.
师:请同学们动手折线段AB的垂线,并说明为什么所折的折线是线段AB的垂线.
经过小组合作交流,方法总结为:将线段AB对折(折痕两边重合),使得点A与点B重合,折痕为线段AB的垂线(图1).

图1
理由如下:取折痕上任一点D,因为对折,所以∠BOD=∠AOD.又∠BOD+∠AOD=180°,所以∠BOD=∠AOD=90°,从而OD⊥AB.
师:有理有据!这样的垂线有多少?怎么折?
生:无数条,将折痕两边的线段重合即可.
师:难度升级,请折线段AB的平行线,小组讨论如何折叠.(学生疑惑,没有思路)
师:请思考,目前要证明两条线平行,你会从哪个角度出发?
生:角!
师:那要折两线平行,纸中有没有出现角?
生:没有!但是可以作一条辅助线与线段AB相交,这样就出现了角.
师:构造的角度是多少度角比较好呢?
生:直角!因为刚才已经折过线段的直角!
经过师生互动式交流,方法总结为:先折线段AB的垂线a,再折垂线a的垂线b(不与线段AB重合),得到线段b∥线段AB(图2).
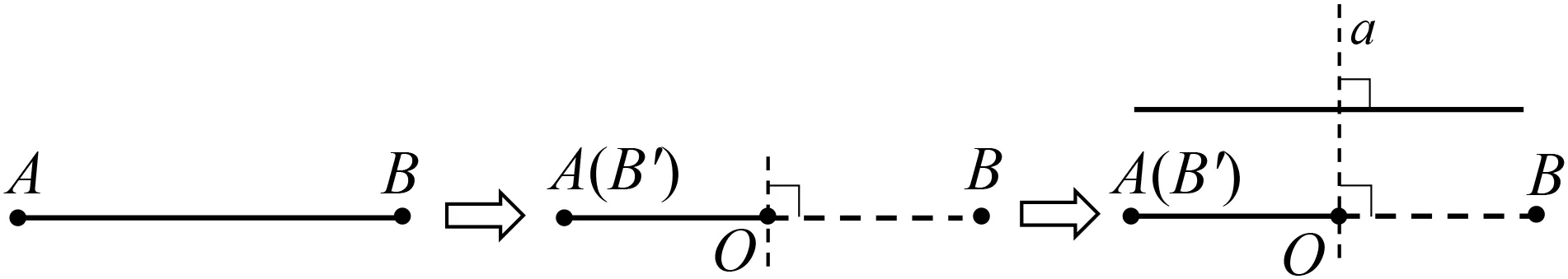
图2
师:现在在线段AB外任取一点C,如何过点C折线段AB的垂线与平行线?
生:只需让刚才折的垂线与平行线过点C即可(图3)!

图3
折线总结:(1)折一条已知线段的垂线,将折痕两端的线段重合.
(2)折一条已知线段的平行线,先折线段的垂线,再折垂线的垂线(不与已知线段重合).
2 仿操作勤督促快反馈——折三角形
·折叠图形,探索新知
准备活动:(1)将点C与点A,B分别连结,构成△ABC;(2)过点C折△ABC的高CD.

图4
生:利用刚才过点折垂线的方法,可以折出△ABC的高CD(图4).
师:取高CD的中点O,过点O折线段AB的平行线,怎么折?
生:过点O折线段CD的垂线分别交线段AC,BC于点E,F,得EF∥AB(图5).

图5
师:点E,F在线段上的位置是否特殊?
生:点E,F分别为线段AC,BC的中点,即点O为线段CD的几等分点,那么折出来的点E,F就分别是线段AC,BC的几等分点!
师:也就是说,折线段AB的平行线是否只有一种方法?
生:折等分点也可以得到平行线!
折三角形总结:(1)折已知三角形某条边的高,等价于过此边的对角顶点折此边的垂线.
(2)折已知三角形某条边的平行线:方法一,先折此边的垂线,再折垂线的垂线(不与已知线段重合).方法二,折另外两条边共顶点侧的等分点.
3 自主学勤归纳多创新——应用
·开展应用,引领拓展
准备活动(1)请学生在A4纸上折出Rt△ABC,用记号笔描出三边,标记三个顶点A,B,C;(2)再用剪刀将△ABC剪下.
问:如何折Rt△ABC的三个角,使得折出的三角形与原Rt△ABC相似?小组合作,动手操作.
经过小组讨论,折叠的思路分为两类:
思路1折“正A形”相似
①折锐角∠C(图6).
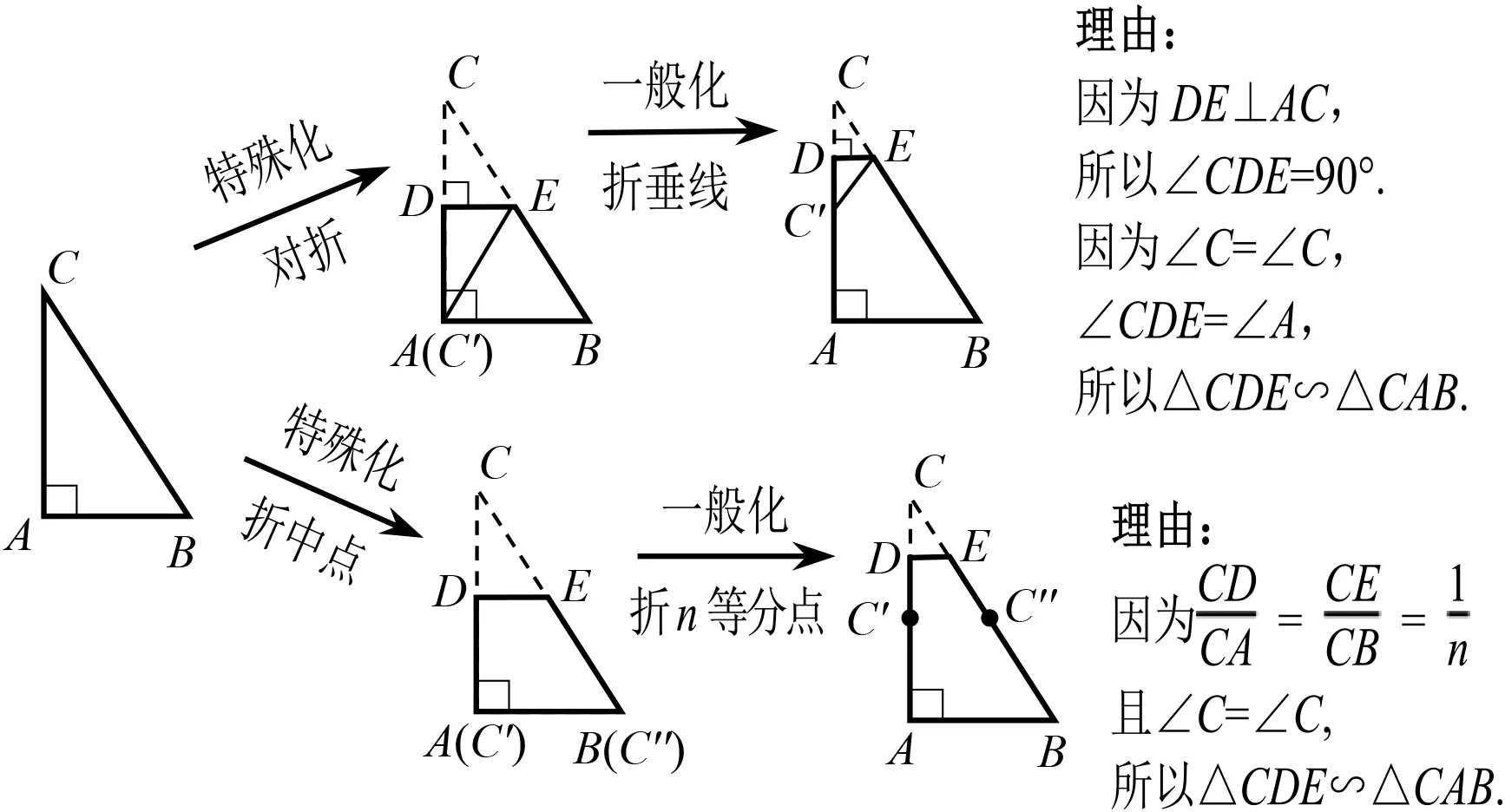
图6
②折直角∠A(方法同①).
通过折“正A形”相似发现:折“正A形”相似的本质就是折一条边的平行线.
思路2折“反A形”相似
①折锐角∠C(图7).

图7
②折直角∠A(图8).

图8
师:通过直角折“反A形”相似,有何好方法?
生:只需将直角顶点落在斜边中线上即可.
·变亦不变,不变亦变
拓展(课后作业):若将Rt△ABC变成一般的△ABC,重复上面的步骤,能否折出与原三角形相似的图形?
4 回顾与反思
本节数学实验课的目的是教会学生动手折相似三角形.若上来就让学生折一个随机三角形,然后去折它的相似三角形,很多学生会一脸茫然,无从下手.那么这节数学实验课又将变成教师主导的“灌溉课”,即教师将自己的折叠方法交给学生,学生的思维就会被禁锢,效果就会大打折扣,达不到数学实验教学的目地.因而,本节课设计得很有层次,由简入难,层层递进:利用两个基本的折纸方法作为解决问题的关键——折已知线段的垂线与折已知线段的平行线.首先通过折叠的性质以及直角度数的特殊性,得到折叠垂线的方法;其次引导学生从平行线判定的角度思考,折已知线段的交线(垂线),再通过折垂线的垂线得到折平行线的方法;然后将线段变直角三角形,折直角三角形的相似,引导学生运用两种折纸方法去观察、描述问题,理解、解决问题.学生把理论与实践相结合,通过所学的相似判定结合刚才的折纸方法,发现折直角三角形相似就是折垂线或折平行线,从而揭示本实验操作的本质,甚至部分学生还将方法进行了拓展创新(折角平分线以及折斜边中线),积累了数学活动经验,促进了几何直观发展.本节课设计的巧妙之处在于将一般性三角形先强化条件变成直角三角形,通过折直角三角形相似发现,只需要折直角(折角等)就可以得到相似;进而再将折相似弱化成折一边的垂线或平行线;最后将问题回归原始,折一般性三角形的相似,学生就可以利用之前所学顺利解决此问题.课堂的教学自始至终都是学生自己动手操作,发现方法,得出结论,解决问题.很好地培养了学生动手操作、理论与实际结合、解决问题的能力和探索的精神,有效地将“听”转变为“学”的方式,从“实物直观”“图形直观”的角度发展了学生的几何直观.
数学实验的本质是一种学习方式,即学生运用有关工具(如纸张、剪刀、模型、测量工具、作图工具以及计算机等),通过动手动脑“做”数学的数学学习方式,这种学习方式不是简单地让学生被动式接受教科书上或者教师所讲授的现成结论,而是让学生从自己已有的“数学知识”出发,变“听数学”为“做数学”,变“看演示”为“动手操作”,变“机械接受”为“主动探索”.“做实验”的主动探究过程培养了学生的动手实践能力、解决问题能力和创新意识,积累基本活动经验,进而有效转变初中数学教与学的方式.
学生在折叠实验课中,通过“折相似”的本质感悟到“化繁为简”的重要思想.但是,将“折相似”的实验活动弱化成折线段的垂线或平行线,再利用这两种方法来“折相似”,这对于学生而言是有一定难度的.这需要学生具有一定的几何直观能力,能够利用图形的本质描述与分析问题,借助几何直观把复杂的图形变得简单明了.对于学生而言,这是一个循序渐进的学习过程,在这个过程中,教师应给予学生充分的信任,给予学生更多时间和机会来展示交流,真正实现教学相长.
