初中数学“整体法”解题思路分析
2022-11-16陈宇
陈 宇
(江苏省南通市幸福中学,江苏南通,226001)
整体法是初中数学中常用的一种解题方法,这种方法将问题看作一个完整的整体,注重问题的整体结构和结构改造,特点是可以宏观上全面观察事物的整体结构,从而揭示事物的本质[1].初中数学和高中以及小学数学有着很大的不同,小学数学更多地注重学生的逆向思维,高中数学更侧重于学生正向思考并解决问题,而初中数学则需要完成这个过渡.初中数学有很多种解决的方法,而方法的选取决定了解题的上限,运用好的解题方式可以更加方便快捷.整体法就是解决初中部分数学问题的一种非常便利的方法.灵活运用整体法可以提高数学分析能力和解决能力.整体法在初中数学的应用主要可以从以下几个方面进行展开.
1 整体法在代数式求值中的应用
代数式求值是初中数学中最为重要的知识点,在解决此类问题时,利用整体法可以有效进行化简求值,其中整体代入可以更快捷地解决部分问题.整体代入的解题思路是将一个代数式作为一个整体,然后将这个整体的值代入到另一个代数式中进行运算,具体案例如下:
例1已知a2+5ab=16,并且3b2+2ab=50,求a2+11ab+9b2的值.
题目中出现两个未知数a和b,在正常的解题中,需要通过两个代数式结合计算出a和b相对应的代数值,再代入到最后所要计算的代数式中进行解析,计算起来相对繁琐.
现采用整体法对这道题进行解题分析,首先将两个代数式a2+5ab=16和3b2+2ab=50看作两个整体A和B进行分析,然后可以发现最后所求的代数式a2+11ab+9b2,可以由一个整体A和三个整体B进行相加得到,即a2+11ab+9b2=(a2+5ab)+3×(3b2+2ab),因此可以很方便地求出最后的函数值为166.
因此,在解题时,学生的思路应该时刻保持清晰,能够准确地把握题中的要点,结合整体法的思路对代数问题进行分析,找到解决问题的捷径,进而快速准确地完成解题.
2 整体法在因式分解中的应用
整体法在函数中的运用还可以体现在初中数学最重要的解题要点——因式分解中,因式分解在很大程度上运用了数学的整体思想,把重点放在问题的整体上,多方位思考,进行整体变形,多角度探究,最终确定解题的策略,进而解决问题.
例2分解因式(x+1)(x+2)(x+3)(x+6)+x2
题干中可以发现如果将每一个括号内的代数式分别进行相乘最后再进行分解因式会显得非常困难,这里我们可以进行分组,当(x+1)和(x+6)相乘以及(x+2)和(x+3)相乘可以得到相似的内容,因此可以先将这两部分进行组合计算,得到的展开式再利用整体进行运算即可,具体的解题过程如下:
解:原式=(x+1)(x+2)(x+3)(x+6)+x2
=(x+1)(x+6)(x+2)(x+3)+x2
=(x2+7x+6)(x2+5x+6)+x2.
设(x2+6x+6)为a,
那么原式=(a+x)(a-x)+x2
=a2-x2+x2
=a2
=(x2+6x+6)2.
通过上述问题的解决,可以发现因式分解的过程中应该特别注意整体法的应用,结合整体代入的方法,不仅可以简化运算,而且能够有效地避免由繁琐的运算带来的弊端.将部分算式看作整体,在实际解题中有着很大的作用.
3 整体法在解方程中的应用
初中数学离不开方程的运用,解方程的题目类型多种多样.很多解方程的问题,也会运用到整体法,在解方程的过程中,韦达定理对于学生一定不会陌生,这种利用根的性质所运用的定理,同样利用了整体法的性质,从而使问题更加容易解决.
例3若m是方程2x2-3x-1=0的一个根,则6m2-9m+2 022的值是多少?
题目中可知m是方程的一个根,因此将m代入到方程中,一定成立,而代入后通过比较已知方程和需要求解的方程,会发现二者存在数量关系,然后利用整体法直接代入可以得出所求方程的值.利用整体法可以免去计算未知数的值,整体代入求出所需值,提高了准确性.
解:2x2-3x-1=0
则2x2-3x=1,
将m代入可得2m2-3m=1,
原式=6m2-9m+2 022
=3×(2m2-3m)+2 022
=3+2 022
=2 025.
通过上述方程的解决,可以发现,合理地运用整体法的知识可以解决很多解方程的问题.计算过程中,对问题整体化考虑,可以将问题简洁化,有时甚至可以不计算未知数的值就可以解出所需结果.在教学过程中要注意到学生使用整体法寻找最优解题的路径,这可以拓宽学生的知识面,同时培养学生的发散思维.
4 整体法在分式方程组中的应用
处理部分分式方程组时,对方程组直接进行赋值计算会比较麻烦.这些较为复杂的方程组利用常规的计算既浪费时间,又容易出错.如果可以利用整体法对问题进行简化处理,然后再进行计算会使问题的解决变得更加容易.
例4甲、乙二人合作完成一项工程需要24天;若乙先干10天后甲再加入,则需要花费20天完成,问甲,乙单独完成这项工程各需要多少天?
面对这类问题,首先想到的就是列方程组进行计算,接着进行解方程分别计算出甲、乙完成这项工程需要花费多少天即可.真正解题时会发现所得方程组为分式方程组,这时如果利用传统解方程组的方法,并不容易求解,因此需要灵活变通,找到便捷的解题路径,做到解题省时又省力.该题利用整体法就可以很好地解决,求解过程与分析如下:
解:首先需要假设甲、乙单独完成这项工程各需要x天以及y天.
这时可以得到如下方程组
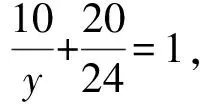
通过上述问题的解决,可以发现整体法在处理分式方程组的便捷之处.在实际教学工作中,教师应渗透整体的思想方法,提高学生的解题效率.
5 整体法在几何问题中的应用
初中几何问题是初中数学的难点,解决此类问题的困难之处在于做辅助线进行分析,但辅助线的选取对于学生来说是一个巨大的考验,整体法同样适用于解决此类问题.解决初中几何问题经常会用到的方法就是整体补形法,这是整体法的一个分类.利用整体补形法对几何问题进行分析,通过补形还原整体图形的原有状态,可以有效训练学生的整体性思维,从而更好地对问题进行分析处理.

例5如图,四边形ABCD中,AB=2,BC=1,CD=1,∠ABC=120°,∠BCD=90°,求四边形ABCD的面积.
从图中我们可以发现,由于四边形ABCD是一个不规则的四边形,想要直接求出四边形ABCD的面积是很难做到的.那么要想求出它的面积,首先就要进行组合或者拆分,将其转化为熟悉的规则四边形的面积.因此就需要利用整体补形法对其进行补形,然后再进行计算,具体解题思路和方法如下:
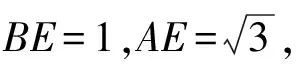
初中几何问题中,利用辅助线解决问题是难点也是重点.大部分题目都是缺失辅助线导致很难分析,间接考虑这个问题就会发现,添加辅助线在大多数情况下都是在利用整体补形法将缺失部分补全,从而还原本身图形进行分析.因此,学生掌握整体法的思维模式是解决几何问题的重中之重.掌握好整体法的思路,会极大提高学生的空间想象能力,对于学生的解题技巧同样会有所提高.同时,几何问题对于学生们的智力开发也起到了非常大的积极作用,利用好整体法解决问题可以增加学生的学习兴趣,除此之外,合理运用整体法进行解题也会使得不易解决的几何问题更加清晰明了.
6 整体法在逻辑思维问题中的应用
整体法在一些思维逻辑问题上同样可以起到意想不到的效果.在面临很多相对复杂的问题时,将问题步骤细化会导致思考量增大,解决问题相对也不容易,但利用整体法思考,抛弃中间的步骤,将问题简化,反而会有更好的成效.
例6王师傅开店,一双鞋进价为30元,甩卖20元,顾客买鞋给了50元,王师傅找邻居换了50元,事后邻居发现这是假币,王师傅又赔给邻居50元,问王师傅亏了多少钱.
这个问题看似很简单,但很多人都会走入误区.很多学生习惯于把这个问题分开考虑,将问题细化到每一个交易环节,反而会使头绪出现问题,最后出现错算,少算以及误算的情况.将问题进行整体分析,会发现在全部的交易中,导致王师傅亏损的只有甩卖以及收假币两个环节,其他部分找零钱以及换钱等环节都是平等交易,不涉及亏损,因此通过整体法分析,发现只存在假币50元以及甩卖所赔10元,共计亏损60元.
通过上述问题,可以发现,很多思维逻辑问题都是给学生创造误区,让学生追求分析每一个步骤,反而忽略了问题的本身,做了大量无用功.而合理运用整体法,一方面可以帮助学生将复杂的逻辑梳理清楚,另一方面可以帮助学生对问题有更深层次的理解.能否将复杂的问题简单化处理是一个学生的逻辑思维水平的重要体现.
7 整体法对于初中数学教学思考
在初中数学的教学中,整体法可以让学生在解答各种类型问题的过程中,对所了解的知识内容进行整体分析和研究,可以有效提高解题的正确率和效率[2].初中数学的教学过程是一个漫长的过程,它需要老师和学生的紧密配合.解决问题的方法有很多种,整体法只是研究问题的其中一个方法,但整体法的应用,不拘泥于常规的解题思路,它可以更深层次地帮助学生建立做题的思维模式.
在对于初中数学习题的分析过程中,整体法一直都扮演着一个特殊的角色,它不仅仅是一种解题的策略,更是一种对于学生能力培养的有效方法.熟练运用整体法最大的优势依然在于计算时间上的节省以及解题准确率上的大幅提高.
对于学生亦或是教师而言,数学是一个美丽的学科,是一个有魅力的学科,它最让人流连忘返的地方在于它的多样性,每道题的解题方法都不单单是某一种,整体法在庞大的初中数学解题方法中,也不过是冰山一角.很多学生会把这种方法当作投机取巧而不屑一顾,因为它似乎与传统数学枯燥复杂烧脑的解题手段格格不入,但是整体法的灵活运用,摒弃了那些冗长繁琐的步骤,它如同生活中“大道至简”的理论一样,将问题化繁从简,更应该是初中数学教学发展的方向.
总而言之,整体法在初中数学的学习中是一种非常重要的学习方法.在解题方面,它可以提高学生解题的效率和能力,让学生可以在题干中找到问题的关键点,把握住总体视角,也让学生的解题思路更加清晰明确,省时省力的同时也提高了解决复杂问题的准确性.在教学方面,整体法的教学应该更高水准地应用于初中数学教学中,让它不仅仅作为解题的一种手段.教师要能通过这种方法,提高学生的分析思考能力,构造学生的空间想象力,引导学生举一反三,灵活运用所学到的知识,积累更多的经验,实现一题一解.一题多解至一题优解的转化.
