直螺栓连接预制综合管廊刚度计算方法

2022-11-16邓博团申超凡

科学技术与工程 2022年29期

邓博团, 申超凡

(西安科技大学建筑与土木工程学院, 西安 710054)

地下综合管廊是保障城市运行的重要基础设施，基本采用传统现浇或预制拼装两种施工方法。预制拼装综合管廊，其主体结构构件由预制厂制作，而后在施工现场拼装成型，具有工期短、成本低、施工效率高、环境污染小等优势，为综合管廊的应用和推广提供了条件。

以往研究表明，预制混凝土结构受接缝影响，受力性能不同于现浇结构，接头的存在使结构刚度分布不均，故其所受内力和形变也随之变化[1]。在盾构隧道预制衬砌接头上，国内外学者已经取得了一定研究成果[2-4]，就隧道结构受力变形的理论中，由日本学者志波由纪夫等[5]提出的纵向等效连续化模型运用最为广泛，之后为使该模型能够更准确地运用于具体工况中，一些学者又通过对横向性能[6]、螺栓预应力[7]和环缝影响[8]等因素的考虑及对这些因素的综合考虑[9-10]，对该模型进行了改进。类矩形截面隧道近些年已经在一些工程中得以应用[11]，一些研究中同样引用了该模型，郑庆坂等[12]对大断面矩形盾构隧道等效抗弯刚度进行了研究；黄亮等[13]、梁荣柱等[14]等推导得到了类矩形盾构隧道的纵向等效抗弯刚度解析解，并对其影响因素进行探究。在预制管廊中，胡翔等[15]通过单调静力试验，对预应力筋连接的预制管廊其接头刚度和受力特征进行了研究；王鹏宇等[16]通过对预制管廊横向接头受力性能进行研究，提出了能够对管廊横向接头承载力和刚度进行分析的计算模型。

随着隧道建设技术的完善，在盾构隧道中的相关研究已取得一些成果。相较隧道衬砌，管廊接头的研究相对较少，且大多仅是以单个接头为研究对象，研究接头刚度，或是在管廊受力破坏过程中接头的受力变形状态，未明确揭示接头的存在对管廊整体刚度的影响。因此现将采用盾构隧道管片相关计算方法，对直螺栓连接的预制拼装管廊其纵向刚度进行研究。以期得到直螺栓连接预制管廊的纵向等效刚度，以及其在极限弯矩作用下，截面最大拉压应力、接头最大变形、接头螺栓最大拉应力和接头螺栓最大变形的表达式。

1 隧道结构纵向计算模型

目前对盾构隧道管片纵向受力性能的研究主要有纵向梁-弹簧模型、梁-接头模型和纵向等效连续化模型。

1.1 纵向梁-弹簧模型

小泉淳等[17]日本学者提出，用梁单元对地铁盾构隧道纵向管节进行模拟，用弹簧来模拟结构的环向、纵向接头以及土体与隧道的相互作用。采用该模型可得到盾构隧道的纵向等效刚度，计算公式为

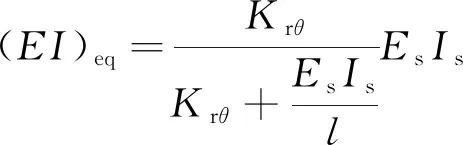
(1)

式(1)中：Krθ为管片环缝转动刚度；Es为隧道截面弹性模量；Is为隧道截面惯性矩；l为两环管片中心线间的距离。

1.2 梁-接头模型

由朱合华等[18]提出，该模型与梁-弹簧模型相似，区别在于对接头的处理，使用双节点接头对管片接头进行模拟、管段间接头用弹簧进行模拟。通过使用该模型能够得到盾构隧道相邻管片的不连续变形量，在模拟其纵向非线性变形上表现良好。

1.3 纵向等效连续化模型

志波由纪夫等[5]日本学者提出，该模型将隧道截面拟作均质圆环，纵向上等效为具有均匀刚度的连续梁，该模型常被用于盾构隧道纵向性能分析中。

纵向梁-弹簧模型实质是将有环缝的管片结构纵向折减刚度后等效为均质结构。该模型能够很好地模拟弹性地基上梁的纵向受力情况，但其建立需以卡式第二定理为基础，只适用于线弹性小变形情况，不能准确模拟管片与接头的非线性效应[19]。梁-接头模型虽可以很好地模拟接头的非线性效应，但该模型分析结构与预制管廊存在较大差异，不适用于管廊纵向刚度计算中。纵向等效连续化模型虽能较好适应预制管廊结构，但其过于理想化，螺栓预应力、环缝影响范围、横向刚度等因素均未予以考虑[10]。预制管廊的接头螺栓多为高强螺栓，预应力的施加可有效保证接缝闭合的紧密性，减少施工结束后及使用过程中由于变形引起的接头张开，同时对管廊纵向性能也有一定影响。在对管廊纵向刚度研究中，螺栓预应力这一影响因素不容忽视。将采用考虑螺栓预应力因素的纵向等效连续化模型，对直螺栓连接预制管廊纵向刚度进行研究。

2 直螺栓连接预制管廊纵向等效刚度计算

2.1 模型的建立

等效连续化模型是从横向、纵向两方向折减盾构管片的受力，现以等效连续化模型为基础，将建立适用于直螺栓连接预制预应力管廊的模型。按照等效连续化理论，将存在纵向接头的预制管廊简化为纵向连续均匀的矩形框架梁，通过对其刚度进行折减使其与原结构得以等效。在等效刚度计算中，做如下假设。

(1)当预制管廊受压时，认为压力全部由混凝土结构承担。

(2)当预制管廊结构受拉时，认为该状态下混凝土节段与接头螺栓都参与变形，且螺栓均匀分布于接头截面处。

(3)当结构承受弯矩时，以中性轴为界，受压侧只考虑混凝土变形，受拉侧混凝土和接头螺栓共同参与变形，且符合平截面假定。

根据以上假设进行模型的建立，该模型将预制结构与纵向接头综合考虑，使预制管廊结构与模拟的均质梁等效刚度相同，所模拟模型由弹性基础支撑。计算示意图如图1所示，仅对该模型拉伸、压缩和弯曲状况进行研究。

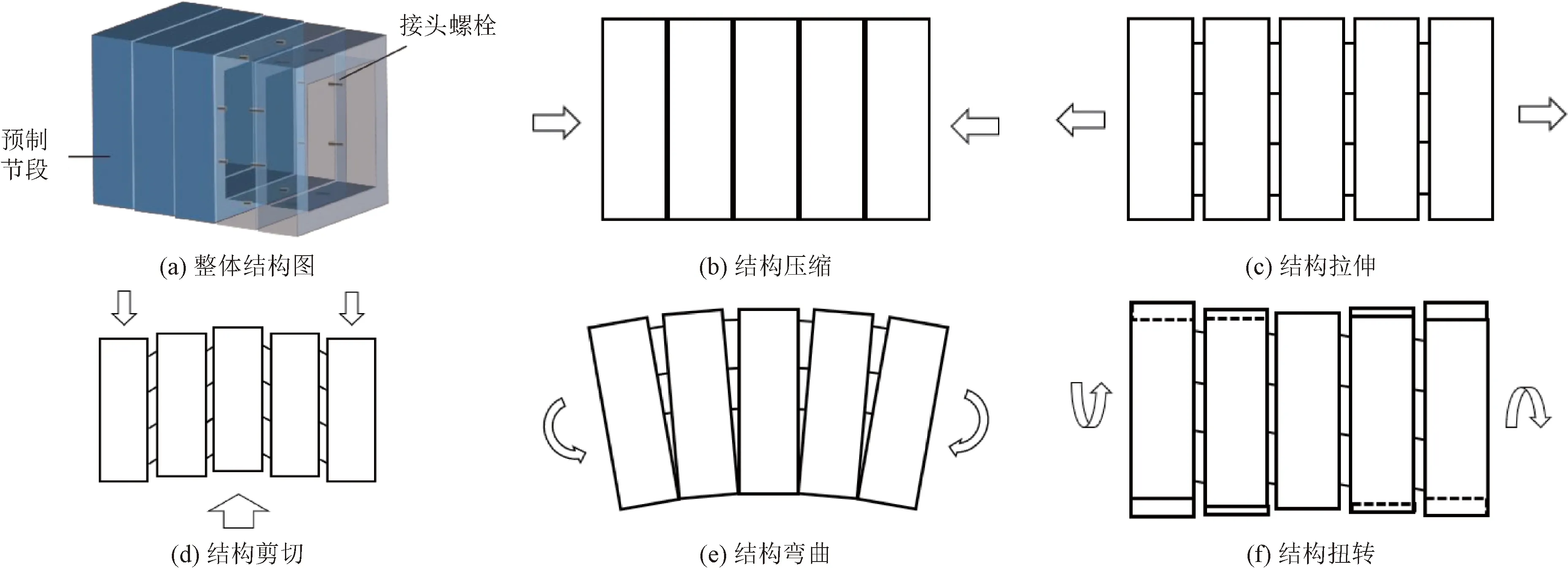
图1 模型纵向变形示意图

2.2 螺栓预应力的影响

在考虑螺栓预应力对管廊拉压刚度的影响时，认为螺栓预应力是作用在螺栓上的初始外力。即螺栓的应力应变是预应力和外力作用效果的叠加，变形曲线如图2所示。

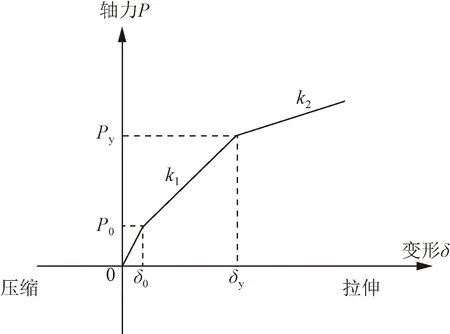
k1、k2分别为螺栓的弹性、塑性刚度系数，k1=EA/l，k2=ak1，a为螺栓的塑性弹性刚度比；E、A、l分别为单个螺栓的弹性模量、截面面积和长度；P0为螺栓预应力；δ0为预应力作用(初始状态)下螺栓的变形；Py为螺栓弹性极限拉力、极栓伸长量

2.3 等效轴向刚度

两节连续预制管段各取一半，为一个计算单元，总长度为ls。当单元所受拉力小于预应力时，预制结构受拉变形；所受拉力大于预应力时，螺栓也参与受拉变形。单元受压时,所受压力全部由预制结构承受，预制结构受压变形。结构单元受力变形关系为

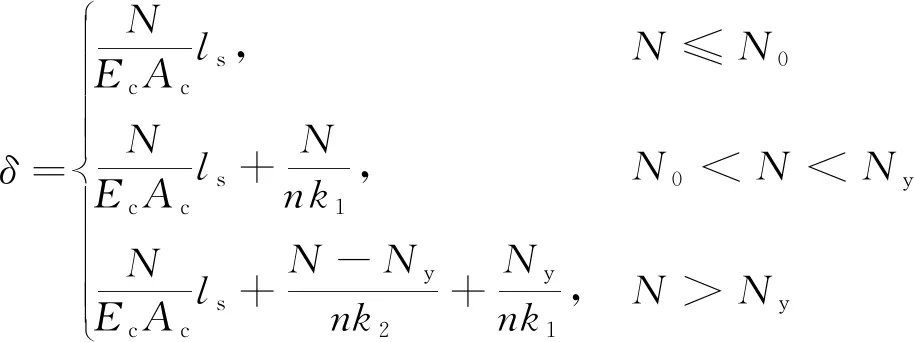
(2)

式(2)中：N为单元所受的轴力；N0为接头处的总预应力，N0=nP0；Ny为接头处的弹性极限拉力，Ny=nPy；P0为单个螺栓的预应力；Py为单个螺栓的弹性极限拉力；n为接头处螺栓的数量；k1、k2为单根螺栓的弹性、塑性刚度系数；δ为计算单元的变形量；Ec为预制结构的弹性模量；Ac为管廊截面面积；ls为管廊节段长度。

所建立的模型受轴力作用时的变形量可表示为

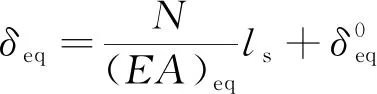
(3)

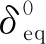
由螺栓的变形特性，易得

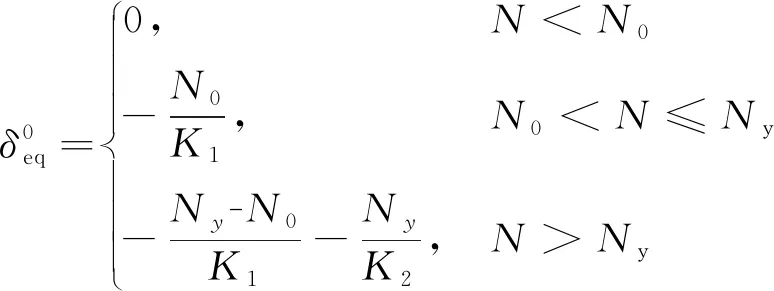
(4)

式(4)中：K1、K2分别为接头的弹性、塑性弹簧刚度系数，K1=nk1，K2=nk2。

根据式(3)、式(4)，得到螺栓连接的预制管廊其等效拉压刚度为

(5)

根据所求做出管廊结构等效轴向刚度示意图，如图3所示。管廊结构轴向受力产生变形可简单分为3种情况：①当管廊受轴向压力或者小于总预应力的拉力时，其变形遵循等效压缩刚度；②当管廊受轴向拉力超过总预应力，管廊结构以等效弹性刚度变形；③随着轴力达到接头的弹性极限拉力，管廊结构变形遵循其等效塑性刚度。

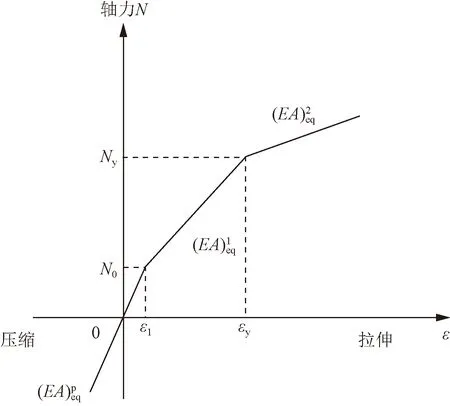
图3 管廊等效轴向刚度

2.4 等效弹性弯曲刚度

以只存在纵向接头的单舱节段预制管廊为例，对其进行弯曲刚度分析。接头螺栓两端管廊各取一半长度作为一个计算单元，总长度为ls。管廊两端在弯矩M作用下发生弯曲，相邻节段管廊中心线延长相交形成转角θ，欲求M与θ的关系，增设如下假设。

(1)管廊的中性轴位置和截面应力情况在纵向上保持一致。

(2)为计算方便，按连续分布处理沿矩形框截面离散分布的螺栓，认为管廊壁四面厚度平顺，忽略管廊腋角。

节段预制管廊受弯变形示意图如图4所示。在弯矩M作用下，结构中各个螺栓的受力变形均在弹性范围内，即整个结构处于弹性状态。将对其所受弯矩M与发生的转角θ的关系进行求解，图5为计算单元弹性状态的应力应变图。

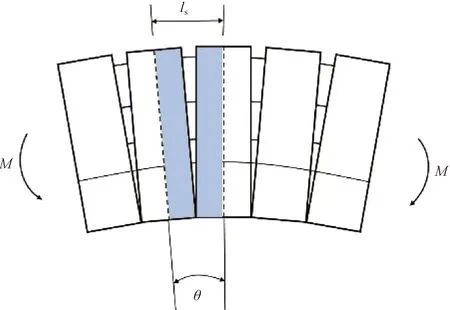
图4 受弯变形示意图

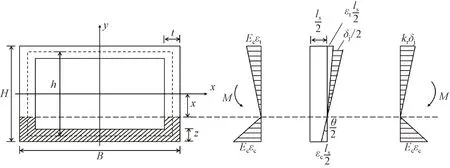
H为管廊截面的高度；B为管廊截面的宽度；h为管廊上下侧螺栓距离；t为管廊截面侧壁厚度；z为管廊截面上下壁厚度；x为中性轴距截面中心线距离；δj为距中性轴最远处螺栓的变形；εt、εc分别为截面的拉应变和压应变；θ为截面转角；Kr为螺栓平均线弹性刚度，Kr=K1/2(h+B-t)

根据变形协调条件得

(6)

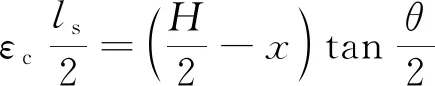
(7)

当θ较小时，上述方程可简化为

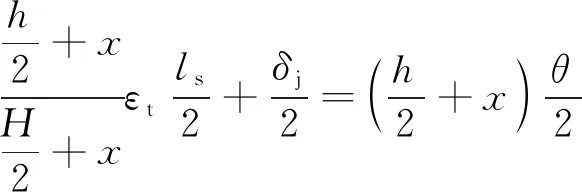
(8)

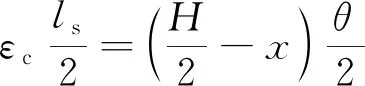
(9)

根据力的平衡条件有

(10)

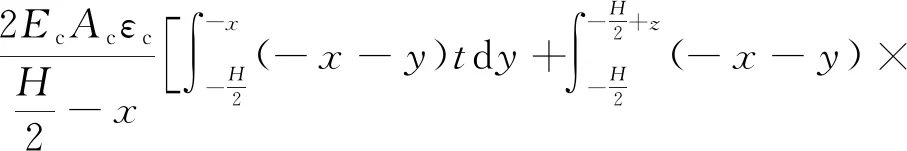
(11)

由式(8)～式(11)可以解得中性轴的位置x满足的关系式为

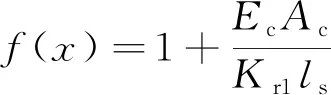
(12)

式(12)中：

根据弯矩平衡条件有

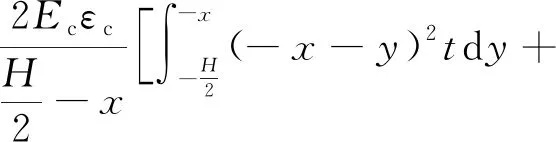
(13)

由式(8)～式(13)解得截面转角θ为

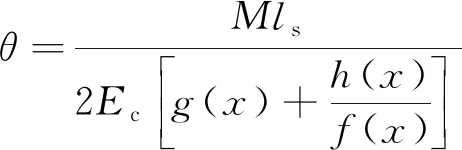
(14)

式(14)中：

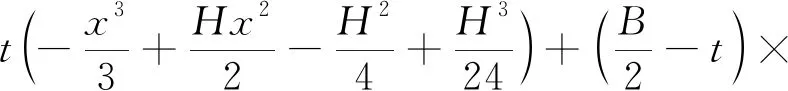
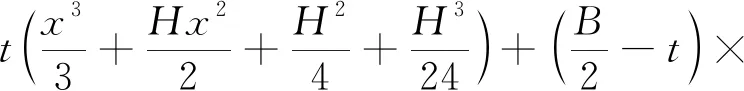
由单跨直梁的转角公式，易得等效梁受弯矩作用时符合的关系式为

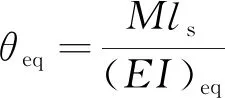
(15)

对比式(14)、式(15)，得出预制管廊的等效弹性弯曲刚度为

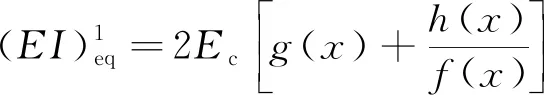
(16)

接头处螺栓所受拉力随弯矩增加而增加，当有螺栓达到屈服时，计算单元也随即进入屈服状态，此时的弯矩即为预制管廊的弹性极限弯矩。在即将进入屈服状态时，预制管廊的最大形变为距离中性轴最远处的变形，也即该处螺栓的变形，表达式为

(17)

由式(17)可得管廊弹性极限弯矩为

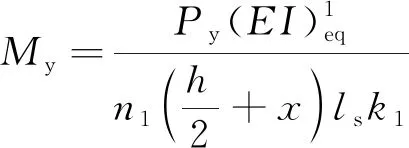
(18)

式(18)中：n1为距中性轴最远处螺栓数量。

考虑螺栓预应力影响为

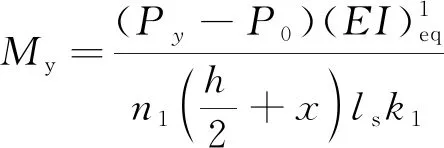
(19)

将式(14)代入式(9)，对螺栓预应力予以考虑，得到截面处最大压应力为

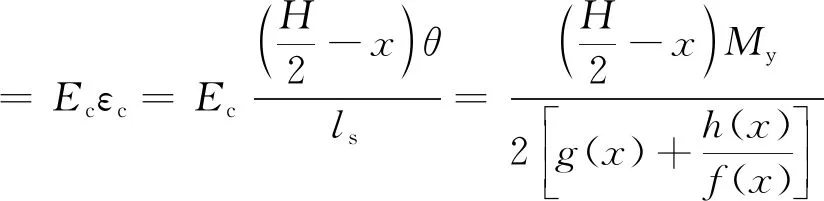
(20)

截面处最大拉应力为

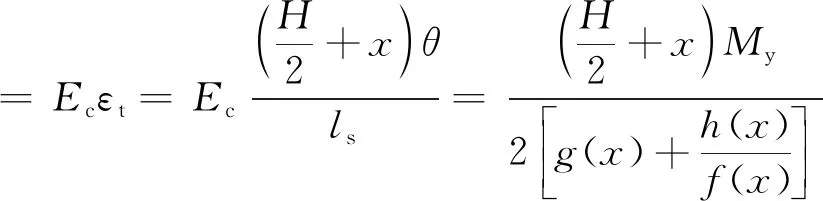
(21)

接头的最大变形为

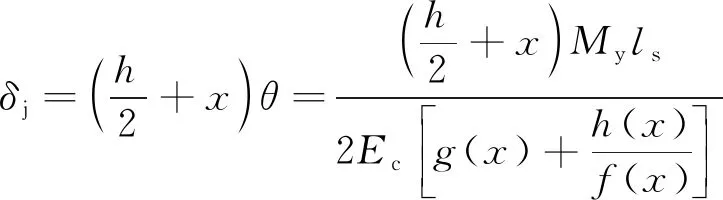
(22)

接头螺栓最大拉力为

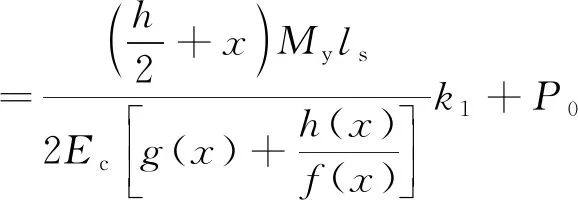
(23)

接头螺栓的最大变形为

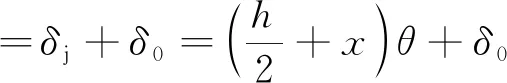
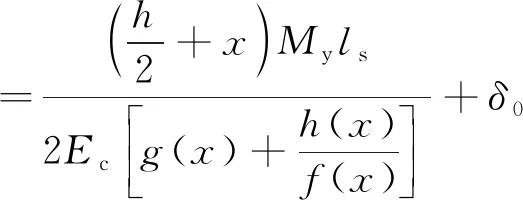
(24)

2.5 纵向等效抗弯刚度有效率

在研究预制管廊纵向等效刚度中，为了便于对管廊纵向刚度进行指标化分析，引入纵向等效抗弯刚度有效率，后简称为刚度有效率，表达式为

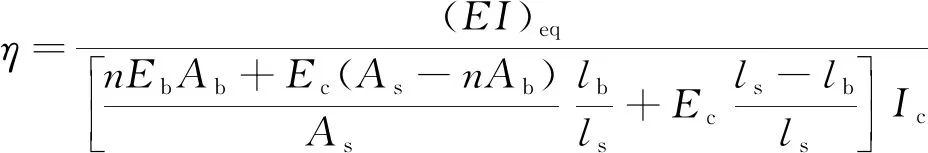
(25)

3 基于工程实例的预制管廊有效刚度分析

参考文献[20]中的相关数据，利用推导得到的解析公式，分析相关因素对弹性状态下预制管廊等效抗弯刚度的影响规律。表1为预制管廊截面设计参数，表2为接头设计参数。

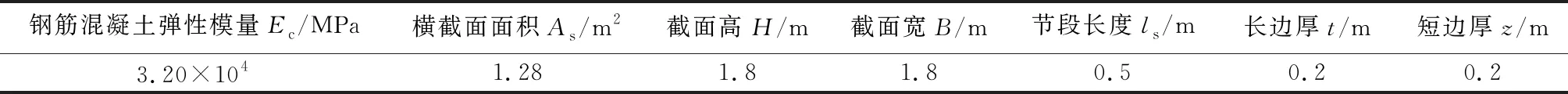
表1 截面设计参数

表2 接头设计参数

3.1 截面宽高比的影响

根据已有的参数，结合前文推导的刚度计算公式，固定截面高H，改变截面宽B，使得截面宽高比B/H在0.5～2.0变化，即H=1.8 m不变，使B在0.9～3.6 m变化，求出对应的中性轴与截面中心线距离(后简称为中性轴位置)x和刚度有效率η，描点连线，绘制成图6。

由图6可知，当宽高比B/H由0.5增加到2时，η由2.716迅速降低为原来的30.78%，最终停在0.836。B/H在0.5～1区间内增长时，其变化趋势较快，当宽高比由1增加到2时，尤其在1.5～2的区间内，η变化趋于平缓。截面宽度在较小范围内变化，尤其在宽高比较小的情况下，会引起刚度有效率大幅变动，在实际工程中，管廊预制件矩形截面尺寸设计中宽高比的影响不容忽视。

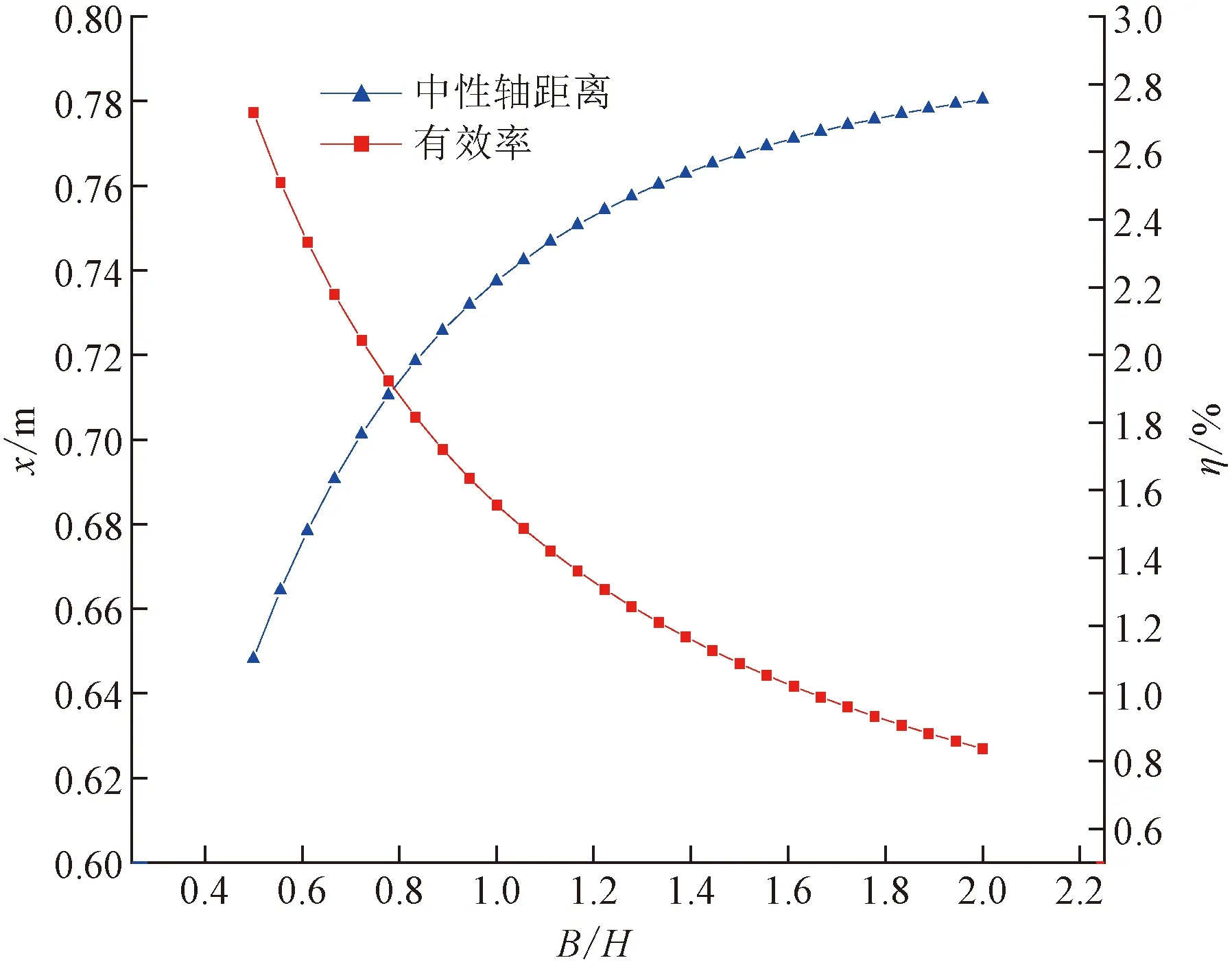
图6 刚度有效率及中性轴位置与截面宽高比之间关系

随着截面宽高比由0.5增加到2，中性轴位置x由0.648 m增加到0.780 m，增长20.37%，变化趋势由急到缓。即随着宽高比的增加，中性轴逐渐靠近截面下缘，截面受拉面积较大且仍在增加，结构受力状态越来越差。由此表明，在管廊截面尺寸设计中，应避免过大的宽高比。

3.2 管廊壁厚度的影响

设管廊截面壁厚均匀，即长边壁厚t与短边壁厚z相等，令管廊壁厚度t从0.1 m增至0.3 m，z=t，其他参数不变，求出管壁厚度变化过程中对应的中性轴位置x和刚度有效率η，并绘制关系曲线，如图7所示。

通过图7可看出，中性轴位置x随管壁厚度t的增加先增后减，当t由0.1 m增至0.15 m时，x由0.734 m降至0.743 m，降低1.23%；当t为0.15 m时x出现峰值0.743 m；当t由0.15 m增至0.3 m时，x由0.743 m降至0.714 m，降低3.90%，整体变化较平缓，表明管壁厚度对截面受力影响较小。当t=0.15 m时峰值出现，表明此时中性轴距离截面中心线最远，截面受压面积最小，受力状态不好，设计中应避免。

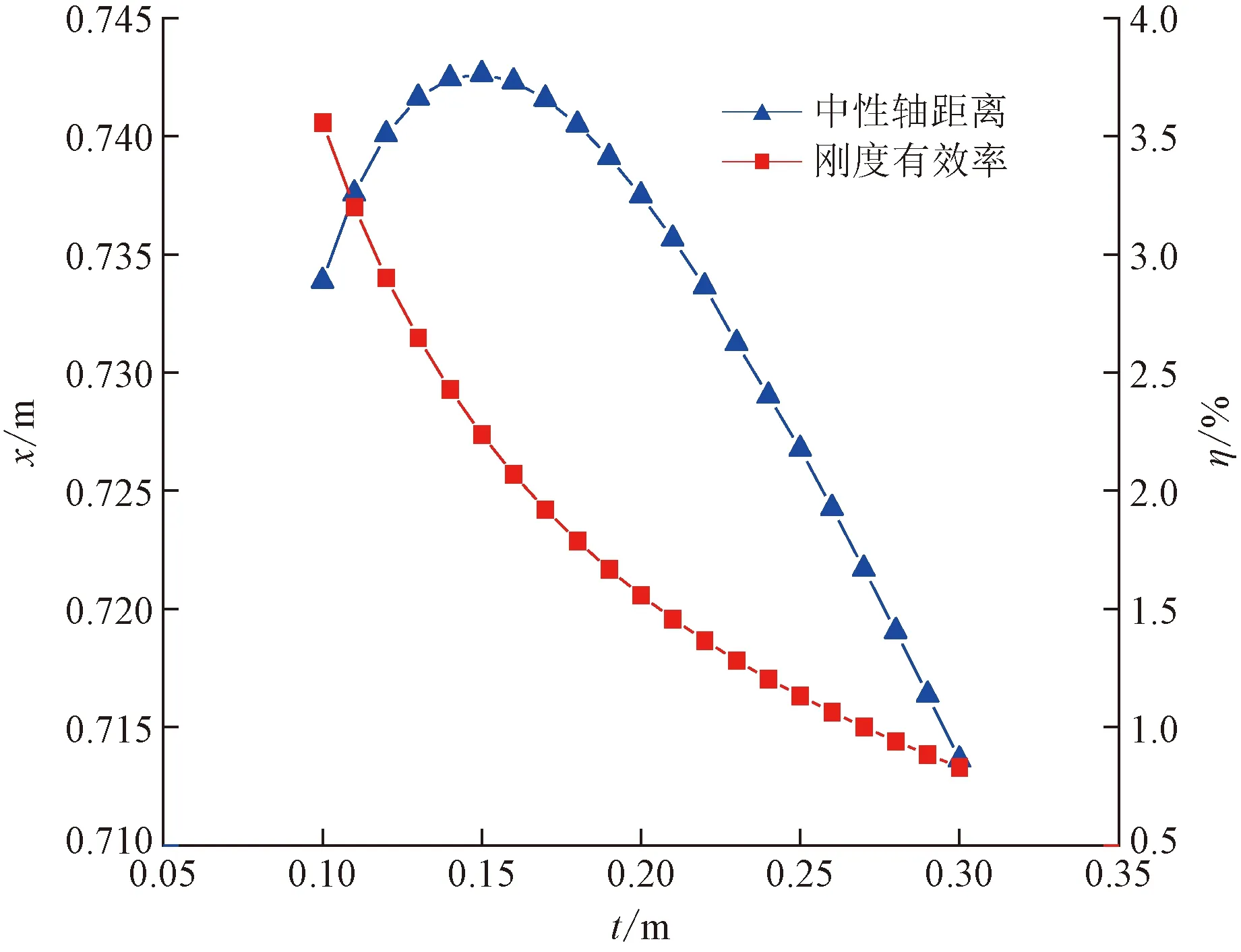
图7 刚度有效率及中性轴位置与管壁厚度之间关系

管壁厚度t由0.1 m增长到0.3 m时，刚度有效率η由3.558降至0.830，降低76.67%。管壁厚度t控制着管廊纵向等效抗弯刚度变化，但随着t的增加η降低幅度逐渐变小。通过增加管壁厚度可以提高管廊纵向等效刚度，但却降低了纵向等效抗弯刚度的有效率，说明欲提高管廊等效刚度，通过增加管壁厚度的方法有失经济性，故工程中应视情况合理设计管壁厚度。

3.3 管廊预制节段长度的影响

为研究管廊刚度有效率η和中性轴位置x受节段预制长度ls的影响程度和趋势，令节段预制长度从0.5 m增长到2.5 m，而其他参数保持不变，求出所对应的x和η，绘制变化曲线，如图8所示。

由图8可知，中性轴位置x随管廊节段长度ls的增加而减小。当ls由0.5 m增至2.5 m时，x由0.737 m降至0.567 m，降低23.07%。表明随着节段长度增加，中性轴愈发远离截面下缘，截面受压面积越大，受力状态越好。

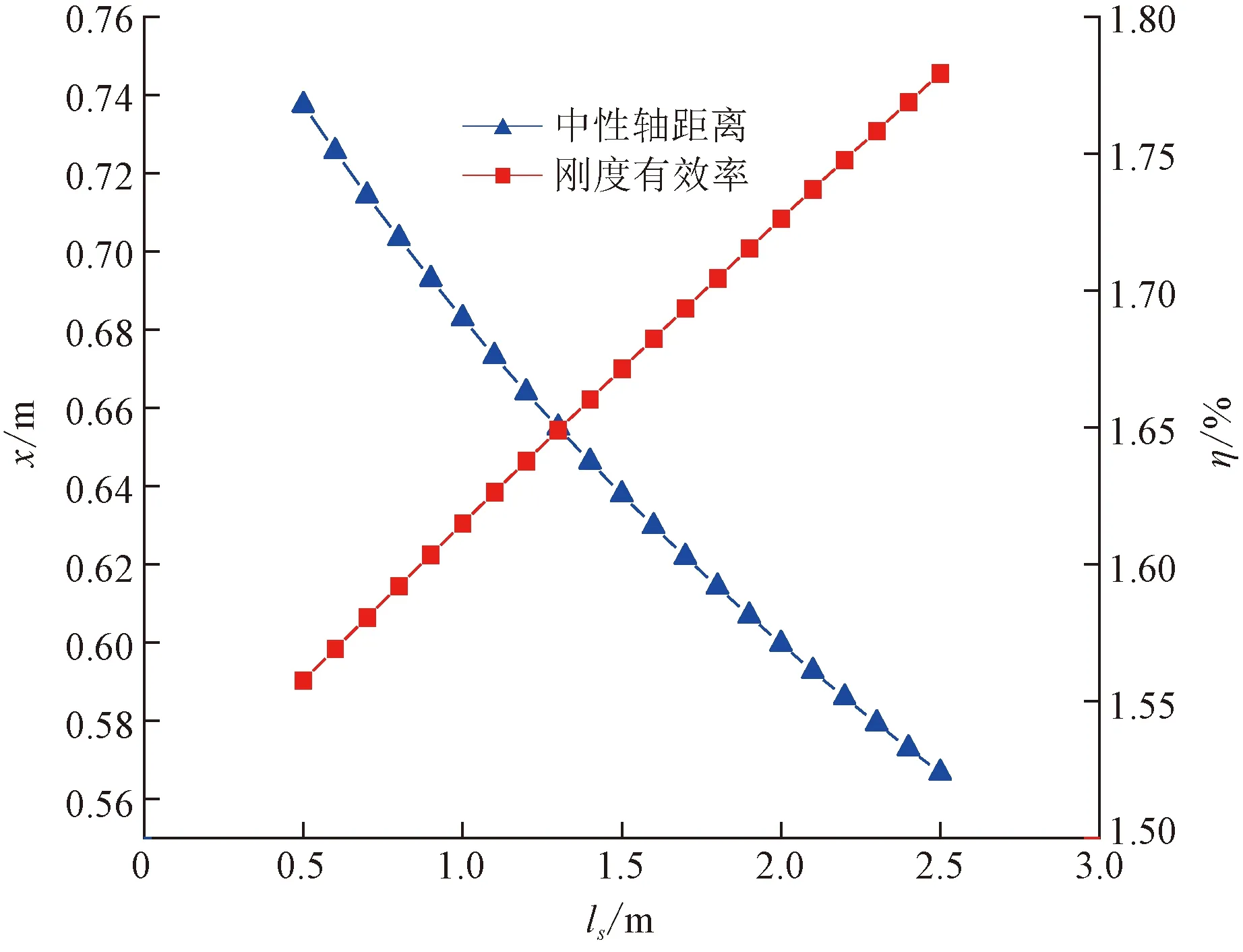
图8 刚度有效率及中性轴位置与节段长度之间关系

刚度有效率η随节段长度ls的增加而增加。当ls由0.5 m增长到2.5 m时，η由1.558增加到1.779，增长14.18%。由此可见，管廊的预制节段长度可以直接影响其刚度有效率的变化。表明，实际工程中，在满足设计要求条件下，适当增大预制节段的长度，可以有效提高管廊的纵向刚度，并且能够很好地改善管廊截面受力状态，同时不失经济性。

3.4 螺栓数量的影响

为研究刚度有效率η和中性轴位置x受接头螺栓数量n的影响，固定其他参数不变，令单个接头的螺栓数目n从8个以4个逐次增加至36个，以刚度有效率η和中性轴位置x为因变量，绘制变化曲线，如图9所示。

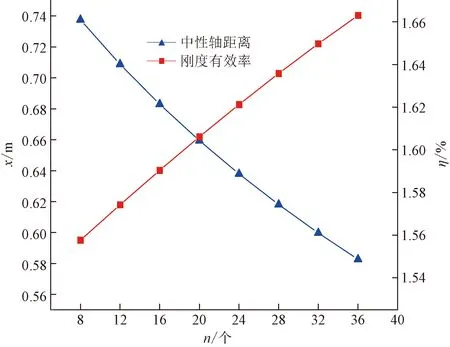
图9 刚度有效率及中性轴位置与螺栓个数之间关系

由图9可知，中性轴位置x随螺栓数量n增加而减小。当n由8增至36时，x由0.737 m降至0.583 m，降低20.89%。与管廊节段长度增加相同，随着螺栓数量增加，中性轴愈发远离截面下缘，截面受压面积越大，受力状态越好。

当螺栓数量n由8增长到36时，刚度有效率η由1.558增至1.663，增长6.73%。与管廊节段长度增加相似，螺栓数量也是直接影响刚度有效率的主要因素，但其影响程度较节段长度因素要逊色一些。表明，实际工程中，在满足设计要求条件下，适当增加螺栓数量，可以有效提高管廊的纵向刚度，且能够很好地改善管廊截面受力状态。