基于膝点驱动进化算法的工程施工多目标优化

刘澍， 王军武

(武汉理工大学土木工程与建筑学院， 武汉 430070)

缩短工期、降低成本是所有工程施工管理人员共同追求的目标。中国建筑业在经济水平不断提高和社会高速前进的时代背景下蓬勃发展，建设项目的大型化、复杂化和系统化程度不断提高，已有的工期-成本优化已无法满足建筑业接续发展的实际需求。建筑业作为危险系数较高的行业，人身财产事故发生率在各行业中居高不下，建筑业的健康持续发展需要重点关注安全目标。建筑业作为国民经济的支柱行业之一，深刻影响着环境，结合中国大力提倡节能减排的大时代背景，对生态环境影响巨大的建筑业需要做出应有的表率作用，因此施工过程的环境影响也是一大需要关注的目标，需要在满足其他施工目标的前提下尽可能减少环境影响。

现以工程项目施工过程为研究对象，以工期-成本-安全-环境为目标，构建施工多目标优化体系，以期为施工管理者权衡各施工目标和施工计划的制定提供一定的指导和借鉴。

1 施工多目标优化问题

1.1 工期-成本优化问题

多目标优化在工程施工领域的应用起始于工期-成本问题,目前存在广泛研究。针对工程成本优化和工期风险分析问题。 He等[1]基于量子遗传算法建立了工期和成本最小的多约束多目标结构优化模型。马宁[2]构建基于遗传算法的工程项目多目标调度模型，为进度最优和成本最小化的权衡提供理论参考。杜镀等[3]运用遗传神经网络和免疫粒子群算法的组合方法以求解工序复杂的地铁隧道施工工期-成本优化问题。王绪民等[4]结合改进的非支配排序遗传算法Ⅱ(non-dominated sorting genetic algorithm-Ⅱ，NSGA-Ⅱ)算法与建筑信息模型(building information modeling，BIM)5D模型，考虑生产效率，对工期-成本多目标优化模型进行了改进。傅刚辉[5]采用BIM技术结合遗传算法对建设项目的工期和成本进行优化分析，降低成本同时提高建设项目的整体质量。

从现有文献看，施工工期-成本优化问题的研究已经比较成熟，典型的智能算法如蚁群算法、粒子群算法、遗传算法等都能有效地解决这类优化问题。但是考虑质量、安全等额外目标时，该类方法的效用相对有限。

1.2 引入其他目标的施工多目标优化问题

随着施工多目标优化问题的研究进一步深化，越来越多的学者开始引入新的施工目标。杜学美等[6]采用粒子群算法将工期、成本、质量和安全结合起来，以项目的施工方案为决策变量，建立了施工多目标优化模型。Li等[7]将质量-成本-工期-安全作为一个系统，建立多目标优化模型，采用改进蚁群算法对建设项目进行多目标寻优。Yang[8]以建设项目的工期、成本和质量为优化对象，提出了一种基于多蚁群算法的建筑项目多目标优化方法。谢存仁等[9]以工期-成本-资源为目标，构建BIM-遗传算法施工优化模型，加强BIM技术和施工过程优化的结合水平。Dong等[10]将遗传算法融入BIM平台，引入虚拟施工、碰撞检查等方法，提出了工期、质量、安全和成本之间的多目标优化设计。

已有学者将工期-成本-安全-质量目标综合考虑，采用多目标粒子群算法和遗传算法等方法求解，通常求解的是三目标问题，当求解4个以上目标时采用固定其中一个目标为约束的方法，且大多只使用工期一个自变量，无法全面体现施工各目标间的联系。已有方法求解众目标(3个及以上目标)施工优化问题，获得最优解集时存在瓶颈，包括：搜寻过程耗时长；指标计算较复杂，难以搜寻邻近解；算子不具备足够的搜寻性能[11]。现拟采用在众目标优化中具有较优性能的膝点驱动进化算法(knee point driven evolutionary algorithm，KnEA)求解工程项目施工工期-成本-安全-环境多目标优化问题，同时创造性地考虑工期和成本为自变量输入，以期为工程施工众目标优化提供一种可供参考的有效途径。

2 基于KnEA算法的施工工期-成本-安全-环境优化模型

2.1 工期目标函数

在不同的施工组织模式下，由于人工、材料、机械设备、施工方案等方面的差异，工程的每一道工序的工序时长也会有所不同。项目总工期由工程项目网络计划中关键线路上各工序工期求和得来，关键线路是网络计划中完全由关键工序连成的线路，关键工序的总时差为0。根据关键线路原理，构建的工期目标函数为

f(1)=minT

(1)

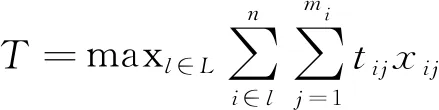
(2)

式中：T为建设项目总工期；i为施工工序；n为项目施工总工序数；j为施工组织方式；mi为施工工序i有m种施工组织方式；L为项目网络图中所有线路的合集；l为项目网络图中的关键线路；i∈l为由关键线路组成的施工工序集合；tij为施工工序i采用第j种施工组织方式时的持续时间；xij为索引变量，当xij=1时，表示第i项施工工序执行第j种组织方式，当xij=0时，表示第i项施工工序不执行第j种组织方式。

约束条件如下。

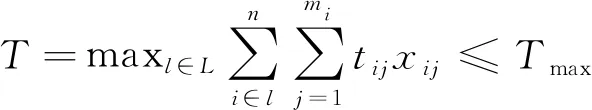
(3)

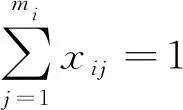
(4)

式中：Tmax为项目所能接受的最大工期。

2.2 成本目标函数

建设项目的总成本包含从项目开始到项目竣工交付的整个施工过程中产生的直接成本和间接成本的总和。构建成本目标函数如下。

f(2)=minC

(5)

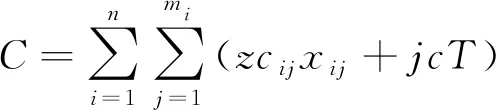
(6)

式中:C为建设项目总成本；zcij为采用j项施工组织方式时第i项施工工序的直接成本；jc为项目的间接成本费率。

约束条件如下。

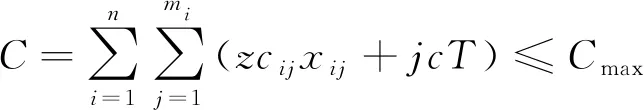
(7)

式(7)中：Cmax为项目所能承受的最高成本。

2.3 安全目标函数

工期和成本都会对工程项目的安全水平造成影响，相关学者对于量化工期-安全、成本-安全的函数关系进行了深入的研究，在综合考虑已有研究成果后，采用如下概念构建安全目标函数。

(1)工期与安全水平为非线性关系，存在使得项目安全水平最高的工期。在最佳工期之前，工期越长，保障安全的时间越多，产生安全事故的可能性越小，安全水平越高，随着安全工作的投入，继续延长工期带来的安全水平提高的显著性有限，逐渐趋于稳定。但超过最优工期后，工期过长，施工人员会产生倦怠情绪，露天堆放的部分施工材料或工具也增大了被破坏的概率，使得安全水平不升反降。

(2)成本从两方面对安全水平产生影响，即保障性安全成本与损失性安全成本。保障性安全成本是为确保施工安全而投入的安全费用，是项目总成本的一部分；损失性安全成本也称为事故成本，是指发生安全事故后，拿来处理事故产生的后果所需的费用。损失性安全成本无法在决策阶段进行决断，所建立的工期-成本模型考虑的是保障性安全成本与安全水平之间的关系，保障性安全成本与施工安全水平的关系为，随着保障性安全成本的增加，施工安全水平会相应提高，但上升到一定程度后会保持基本不变，因为安全风险是无法完全根除的。

建立的工期-安全水平函数关系如下。

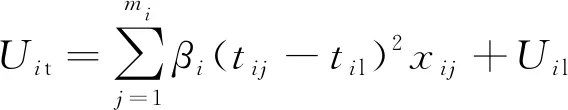
(8)

LUit=1-Uit

(9)

式中：Uit为工期影响工序i的安全风险；βi为工期安全相关系数；LUit为工期影响的工序i的安全水平；Uil为工序i最低安全风险；til为工序i最长持续时间；tij为工序i在j组织方式的持续时间。

约束条件如下。

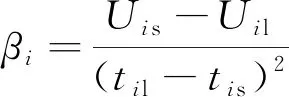
(10)

tis≤tij≤til

(11)

0≤Uit≤1

(12)

0≤LUit≤1

(13)

式中：Uis为工序i最高安全风险；tis为工序i最短持续时间。

成本-安全水平函数关系如下。

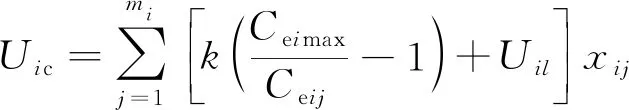
(14)

LUic=1-Uic

(15)

式中：Uic为成本影响的工序i的安全风险；LUic为成本影响的工序i的安全水平；Ceij为工序i在j组织方式的保障性安全成本(Ceij=2%Cij)；k为保障性安全成本与安全风险相关系数。

约束条件为

0≤Uic≤1

(16)

0≤LUic≤1

(17)

工序的工期、成本-安全水平函数关系为

LUi=φLUit+(1-φ)LUic

(18)

式(18)中：φ为工期对安全影响的权重系数。

依据网络系统可靠性理论，项目总安全水平与各工序安全水平的关系为

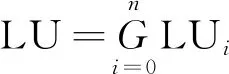
(19)

式(19)中：LU为工程项目安全水平；LUi为工序i的安全水平；G为网络系统可靠性模型。

工序i的安全水平网络输出值为

(20)

对于整体项目，安全水平目标函数为

f(3)=maxLU

(21)

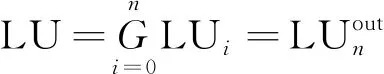
(22)

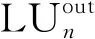
约束条件为

0≤LUi≤1

(23)

LU≥LUmin

(24)

式中：LUmin为项目需达到的最低安全水平。

2.4 环境目标函数

在苏贵良[12]构建的考虑工程项目对环境直接影响和间接影响的工期、成本-环境影响目标函数基础上进行改进，构建如下环境目标函数关系。

f(4)=minE

(25)

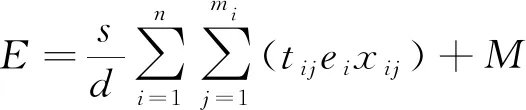
(26)

(27)

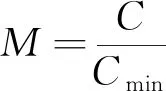
(28)

式中：E为项目对环境的总影响值；d为项目与居住区直线距离；s为项目所在城市的经济水平指数，以华中地区某城市为参照；ei为工序i对周围环境的污染和破坏程度；M为项目能源和资源消耗对环境的影响值；Cmin为项目最低成本；np为城市人口数量；GDP为城市生产总值(gross domestic product)。

约束条件为

E≤Emax

(29)

式(29)中：Emax为项目可接受的最高环境影响。

2.5 工期-成本-安全-环境综合优化模型

同时考虑工期、成本、安全和环境目标，期望达到最小工期、成本和环境影响目标和最大安全目标，构建工程项目工期-成本-安全-环境多目标优化模型为

minF=min[f(1),f(2),-f(3),f(4)]

(30)

约束条件为

{式(3),式(4),式(7),式(10),式(11),式(12),式(13),式(16),式(17),式(23),式(24),式(29)}

(31)

3 求解多目标优化问题的KnEA算法

3.1 KnEA算法相关背景

膝点驱动进化算法KnEA是 Zhang等[13]学者于2015 年提出的一种新型多目标优化算法。该算法的核心是引入knee points(膝点)，膝点是帕累托前沿面上“最凹”的点，它对帕累托解集的贡献最大。现有的大多数多目标进化算法在高维多目标优化中性能不佳的主要原因之一是由于种群中的大多数解都是非支配解而缺乏选择压力。

当决策者缺乏有支配地位的决策偏好时，膝点可以使决策者更快地做出选择，从而提高算法的收敛性，在非支配解的前沿，最多将一个解视为其邻域内的膝点，因此无须引入额外的维护机制以保证种群多样性，降低了运算复杂度。

3.2 KnEA算法求解多目标优化问题的步骤

KnEA算法求解本文工程项目施工工期-成本-安全-环境多目标优化步骤如图1所示，具体如下。

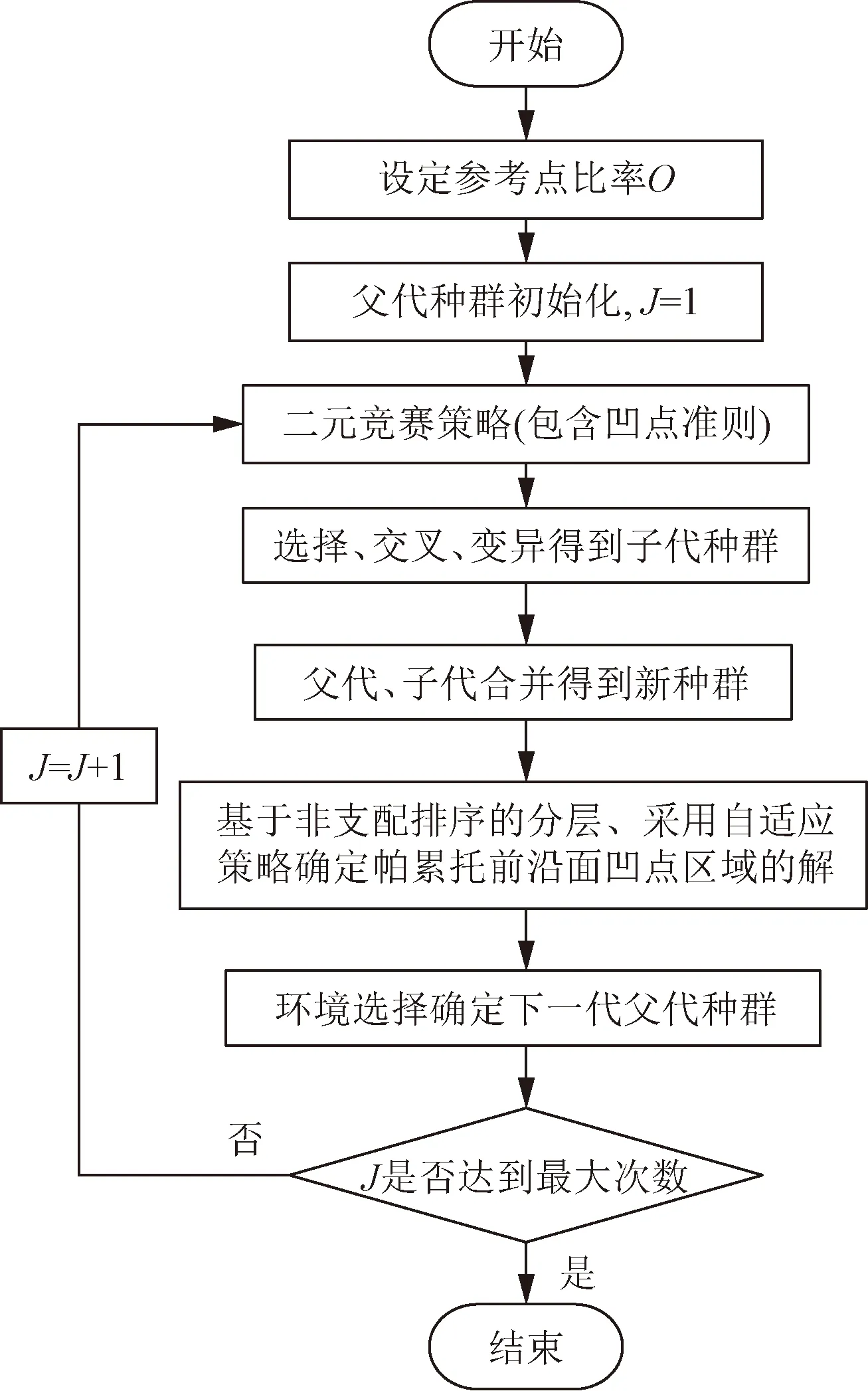
图1 KnEA算法多目标优化流程

步骤1初始种群Pt(规模为K)根据输入的优化目标数M和决策变量数N进行初始化，设定种群中膝点的比率O。

步骤2应用二元竞赛策略从亲本种群中选择个体，利用变异方法生成N个后代个体。在二元竞赛选择中，采用三种竞赛度量，即优势关系、膝关节点准则和加权距离度量。

步骤3对父代和子代组合进行非支配排序，然后采用自适应策略确定组合群体中每个非优势前端膝关节区域的解。

步骤4依靠环境选择筛选N个个体作为下一代的父代群体。

步骤5重复上述步骤，直到符合终止条件。输出此时的父代种群，得到优化后的施工多目标决策变量集合和解集。

4 工程项目施工工期-成本-安全-环境多目标优化案例

4.1 相关参数设置

案例项目为装配式工业厂房项目，由双鸭山程翔建筑安装有限责任公司承建。厂房包括三跨单层工业厂房，建筑面积7 482.5 m2，单跨跨度23 m，屋面标高21.8 m，室内标高0.00 m，室内外高度差0.15 m。该项目由12 项工序组成，分别为施工准备(A), 基础工程(B), 现场构件制作(C), 结构吊装工程(D), 屋面工程(E), 水磨石地面装饰(F), 门窗安装(G), 轻骨料钢筋砼板墙体安装(H), 内外墙装饰(I), 钢筋砼构件刷涂料(J), 油漆工程(K), 竣工收尾(L)。每道工序由3种施工组织方式，分别为紧急 (1)、正常(2)、宽松(3)。项目网络图如图2所示。

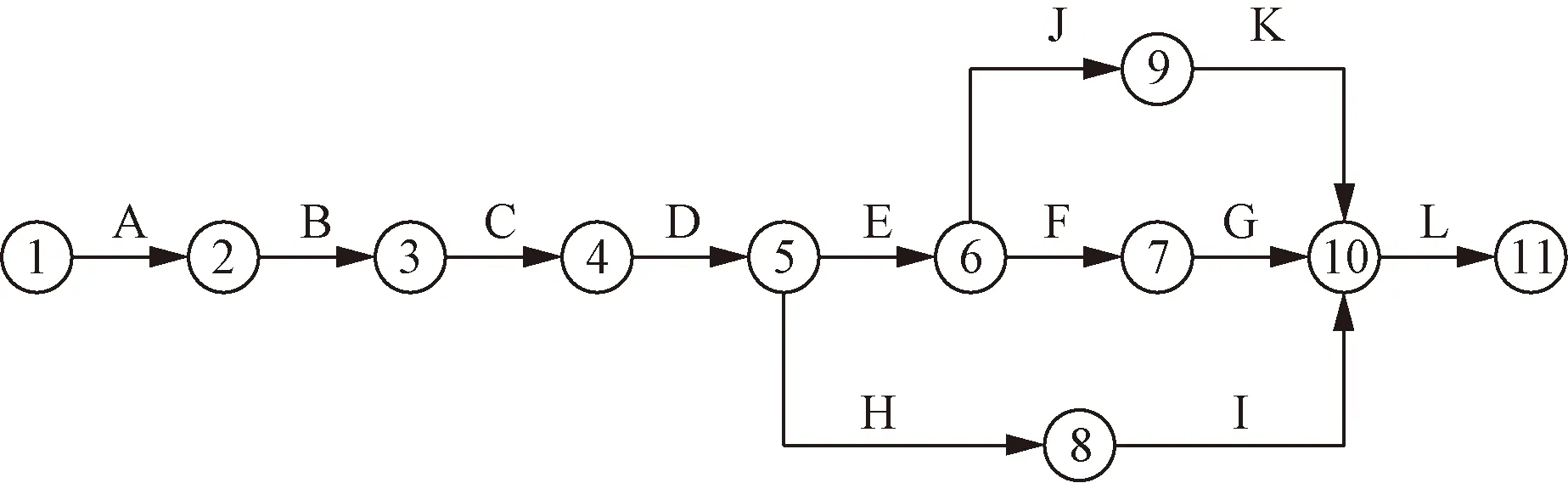
图2 装配式项目网络图

项目所在地为黑龙江省双鸭山市，2020 年人口数量120 .880 3 万人，GDP为493.9 亿元，项目距离最近的居民聚集区直线距离约为40 km。依据工程合同和国家相关标准的要求，项目总成本不超过2 151万元，总工期不超过234 d，工程安全水平不低于0.85，环境影响指数不超过3，本项目间接成本率为3 454 元/d。项目各工序相关参数如表1所示，其中，各工序在不同组织方式下的工期、直接成本依据施工组织设计和工程合同核算得到；Uil、Uis根据各工序安全风险控制的难度和以往同类工程的工序事故发生概率，通过专家打分法和查阅文献得出；ei综合考虑多项环境影响因素，由专家对各工序各影响因素的环境影响打分赋权求和得来；φ经过查阅资料和征询专家意见后赋值0.42，k依据已有学者的实验经验赋值0.089[14]。

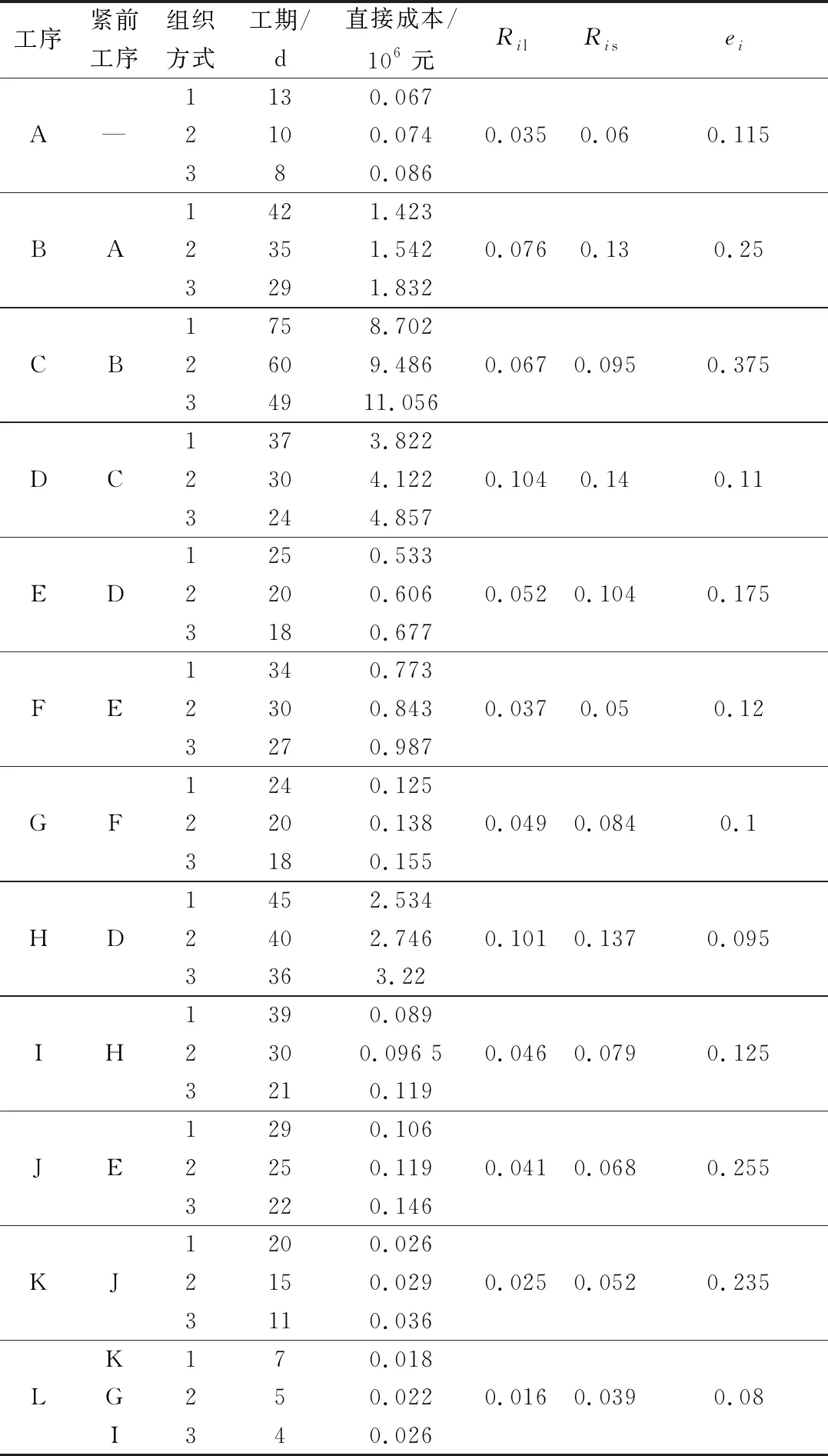
表1 项目各工序相关参数

4.2 案例求解过程

使用基于MATLAB的多目标进化算法实验平台PlatEMO[15]进行实验操作。优化模型以工序i的施工组织方式j为设计决策变量，以实数编码方式编码，变量的上下限为[1 3.999 99]。

步骤1编写目标函数及约束函数。将各目标函数以MATLAB代码的形式编写，分别单独存储，命名为F1，F2，F3，F4；约束函数同理存储为cons1，cons2，cons3，cons4。

步骤2导入项目相关数据。项目各工序的施工组织方式、工期、成本、风险系数等相关实验参数，由Excel表格导入，由下列代码读取数据：

[num,txt,raw] = xlsread(…)。

步骤3通过以下代码设置算法参数。

LB = ones(n,1);

UB = 4*ones(n,1) - 0.000 01;

[Dec,Obj,Con]=platemo(′objFcn′,{@F1,@F2,@F3,@F4},′conFcn′,{@cons1,@cons2,@cons3,@cons4},′lower′,LB′,′upper′,UB′,′algorithm′,@KnEA,′N′,300);

Dec = floor(Dec);

其中种群数量300为根据以往实验经验以及实测合理性后确定的参数。

步骤4运行程序，实现优化过程。

4.3 案例优化结果分析

(1)最优解集合。真实Pareto前沿如图3所示，最终得到300 组Pareto最优解集组合，部分最优解集合如图4所示，最优解集合与对应工序施工组织方式如表2所示。

图3 真实帕累托前沿

图4 KnEA算法所求得的非支配解集合

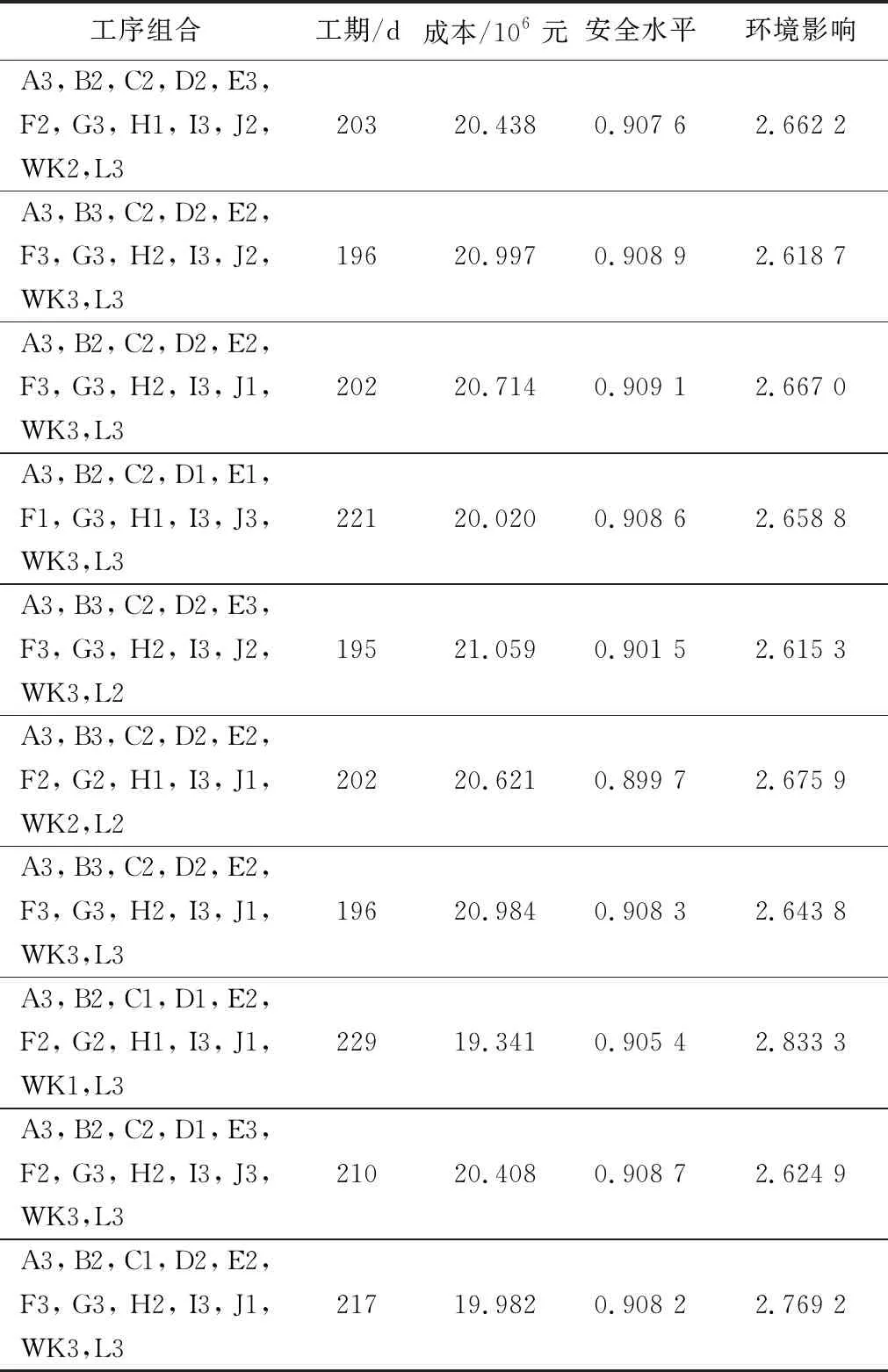
表2 最优解集与对应工序组织方式

(2)多目标间相关性分析。非支配解集在工期-成本-安全三维空间上的分布如图5所示，在工期-成本-环境三维空间上的分布如图6所示。可见随着工期的延长和成本的提升，项目的安全水平呈现上升趋势，随着工期的延长和成本的减少，项目对于环境的影响呈现上升趋势。

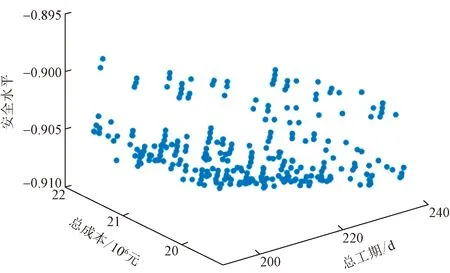
图5 工期-成本-安全目标三维图

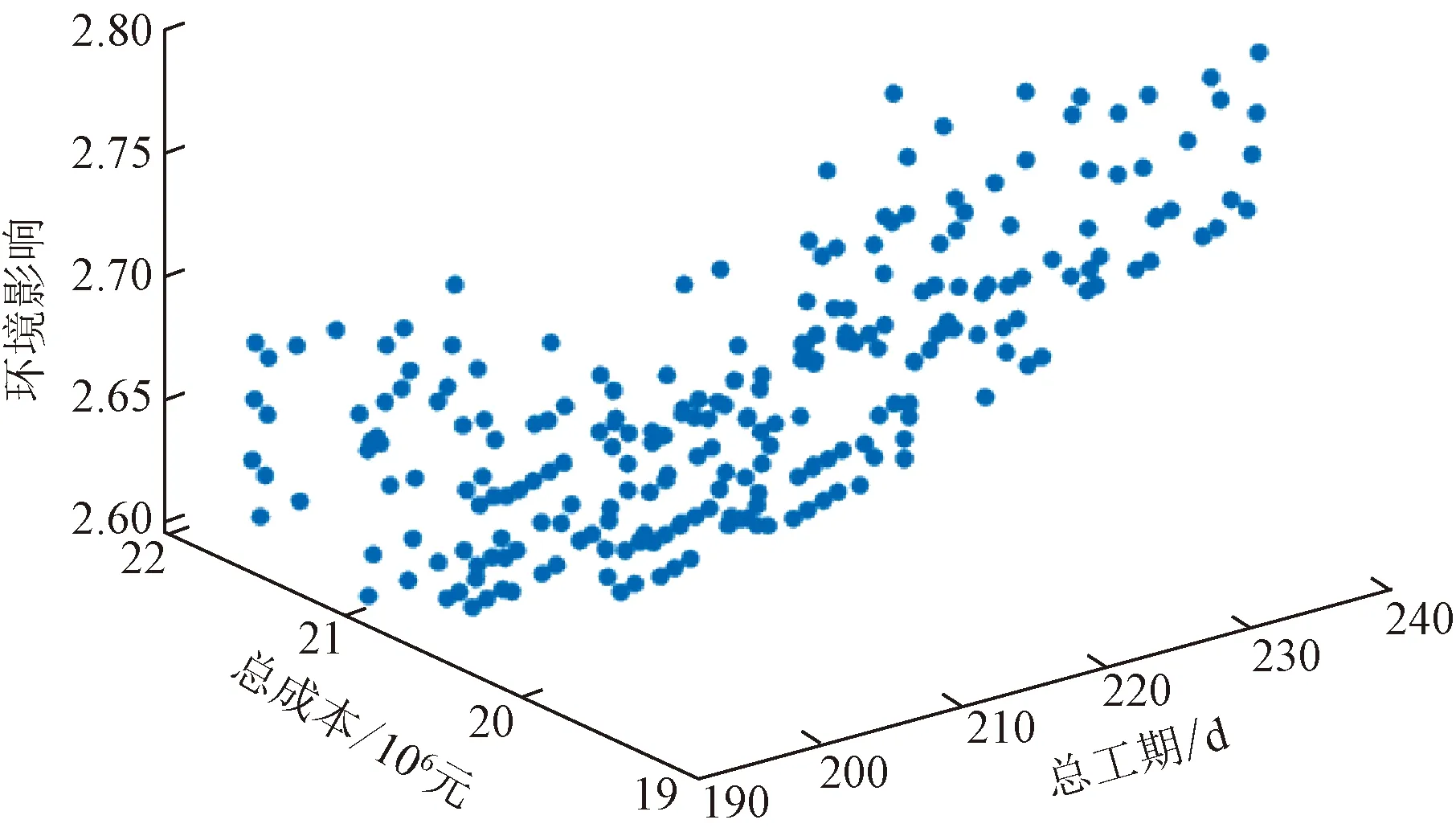
图6 工期-成本-环境目标三维图

(3)算法性能分析。采用多目标优化领域常用的多目标粒子群优化(multi-objective particle swarm optimization，MOPSO)、非支配排序遗传算法Ⅲ(non-dominated sorting genetic algorithm-Ⅲ，NSGA-Ⅲ)和参考向量引导进化算法(reference vector guided evolutionary algorithm，RVEA)作为对比算法，以超体积(hypervolume，HV)[16]为算法性能评价指标，分析KnEA算法用于工程项目施工多目标优化的使用效果。

各算法均设定群体数量为300，应用于工程项目施工多目标优化模型实验 (50 次实验取平均值)，KnEA、MOPSO、NSGA-Ⅲ和RVEA算法求得的解集数量依次为300、300、286和108；KnEA、MOPSO、NSGA-Ⅲ和RVEA得到的HV指标如图7所示，各算法HV依次为0.016 163、0.014 008、0.014 816和0.013 858，可见KnEA算法在工程项目施工多目标优化模型中具有较好的性能。

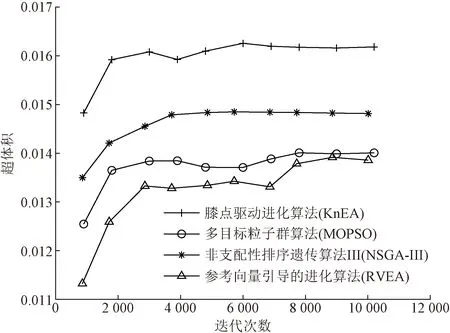
图7 算法 HV值对比

5 结语

工程项目施工多目标优化是近年来学者投入研究较多的领域，装配式建筑作为一种新型建筑形式，减少了现场施工人员的需求和施工废弃物的排放，具有更高的安全水平和更小的环境影响。以装配式建筑项目为实验案例，构建施工工期-成本-安全-环境多目标优化模型，经实验总结得出如下结论。

(1)研究具有可行性和实用性。在以往研究的基础上同时考虑工期、成本两大因素对安全水平的影响，改进环境目标函数，采用KnEA算法进行优化求解，得到300 组Pareto最优工工序组合，与典型多目标优化算法MOPSO、RVEA和NSGA-Ⅲ进行对比，验证了KnEA算法用于所构建工程项目施工多目标优化模型的优良性能。

(2)研究还存在不足。对于环境目标没有与成本因素建立有效的函数关系，目前的研究成果展现的环境-成本关系主要依托于工期对于成本变动的影响，后续需要进一步研究。