基于Softmax函数增强卷积神经网络-双向长短期记忆网络框架的交通拥堵预测算法
2022-11-16陈悦杨柳李帅刘恒唐优华郑佳雯
陈悦, 杨柳*, 李帅, 刘恒, 唐优华, 郑佳雯
(1.西南交通大学信息科学与技术学院, 成都 611756; 2. 综合交通大数据应用技术国家工程实验室, 成都 611756; 3. 西南交通大学唐山研究院, 唐山 063002; 4. 西南交通大学交通运输与物流学院, 成都 611756; 5. 西南交通大学计算机与人工智能学院, 成都 611756)
在朝着中国建设现代化城市而努力发展的目标指导下,经济不断增长,城市居民对出行服务需求不断提高,机动车总数不断增长。而由这些因素带来的交通拥堵已经逐渐开始发展并成为一个社会重大问题,对城市的可持续发展造成了严重的威胁。
当交通拥堵时,汽车运行缓慢,出行时间也不断增加,导致严重的能源浪费。目前为止中国的机动车年均数量增长率一直在快速不断上升,现在已经快速发展成为世界第二。由于汽车尾气大量排放而严重导致的城市空气污染日益严重。为了有效减少交通拥堵带来的严重生态环境污染,有必要科学地防治交通拥堵,让市民避开拥堵地区,绕行拥堵地区,降低出行时间。智慧交通系统(intelligent traffic system,ITS)的建设为城市发展提供了新的支撑点,如全球定位系统(global positioning system,GPS)、车联网、路网监控、地图导航等技术的应用产生了拍字节(Petabytes,PB)级的交通数据。如何从这些海量交通数据中挖掘出高价值信息,总结分析出相应规律,使之有效地改善交通状况、提高交通管理水平,已成为一个迫切需要解决的问题。
近几年数据挖掘技术的发展则为处理这些海量交通数据提供了新的可能性。从这些海量交通数据中挖掘出来的有用信息,用于分配交通资源,将会解决交通拥堵问题。因此,这一领域的研究具有重要意义。
在交通拥堵预测问题上,学者们已经做了大量的研究工作,一般分为3类方法。
(1) 基于统计学理论的预测方法。Ahmed等[1]首次提出应用自回归移动平均模型(autoregressive integrated moving average model,ARIMA)预测短时交通流,取得了较为满意的结果。自回归移动平均模型(ARIMA)开始被广泛应用于分析带有时间序列的交通现象的变化规律,尤其在交通预测领域受到国内外诸多学者的青睐。唐毅等[2]通过优化样本序列的动态选取和模型识别,提出了一种改进的时间序列模型,对高速公路上的交通流量进行短时预测。蔡昌俊等[3]基于城市轨道交通自动售票系统采集的地铁站进出站历史客流数据,利用ARIMA模型对广州地铁进出站客流进行了预测。
(2) 基于神经网络的预测方法。Park等[4]在前人对于神经网络算法研究的基础上,使用相同的数据集对比了反向传播(back propagation,BP)神经网络和径向基函数(radical basis function,RBF)神经网络,对比两种方法进行短时交通流预测,证明了径向基神经网络复杂度较小且准确率更高。户佐安等[5]基于BP神经网络的交通信息量预测模型,并通过因子分析和因子分析结果归一化处理减少了BP神经网络输入数据规模,缩短了神经网络预测时间。Wang等[6]提出了一种基于卷积神经网络(convolutional neural networks,CNN)的错误反馈递归神经网络用于预测连续交通速度。在基于CNN的方法中,可以利用时间和空间维度信息构造时空矩阵。Xu 等[7]提出了一种新的图神经网络的变种,即时空变压器网络。该网络利用动态定向空间依赖和长期时间依赖来提高长期交通预测的准确性,通过动态建模定向空间依赖与自注意机制,以捕获实时交通状况和交通流的方向性。
(3) 基于多模型融合的方法。 Xu等[8]使用基于CNN和长短期记忆(long short-term memory,LSTM)以共同捕获道路网络上空间和时间依赖性。通过CNN提取空间特征,LSTM提取时间特征,还考虑了一些外部因素,可以一步提高预测准确性,通过北京交通数据集的实验测试证明了该方法的优越性。刘振辉[9]通过XGBoost模型与LightGBM两种算法进行训练加权融合进行交通预测,通过实验仿真验证该方法能够准确地进行道路交通流量的实时预测。宋瑞容等[10]为了精准预测交通流量,充分提取交通流中复杂的线性和非线性特征及其依赖关系,提出了融合多维时空特征的CLABEK模型。由Conv-LSTM、BiLSTM和Dense神经网络分别提取时空特征、周期特征和额外特征。牟振华等[11]提出一种小波降噪与贝叶斯神经网络联合模型的预测方式,引入平均绝对百分比误差和标准误差作为模型评价指标,从精度和稳定性两个方面对模型进行评价。Zhang等[12]提出了一种基于深度学习的方法,称之为时空残差网络ST-ResNet,来同时预测城市中每个区域的流入和流出客流量。通过使用残差神经网络框架来对拥堵流的时间临近性、周期和趋势特性建模。李兆丰[13]等以LSTM神经网络为基础预测框架,构建融合多特征的“端到端”短时客流预测框架,挖掘客流的时间依赖性特征,通过Embedding层嵌入外部因子稀疏矩阵,再利用全连接层融合时间特征、空间特征和其他因子得到预测结果。
通过对研究现状以及目前各种预测方法的优劣性分析。因此,现拟采用多模型融合的方式来进行预测,提出一种基于CNN和双向长短期记忆(bidirectional long short-term memory,BiLSTM),并结合Softmax函数的CS-BiLSTM预测框架。
对比传统神经网络模型在旅行时间指数(travel time index,TTI)拥堵预测上的效果,验证LSTM网络结构在时序数据预测上的优越性,然而在预测TTI系数的空间相关性上仍存在不足。因此现将城市拥堵状态的网格区域作为一个图像来学习,并结合CNN与BiLSTM,采用C-BiLSTM的交通预测框架,并进行预测实验,对比实验结果证明该交通预测模型在TTI系数上的预测准确度与传统的两种神经网络模型的准确度。随后对该预测模型进行改进,提出CS-BiLSTM预测框架,验证新的框架在拥堵预测上的准确性。
1 交通状态概述
为了解决交通拥堵问题,需要对交通状态进行识别。对于交通状态的认知,人们经常使用分类的方法来区分状态,比如将其划分为畅通、拥堵等级别。交通状态表现为具有随机、随时间变化、空间相对等物理特征的现象,反映了道路交通流的全局运行表现。
在微观层面,交通状态可以量化为车辆的速度、交通量、队列长度、延迟长度等指标。而在中观层面,人们使用了正常的状态或者异常的状态去表现和描述各种交通工具的运行状态。正常的状态即路网能够正常承载交通出行需求。异常的状态一般表现在道路上有可能发生了交通拥堵或者出现了交通事故,使车辆不能正常行驶。从宏观上看,交通状态表示为路网的平滑度,可以用不同拥堵程度的交通事故数、道路里程[14]等指标来描述。
交通状态是一个主观特征较强的概念,各国对交通状态的衡量标准还不统一。在决策者之间的差异层面上,不同的交通决策者对交通状态有不同的理解。即使是同一个决策者,在不同的时间和情绪下,对同一路段的交通状况也会有不同的感知。对于交通状态的认知,交通管理者应根据区域内交通流的特点进行思考。
交通流预测模型主要是基于对采集的历史交通数据以及实时的交通流数据进行深度地挖掘和分析后,来预测未来交通流发生情况的数学模型[15]。一般将预测时长小于15 min的交通流预测称为短时交通流预测。对于短时交通流量的可预测性,贺国光等[16]进行了较为深入的研究,他们得出了采样间隔为5~15 min的短期交通流是可预测的。
对于交通流预测模型,常用以下3个评价指标对模型进行评估。
(1)均方误差。
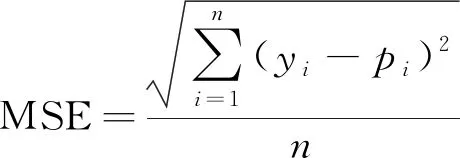
(1)
(2)平均绝对误差。
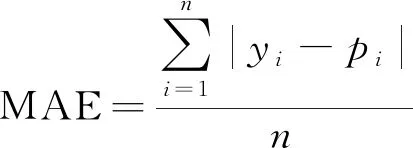
(2)
(3)平均绝对百分比误差。
(3)
式中:yi为真实值;pi为预测结果。
主要采用MSE和MAE这两个指标对模型预测结果进行评价。
2 基于城市网格区域的交通拥堵指标分析
2.1 基于出行时间指数的交通拥堵指标
旅行时间指数(travel time index,TTI)是衡量城市拥堵程度的一项指标。它所反映的是实际出行花费的时间和以自由流速度为期望速度出行所花费的时间的比率。它具有以下特性。
(1)可以非常全面、方便了解城市实际交通状况。
(2) 由于不同城市的交通情况存在差异,指标TTI只需根据路网长度来分配每条道路的加权参数。
(3) 易于交通管理部门和研究机构进行探索规律,研究特征,且方便大众使用。
TTI的计算公式为
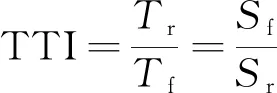
(4)
式(4)中:Tr为实际的平均旅行时间;Tf为以自由流速度为期望的旅行时间;Sf为道路的自由流速度;Sr为实际旅行速度。
2.1.1 自由流速度
自由流速度指路段在交通运输量较低、车流密度较低的情况下机动车所能达到的通过速度。其计算方法如下。
步骤1收集在一段时间内的旅行速度数据。通过一个路段长度,在一天 24 h的时间内,以间隔不超过15 min为一个时间段(如果时间间隔中轨迹的数量没有达到一定的阈值,则输出null,这是一个无效的样本),连续检测一个月。
步骤2将每个时间间隔的观测期内的所有有效样本的行驶速度进行算术平均。如果有效样本未达到某一阈值,则该时间间隔的移动速度不计入后续计算。
步骤3以4 h为一个基础时间样本,根据单个样本中的最大平均作为该路段的自由流速度。
2.1.2 权重计算
根据每条路段的类型和长度,在总路段长度中所占比例来确定各路段的权重系数,计算公式为
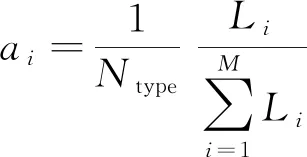
(5)
式(5)中:i为每段条路段的编号;Li为该路段的长度;Ntype为道路类型的总数;M为路段总数。
2.1.3 区域TTI计算
求得每条路段的权重后,就可以将每条路段的TTI值加权平均,得到区域内的TTI,这就可以反映出当前区域内的拥堵情况,计算式为
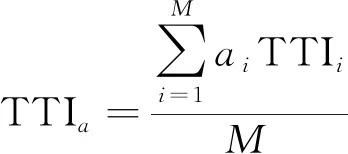
(6)
式(6)中:TTIi为路段的TTI系数。
计算得出的TTI越大,说明该区域交通运行状态越差。因此可以得出TTI与区域的拥堵程度具有正相关。
2.2 网格区域TTI的计算
一个城市的交通状态是城市中各部分交通状态的总和。因此,将整个城市区域根据经纬度切分成7×7的网格矩阵,然后识别各个地理区块中的交通状态,最后综合所有的地理区块的拥堵状态来反映城市一个整体的交通状态。再把每15 min构建的7×7网格矩阵作为输入。
将某市地理区块的切分并编号,如图1所示。区域的划分可以根据不同的需求来进行放大或者缩小,对应不同的地区级别。
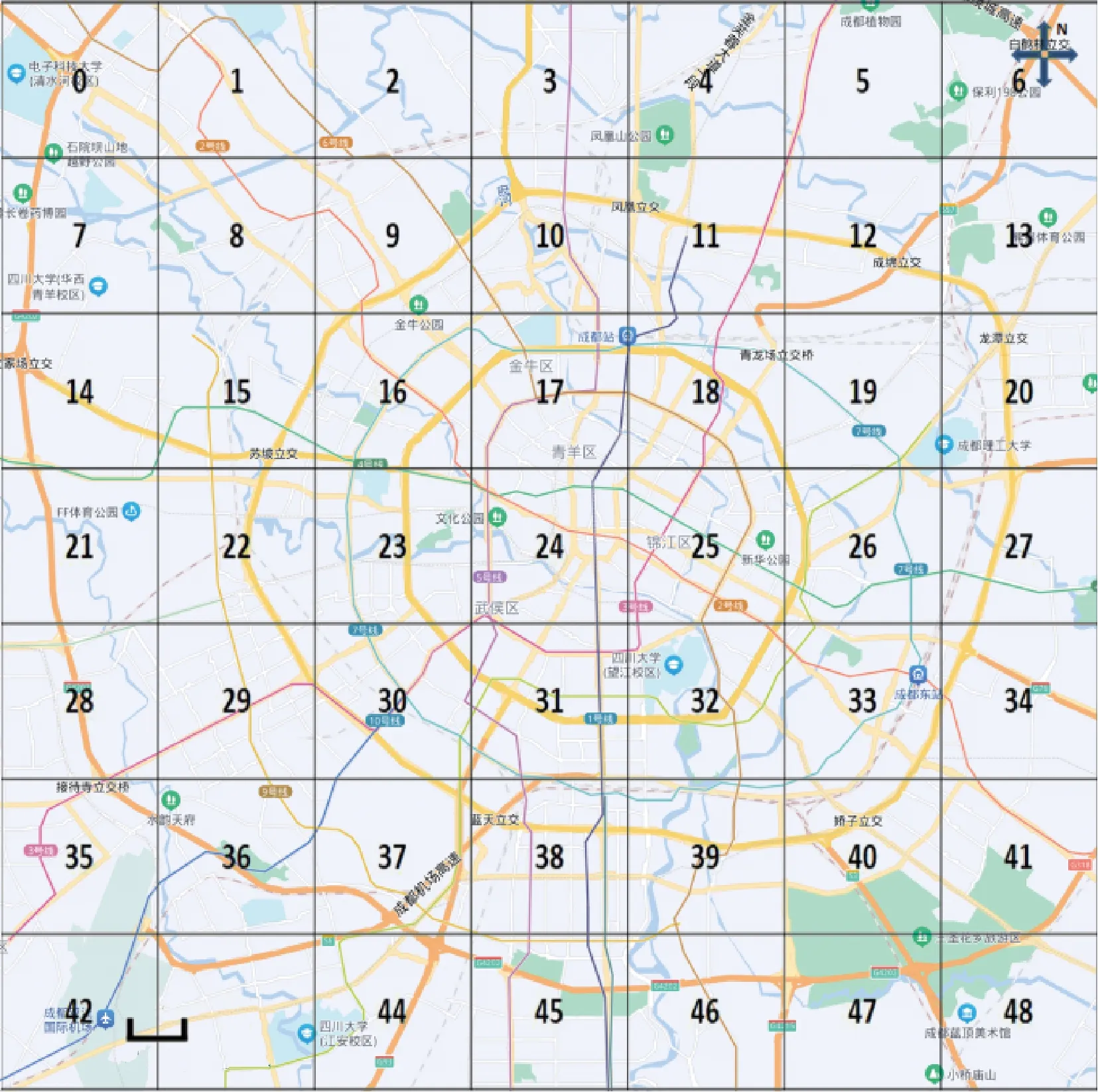
图1 某市地理区域划分
经过计算,2018年3月5日9:00每个区域的TTI如表1所示。
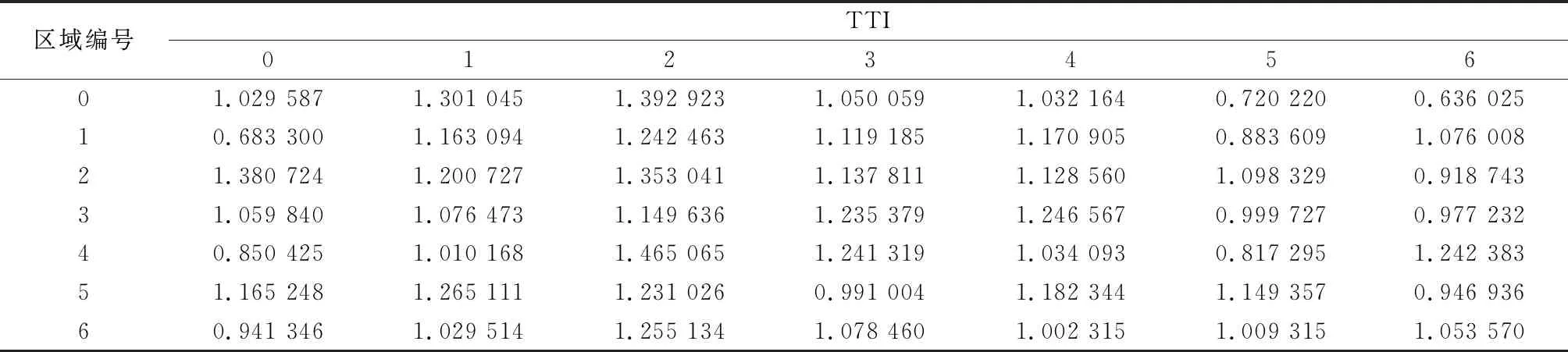
表1 市区TTI拥堵系数表(2018-03-05-9:00)
2.3 区域交通拥堵判别
根据道路平均车速与道路流量关系图,如图2所示。在道路平均车速大于自由流速度时,道路流量并未达到最大流量,此时路网不会出现拥堵情况。当道路平均车速小于自由流速度时,此时道路流量开始下降,出现拥堵现象,此时TTI=1。当TTI>1时,道路就处于拥堵状态。因此,定义TTI<1为畅通,TTI≥1为轻微拥堵,TTI>1.2为中度拥堵,TTI>1.5为严重拥堵。
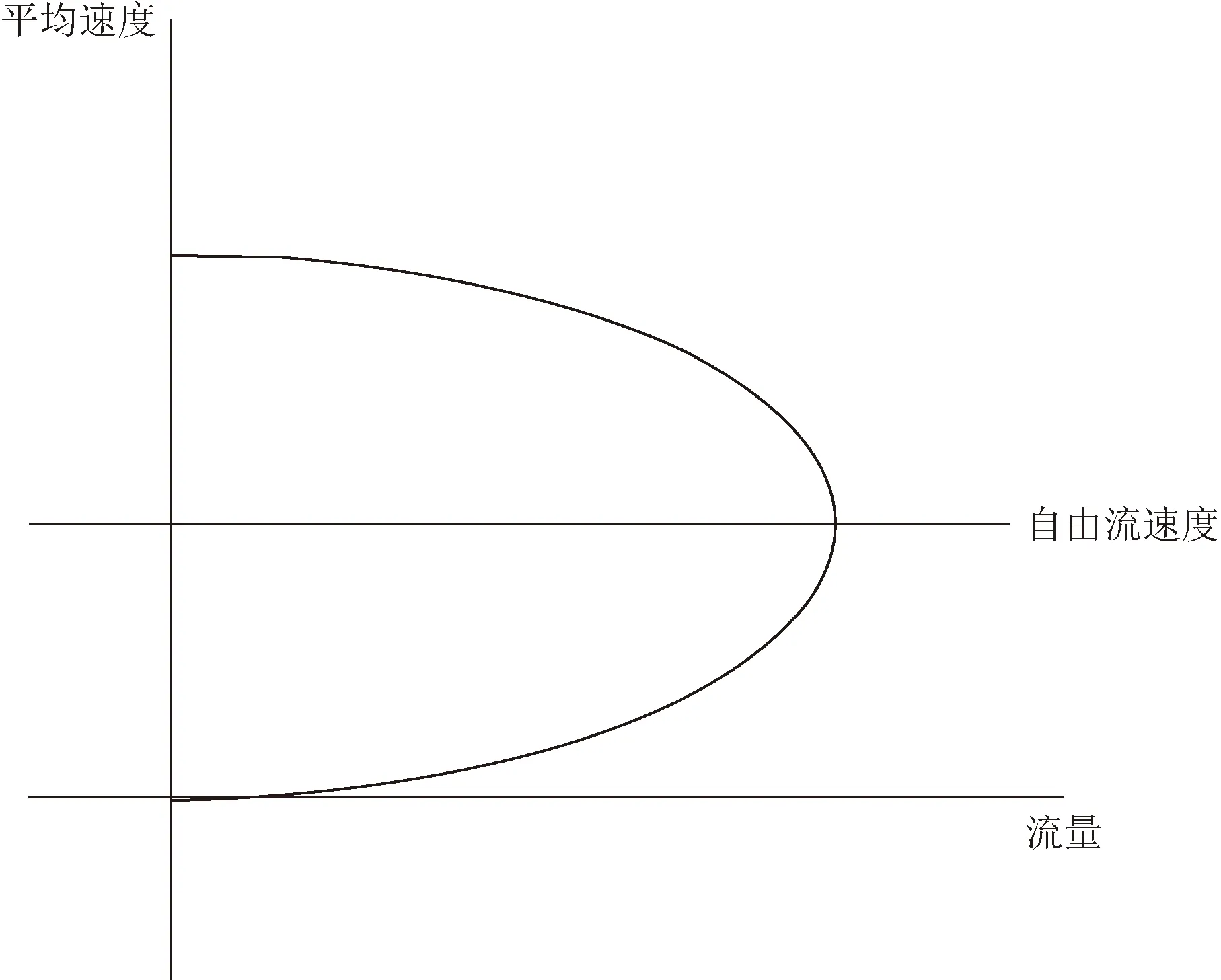
图2 路网平均车速与道路流量关系图
3 基于深度学习的交通预测模型
采用的数据集是成都市10 746辆出租车2018年3月的GPS定位数据,总共包含了1 372 331 359条数据。本数据集的GPS地理信息数据的采样频率是高频采样,每10 s就记录一次出租车的GPS数据,在计算路网速度上具有良好的准确性。并且由于对每条link都做了对应的权重计算,因此在相应道路上的交通拥堵判别上,对比传统的只考虑路网车速的其他拥堵判别法更具有准确性。
数据集的字段如表2所示。
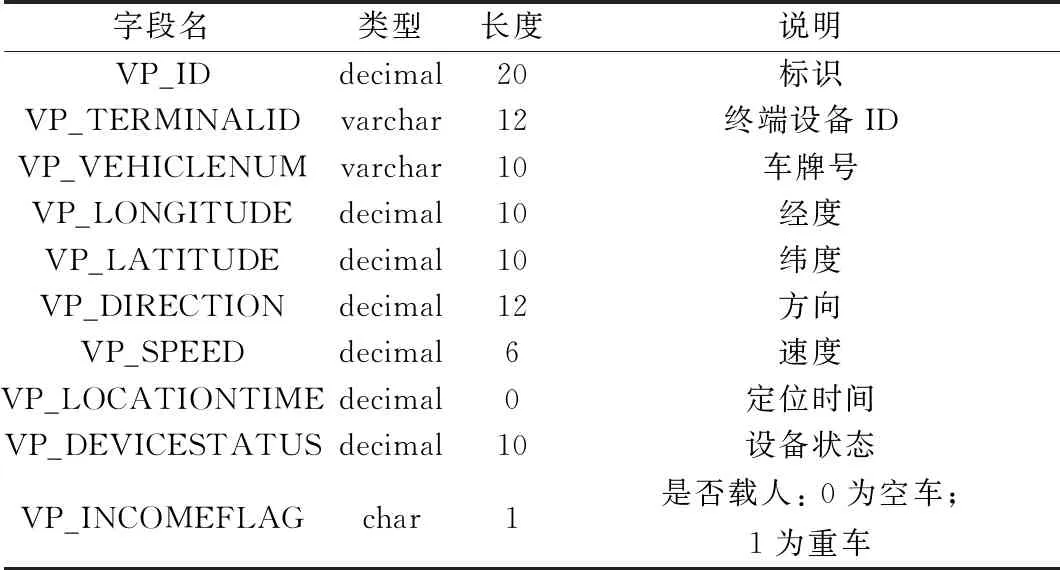
表2 数据集字段及说明
将数据集分为3个部分,以前15 d作为训练集,16~22 d作为验证集,最后9 d作为测试集。把基于网格区域TTI计算得到的成都区域交通拥堵矩阵作为输入数据,每15 min的拥堵矩阵作为一个数据,生成的矩阵可以看作图像的一个通道(channel),因此图像的宽度为7,高度为7。
将预测任务分成如下3个。
任务1:使用过去60 min的TTI预测未来15 min的拥堵情况。
任务2:使用过去90 min的TTI预测未来15 min的拥堵情况。
任务3:使用过去120 min的TTI预测未来15 min的拥堵情况。
使用这3个任务,是为了找出TTI对于哪种时间段来说具有更好的预测作用,便于以后对交通规律进行探索。
3.1 基于BiLSTM的C-BiLSTM预测框架
3.1.1 CNN神经网络
卷积神经网络(CNN)的产生源于对视神经感受野的研究,远早于相关计算模型。虽然不乏数学和其他工程技术的指引,但依然可以认为其中的一些重要性的关键设计理念都是从神经科学中得到借鉴。
CNN模型成功的原因在于它运用二维空间关系(特别是图像中的二维空间关系),达到了降低需要学习的参数个体量的目标。作为第一批能够反复利用反向传播技术进行训练的深度学习神经网络之一,它还在一定程度上提高了反向传播技术的训练性能。在CNN中,图像的一小部分(局部感受区域)被作为神经网络结构的最原始的输出,而图像信息的特征则会被网络中每层都有的滤波器检测到,随后向前逐层传递。图3为一个简单的CNN卷积运算过程的示意图。
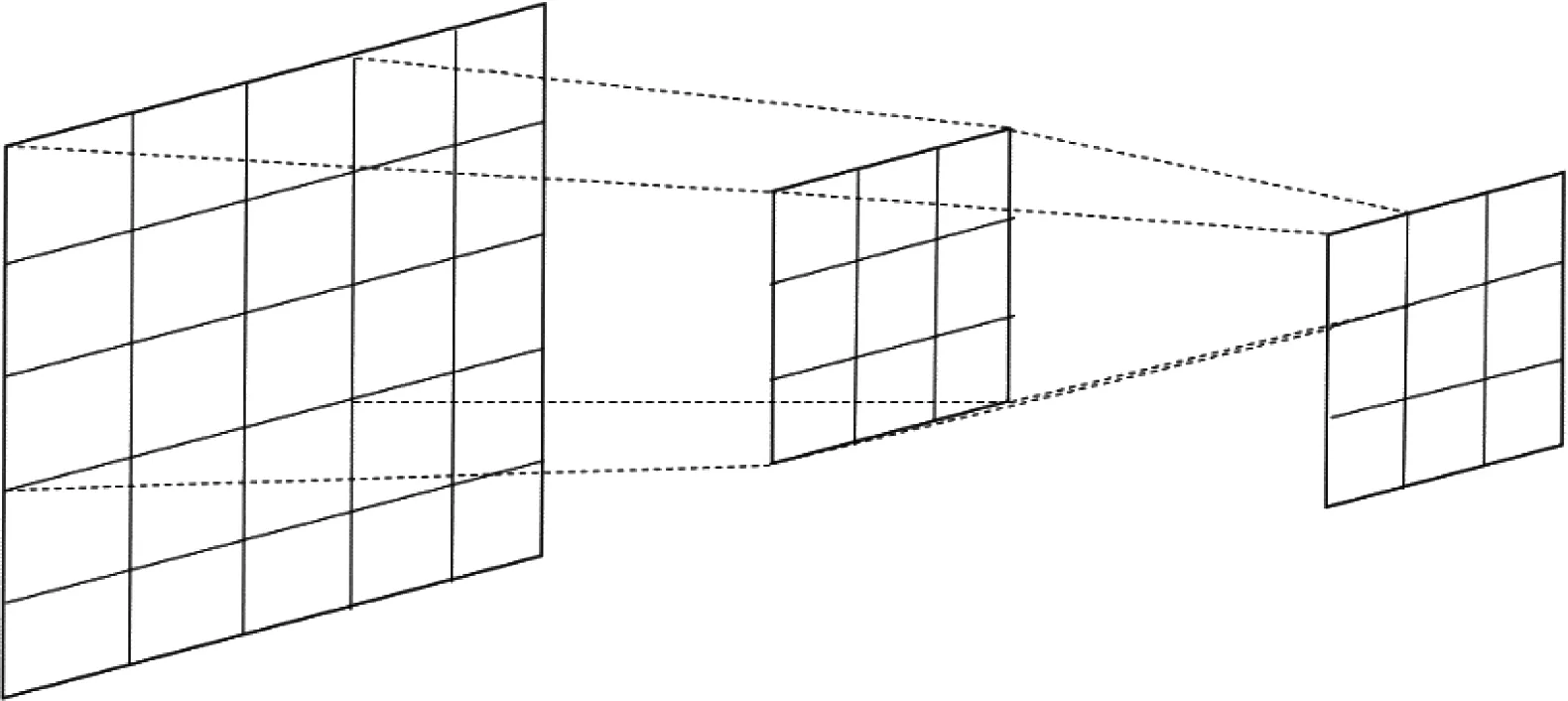
图3 卷积运算过程示意图
3.1.2 BiLSTM 模型
双向长短期记忆(bidirectional long short-term memory,BiLSTM)模型已成功应用于自然语言处理(natural language processing, NLP)和数字图像信号处理领域。因为BiLSTM模型可以同时从数据的不同方向考虑历史数据的时序特征,所以在处理时序数据时,它比单一的 LSTM 的分析处理效果要好得多。
BiLSTM的整体结构是由正向和反向分别堆叠的两个单向LSTM网络组成,其中正向LSTM是计算从开始到结束的输入流量序列,反向LSTM则是计算从结束到开始的输入流量序列。在T时刻,向BiLSTM模型输入两个时序相反的TTI数据,输出则由BiLSTM结构共同决定。其结构如图4所示。
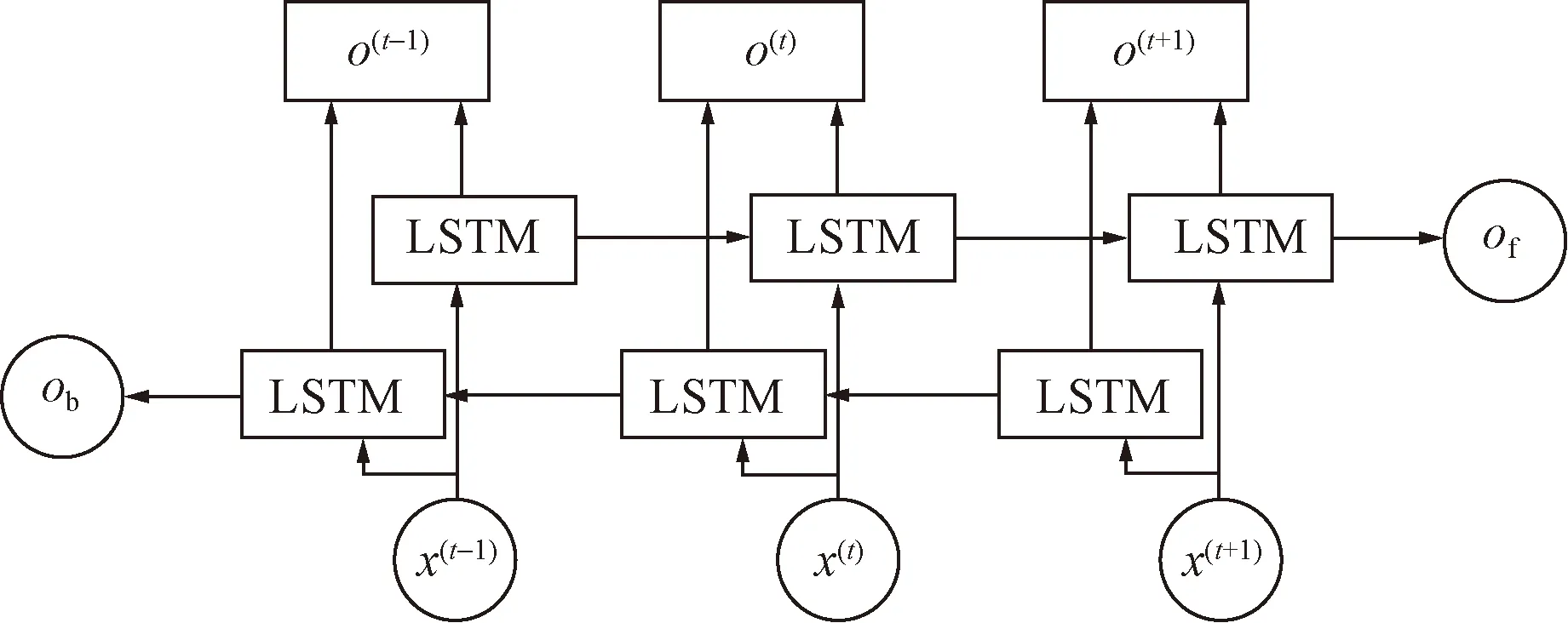
Ob为模型输入;LSTM为长短期记忆;O(t)为LSTM输出;x(t-1)为LSTM输入;Of为模型输出
BiLSTM结构可以综合考虑两个时序方向的交通拥堵信息,对时序特征中的周期特征信息进行加强,从而提高预测精度。
3.1.3 C-BiLSTM 模型结构
为了充分利用TTI交通拥堵系数的时空特征,采用了CNN和BiLSTM的组合模型CNN-BiLSTM进行预测。通过CNN模块提取数据中的空间特征,通过BiLSTM模块提取数据中的时间特征。
首先将构建的成都区域交通拥堵矩阵作为输入数据,生成的矩阵可以看作图像的一个通道(channel),因此图像的宽度为7,高度为7。因为每15 min的拥堵矩阵作为一个数据,根据不同任务,定义不同的通道数。对于交通拥堵系数而言,路段是一个连续的平面空间,因此采用一维卷积神经网络来进行建模。把定义好的数据输入CNN模块,通过CNN模块提取数据流当中的空间特征。CNN模型结构如表3所示。
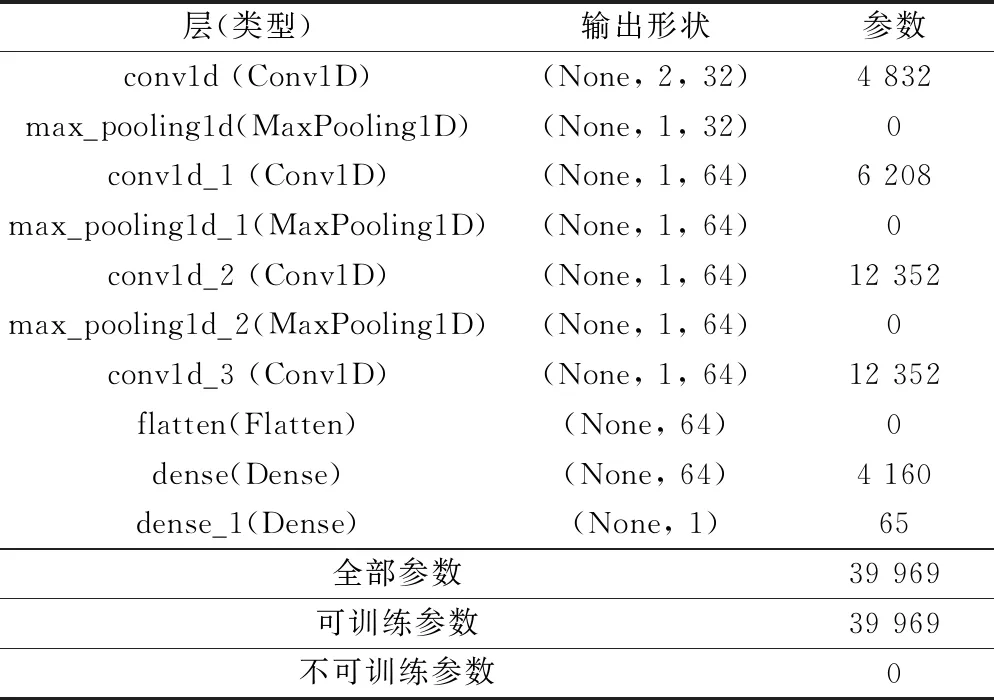
表3 CNN模型结构
然后将输出的数据再输入BiLSTM模块,通过BiLSTM模块提取时间特征,最后连接一个全连接层。CNN-BiLSTM 模型拓扑结构如图5所示。
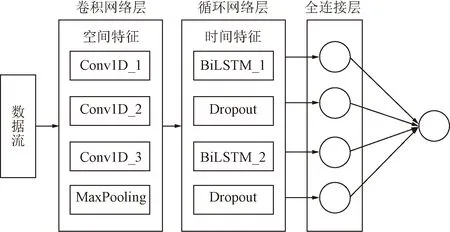
图5 CNN-BiLSTM模型拓扑结构图
3.1.4 CNN-BiLSTM 模型实验结果
从图1的城市区域划分中,选取了第30号区域和第39号区域采用CNN-BiLSTM模型进行预测对比,这2个区域位于市中心附近,具有良好的交通拥堵规律,如图6所示。
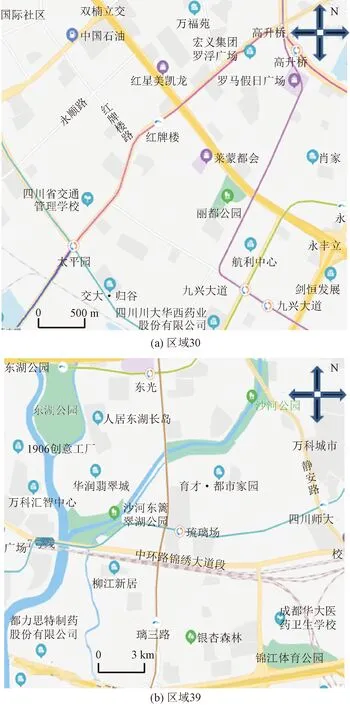
图6 区域30和区域39地图
对于区域30,任务1、任务2、任务3的预测结果如图7所示。对于区域39,任务1、任务2、任务3的预测结果如图8所示。CNN-BiLSTM模型的预测结果如表4所示,CNN-BiLSTM和传统神经网络模型对比结果如表5所示。
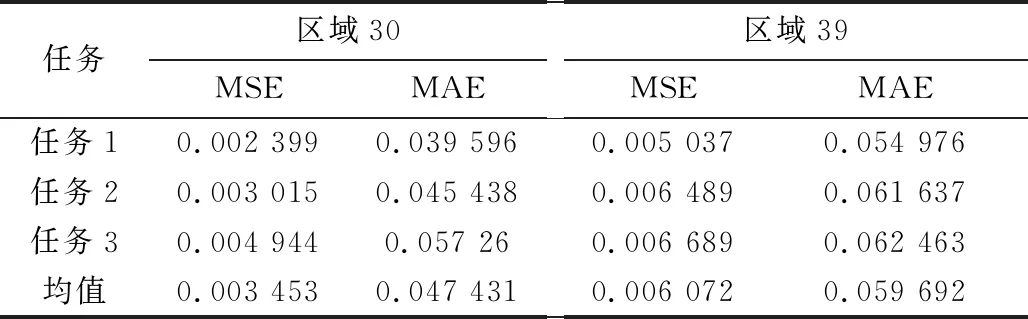
表4 CNN-BiLSTM模型预测结果
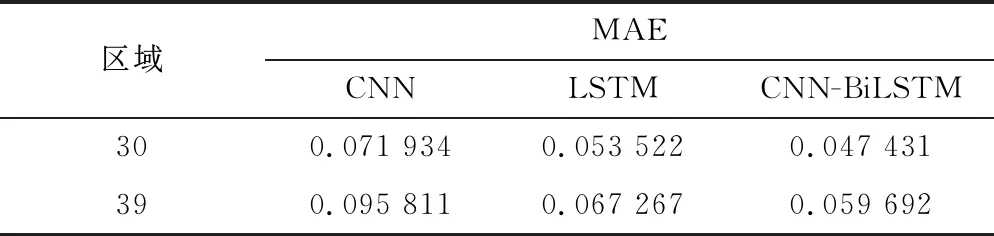
表5 CNN-BiLSTM和传统神经网络模型的MAE对比
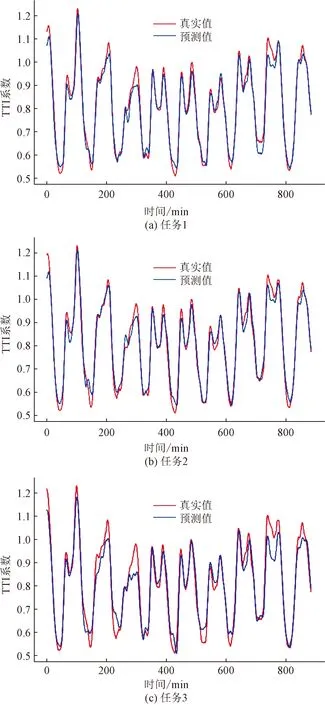
图7 区域30基于CNN-BiLSTM的预测结果图
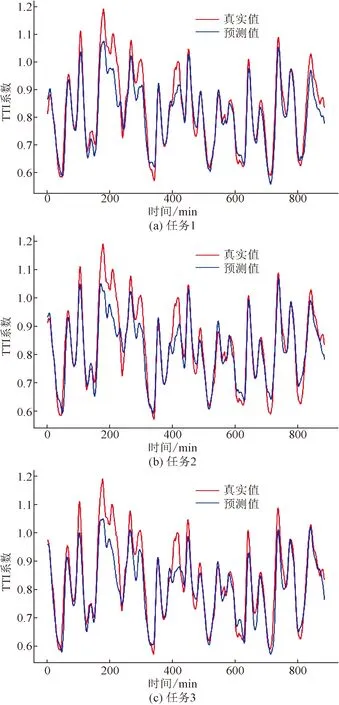
图8 区域39基于CNN-BiLSTM的预测结果图
可以看到,CNN-BiLSTM模型的预测结果相较于传统神经模型CNN和LSTM,预测准确度提升了36%和11%。
3.2 改进预测框架CS-BiLSTM
3.2.1 Softmax 函数的基本原理
Softmax从字面上来说,可以分成soft和max两个部分。max故名思议就是最大值的意思。Softmax的核心在于soft,而soft有软的含义,与之相对的是hard。很多场景中需要找出数组所有元素中值最大的元素,实质上都是求的hardmax。
而hardmax最大的特点就是只选出其中一个最大的值,非黑即白。但是往往在实际中这种方式是不合情理的,比如对于文本分类来说,一篇文章或多或少包含着各种主题信息,更期望得到文章对于每个可能的文本类别的概率值(置信度),可以简单理解成属于对应类别的可信度。所以此时用到了soft的概念,Softmax的含义就在于不再唯一地确定某一个最大值,而是为每个输出分类的结果都赋予一个概率值,表示属于每个类别的可能性。
Softmax函数的表达式为
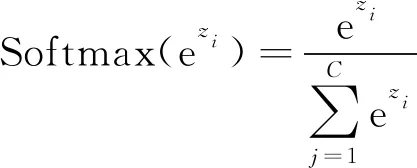
(7)
式(7)中:zi为某种特征;C为特征的总数量。
指数函数的曲线呈现递增趋势,斜率逐渐增大,也就是说在x轴上一个很小的变化,可以导致y轴上很大的变化。这种函数曲线能够将输出的数值拉开距离,达到信息增强的目的。
而且在深度学习中通常使用反向传播求解梯度进而使用梯度下降进行参数更新的过程,而指数函数在求导的时候比较方便。
比如在使用交叉熵作为损失函数时,其表达式为
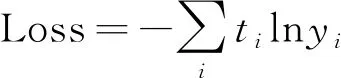
(8)
式(8)中:ti为真实值;yi为求出的Softmax值。当预测第i个时,可以认为ti=1。此时损失函数为
Lossi=-lnyi
(9)
对Loss求导。根据Softmax函数的定义有
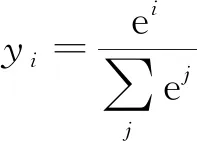
(10)
可以看到Softmax函数可以将多个输出限定在[0, 1],并且满足概率之和为1。则有
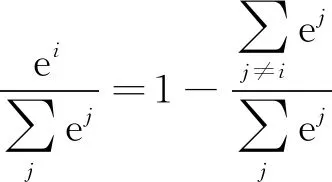
(11)
求导过程如下。
(12)
由推导出来的Softmax函数的求导结果可知,只要能得到yi,那么其结果减1就是反向更新的梯度。因而在模型中加入Softmax函数,并不会对模型的训练增加较大的开销。
因此,Softmax函数具有增强特征信息的能力,并且在模型训练中不会造成巨大的性能损失,非常适合在海量大数据的背景环境下加入神经网络模型的训练过程,达到优化模型能力的目的。
3.2.2 CS-BiLSTM模型结构
基于 Softmax 函数对于特征信息的增强能力,并结合3.2.1节的结论,使用Softmax层对CNN层提取出来的空间特征信息进行增强,将提高神经网络模型对 TTI 预测的准确性。因此,将CNN-BiLSTM模型进行改进,得到CS-BiLSTM模型,其拓扑结构如图9所示。
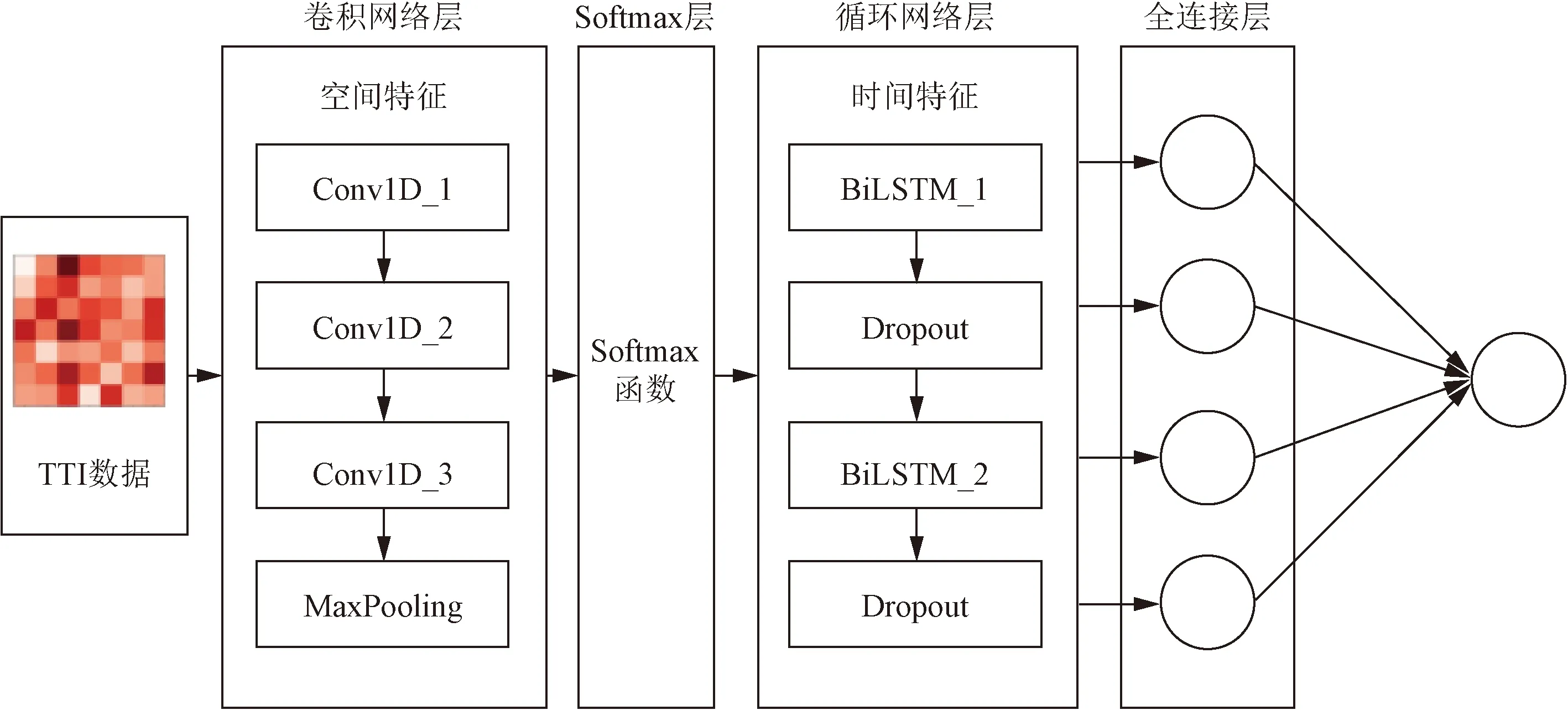
图9 CS-BiLSTM模型拓扑结构图
改进模型的输入是从网格化的交通流数据。其前半部分式卷积层,用于交通流数据的空间特征提取,为了防止过拟合和提高运算效率,卷积层后添加了池化层。后半部分是BiLSMT模型,用于提取交通流数据的时间特征。从拓扑图中可知,将Softmax层加入在卷积网络层和循环网络层之间,旨在用Softmax函数增强卷积网络层提取出来的交通流数据的空间特征。Softmax函数在交通空间特征的增强作用如图10所示。
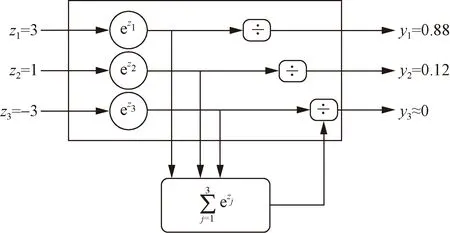
图10 Softmax函数在交通空间特征的增强作用示意图
由式(7)可知,Softmax函数的分母包含了所有的空间特征信息,意味着Softmax函数可以得到每个不同空间特征之间的不同概率之间的关联性。因此,用Softmax层来连接CNN层和BiLSTM层,可以将CNN层的提取出来的空间信息通过这种不同概率之间的关联性,增强其空间特征信息。
3.2.3 CS-BiLSTM模型实验结果
采用CS-BiLSTM模型后,分别对区域30和区域39进行了预测实验,结果如图11、图12所示。预测结果如表6所示,与CNN-BiLSTM对比结果如表7所示。
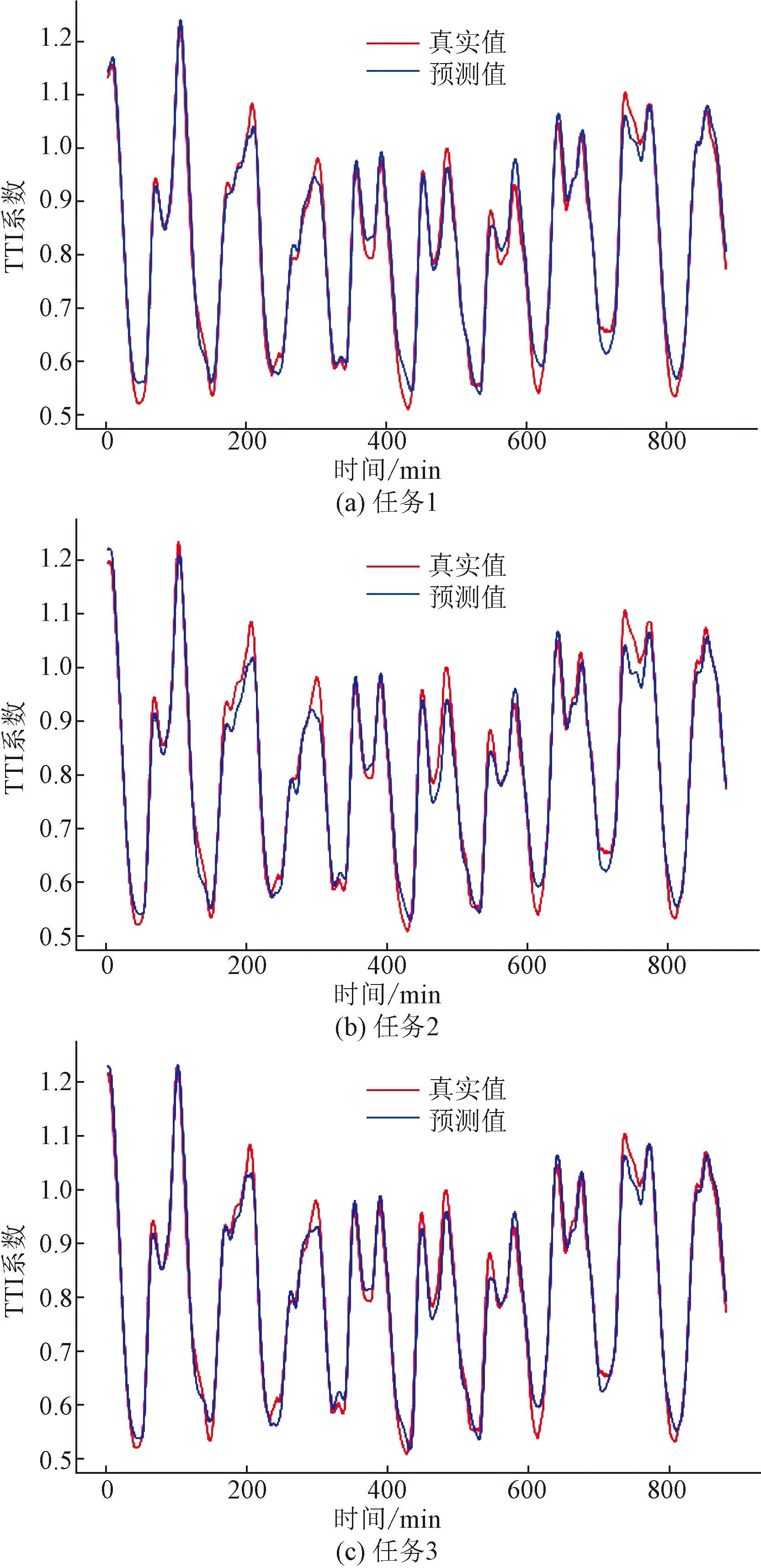
图11 区域30基于CS-BiLSTM的预测结果图
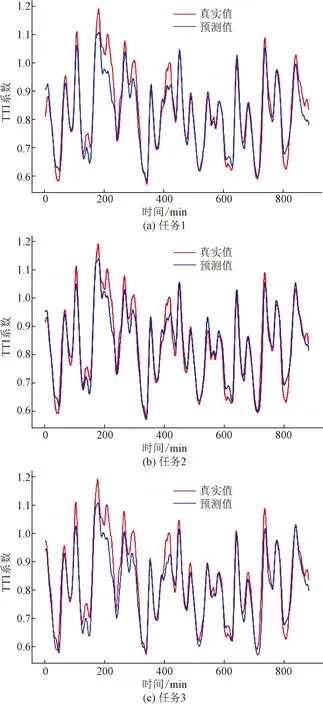
图12 区域39基于CS-BiLSTM的预测结果图
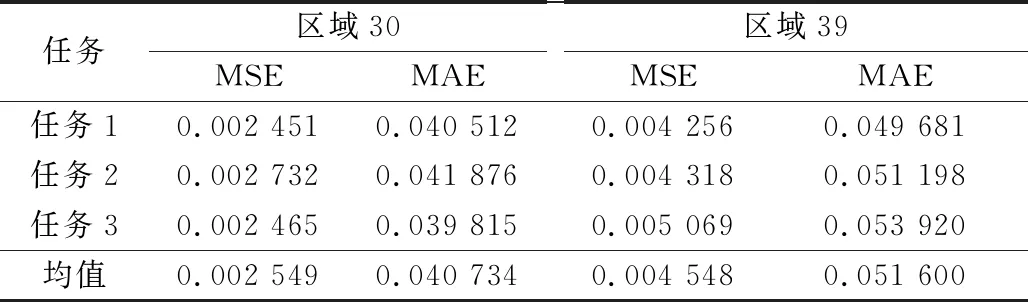
表6 CS-BiLSTM预测结果

表7 CS-BiLSTM模型和CNN-BiLSTM模型MAE对比
可以看到,改进的CS-BiLSTM模型相较于CNN-BiLSTM模型在MAE指标性能上有所提升,综合对比准确率提升了13%。
4 结论
通过实验进行证明后,可得出如下结论。
(1)和传统的交通预测模型的不同,在于没有采用传统的以车辆速度为基准的预测方法,而是使用了TTI作为拥堵系数,该系数结合了道路通行等级,为各个等级的街道都定义了拥堵评判方法,因此较以车辆速度为基准的预测方法更具有准确性。
(2)在采用TTI交通拥堵系数基础上,比较了传统的神经网络预测模型的预测结果,并提出了一种CS-BiLSTM网络预测框架,将CNN处理空间信息的能力和BiLSTM处理时间信息的能力结合起来,提高了预测模型的准确率。
