大型柔性航天器的高精度结构化综合控制

冯焕， 庞爱平*， 周鸿博， 周俊杰， 朱辉， 孟范伟

(1.贵州大学电气工程学院， 贵阳 550025； 2. 东北大学秦皇岛分校控制工程学院， 秦皇岛 066004)

随着航天事业的飞速发展，加之复合材料技术的发展与在航天领域的广泛应用，使航天器的结构日益趋近大型化、柔性化，呈现出多系统模态的特点。这些弱阻尼的柔性谐振模态使系统传递函数的幅值特性呈现大幅度的变化，系统本身的柔性模态又大大限制了带宽的选择(即鲁棒稳定性)，同时复杂的发射环境和在轨运行时的高空环境带来的固有低频扰动对航天器的稳定性和性能造成了干扰，轻则造成性能下降，无法完成任务要求，重则导致航天器控制失稳甚至坠落。

同时，随着航天器承载任务的日益多样化，对大型航天器的指向精度要求也愈加苛刻。既要抑制复杂空间环境所带来的外部干扰和航天器固有的低频谐振干扰，又要满足“高指向精度”的性能要求，同时还要兼顾系统的姿态稳定性、带宽限制，是此类大型柔性航天器控制设计的难点。

以往的研究表明，具有多重性能要求的柔性系统的控制问题，很难采用经典的分析方法来平衡多性能的要求，经典的控制设计方案往往不能兼顾系统的高精度要求和鲁棒性能[1-5]。H∞控制理论是可以将多个性能要求都考虑在设计中的综合控制理论，适用于此类具有多重性能要求的综合控制问题。目前对于柔性航天器稳态运行中的振动控制问题采用的控制方法主要如下。

一是基于分布式和分散观测器的容错控制[6]方案，利用循环小增益定理保证了挠性航天器的闭环稳定性，此外简化了柔性航天器的系统模型，大大降低了柔性航天器容错控制理论分析和工程实践的难度。

二是采用隔振技术降低高频振动和非线性反馈控制使相对姿态收敛到最小的综合控制[7]，满足了柔性航天器相对姿态高精度、高稳定性的要求。

三是基于图论的鲁棒协同控制[8]方案，设计了用于柔性结构形状保持的一致性控制器，克服环境干扰和其他系统不确定性的影响，提高了系统的容错性和鲁棒性。

四是实现高精度的姿态控制和振动抑制的鲁棒自适应控制[9]以及复合干扰观测器和H∞控制方法[10]等，该方案能准确估计外部主干扰并将其抑制，提高了系统的稳定性。但在实践中，由于包含多种不确定性，会降低姿态控制器的性能，须在后续进一步考虑研究。

虽然传统的鲁棒H∞控制设计具有综合多重性能要求的优点，但其在工程应用上也存在局限性[11]，其主要问题是控制器阶次高。阶次高结构复杂的控制器不仅实现起来的代价是很高的，并且在工程实践应用中，还需要根据经验将复杂的控制器分解成多个低复杂度的控制结构来实现，这是一项极大的挑战[12-13]，导致了传统H∞控制器在实际中难以实现。近年来，Gahinet等[11]、Apkarian等[12-14]提出了一种新的综合控制理论，这种新的综合控制方法的设计思路是：首先根据实际需求和控制目标，预先设计好控制器的结构(单一结构化控制器、单环路多控制器协同、多环路的控制结构)，再根据控制对象的具体性能要求，通过加权函数限制输出性能，构建含有多维性能输出综合性能矩阵，最后对这个含有固定结构的控制器进行参数优化，得到最优参数的结构化H∞控制器[15]。其中，权函数的设计显得尤为关键，如何选取合适的参数使性能到达最优也成为许多学者研究的热点问题[16]。

相较传统的H∞综合控制方法，结构化综合控制方法既保留了传统H∞控制的优点，又突破了传统H∞控制的限制，既避免传统鲁棒综合控制多重性能耦合牵制设计的问题，又能以低阶的低复杂度的控制满足多重性能要求，自从被提出就得到了广泛的关注和应用[11-19]。

现针对携带大型太阳能帆板的柔性航天器综合控制问题，在传统综合控制的思路下，采用多控制协同的结构化设计方案。在控制器结构的设计上，首先，充分考虑系统的谐振模态特性，加入内模控制器以增强系统的鲁棒性，减小系统本身的柔性结构带来的谐振影响；同时，根据运行环境的扰动特征，串联陷波滤波器以针对性的抑制外部干扰；以低复杂度的结构化控制器保证系统的多重性能要求，综上通过多控制模块的协同控制来实现综合控制目标，给出既满足综合性能要求，又相较传统综合控制复杂度低的结构化控制器，以减小实际应用的实施难度。

1 系统模型和控制目标

携带大型柔性附件的航天器如图1所示，主要由提供能量的太阳帆板，提供航天器的姿态数据信息速率陀螺仪、精密制导传感器、星跟踪器和用于动量管理的反作用轮、电磁扭矩器，以及一台数字计算机组成。

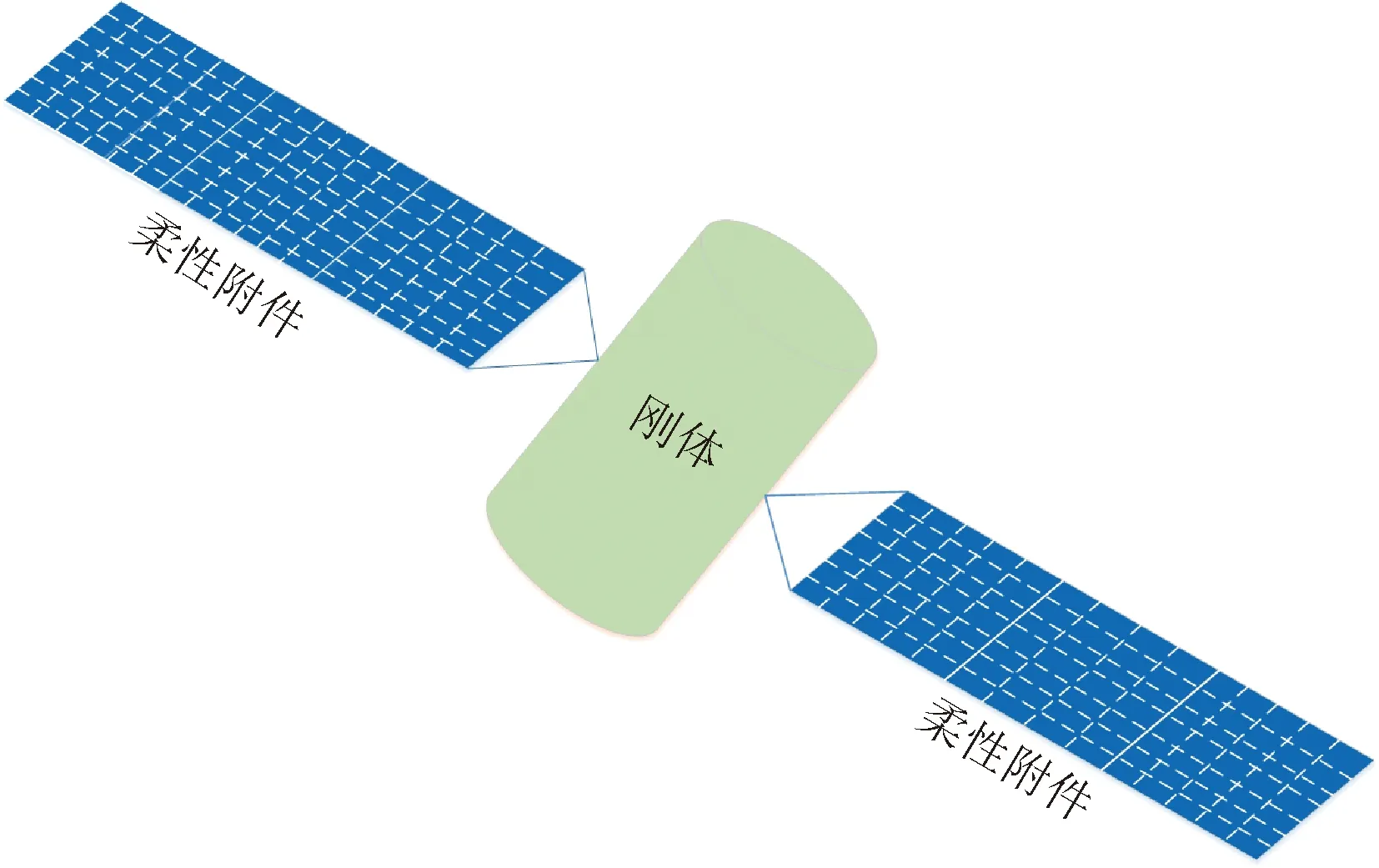
图1 柔性航天器

在构建仿真模型时，仅考虑受抖动影响最大的、也是整个系统中最重要的俯仰轴模型。其控制框图如图2所示。延时环节的引入是为了表征控制器输出到执行器之间的时间差；速率陀螺仪则用一个二阶振荡环节表示；反作用轮存在2.5 N·m的执行器饱和限制；相关符号所代表的含义及参数选择如表1所示。

表1 相关符号含义及其参数

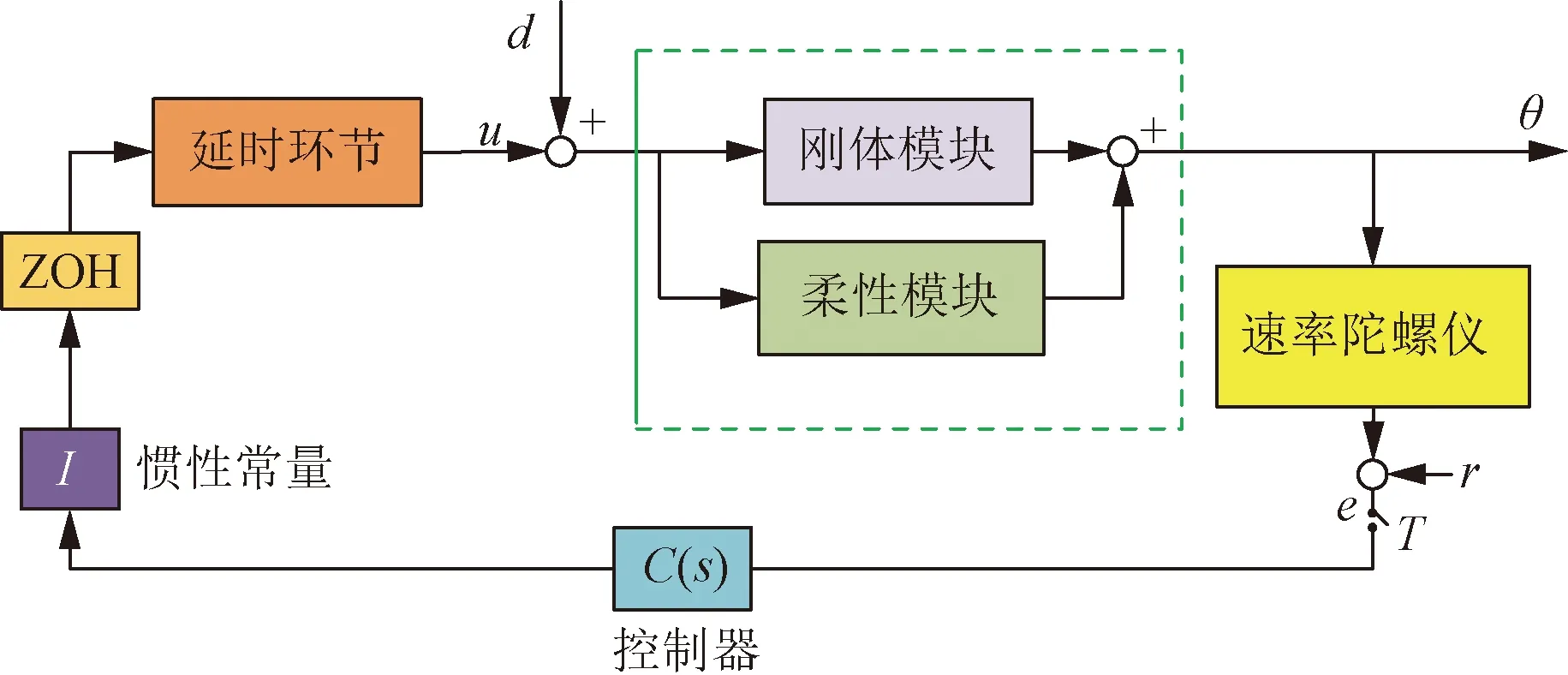
ZOH为零阶保持器

俯仰轴模型可以由一个刚体模型和若干个柔性模块组成，表达式为

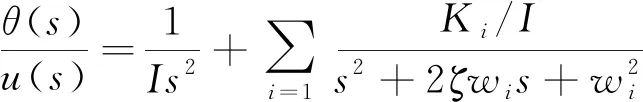
(1)

式(1)中：Ki为第i个柔性模块的柔性增益，i=1,2,…,9；wi为第i个柔性模块的柔性频率。

在控制结构框图中，采用的柔性航天器含有9个柔性模态，相关参数如表2所示。

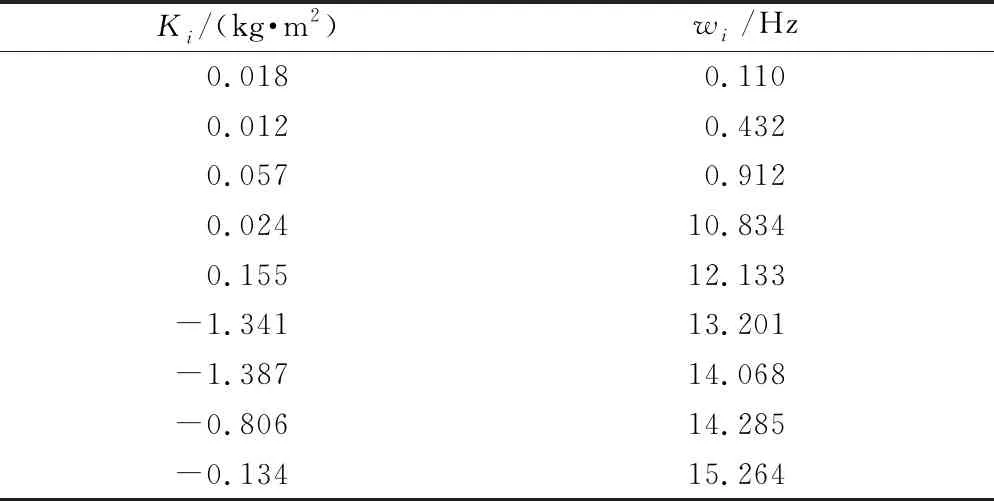
表2 柔性结构增益和频率参数值

系统的开环频率特性如图3所示，从Bode图上可知，截止频率wc仅为0.16 Hz，截止频率极低系统的带宽很小，干扰抑制性能很差。

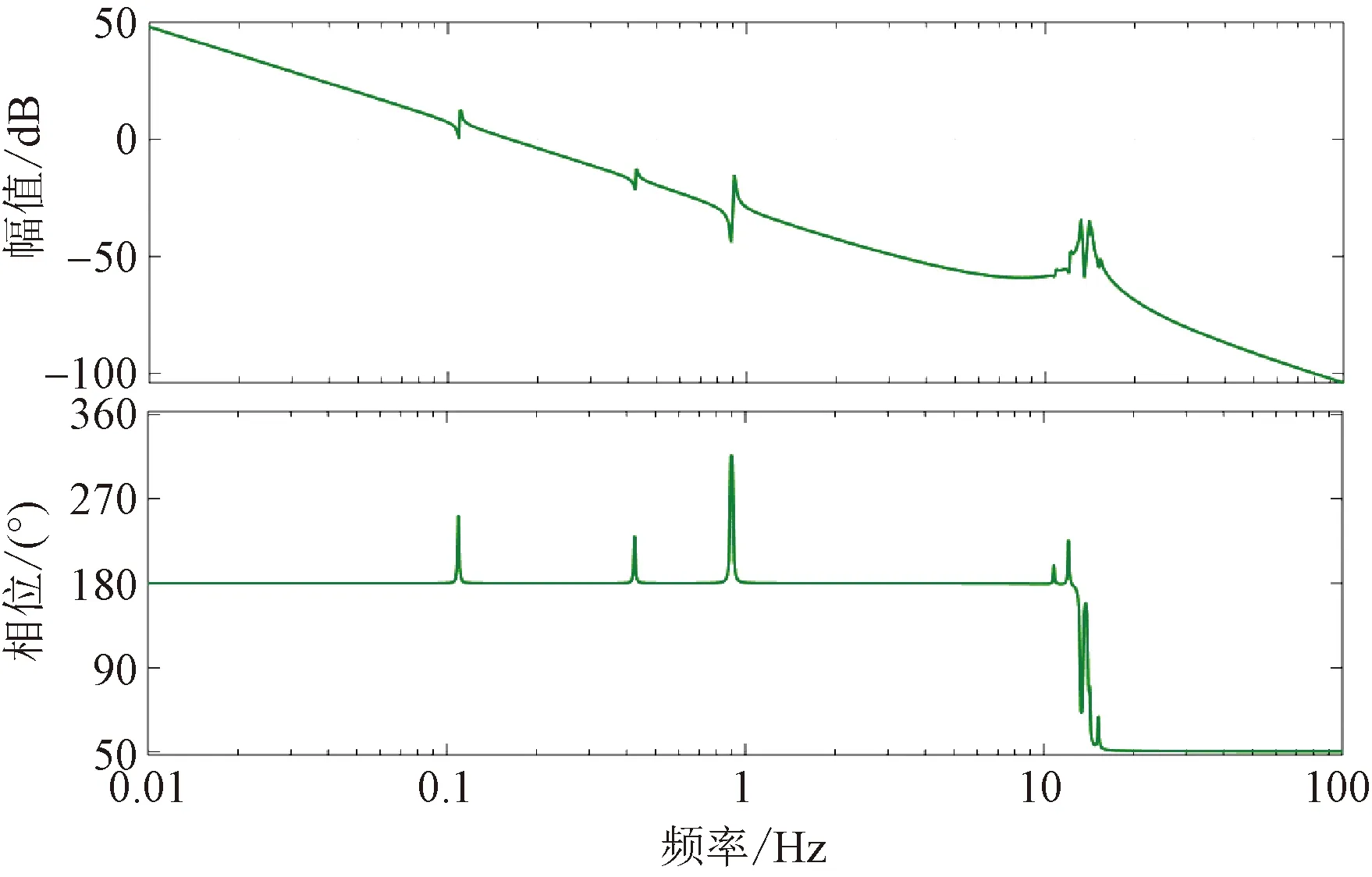
图3 无控制系统下的Bode图

柔性航天器在其复杂的运行环境中，这就要求系统具有良好的控制性能。所设计的控制器应能够有效解决太阳能帆板的扰动抑制、系统固有柔性抑制问题，同时具有一定量的带宽并且满足高指向精度要求。

具体控制要求如下。

(1)带宽限制。要求具有1.5 Hz左右的系统带宽。

(2)扰动抑制。在14 Hz时，对系统柔性结构提供至少6 dB的增益抑制，在0.12 Hz和0.66 Hz时的扰动，至少提供20 dB的附加干扰衰减，保持相角裕度20°以上。

2 控制设计

所建立的被控对象模型无法精确表示实际系统的特性。综合控制的目的是针对被控对象实际存在的未建模动态特性、参数摄动变化、不可预测扰动输入等不确定因素，保证系统具有鲁棒稳定性的条件下同时通过频域整形方法设计系统来满足性能要求。

2.1 标准H∞控制问题

H∞设计时一般都是将设计问题整理成一般标准形式的H∞优化问题，也称为标准问题。

标准问题中的对象称为广义对象G(s)。广义对象有两个输出，一个是表示性能要求的加权输出z，另一个是加到控制器上去的输出y。z可能是某一种数学上定义的信号向量，而y则是真实存在的，是能测量到的输出信号向量。广义对象的输入也是两个，一个是作用于对象上的所有外输入，用向量w表示，另一个是控制器输出作用到对象上的控制输入向量u。广义对象G(s)加上控制器K(s)构成了标准问题中的系统，如图4所示。

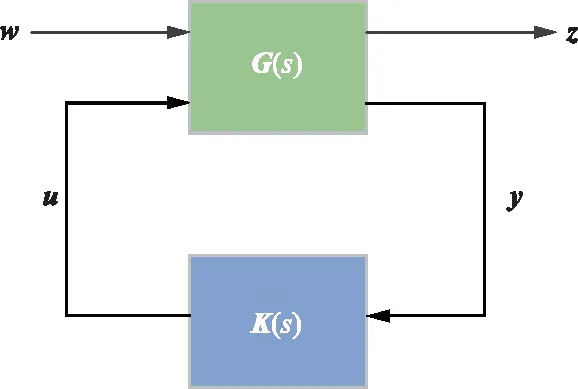
图4 H∞标准问题框图

H∞标准问题是指求解一真有理的控制器K，使从w到z的传递函数矩阵的H∞范数最小，而极小化的约束条件使K镇定G[20]。

相比较一般的H∞设计，结构化综合控制设计的不同在于其控制器是预先设计好的具有固定结构的模块，标准的结构化综合控制设框图如图5所示。

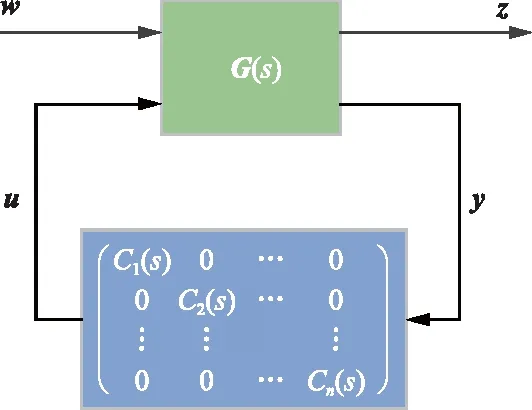
图5 标准结构化综合控制框图

图5包含两个部分，其一是H∞设计中具有固定参数的广义传递函数G(s)，即[wu]到[zy]的传递函数；其二是包含所有可调参数的结构化控制器C(s),C(s)为包含多个控制模块的对角矩阵，即

由于政府及企业相关部门对企业内部控制工作不够重视，导致相关产业、科学技术、人才等方面发展缓慢，这也是我国企业内部控制工作建设经验不足的主要原因之一。由于企业不够重视，相关工作就难以推进，企业内部控制工作大部分仍凭借传统的人工方式进行操作，在企业内部资料处理中会出现遗漏、损坏等问题，导致整个工作进程拖延，对整个企业的发展造成了不必要的损失，不利于企业内部控制工作效率的提高，无法与时代的脚步相契合。企业对于人才的利用效率不高，控制体系管理人才供不应求，企业只好引进外来优秀专业技能人才，导致人才投入成本较高，企业控制体系管理成本也增高。

C(s)=diag[C1(s)C2(s) …Cn(s)]

(2)

控制器中的每一个控制器C(s)，j=1,2,…,n都是一个预定结构的可调块。这个固定的结构控制模块可以是任意的形式，包括复杂的超前与滞后控制器，但是基于优化的控制结构需要尽可能地简单。

与标准H∞设计的理念相同，结构化综合设计的目标也是求取H∞控制器使得系统输入输出的传递函数的H∞范数达最小。

2.2 性能分析及加权设计

大型柔性航天器控制的主要问题是，系统具有多个低频的谐振模态，这些谐振模态使幅值特性呈现大幅度的变化，同时复杂的发射环境和在轨运行时的高空环境带来的固有低频干扰，与系统本身的柔性模态又大大限制了带宽的选择。

要求权函数的选择即要抑制系统所固有的低频谐振扰动，又要达到高的指向精度，还要综合考虑这个柔性系统的带宽限制(即鲁棒性)、稳定程度等综合性能要求。

设T1为r-e的传递函数，系统的稳定程度即传递函数T1到临界稳定点的距离，也是跟踪性能的增益上限，要求即为

‖W1(s)T1(s)‖∞≤γ

(3)

式(3)中：γ为范数指标；W1(s)为加权函数。设计稳定裕度的上限为1，即W1(s)=1。

设T2为d-θ的传递函数，即系统的鲁棒稳定性要求为

‖W2(s)T2(s)‖∞≤γ

(4)

式(4)中：加权函数W2(s)=0.8。

设T3为r-θ的传递函数，系统的带宽要求为

‖W3(s)T3(s)‖∞≤γ

(5)

为限定系统的带宽，可将加权函数选为如式(6)的高通滤波形式,其频率特性如图6所示。

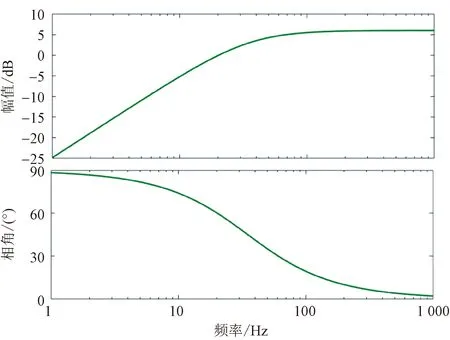
图6 权函数W3(s)的开环Bode图

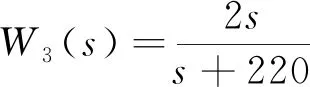
(6)

2.3 标准H∞控制问题

2.3.1 标准H∞控制器

运用2.2节的权函数，利用MATLAB中的hinfsyn函数，经过反复的计算迭代，最终得到γ=8.125时，得出的H∞控制器为表达式为

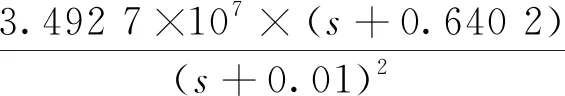
(7)

式(7)中：分子中多项式s2+0.000 360 5s+0.002 128和分母中多项式s2+0.000 22s+0.002 118形成的零点和极点相距很近，可以视作两对偶极子，因此可以将其对消掉。再将分母中引入的微小摄动量0.01去掉，最终简化后的H∞控制器表达式为

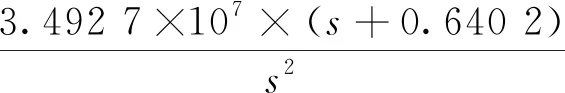
(8)

此时K′h(s)为图2柔性航天器系统结构框图中的控制器C(s)。可以看出为了达到综合性能指标要求，标准的H∞控制器阶次高且结构复杂，这给实际工程应用中带来了极大的挑战。于是给出一种更适用于实际工程应用、可预先设定控制器结构及阶次的结构化综合控制方法。

2.3.2 结构化控制器

结构化综合控制设计首先基于结构化的H∞控制问题，预先设计含参的控制器结构，这个控制器的结构可以是单一的低阶控制器，或多控制模块协同的控制器结构，需要根据控制目标分析系统的结构来设计；然后，分析系统的性能要求，根据控制目标来选择加权函数以保证每个性能的要求，构建含参的加权的解耦输出矩阵；最后根据性能要求和选定的加权函数，求得一个满足多重性能要求的最优控制器参数。

针对上述控制目标，结合本例中系统的柔性模态和固有的扰动频率。给出多控制模块协同的结构化综合控制策略，根据系统特定的谐振模态，在控制器结构中加入内模控制器、陷波滤波器、串联比例-积分-微分(proportion-integration-differentiation，PID)控制器，以低阶的结构化控制器来满足系统的多重性能的要求；设计如图7所示的结构化综合控制器。

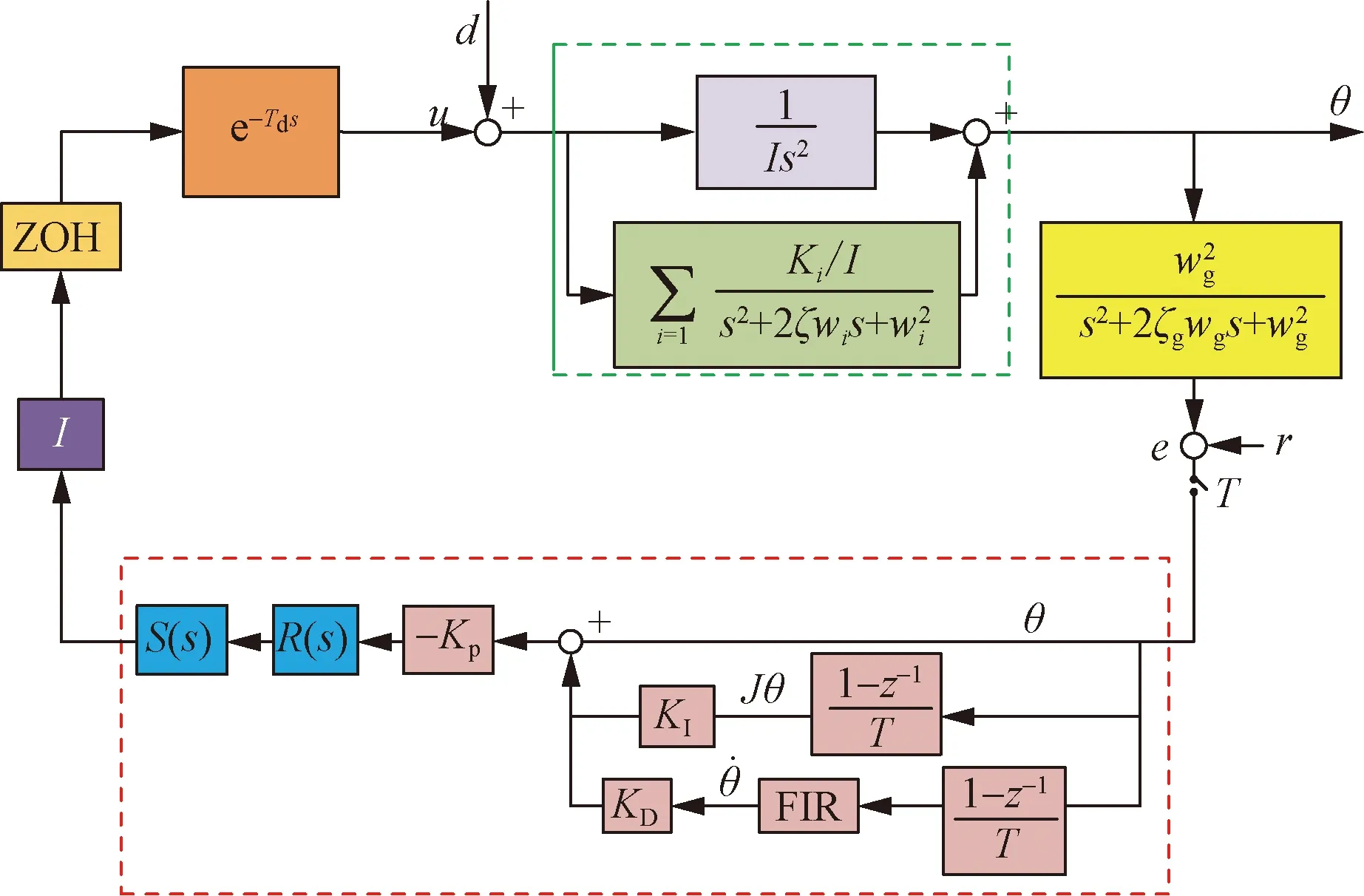
图7 控制系统框图

图7中下面红色虚线框内为这个系统的结构化控制器，其中S(s)、R(s)模块是固定参数的，其他模块是可调参数的，这个结构化综合控制器由三部分组成。

1)内模控制器

针对系统的谐振模态所设计的抑制谐振扰动的内模控制器S(s)表达式为

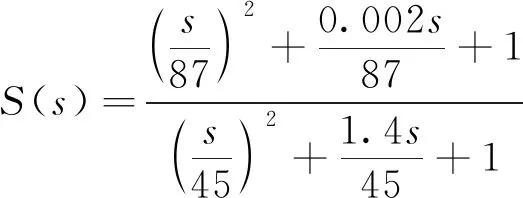
(9)

其频率特性如图8所示，其目的是针对14 Hz处的系统振动，通过增加系统的阻尼，来达到减小系统振动的目的。

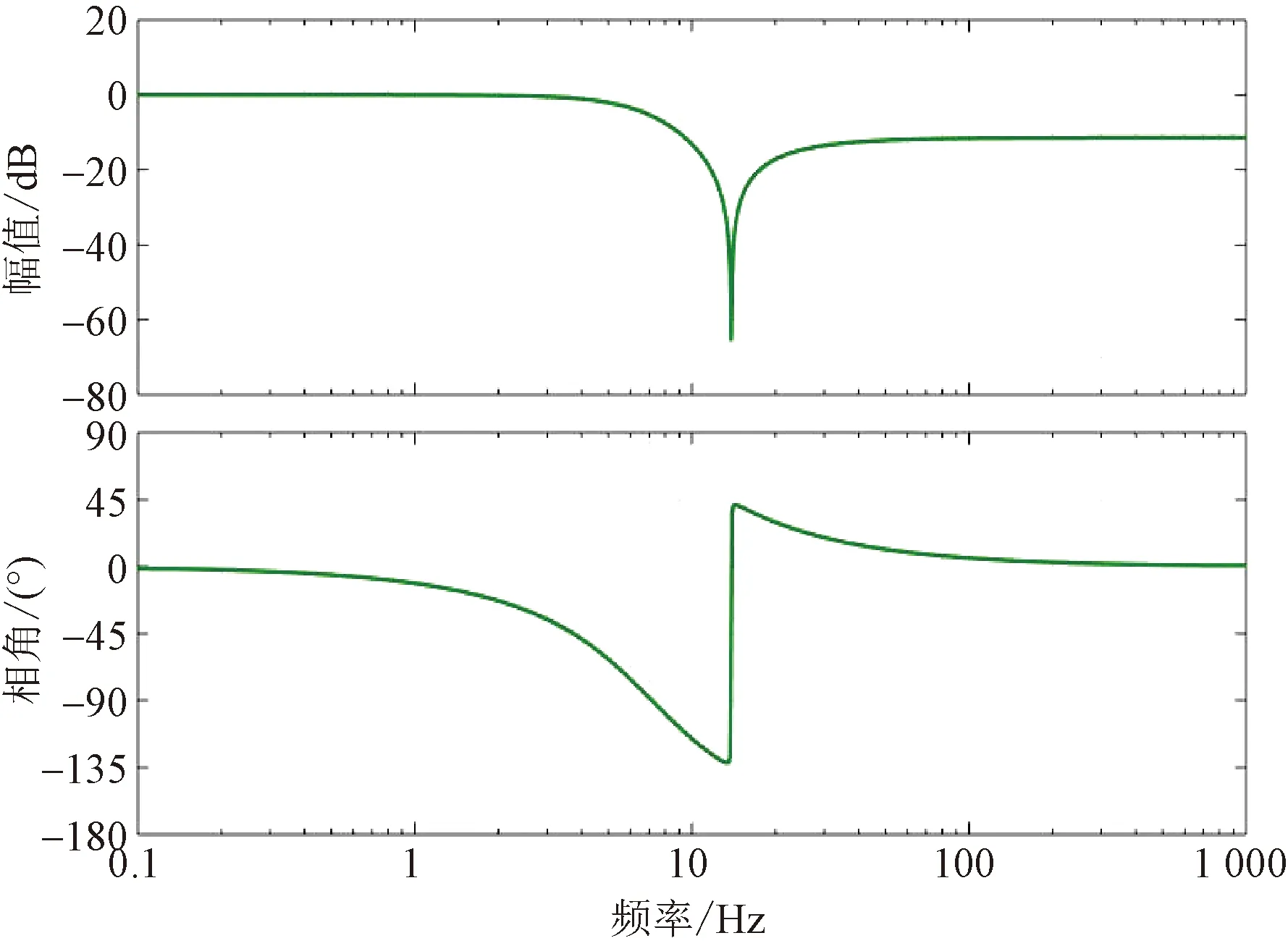
图8 内模控制器S(s)的Bode图

2)陷波滤波器

针对空间环境的扰动特性设置的陷波滤波器R(s),以保证对0.12 Hz和0.66 Hz太阳能帆板的扰动，在不影响系统中频段稳定性的前提下，系统应该能够对该扰动提供足够的抑制的作用，其Bode如图9所示。

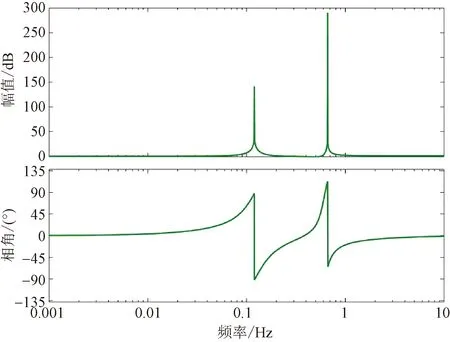
图9 陷波滤波器R(s)的Bode图

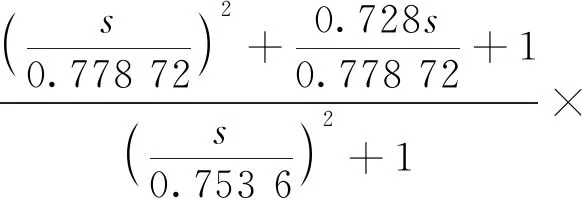
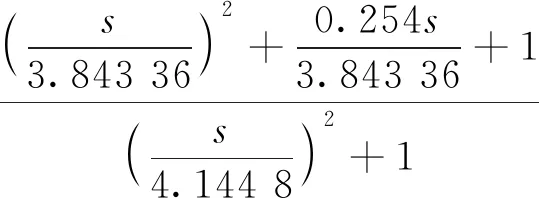
(10)

3)PID控制器

针对保证系统姿态稳定所设的可调参数PID控制器，这个PID控制器的速率路径加有一个FIR滤波用来提供一定的增益抑制。

综合考虑系统的性能要求和控制器的实现成本问题，设计如式(11)所示的控制器。

K(s)=KP(1+KI/s+KDs)R(s)S(s)

(11)

式(11)中：KP、KI、KD为待优化参数。

对于已设计好控制器结构和加权函数的结构化H∞优化问题，综合考虑柔性系统的控制性能要求，通过优化可调参数KP、KI、KD得到满足式(12)的最小γ值为

‖H‖∞≤γ

(12)

在求取结构化H∞控制器中的最优参数时，将式(3)～式(5)中的T1、T2、T3应用线性分式变换(linear fractional transformation，LFT)[17-19]提取含有参数的结构化控制器C，以线性分式形式P1、P2、P3来进行参数优化，即

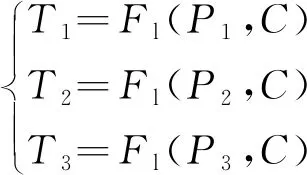
(13)

针对结构化控制器C(s)中含有分子分母参数耦合的问题，对于任意的有理传函R(a)都可以转化生成一个线性分式变化的形式，即

R(a)=Fl(M,a⊗I)

(14)

式(14)中：M为R(a)的线性分式变换；a为可调参数;符号⊗为克罗内克积，表示两个矩阵间的运算。所以图5所示的标准结构化综合控制设计可转换为如图10所示的LFT标准形式进行优化设计。转换后就不再存在耦合的问题。

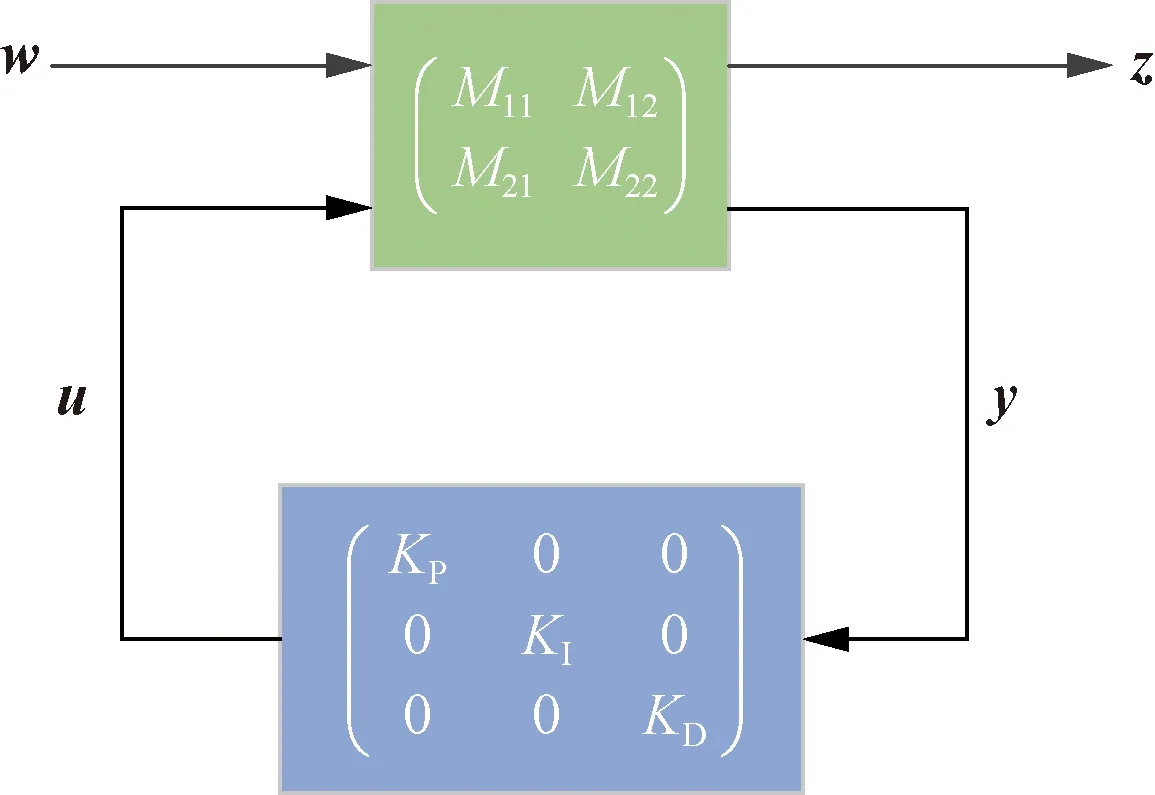
图10 LFT模型

经过反复的迭代计算得到图7中的结构化控制器的最优参数如下：KP=8,KI=0.5,KD=0.95。

最终得到的结构化综合控制器为

K(s)=8(1+0.5/s+0.95s)R(s)S(s)

(15)

3 仿真分析

图11为系统开环频域的Bode图。根据图11可知系统的截至频率约为1.6 Hz，满足了不低于1.5 Hz的带宽要求。同时针对高频谐振模块的振动抑制，提供了超过100 dB的增益抑制。所以所设计的结构化综合控制器在抑制固有谐振干扰的同时，又能满足一定的带宽要求。

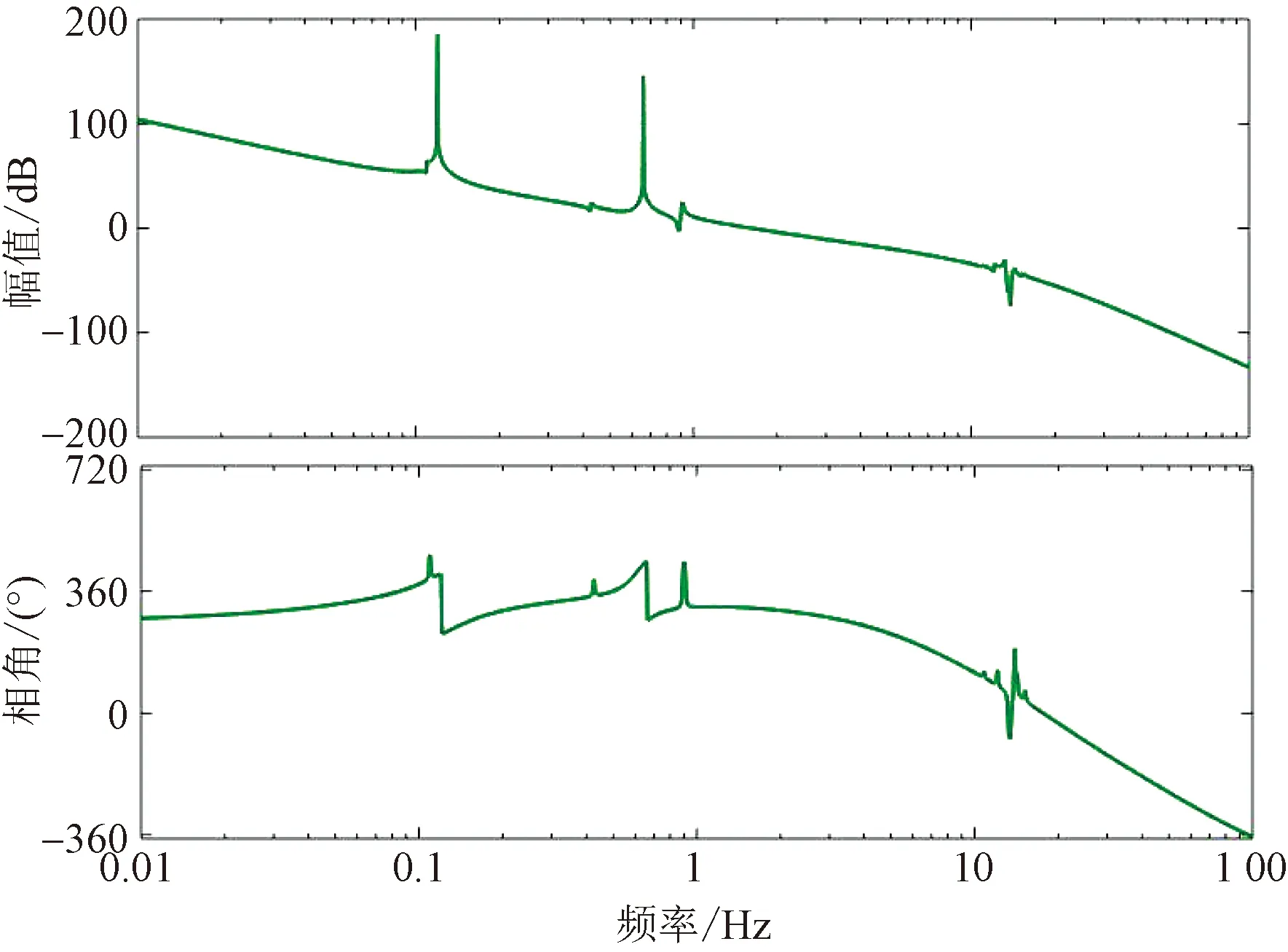
图11 系统开环Bode图

在设计的结构化综合控制器下，系统的时域响应和控制器输出分别如图12和图13所示，可以看出，在不超过反作用轮2.5 N·m的执行器饱和限制下所设计的控制器能够为0.12 Hz和0.66 Hz的抖动提供了远超过20 dB的增益衰减，满足了振动抑制和指向精度的要求。图14为系统的闭环Bode图也刚好证明了这一点。

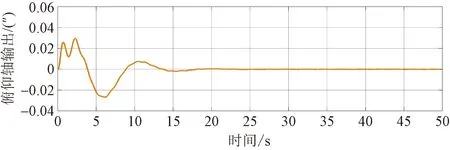
图12 系统的时域响应

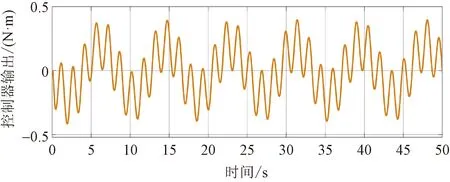
图13 控制器输出

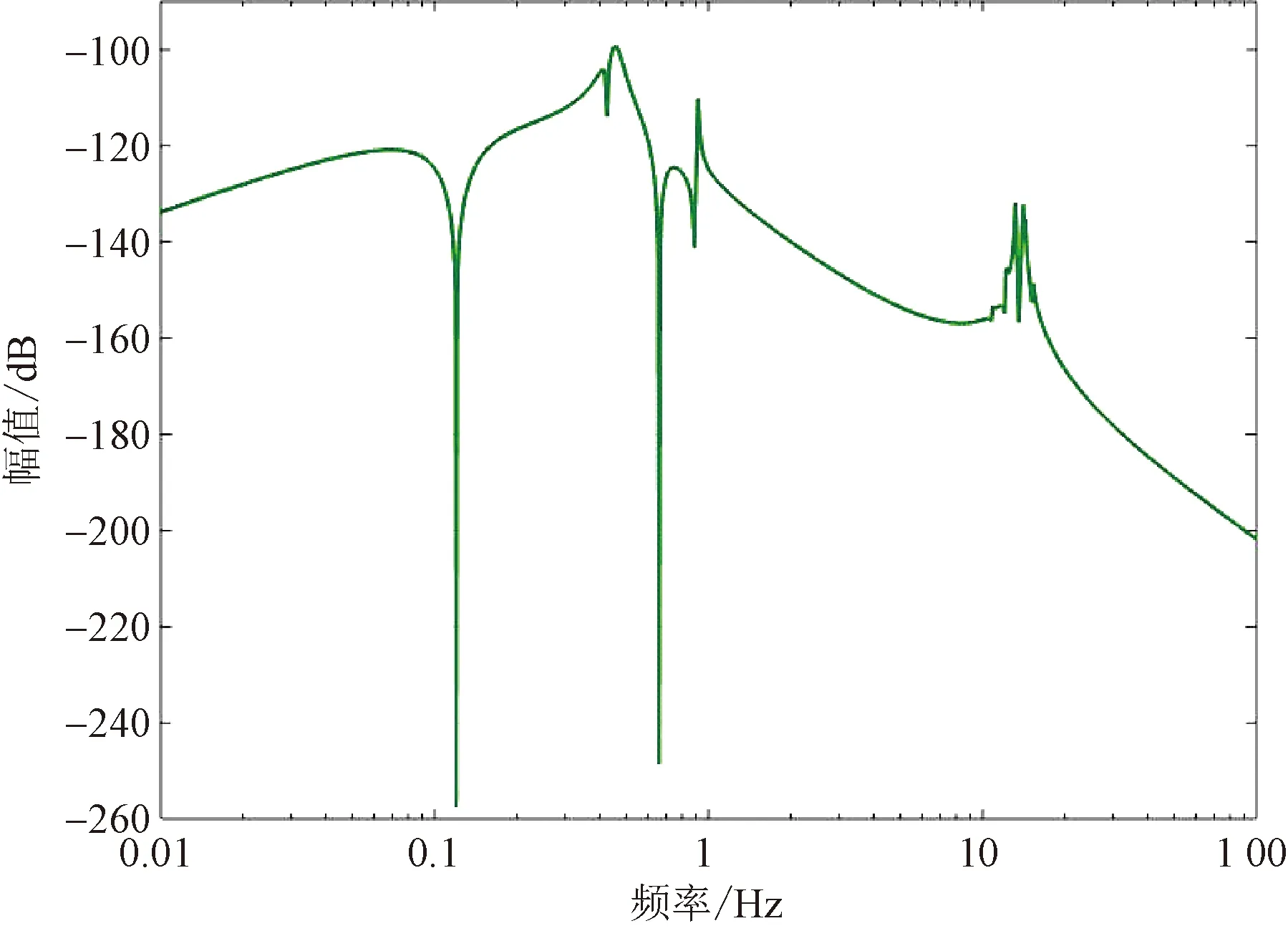
图14 系统闭环Bode图

由图15所示的时域响应可知，在同样的加权函数下，两种控制器均可在一定时间内，完全抑制太阳能帆板扰动的影响，达到所需要的控制性能指标要求具有稳定性。在结构化综合控制的作用下，系统的超调量为2.101%、峰值时间为0.711 s，调节时间13.562 s。而传统H∞控制器的超调量为2.31%、峰值时间为0.876 s，调节时间为14.227 s。可知结构化综合控制在动态性能指标上明显优于传统的H∞控制切控制器的阶次更低，在针对0.12 Hz和0.66 Hz的柔性结构振动具有非常好的抑制效果。

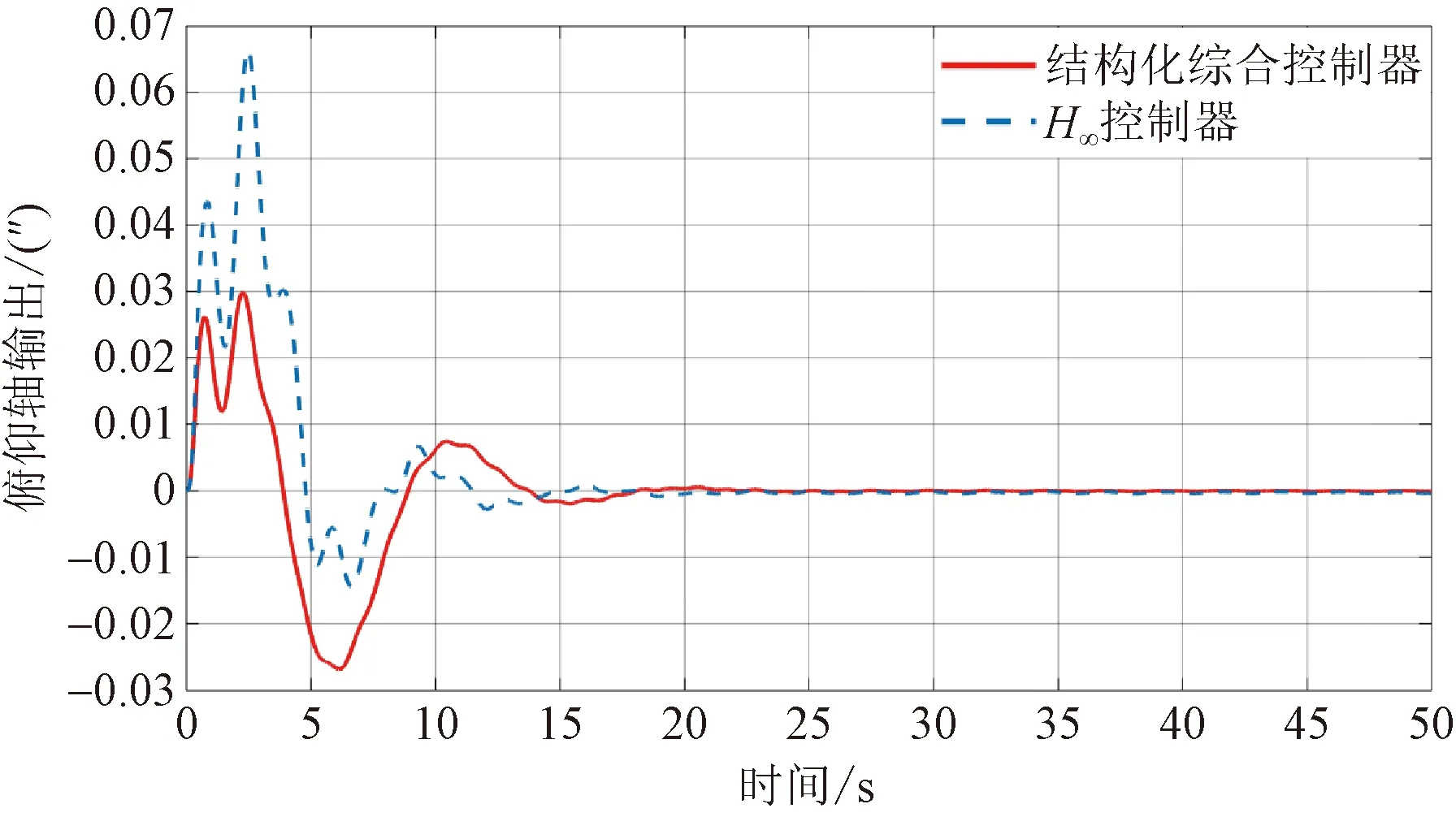
图15 结构化综合和传统H∞控制下的时域响应仿真对比

4 结论

针对携带大型柔性附件的航天器所面临的带宽不足、系统指向性精度低、柔性结构振动等综合性控制问题，采用了结构化综合控制器的实际方案，通过选择适当的加权函数，最终提出了一个满足控制要求的结构化控制器。根据仿真表明，此控制器能够有效抑制大型柔性附件在0.12 Hz和0.66 Hz时的振动问题，在保证高指向精度的同时，又能兼顾姿态稳定性、带宽等要求。相比较传统的H∞控制器，结构化控制器具有复杂程度低、系统阶次较低、工程造价和实施难度都比较低的优点，且所提供的控制性能更佳。