自适应细菌觅食算法的局部放电定位
2022-11-16郭雪婷杨俊杰薛乃凡章弘凯
郭雪婷, 杨俊杰,2*, 薛乃凡, 章弘凯
(1.上海电力大学电子与信息工程学院, 上海 201306; 2. 上海电机学院电子信息学院, 上海 201306; 3. 新能源电力系统国家重点实验室(华北电力大学), 北京 102206; 4. 上海大学机电工程与自动化学院, 上海 200444)
局部放电(partial discharge, PD)是变压器产生绝缘劣化的主要因素之一,也是其绝缘进一步劣化的重要征兆和表现形式。PD源检测是目前变压器绝缘状态评判和估计的重要方法[1-3]。PD源位置的精确定位能够准确、快速地反映变压器的绝缘情况,有助于及时制定相应的维修措施,保证设备的运行稳定性和可靠性。因此,变压器的PD源监测和定位对保障电力系统的安全运行具有十分重要的意义。
目前,PD源定位的检测方法主要包括脉冲电流法、超声波定位法和特高频定位法。由于现场的干扰,脉冲电流法难以在设备运行情况下进行测试,其抗干扰能力较差。由于脉冲电流法测量频率较低,频带窄,测试中包含的信息量相对较少。由于超声波在传播过程中易衰减,传播速度不稳定,定位精度较低;特高频法抗干扰能力强、灵敏度高,已成为PD源定位检测的重要方法[4-6]。
针对基于特高频检测方法的PD源定位,国内外学者进行了充分的研究,主要聚焦于到达时间差法(time difference of arrival,TDOA)[7-9],即利用特高频信号到达各个传感器间的时延差来估计PD源的位置。在PD源定位过程中,首先基于TDOA方法,根据电磁波信号到达接收天线的不同时间延迟,建立非线性方程组。通过非线性最优解方法对方程组进行迭代求解,得到PD源的精确位置。在求解方程中寻找最优解的方法包括粒子群优化(particle swarm optimization,PSO)算法[10]、牛顿拉夫逊(Newton-Raphson)法[11]、最小二乘法[12]、遗传算法[13]等多种方法。传统算法计算较为复杂,对初值的选择要求很高,当初值选择不当时,定位结果不易收敛,甚至发散。在启发式算法中细菌觅食算法(bacterial foraging algorithm, BFA)是通过驱化、复制和分散3种行为来进行优化求解,易跳出局部最优解,得到全局最优解,但其搜索步长是固定的,会出现过早收敛等情况,从而降低全局寻优能力。针对以上情况,结合细菌觅食算法具有的特性,提出了一种自适应惯性权重对游走步长进行改进的细菌觅食算法 (adaptive inertia weighting-bacterial foraging algorithm, AIW-BFA)。AIW-BFA通过自适应调整搜索步长,同时满足全局寻优与局部寻优,以提高定位精度,并与PSO和BFA算法进行对比。
传统的PD源定位算法往往不能给出正确的PD位置,由于变压器内部存在铁芯绕组等有源部分,使得电磁波在传输过程中会发生反射、折射和衍射等情况,对PD源的定位构成了巨大的挑战。文献[14]将铁芯与绕组构建为圆柱体,提出了一种切线模型,结合Dijkstra算法解决信号在变压器内部遇到铁芯等障碍物的传输情况。文献[15]提出概率网格搜索定位方法,通过划分网格构建离散数值模型,以概率方式进行的网格搜索以找到最可能的PD源位置。文献[16]首先采用广义互相关法估计各个传感器接收信号的时延,之后基于非线性球面方程组的筛选并剔除误差较大的时差,随后结合人工蜂群法来实现局部放电源定位。上述方法存在当遇到障碍使得时延与理论值相差较大而被误剔除的情况。且基于构建时间库的方法,其搜索过程的位置点是固定的,计算量较大。
为解决上述问题,在应用AIW-BFA时,现引入特高频信号在变压器内从PD源到传感器的路径距离计算模型,解决遇到铁芯等障碍物的情况,来降低时延误差,实时对搜索过程中的估计位置进行修正,以提高搜索灵活度和对PD源的定位精度。
1 计算模型
在三维空间中,至少同时需要4个传感器来确定变压器内局部放电源(PD)的位置。假设从局部放电源发出的电磁波向四周传播,通过电磁波到达各个传感器的时延建立并求解非线性方程组,来确定PD源在空间内所处的位置。确定PD源位置的空间示意图如图1所示。
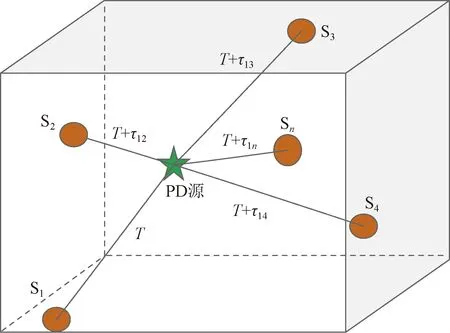
S1、S2、…、Sn代表各个传感器;T为局部放电源发出的电磁波到达参考传感器S1的时间;τ1a为实际PD源到Sa和S1之间的时延,a=2,3,4
1.1 基于TDOA的PD源定位原理
变压器内,特高频信号到达各个传感器的时延关系如图2所示。
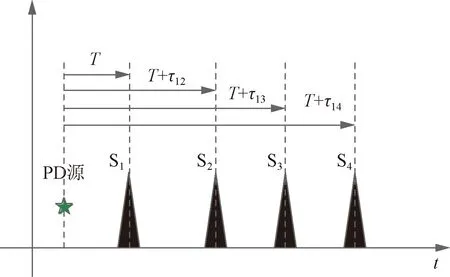
图2 PD源与各个传感器之间时延示意图
通过传感器获得PD源到达各个传感器的时延,来获得变压器中PD源的位置坐标,目标函数为
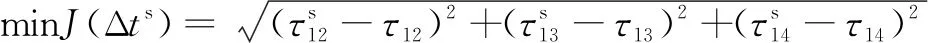
(1)
(2)
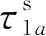
1.2 PD源与传感器间路径计算模型
假设PD源的空间位置坐标为(x,y,z),各个传感器的空间位置坐标为Si(xi,yi,zi),i=1,2,…,n。基于TDOA原理,为简化计算,引入δi用来表示特高频信号到Si传输过程中发生绕射的部分较直线传播相差的距离。列出以下方程。
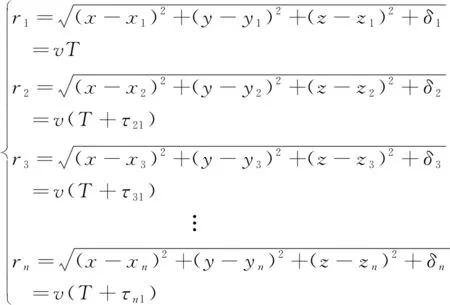
(3)
式(3)中:v为电磁波在变压器内的传播速度;T为局部放电源发出的电磁波到达参考传感器S1的时间;τi1为PD源发出的电磁波到达第i个传感器与S1之间的时间差,i=2,3,…,n;(x,y,z)为求解过程中估计的PD源位置。
基于最短光程原理,TDOA的求解转化为PD源到各个传感器间最短距离的求解。由于变压器内部往往存在铁芯、铜导体等内部结构的阻碍,使得电磁波不能直接穿透而发生边缘、表面等不同程度的绕射[17]。由于层间绝缘,绕组之间有相当小的间隙,理论上电磁波可以在一定程度上通过它们传播,但是实际上会受到极大的衰减,使得实验过程中无法检测到穿过匝间绝缘的电磁波[18],此时可忽略在绕组间的传播路径[19]。因此在建立模型过程中,为减少仿真时间,对模型进行了一定的简化,将铁芯与绕组构建为圆柱体结构(图3)。
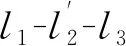
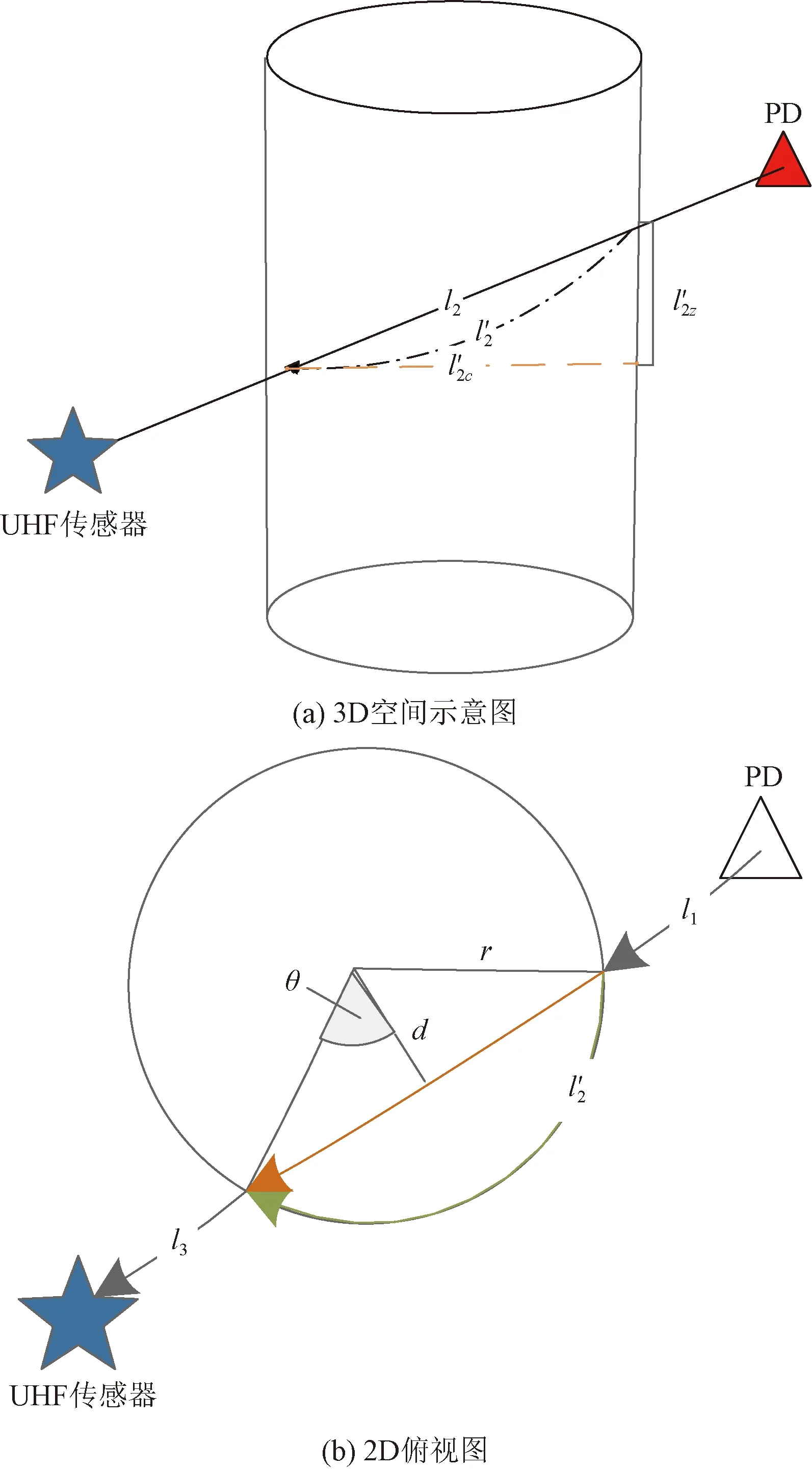
图3 PD源到传感器之间的路径计算模型
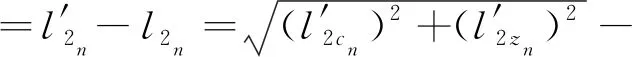
(4)
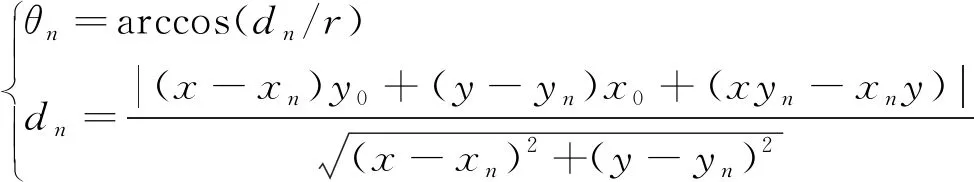
(5)
式中:lc为l在XY平面上的映射;lz为l在z轴上的映射;r为铁芯的半径;θn为r与dn之间的夹角;dn为铁芯在二维视图中的圆心到PD源与第n个传感器之间的直线的距离。利用相似三角形的原理,得
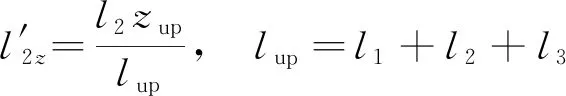
(6)
式(6)中:l2为PD源与传感器传播路径之间与铁芯相交的线段;lup为PD源与传感器间的距离;zup为PD源与传感器在z轴方向上的距离。
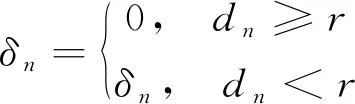
(7)
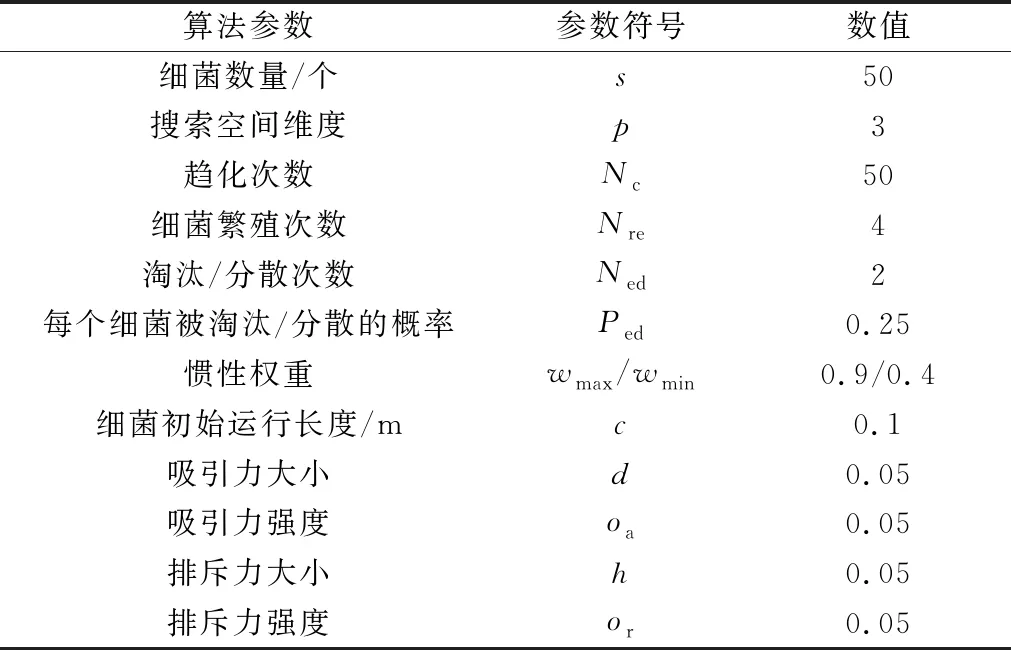
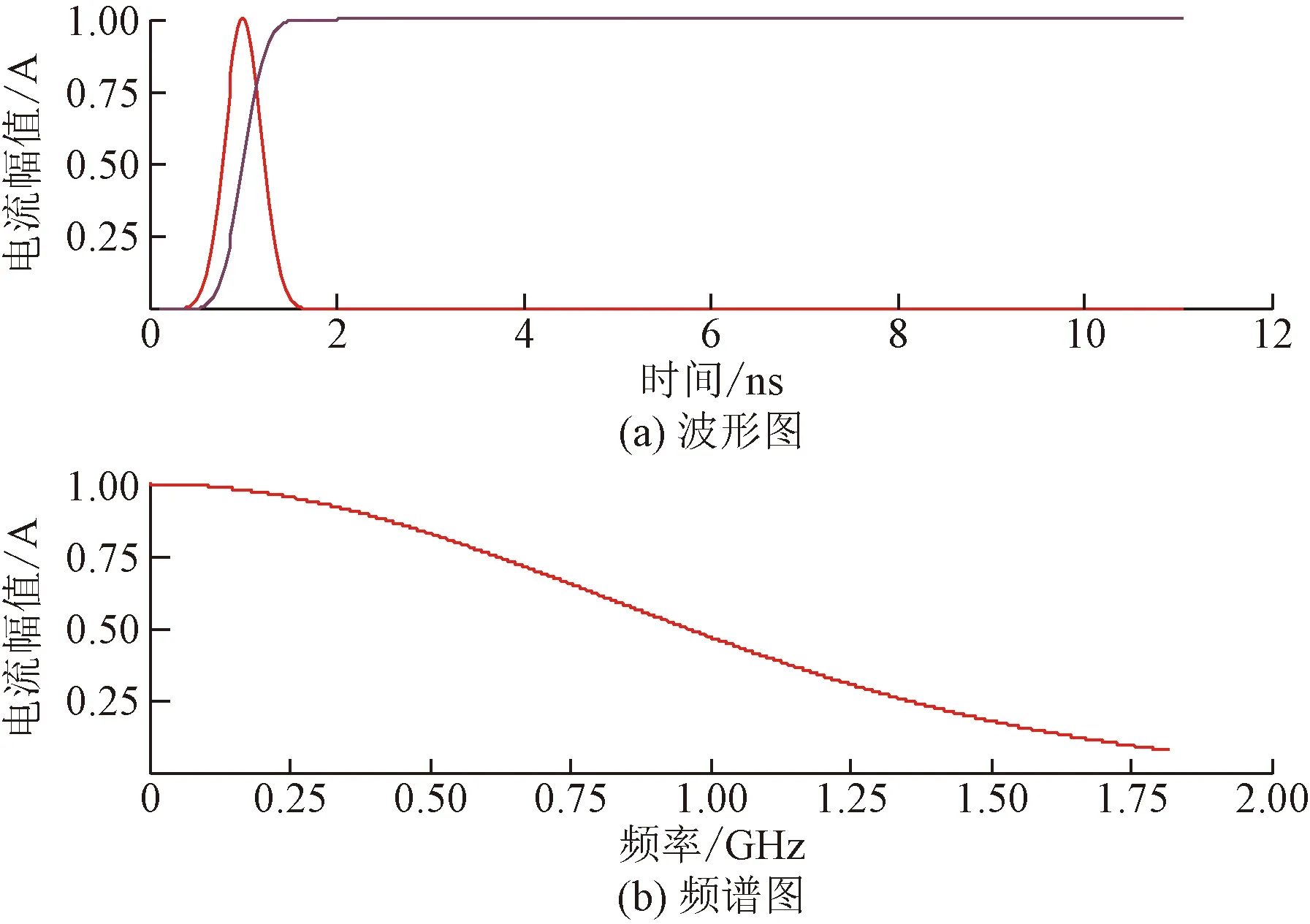
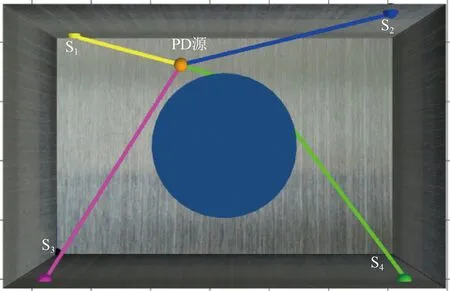
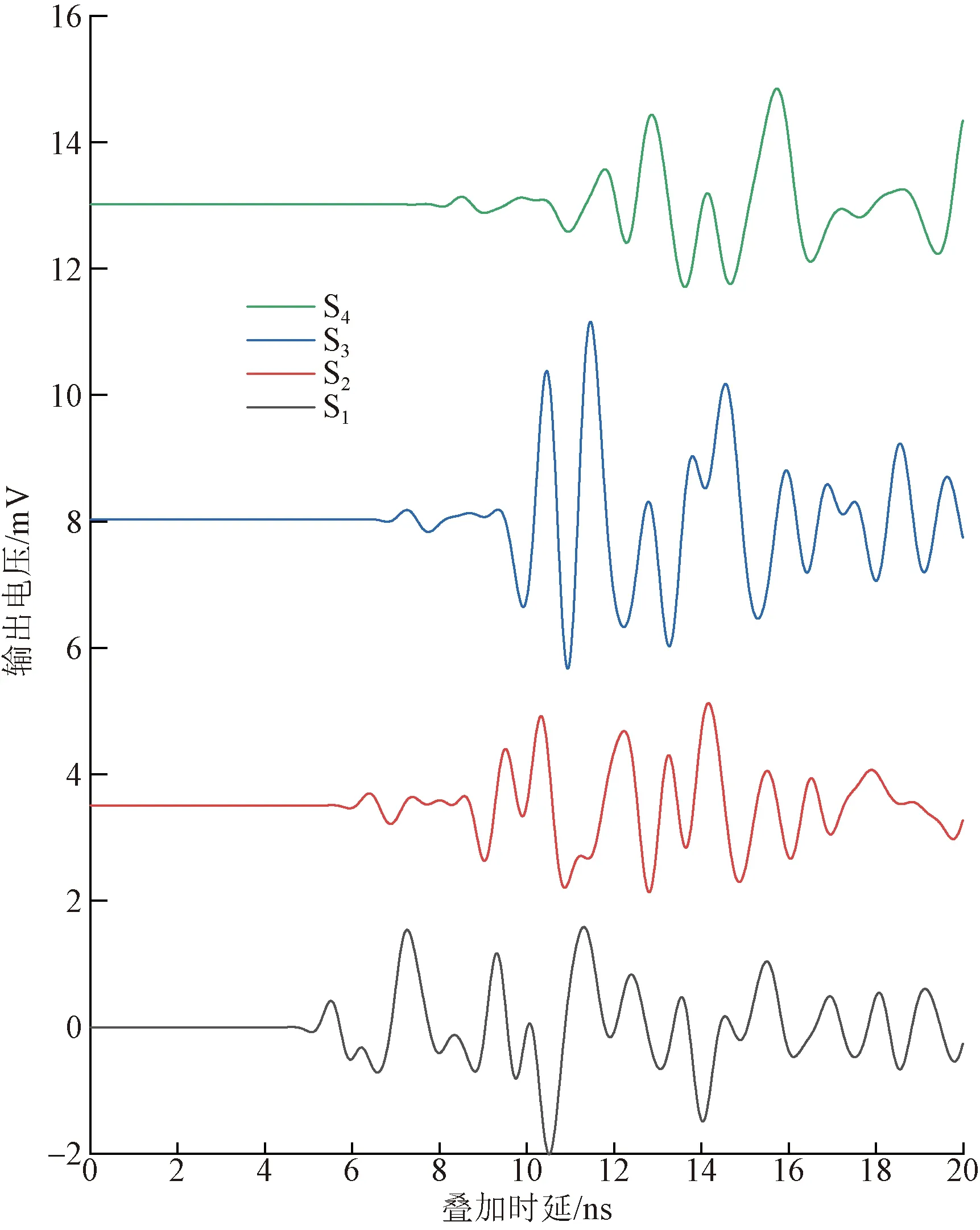
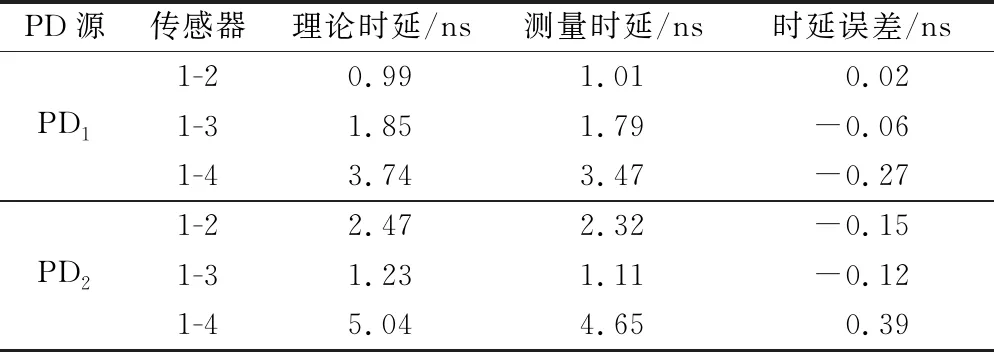
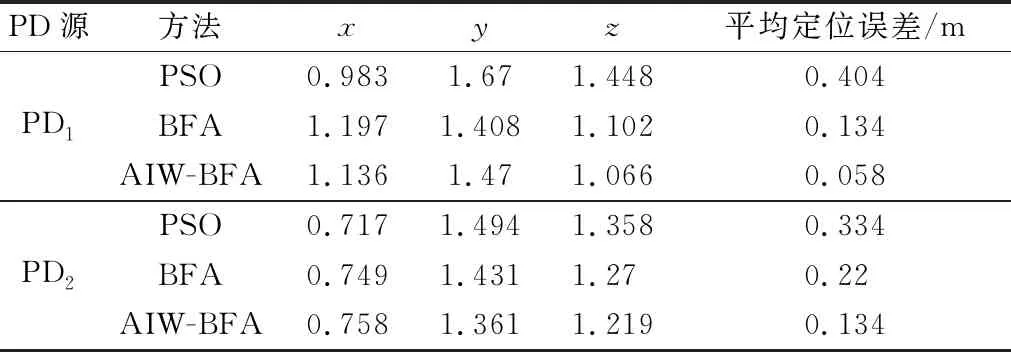
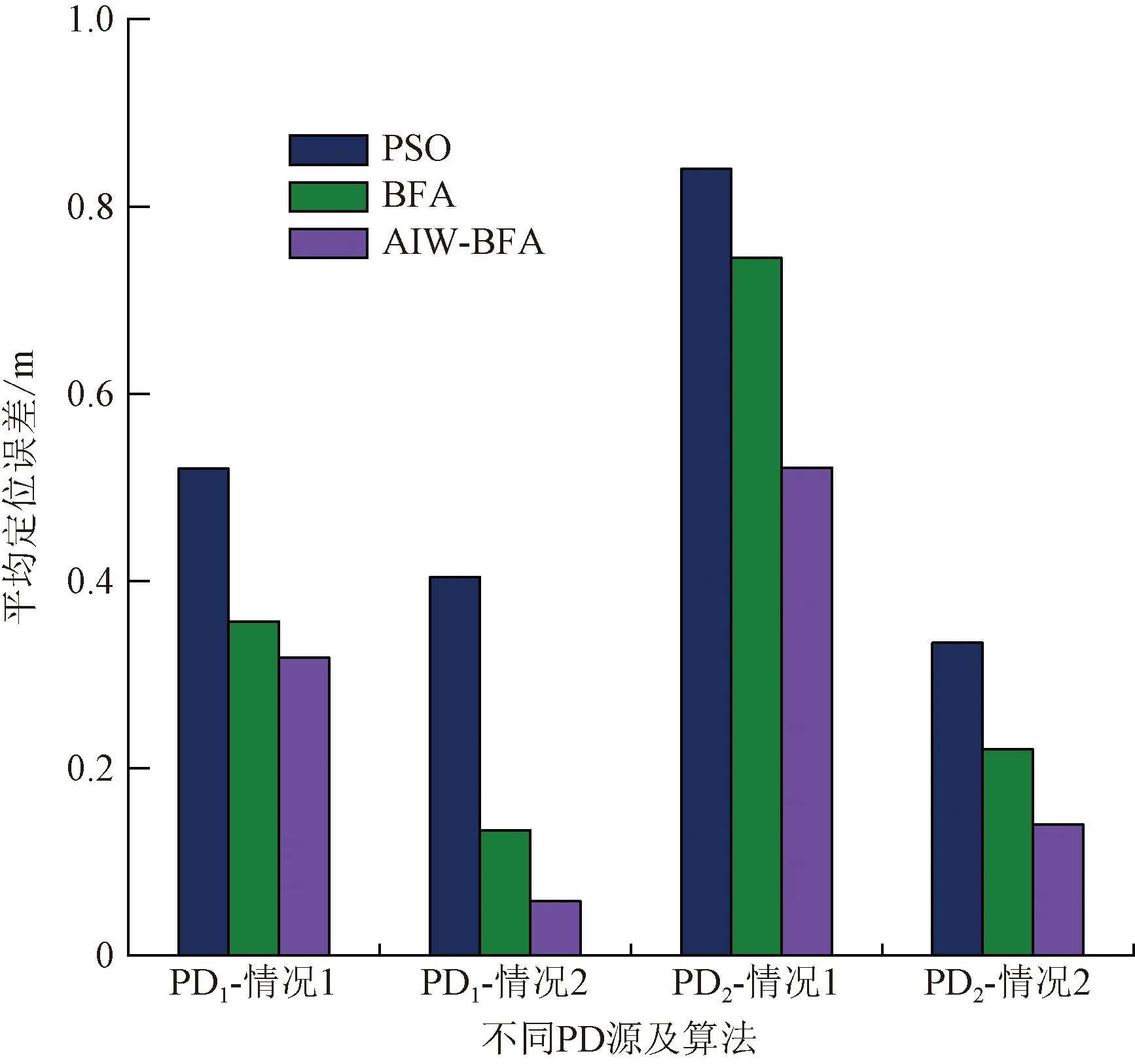
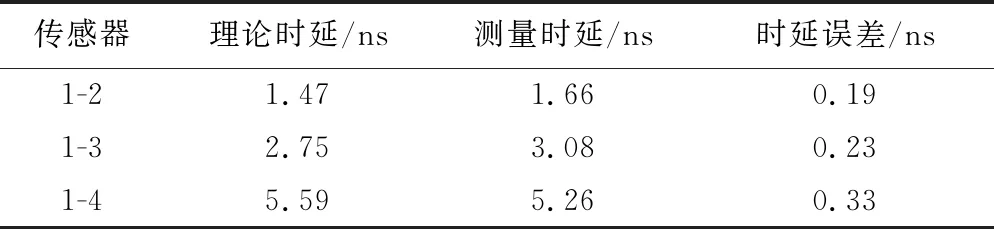
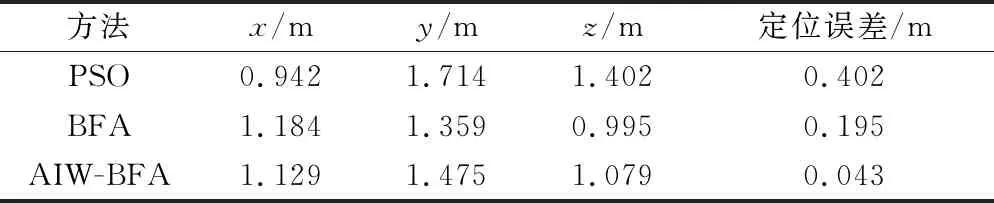
以二维平面中铁芯的圆心到PD源与传感器间的线段距离dn为判断依据,若dn (8) 结合式(3)与式(8),将目标函数表达为式(9),通过最小化目标函数来得到PD源的定位结果。 (9) 现有的常用方法中,BFA算法具有全局搜索寻优、不易陷入局部最优等优点,成为生物启发式计算研究领域的一个热点[20-21]。 BFA模型通过模拟细菌觅食的行为进行全局寻优求解。最优值即为目标函数的最小值。 步骤1首先,随机产生s个细菌,而每个细菌受到其他细菌的吸引排斥影响Jcc,则将目标函数[式(9)]转化为 (10) 式(10)中:d、oa、h、or分别为第i个细菌受到其他细菌的吸引力的大小和强度以及排斥力的大小和强度;Pi为第i个细菌经过j次趋化、k次复制(繁殖)、l次消除和分散过程后的位置。 (11) 步骤3趋化过程凸显了细菌的局部搜索寻优能力,复制过程能加快细菌的搜索速度。为了避免细菌陷入局部最优,BFA引入分散过程来实现全局寻优。 即细菌在完成一定次数的复制后,将以一定概率被随意分散到搜索空间。每个细菌都有Ped的概率被分散或者死亡,但同时会随机新生成与死亡细菌同等数量的细菌,保证解空间中细菌种群总数不变。然后再次回到步骤1和步骤2。 其中每个细菌的位置更新表达式为 (12) 式(12)中:ci(k)为第i个细菌第k次复制(繁殖)时的步长;Δi(k)为i个细菌向随机的单位向量方向进行翻转。 BFA算法中固定的游走步长并不能同时满足全局寻优与局部寻优,因此,引入一种自适应惯性权重w对游走步长进行改进,以动态适应问题的求解流程,表达式为 ci+1(k)=wci(k) (13) (14) (15) (16) AIW-BFA算法流程如下。 步骤1设置s个细菌,在搜索空间内产生随机的位置,初始化设置趋化次数Nc、繁殖次数Nre、淘汰/分散次数Ned。 步骤2每个细菌进行趋化过程,以式(12) 不断更新位置,以式(9) 和式(10)更新其对应的目标函数值Ji。 步骤4进行分散过程,以一定概率淘汰或分散细菌,同时保证细菌的总数不变,接着返回步骤2。 步骤5在迭代过程中,如果满足了算法收敛准则或迭代次数达到最大,则执行步骤 6。 步骤6输出细菌所对应的位置,即为最优解Pbest。 AIW-BFA算法的相关参数设置如表1所示,参数设置参考文献[22]。 表1 AIW-BFA算法参数设置表 利用Ansoft HFSS15.0 version建立仿真模型,评估AIW-BFA算法对局部放电源定位的有效性。构建2.83 m×1.82 m×1.88 m的变压器,与现场实验所用变压器大小相同,仿真采用脉冲电流的幅值为1 A,脉冲宽度为1 ns的高斯脉冲来模拟PD源[23],电流方向为z轴的正方向,脉冲电流的波形图及其频谱分析如图4所示。由于仿真过程是在真空环境下,因此v取3×108m/s。 图4 仿真用脉冲电流的波形及频谱 记4个传感器的位置坐标分别为(0.2,1.82,0.3)、(2.53,1.82,1.58)、(0.2,0,1.53)、(2.63,0,1.53) m。设置模拟PD源于(1.1, 1.5, 1.1) m和(0.8, 1.3, 1.1) m处。为方便观察,采用.NET Windows Presentation Foundation(.NET WPF)和Helix 3D进行简易建模。以PD1为例,变压器内PD源与传感器阵列的相对位置关系,以及PD源到各个传感器可能的传输路径如图5所示。 图5 有障碍时仿真模拟结构图(以PD1为例) HFSS仿真得到的PD1到各个传感器的电磁波波形如图6所示。 图6 PD源到各个传感器的电磁波波形图 由图5可以看出,PD1到传感器S1~S3之间并无障碍,因此电磁波信号可以直线传播到达,而PD1与传感器S4之间存在障碍,此时电磁波信号无法直线传播,因此需要采用提出的模型计算PD1到S4之间的路径距离。PD2与PD1同理。通过第一峰值法,得到PD1与PD2通过理论计算以及仿真得到的时延,如表2所示。 由表2可得,提出的模型计算得到的理论时延与仿真得到的测量时延接近,时延误差小于0.5 ns,考虑到采样率的影响,该误差在可接受范围内,证明了所提模型的有效性。采用AIW-BFA定位算法,并结合文中提出的模型采用PSO, BFA以及AIW-PFA算法分别运行10次,取10次定位结果的均值作为平均定位结果,其与真实PD源所在的位置的误差称为平均定位误差。上述算法所得到的定位结果如表3所示。 表2 PD源到各个传感器的时延表 通过表3可得, AIW-BFA算法中PD1的平均定位结果为(1.136, 1.470, 1.066) m,与实际PD1的位置在xyz轴分别相差(0.036, -0.03, -0.034) m,平均定位误差为0.058 m,而PSO法和BFA法的平均定位误差分别为0.355 m和0.134 m,可得AIW-BFA法优于PSO法和BFA法;同理,在PD2定位过程中,AIW-BFA法的平均定位误差为0.14 m,而PSO法和BFA法的平均定位误差分别为0.402 m和0.22 m,大于AIW-BFA的平均定位误差。由此可得AIW-BFA法优于PSO和BFA算法。 表3 不同算法结合计算模型的平均定位误差对比 为了体现计算模型的有效性,分别在PSO、BFA以及AIW-BFA等算法下进行验证,平均定位误差结果对比如图7所示,其中情况1表示未结合模型时各个定位算法得到的定位结果,情况2表示结合模型时各个定位算法得到的定位结果。由图7可得在PSO、BFA和AIW-BFA法定位实验中,在结合模型的情况下,平均定位误差均小于未结合模型的情况,得出计算模型在一定程度上可降低PD源的定位误差,验证了计算模型的有效性和可行性。 图7 不同情况下的平均定位结果误差对比图 为了充分测试提出算法的性能,在现场进行对PD源定位的测试。采用某110 kV的单相电力变压器作为实验对象,分别将4个特高频传感器安装于箱体上,如图8 (a)所示。并采用针型电极来模拟PD源,如图8(b)所示。实验中安装的特高频传感器带宽在0.3~1.5 GHz,高速模数转换器的采样率为1.5 千兆采样/s。以内部可安装的针形电极和环形电极来模拟PD源。由于实验在油中进行,v取2.018×108m/s。 图8 110 kV变压器实验平台和模拟PD源示意图 利用特高频传感器来采集PD源信号, PD源坐标设置为(1.1, 1.5, 1.1) m,传感器得到的脉冲波形如图9所示,记录PD源到各个传感器的时延与传感器S1间的时延差见表4。 图9 传感器接收波形图 表4中理论时延代表结合提出的模型所计算出的PD源到各个传感器的时延差;测量时延代表现场实验测量出来的时延差。时延误差可能由于噪声及采样率引起。可以发现理论时延与测量时延较为接近,其实延误差小于0.5 ns,证明了提出的计算模型的有效性和可行性。 表4 各个传感器相对距离及时差 根据不同传感器之间的时间差建立非线性方程组,利用提出的AIW-BFA算法结合提出的计算模型进行最优化求解,共运行10次取平均定位结果,并与BFA和PSO进行对比。平均定位结果如表5所示,其中定位误差为平均定位结果与真实PD源所在位置的直线距离。 表5 定位结果对比表 通过对比发现,AIW-BFA法的平均定位结果约为(1.13,1.48,1.08)m,最接近真实的PD源位置,定位误差约为0.04 m,通过表5可以对比出AIW-BFA法优于BFA法和PSO法。再次验证了所提方法的有效性。 为提高PD源定位精度,提出了基于TDOA的AIW-BFA定位算法,并引入特高频信号发出的电磁波在PD源与传感器间路径的计算模型。通过仿真和实验分析,得到以下结论。 (1)AIW-BFA定位算法通过驱化、复制和分散等过程,保留寻优结果好的细菌,淘汰寻优结果较差的细菌,并能够在搜索过程中自适应调整步长,能够在实现全局最优的同时满足局部最优,提高了定位精度。在仿真与现场实验中其定位误差均优于BFA法和PSO法的计算结果,表现出优越的性能。 (2)当有障碍物时,由于电磁波在变压器内传播会发生反射、折射和衍射会导致时延误差。提出了PD源到各个传感器间路径距离的计算模型,从而得到各个时延,其所得的理论时延,与仿真实验和现场实验所得的时延都较为吻合,验证了传播模型的有效性;AIW-BFA算法与提出的计算模型结合进行PD源定位,在仿真与现场实验中均表现良好,验证了该方法的有效性和可行性。 研究所涉及的为变压器内存在单个局部放电源的情况,后续将考虑对存在多个局部放电源的情况进行深入研究。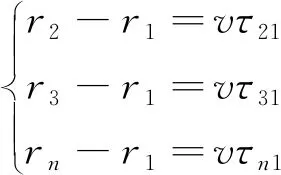
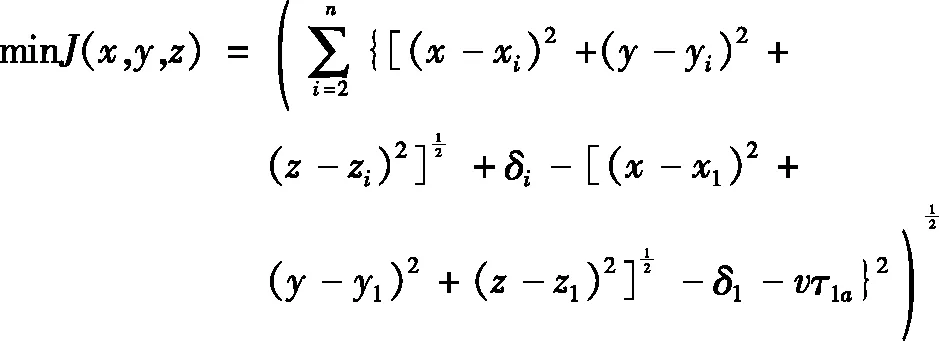
2 基于AIW-BFA的 PD源定位算法
2.1 BFA算法
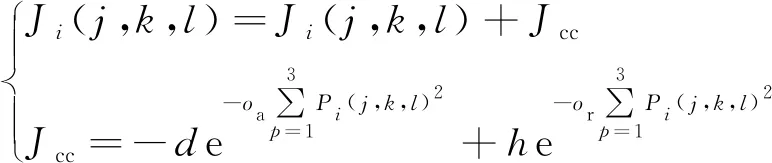
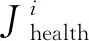
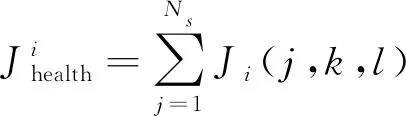
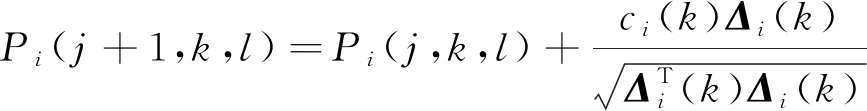
2.2 AIW-BFA定位方法
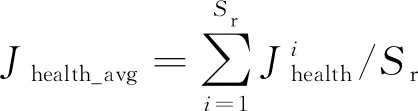
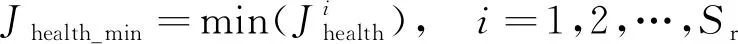
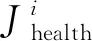
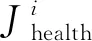
3 实验分析
3.1 仿真实验分析
3.2 现场实验分析


4 结论
