五自由度机械臂的建模与仿真

柳李琦， 李艳杰*， 卜春光

(1.沈阳理工大学机械工程学院， 沈阳 110159； 2. 中国科学院沈阳自动化研究所机器人学国家重点实验室， 沈阳 110016)

多关节的机械臂已有超过60年的历史，目前已广泛应用到工业领域，比较成熟的有ABB、KUKA等国外老牌企业生产的大型工业机械臂[1]等。随着机器人技术的发展和人们消费水平的提高，消费级的轻量型桌面级机械臂的应用越来越广泛，需求也愈加旺盛。

对机械臂进行运动学或动力学的仿真分析在机械臂的设计和应用阶段十分必要。唐雯雯等[2]对Dobot机械臂进行正运动学解析式，然后采用五次多项式插值法对机械臂进行了运动轨迹规划与验证，解决了高精度轻量型智能实训机械臂Dobot Magician的控制问题；赵修琪等[3]以5自由度自动镀膜机械臂为研究对象,运用改进D-H(Denavit-Hartenberg)法建立机械臂的运动学方程,并利用数值分析法对正、逆运动学方程进行分析求解。通过分析所得到的仿真结果表明,其规划路径与理想路径基本一致，所设计的5自由度自动镀膜机械臂可以满足微孔滤膜镀覆的工作要求；武洪恩等[4]使用UG和Adams软件对装车机器人的运动进行仿真，为机器人的运动控制及优化提供了参考。但上述中的路径仿真也只是停留在仿真阶段，缺少了在实际中的应用与验证。不论是设计还是仿真分析都只是简单的实验，缺少较深层次的研究与论证。

现设计一款五自由度桌面级机械臂，使用Solidworks软件完成其机械结构设计，完成基于D-H坐标法的正运动学理论建模；为了验证机械臂结构和运动学特性的合理性，通过Adams软件完成该机械臂虚拟样机的建立，然后构建Adams和MATLAB两者的模型，使其能够进行正确的联合仿真，并对机械臂的运动学性能进行分析，最后将仿真结构应用到实际中。整个过程不仅对上述文献研究进行更加详细、深入的探讨论证，还通过实验证明该研究的必要性和创新性。

1 五自由度机械臂的三维建模

设计的机械臂有5个自由度，分别是底座旋转、肩关节旋转带到大臂动作、肘关节旋转带动小臂动作、腕关节扭转和俯仰两个旋转作带动手爪动作，作为末端执行器的手爪可以完成开合动作。

各关节采用数字舵机驱动，为了既保持强度又减轻质量，舵机支架、大小臂都选用长条形铝合金薄板组成。

用Solidworks软件对机械臂进行了三维建模，如图1所示。

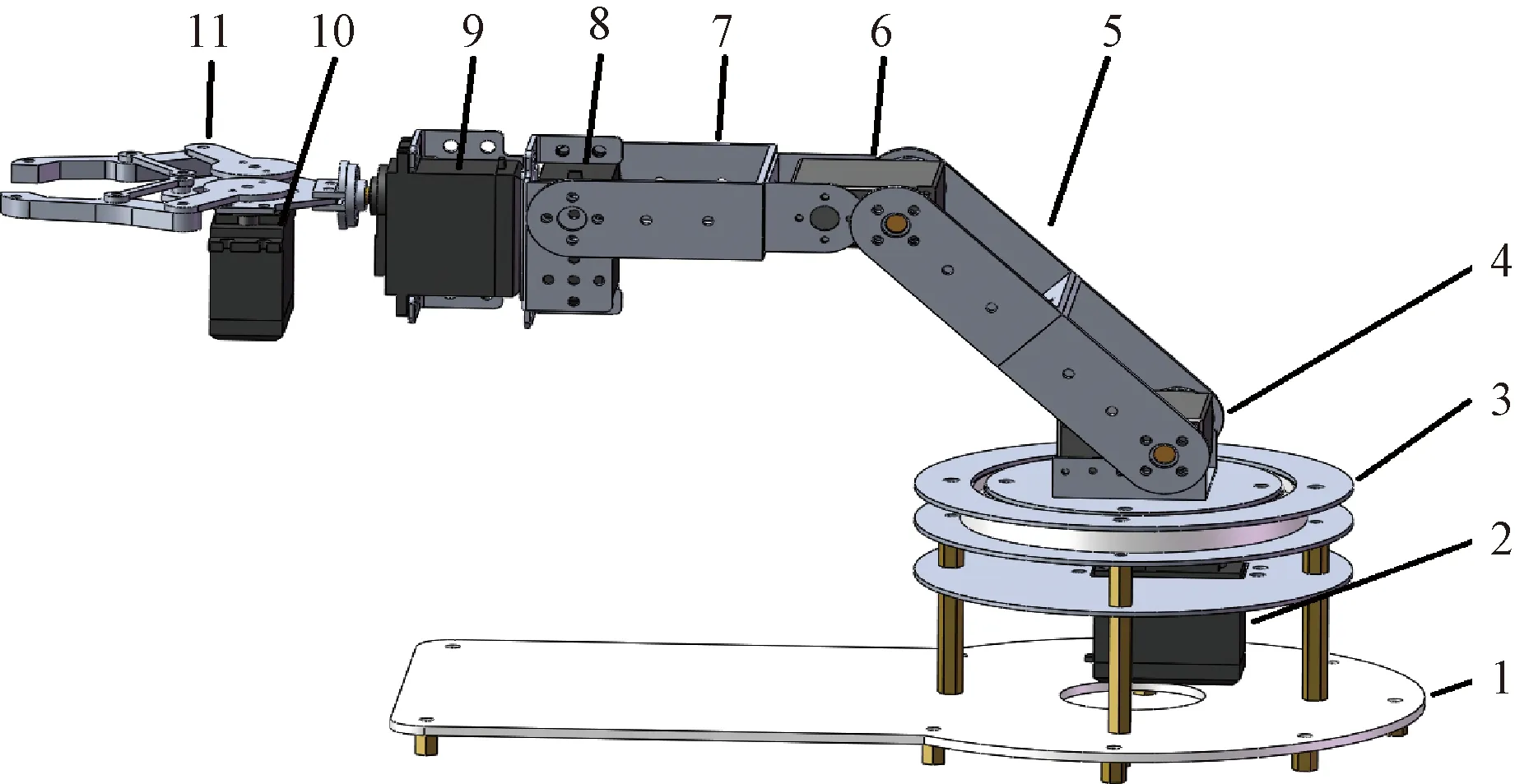
1为固定底板；2为底部旋转舵机；3为底座；4为肩关节舵机；5为大臂；6为肘关节舵机；7为小臂；8为腕关节俯仰舵机；9为腕关节扭转舵机；10为手爪开合舵机；11为机械手爪

2 五自由度机械臂的虚拟样机

为了更好地对机械臂进行运动分析，选用Adams软件，但Adams的建模技术还有很多不足。将在Solidworks软件中建立的物理模型导入Adams软件中，再进行运动学分析[5]。

2.1 模型的导入

在将Solidworks中的三维模型导入Adams之前应尽量简化模型中零件的数量，如螺钉、垫圈等不影响运动关系的小零件。

机械臂Solidworks与Adams软件的模型转换过程如下。

步骤1在Solidworks选项下拉菜单中找到插件这一项，然后打开将Solidworks Motion勾选。确定勾选后进入下一步。

步骤2点击底部的“运动算例”，选择“基本运动”下的“Motion分析”，再将键码往后拖至2 s，Motion分析选项旁的计算就可以执行了。接下来执行运动算例计算。完成后进入下一步。

步骤3找到模型并右键选择“输出到Adams”，注意保存的文件路径和文件名称不要出现中文。然后进入下一步。

步骤4找到保存的文件，可以看到其中有一个为***.adm，这个模型支持Adams直接打开。

步骤5启动Adams，选择现有模型，右键后选择浏览，找到该文件，该模型打开。

2.2 添加约束和驱动

为了构建虚拟样机并进行仿真分析，需要根据机械臂各部件之间的运动关系，在Adams模型中各关节连接处设置旋转副和施加关节驱动。该机械臂的5个关节均为旋转关节，故在模型的各舵机转轴处添加旋转副和转动驱动。

Adams具有一定的对模型进行自主检测的功能。使用该功能可以检查两个零部件之间存在的冗余或冲突等的相互关系，在模型自检正常后即可进行仿真分析。

3 基于Adams的五自由度机械臂仿真

3.1 五自由度机械臂的运动学正解

D-H坐标法是一种常用的机器人运动学建模方法，根据坐标系选取方法的不同，分为标准D-H方法和改进D-H方法[6]。用改进D-H方法建立该五自由度机械臂的D-H坐标图，如图2所示，相关D-H参数如表1所示。

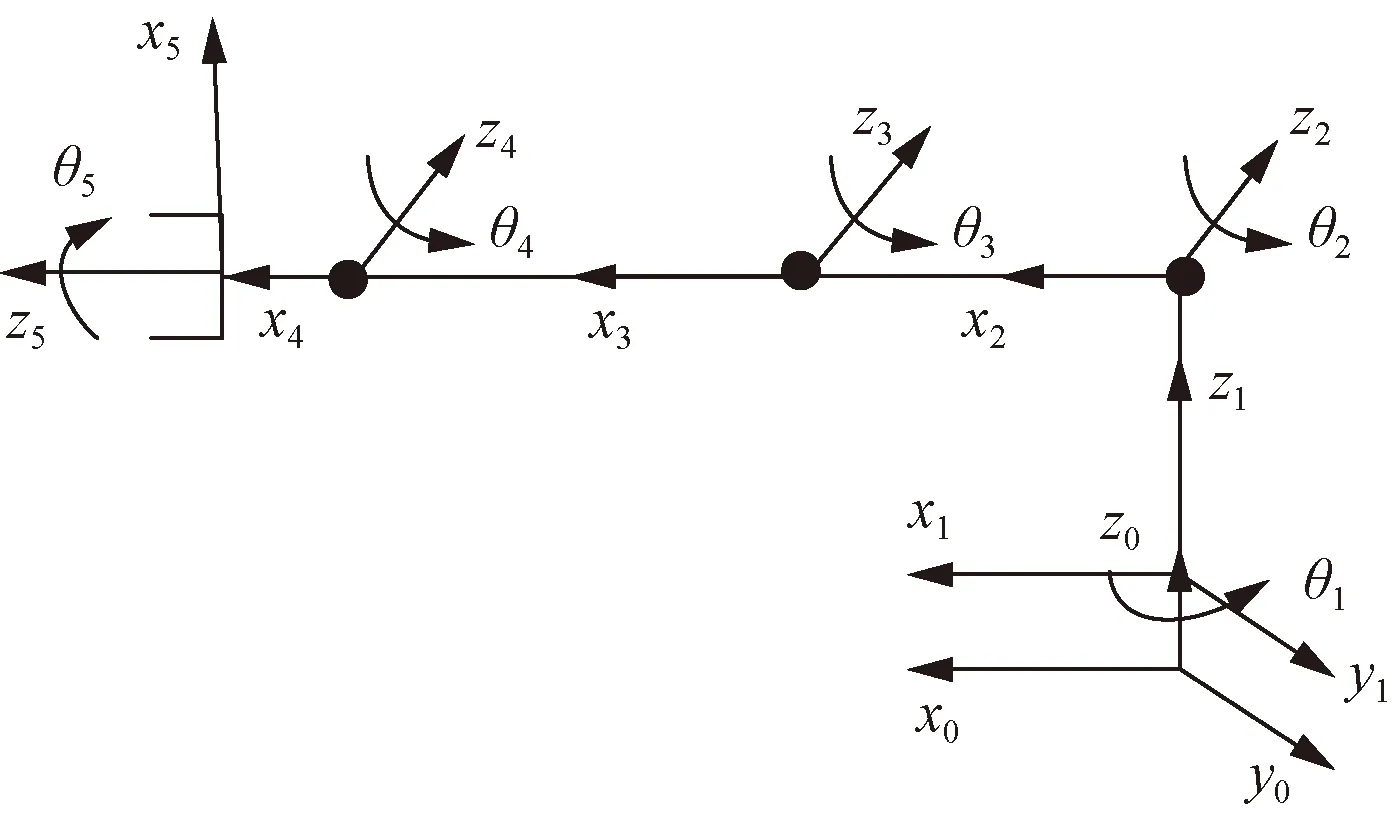
xi、yi、zi分别为第i轴坐标系的x、y、z轴；θi为以zi方向上，xi-1和xi间的夹角

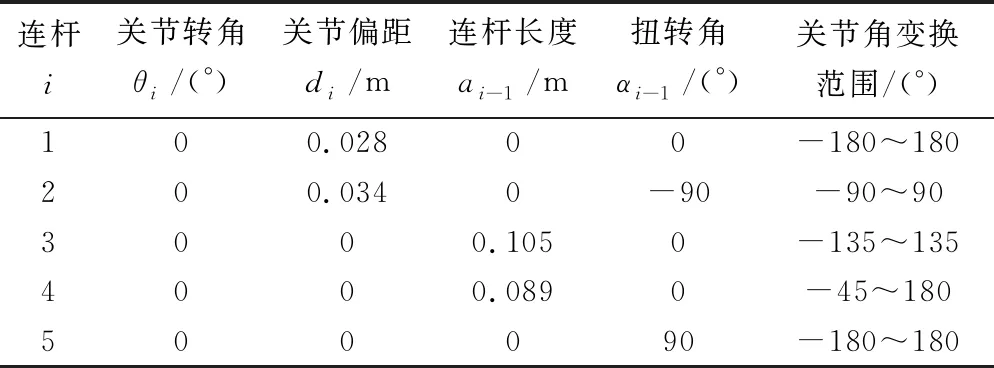
表1 五自由度机械臂的D-H参数表

根据改进D-H变换顺序得到杆件之间的转换关系式为

i-1Ti=

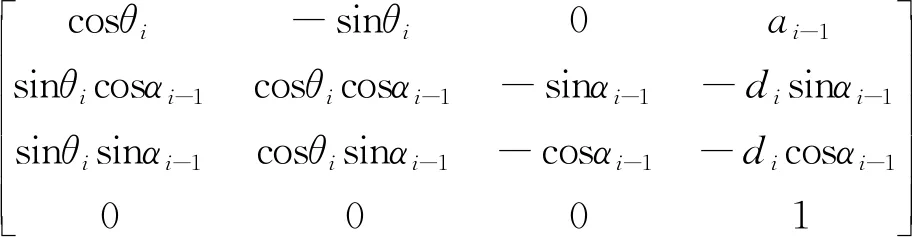
(1)

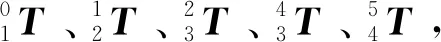
(2)

式(2)的4×4矩阵包含一个3×3矩阵、一个3×1向量和(0,0,0,1)。其中3×3矩阵表示末端执行点的位姿，用欧拉角表示；3×1向量为末端执行点的位置向量；(0,0,0,1)为常值。

式(2)表述了机械臂相对于基坐标系的末端空间位置与各个关节的变量和姿态之间的关系。合理地给定各个关节的运动状态，能够确定所需要机械臂末端的空间位置和姿态。

3.2 五自由度机械臂运动规划仿真

机械臂工作时有多种运动规划方法。目标空间位置相同，但采用了不同的运动规划算法，其运动速度、加速度等运动学特性不同。建立五次多项式插值轨迹规划算法模型，并进行运动学仿真计算，考察机械臂末端运动的平稳性。为了便于算法实现，使用了Adams的动力学及运动学仿真的环境并且充分利用MATLAB的强大计算功能、极高的编程效率这一优势，对机械臂的运动规划等进行联合仿真。

3.2.1 五次多项次规划算法

使用的机械臂运动规划轨迹是五次多项式函数，该函数是一个时间的函数，其最重要的特性就是光滑性。机械的运动特性一般要求位置、速度和加速度是光滑连续的，因而，如果初始点和终点均限定位置、速度、加速度3个条件，可以使用确定的五次多项式进行机械臂关节的轨迹规划。

设初始时刻t0和终止时刻tf的角位置、角速度和角加速度分别满足式(3)和式(4)，即

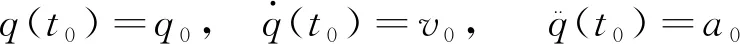
(3)

(4)

式中：q0、t0、a0分别为初始时刻的位移、速度和加速度；qf、tf、af分别为终止时刻的位移、速度和加速度。

任意时刻轨迹满足式(5)所示的五次多项式，即

q(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5

(5)

式(5)中：a0～a5为五次多项式的系数。

根据式(3)和式(4)的已知条件，并将式(5)求取一阶导数和二阶导数后，可以得到如式(6)所示的方程组。

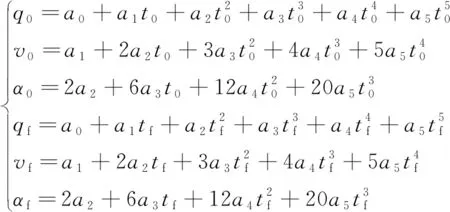
(6)

通过式(6)可以求得五次多项式的6个待定系数ai(i=0,1,…,5)，进而得到期望的角度、角速度和角加速度分别为

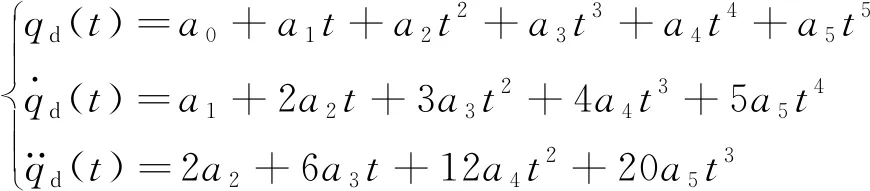
(7)

3.2.2 机械臂的运动规划联合仿真

在Adams的“单元”模块中设置并确定该机械臂系统输入量和输出量，在“控制”插件中点击“机械系统导出”功能项，选择导出至MATLAB软件，选择非线性分析，在“解算器”中选择“C++”，点击确定，即获得在MATLAB Simulink直接使用的子模块“adams_sub”,该模块可以在Adams和MATLAB之间实时进行数据传递[7-9]。

假设各关节的初始角速度与初始角加速度均为0，终止角速度与终止角加速度也是0，设置终止时间tf为20 s，五次多项式的规划算法如下[10-11]。

function [qd,dqd,ddqd] = fcn(q0,qf,t)

%q0为初始位置，qf为终止位置

q01=q0(1);qf1=qf(1);tf=20;

a10=q01;

a13=(10*qf1-10*q01)/tf^3;

a14=(15*q01-15*qf1)/tf^4;

a15=(6*qf1-6*q01)/tf^5;

qd=a10+a13*t^3+a14*t^4+a15*t^5;%规划路径

dqd=3*a13*t^2+4*a14*t^3+5*a15*t^4;%规划角速度

ddqd=6*a13*t+12*a14*t^2+20*a15*t^3;%规划角加速度

假设连杆2和3在tf时间内进行一次各自关节变换范围内的运动。取关节二的仿真运动方向为0°～45°；关节三的仿真运动方向为0°～90°。Adams_sub的输出为该关节的仿真角位置、角速度和角加速度，并在联合仿真模型中分别与规划路径、规划角速度和规划加速度进行对比。建立的Adams和MATLAB的联合仿真模型如图3所示。

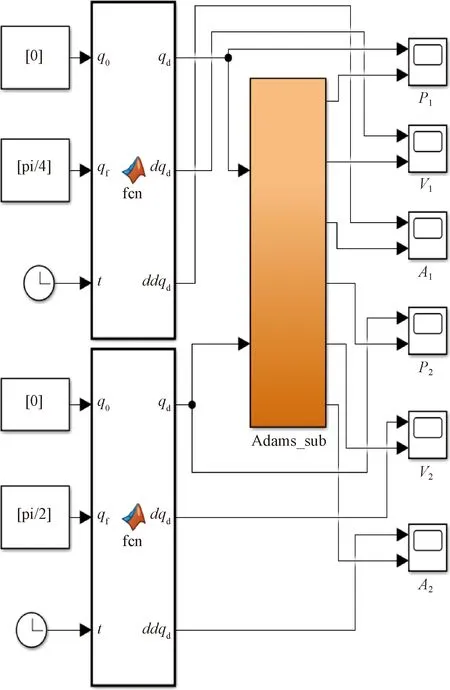
P1、P2分别为关节一、二的角位移；V1、V2分别为关节一、二的角速度；A1、A2分别为关节一、二的角加速度；pi表示圆周率π

如图4所示是Adams下虚拟样机导入MATLAB/Simulink生成的仿真子模型Adams_sub。子模型中左侧的3个输入分别为虚拟样机中关节二、三、四的驱动指令，选用五次多项式规划路径；输出分别为虚拟样机中关节二、三、四的仿真路径、仿真角速度和仿真角加速度。

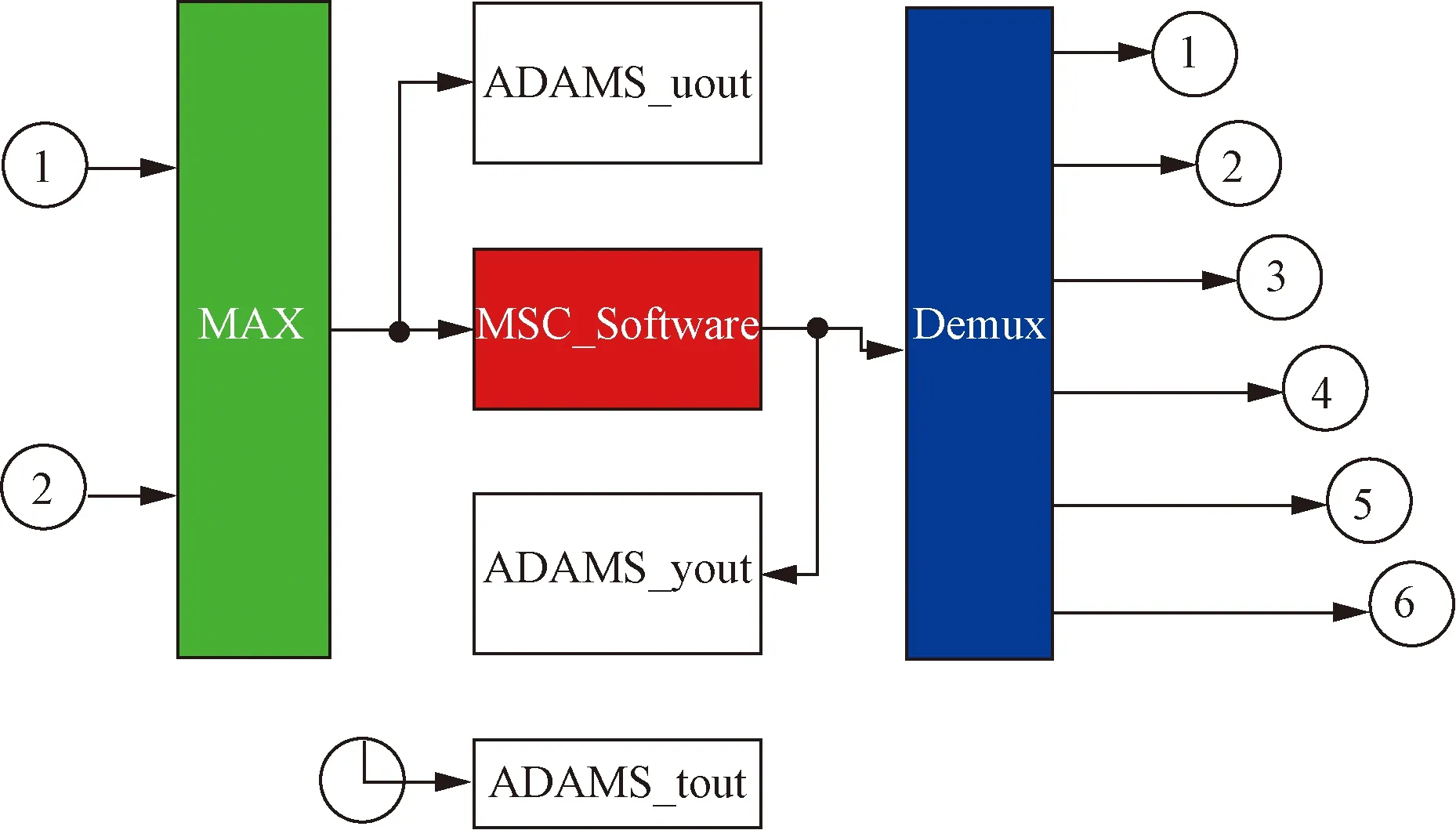
MAX为多路复用器；ADAMS_uout为U工作区；MSC_Software为MSC软件；ADAMS_yout为Y工作区；ADAMS_tout为T工作区；Demux为多路分配器

图5～图10所示分别为关节二和关节三的规划路径和仿真路径对比图、规划速度和仿真速度对比图以及规划加速度和仿真加速度对比图。可以看出，虚拟样机的仿真路径、速度和加速度运动曲线与规划曲线基本一致。该结果验证了机械臂能够在工作空间内实现规划运动，运动学特性稳定。

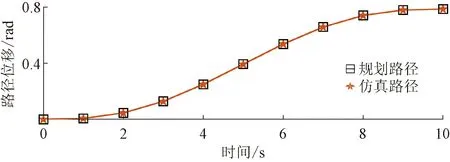
图5 关节二规划路径与仿真路径对比图

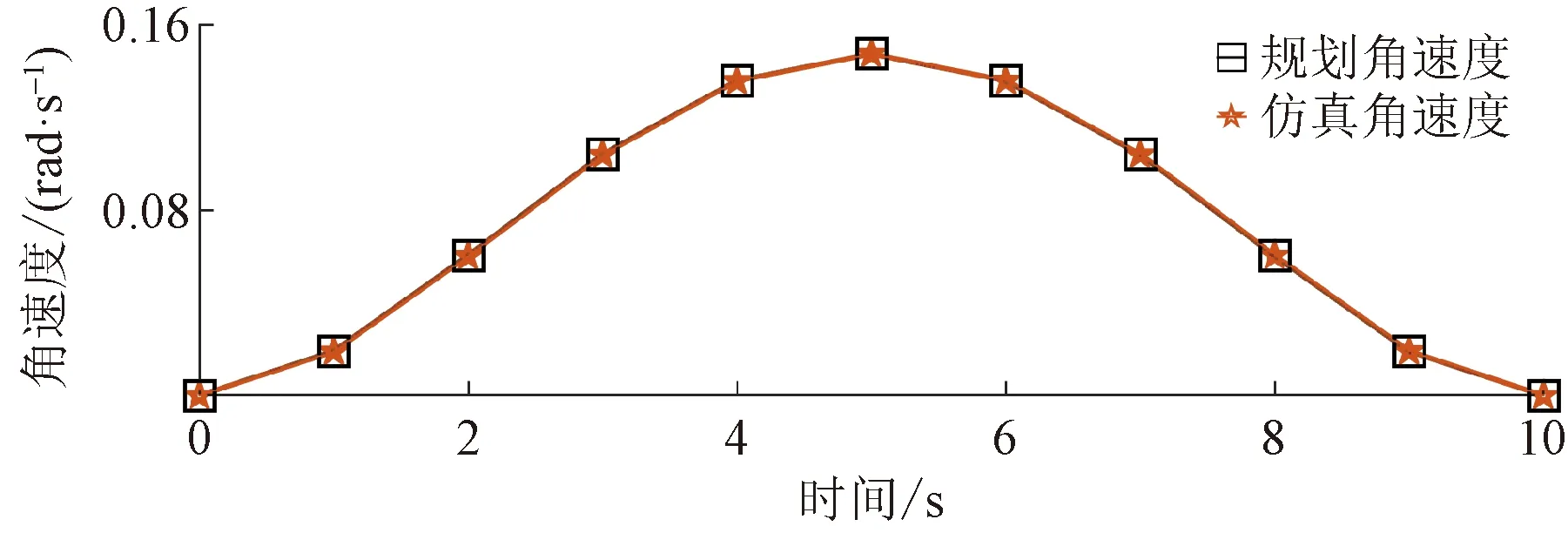
图6 关节二规划角速度与仿真角速度对比图

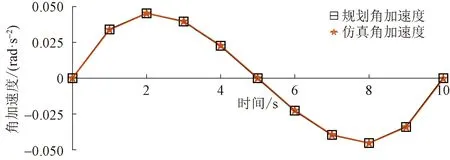
图7 关节二规划角加速度与仿真角加速度对比图

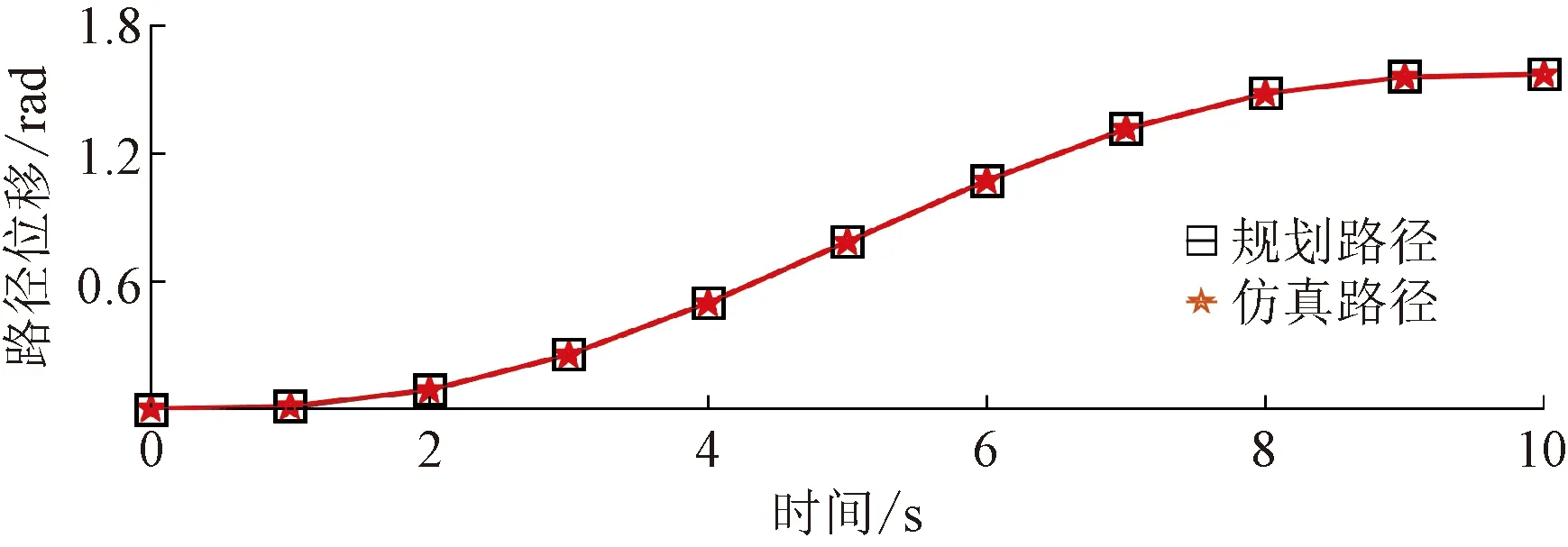
图8 关节三规划路径与仿真路径对比图

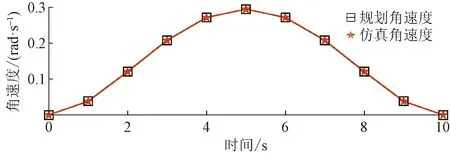
图9 关节三规划角速度与仿真角速度对比图

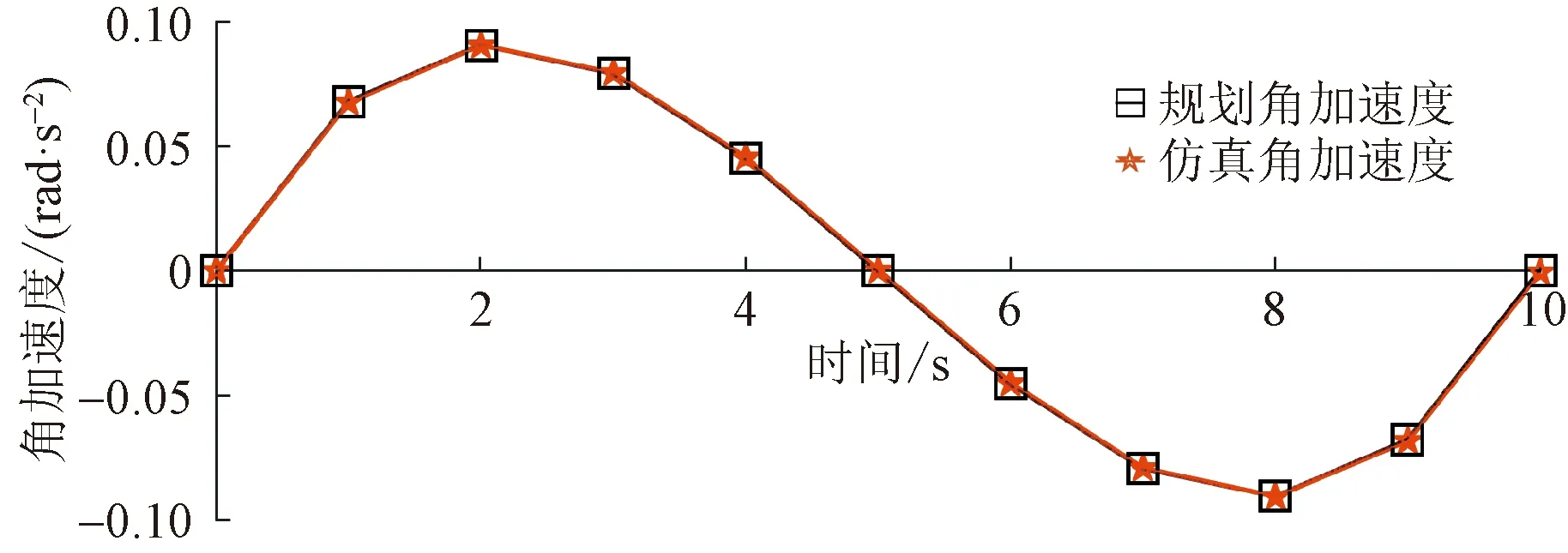
图10 关节三规划角加速度与仿真角加速度对比图

图11～图13所示分别为机械臂末端空间位置、速度及加速度的曲线图。取机械臂的关节二处的舵机中心为初始坐标，机械爪的爪中心处为终止坐标，可得到该机械臂末端在仿真过程中的相对空间位置、速度及加速度曲线，即3个关节的总运动特性。仿真结果表明，机械臂末端运动特性连续、光滑，可实现平稳作业。

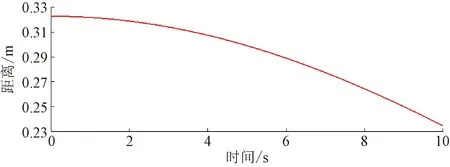
图11 机械臂末端空间相对位置曲线图

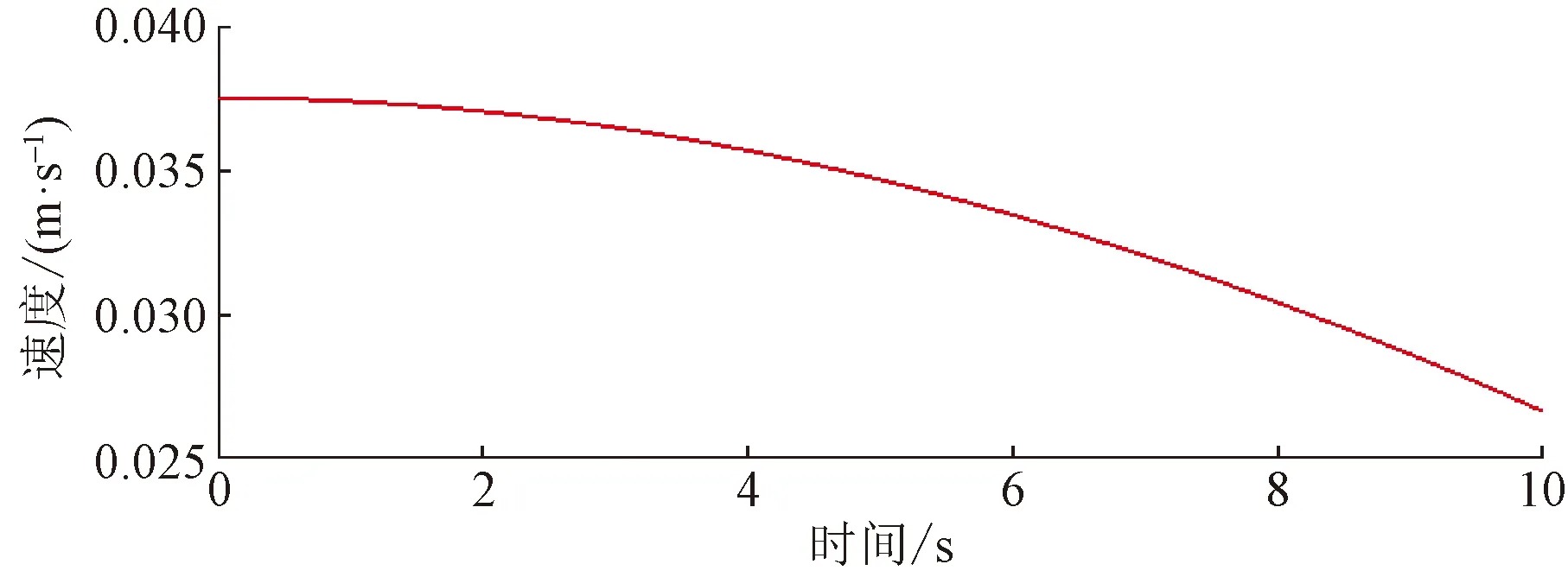
图12 机械臂末端空间相对速度曲线图

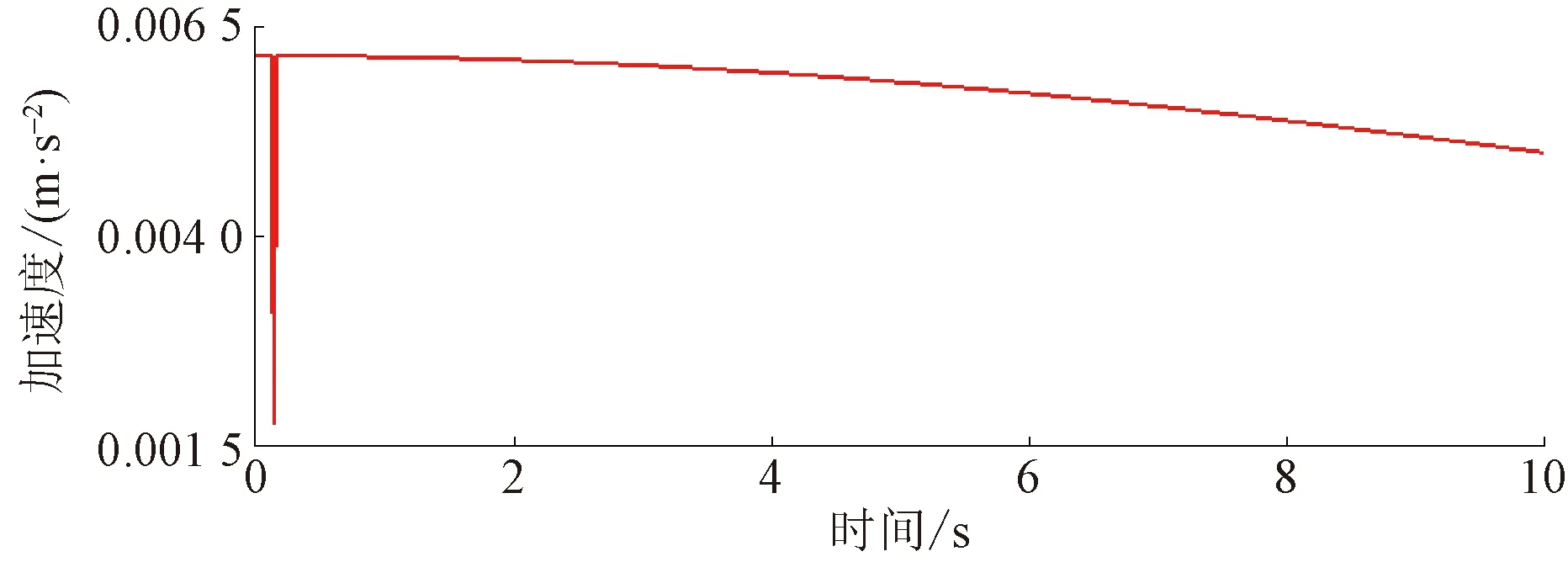
图13 机械臂末端空间相对加速度曲线图

参考上述的五次多项式路径规划，将该技术应用到机械臂拾取物品的放置到收纳盒的仿真实验。

图14所示分别为该机械臂在Adams中将物体转移至收纳盒的仿真实验，图14(a)～图14(e)分别为仿真过程中在不同时刻的虚拟样机位姿图。其中图14(a)为机械臂、物体和收纳盒的初始相对空间位姿示意图；图14(b)为机械臂对物体进行相对运动的示意图；图14(c)为机械臂对物体施加作用力，进行抓取的示意图；图14(d)为机械臂携带物体相对收纳盒进行空间位置运动示意图；图14(e)为机械臂将物体投入至收纳盒的示意图。联合仿真结果表明，机械臂结构设计合理，可实现光滑平稳运动，运动学特性良好。

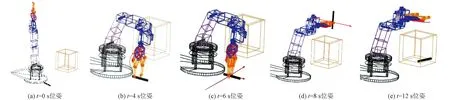
图14 虚拟样机位姿图

4 机械臂制作与应用

设计的桌面级五自由度机械臂实物图如图15所示。该机械臂采用经表面喷砂处理过的全铝合金机体，用U形支架组合成大臂和小臂，关节驱动使用防堵功能的数字舵机。

图15 桌面级五自由度机械臂实物图

图16所示为该机械臂按照上述的五次规划路径进行的夹取、转移中性笔的实际运动。实验表明该机械臂的运动具有上述的五次多项式运动特性，并且能够较好地完成夹取、转移中性笔的作业。

图16 机械臂的位姿图

5 结论

设计了一款桌面级五自由度机械臂，基于D-H坐标法给出了机械臂的运动学数学模型，建立了该机械臂的虚拟样机，并实现了与MATLAB的联合仿真，仿真结果验证了机械臂结构设计的合理性，机械臂能实现平稳运动，运动学特性良好。

建模与仿真分析为该机械臂的真实样机制作与应用操作奠定了基础，也为对机械臂后续控制算法验证等提供了虚拟实验条件。