水力压裂多裂缝扩展的近场动力学模拟

曹楷楠， 胡志明， 端祥刚， 常进

(1.中国科学院大学工程科学学院， 北京 100049； 2. 中国科学院渗流流体力学研究所， 廊坊 065007； 3.中国石油勘探开发研究院， 北京 100083)

为了解决水力压裂裂缝起裂与扩展中的力学问题，一般采用理论分析、实验方法和数值模拟方法。常用的数值模拟方法包括有限元方法、边界元法、扩展有限元方法等[1]，是基于连续介质力学理论，将裂缝的扩展看作裂缝内压裂液流动和岩体断裂变形的耦合问题。连续介质理论假设物质点只和相邻的物质点有相互作用，近场动力学基于非局部理论，即物质点和近场范围内的所有物质点均有相互作用，以积分方程代替微分方程，不需要空间求导，便于处理材料裂纹扩展中的不连续问题。Agwai等[2]将宏观上描述裂纹扩展的扩展有限元方法(extend finite element method，XFEM)与近场动力学(peridynamics，PD)做比较，结果发现近场动力学得到的结果与实验结果更接近，可以看到分叉行为与微观分叉行为。

近场动力学由Silling[3]提出，以位移的空间积分形式重构了传统连续介质理论，这种积分形式实现了对连续介质和非连续介质的统一描述，因此，近场动力学能很方便地描述材料中裂纹萌生和扩展。近场动力学尺度介于分子尺度与宏观尺度之间，兼具分子动力学和宏观连续介质力学的优势。分子动力学可以处理宏观尺度下的不连续问题，但是却难以实现大尺度的仿真预测，近场动力学可以弥补这一缺点[4]。

近场动力学目前广泛应用于材料的断裂及裂纹扩展预测上，在水力压裂裂缝扩展的问题上应用较少。页岩储层水力压裂裂缝扩展问题为裂缝内流体流动与岩石固体变形的流固耦合问题。中外研究人员借助近场动力学研究了水力压裂中的流固耦合问题，Turner[5]基于近场动力学建立了多孔介质渗流过程的流固耦合模型。吴凡等[6]通过键基的近场动力学理论，采用等效压力解决流固耦合问题，建立了二维的水力压裂模型；张钰彬等[7]通过常规态基的近场动力学理论，建立了平面二维的水力压裂模型。Ouchi等[8]基于常规态基近场动力学，建立了水力压裂模型，对水力裂缝与天然裂缝的相互作用进行了较为详细的研究。Nadimi等[9]通过近场动力学理论较为详细地研究了水力裂缝与天然裂缝的交互作用，并对排量等施工参数的影响进行不同结果的比较。Qin等[10]提出一种新的近场动力学模型和方法用于解决水力压裂问题。Zhou等[11]建立了近场动力学的流固耦合模型，应用到水力压裂问题中。近场动力学理论用于水力压裂的优势在于，通过描述物质点之间键的连接情况，可以自动捕捉到裂纹的扩展，不足之处在于物质点之间的间距有限制，不适用于大尺度仿真，通过耦合有限元方法可以解决这一问题[12]。

水平井技术和水力压裂技术是目前页岩气开发的主要技术手段，目的在于形成复杂缝网，提高页岩气采出程度。在页岩气的压裂过程中，通常要进行多簇射孔和多簇压裂，裂缝间会存在干扰，中外对多裂缝干扰问题的研究方法大多采用基于扩展有限元法及位移不连续法等[13-15]，现以水力压裂问题为研究背景，基于近场动力学理论，设计水力压裂多裂缝扩展的数值算例，预期从非局部理论的角度得到对多裂缝扩展规律的认识。

1 近场动力学运动方程及数值离散

Silling等[16]在键基近场动力学理论的基础上，提出态基近场动力学理论，可以更好地描述物体的变形。态基近场动力学的运动方程一般可以表示为

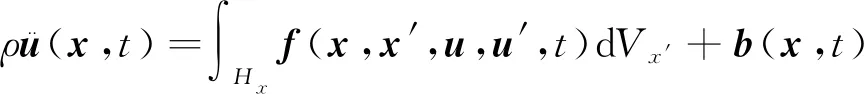
(1)

f=T[x,t]〈x′-x〉-T[x′,t]〈x-x′〉

(2)

式中：ρ为材料密度；x为物质点的位置矢量；u(x,t)为物质点位移；Hx为点x的近场范围；f为物质点之间的相互作用力函数，称为本构力函数；T[x,t]为力态；b(x,t)为体力；Vx′为邻点体积。近场动力学通过键的拉伸破坏描述物体的损伤和断裂，采用伸长率s表征键的拉伸程度，表达式为

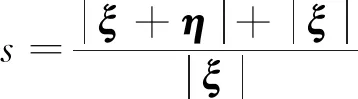
(3)

式(3)中：ξ为键长；η为相对位移。当伸长率大于临界伸长率s0时，键断裂，对于平面应力问题[17]，有

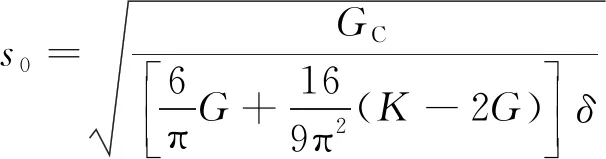
(4)

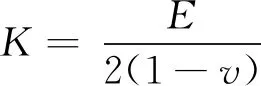
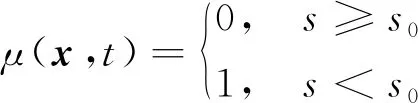
(5)

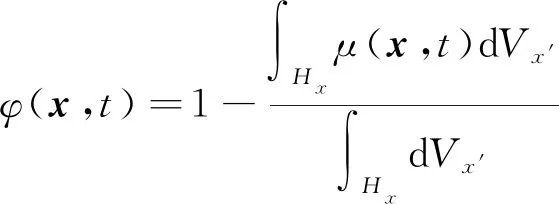
(6)

采用无网格方法直接离散得到物质点运动方程的空间离散化形式为

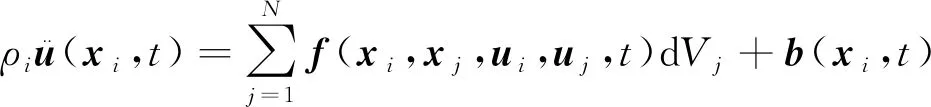
(7)

对于时间离散采用Velocity-Verlet方法，该方法相较于直接向前差分法，有较好的稳定性。该方法采用的积分形式为

(8)

2 流固耦合方法

2.1 固体域变形描述

对固体域直接采用近场动力学运动方程的离散形式，离散为一系列物质点，物质点存储位移，质量密度，体力密度等物理量信息。

对流体域，基于连续介质力学观点建立渗流控制方程，采用有限差分法进行离散，固体域和流体域共用同一套离散网格点，并依据有效应力原理，将裂缝和孔隙中的水压力添加到固体域物质点间的力态中，实现流固耦合过程。

Biot[18]引入有效应力系数，将有效应力原理应用范围由土力学扩展到岩土力学。对于多孔介质的有效应力，可以表示为

σtotal=σeff+αPI

(9)

式(9)中：σtotal为总应力张量；σeff为有效应力张量；α为Biot固结系数；P为孔隙压力；I为单位张量。通过损伤值大小划分连续空间，损伤无断裂空间与损伤断裂空间，分别对应3种键的力态。

(1)无损伤连续空间连续键力态。无损伤连续空间中物质点对之间的键未断裂，即物质点的损伤值为0，在平面应力问题的力态基础上[19]，得到物质点连接键上的力态为

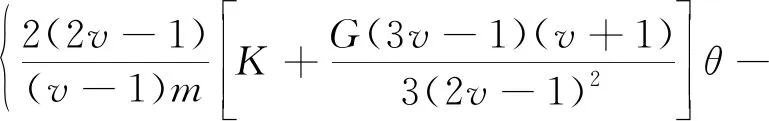
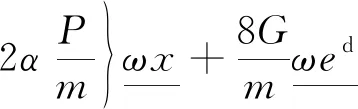
(10)

(2)损伤无断裂空间断裂键力态。当物质点对之间发生损伤，但是物质点损伤值没有超过临界损伤程度时，物质点处于损伤无断裂空间，物质点之间的力学项消失，但是孔隙压力项仍然保留，物质点之间的断裂键上的力态为

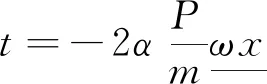
(11)

(3)损伤断裂空间的断裂键力态。将损伤值及邻对点损伤值均超过临界损伤值，且键为拉长状态的物质点作为损伤断裂空间的物质点[20]，将水力压力以非局部形式作用在物质点上，则损伤断裂空间的物质点之间的断裂键上的力态为

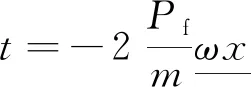
(12)

式(12)中：Pf为压裂液在裂缝面上的压力。

2.2 流体域压力描述

将流体域划分为裂隙区、基质区及过渡区，对应固体域变形描述中的损伤断裂空间，无损伤连续空间及损伤无断裂空间。

对于裂隙区的物质点，认为压力值近似为注入压力。对于基质区和过渡区的物质点，采用连续介质观点描述流体流动，物质点流动规律采用达西定律描述为

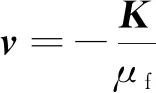
(13)

式(13)中：P为压力；μf为流体黏度；K为渗透率张量；对于各向同性的连续空间采用基质渗透率Kr、损伤断裂空间采用裂隙渗透率Kf和损伤无断裂空间渗透率Ks通过损伤程度取平均值获得，即

Ks=φKf+(1-φ)Kr

(14)

式(14)中：φ为物质点的损伤值。对于均匀各向同性介质，假设基质孔隙度不变，得到渗流控制方程[21]简化后的结果为

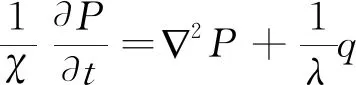
(15)

对于式(15)的控制方程，采用有限差分法对压力项和源项进行离散，采用显式差分格式对时间项离散，控制方程中的参数K、φ、ci、μf均为常数，于是得到二维直角坐标下离散后的控制方程为

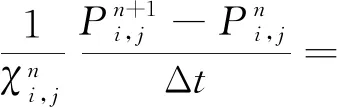
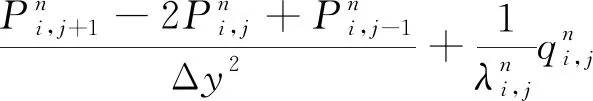
(16)

最后，借助C++工具和OpenMP并行框架实现流固耦合过程。

3 研究内容

3.1 模型及参数

设置模型尺寸为1.0 m×1.0 m，计算域内共划分10 000个物质点，其中水平方向和竖直方向分别划分100个物质点，物质点间距为0.01 m，近场范围取物质点间距的3倍，为0.03 m，边界厚度取近场范围大小，岩石弹性模量为5 GPa，岩石泊松比为0.333，岩石密度为3 400 kg/m3，流体密度为1 000 kg/m3，裂隙渗透率为1.333×10-3mD，基质渗透率为1×10-12mD，岩石材料孔隙度为0.5，Biot固结系数为0.5，综合压缩系数为1，将临界损伤程度设置为0.39[10]，即认为当物质点和相邻物质点的损伤程度均大于0.39时，物质点和相邻物质点位于裂缝的两侧，时间步长取0.000 001 s。模型边界设置为位移约束，边界四周固定，压力边界设置为透水边界，边界处压力为零。设置裂缝中心为压力注入点，预置裂缝内压力随时间匀速增加，压力增速为10 000 MPa/s。

为了研究缝间的干扰作用对多裂缝扩展规律的影响，设计了如图1所示的4组数值模型实验，其中，图1(a)为间距0.1 m的两条平行对齐裂缝，两条裂缝长度为0.1 m；图1(b)为间距0.2 m的两条平行对齐裂缝，与图1(a)对比，观察不同裂缝间距下的结果；图1(c)为两条平行交错裂缝，两条裂缝间距为0.1 m，两条裂缝长度为0.1 m；图1(d)为三条平行对齐裂缝，裂缝间距为0.2 m，裂缝长度为0.1 m。

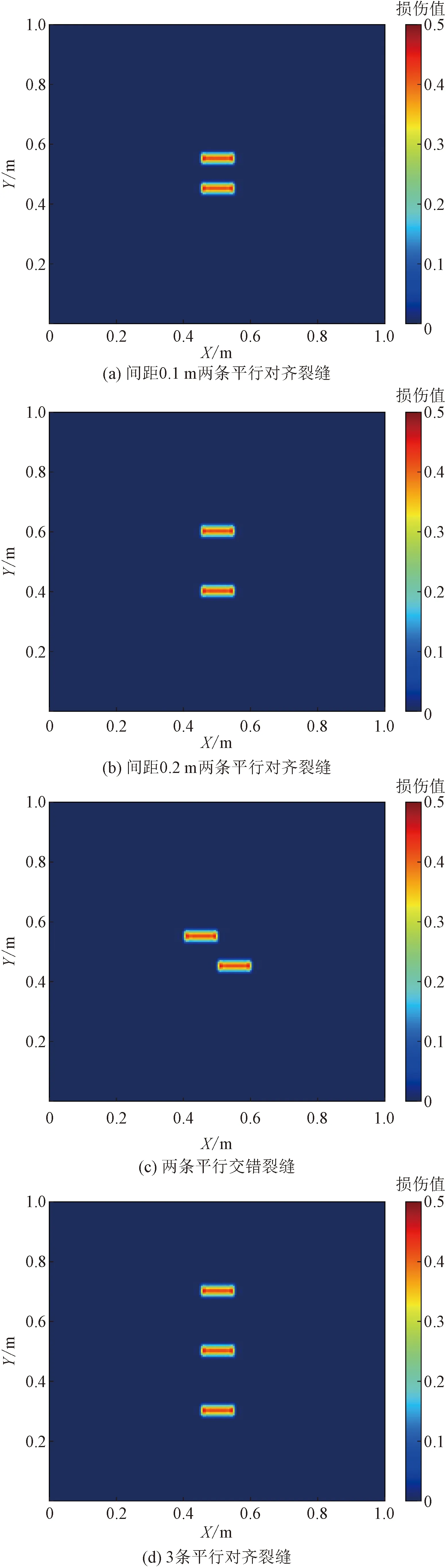
图1 模型初始损伤

3.2 结果及分析

3.2.1 间距不同的两条平行对齐裂缝

图2所示为间距0.1 m的两条裂缝扩展后的损伤、压力和垂向位移。

图2(a)表明，当两条水平对齐的裂缝同时扩展后，由于裂缝间的应力干扰，两条裂缝呈一定角度向着相反的方向偏转；图2(b)表明，水压力分布在裂缝内，作为裂缝扩展延伸的牵引力；图2(c)表明，两条裂缝内侧的物质点垂向移动受到限制，而在两条裂缝外侧的物质点垂向移动未受到限制。

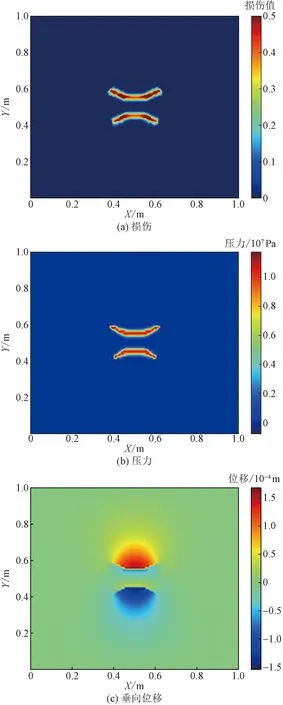
图2 间距0.1 m两条裂缝扩展结果

出现两条裂缝向相反方向偏转现象的原因如下。

(1)对于上侧裂缝，上侧裂缝物质点与下方基质物质点的间距减小，下方基质物质点作用在上侧裂缝物质点方向向上的作用力增大，导致上侧裂缝向上方偏转。

(2)同理，对于下侧裂缝，下侧裂缝物质点与上方基质物质点的间距减小，上方基质物质点作用在下侧裂缝物质点方向向下的作用力增大，导致下侧裂缝向下方偏转。

图3所示为间距0.2 m的两条裂缝扩展后的损伤、压力和垂向位移。图3(a)表明，当裂缝间距增加为0.2 m时，裂缝偏转角变小。

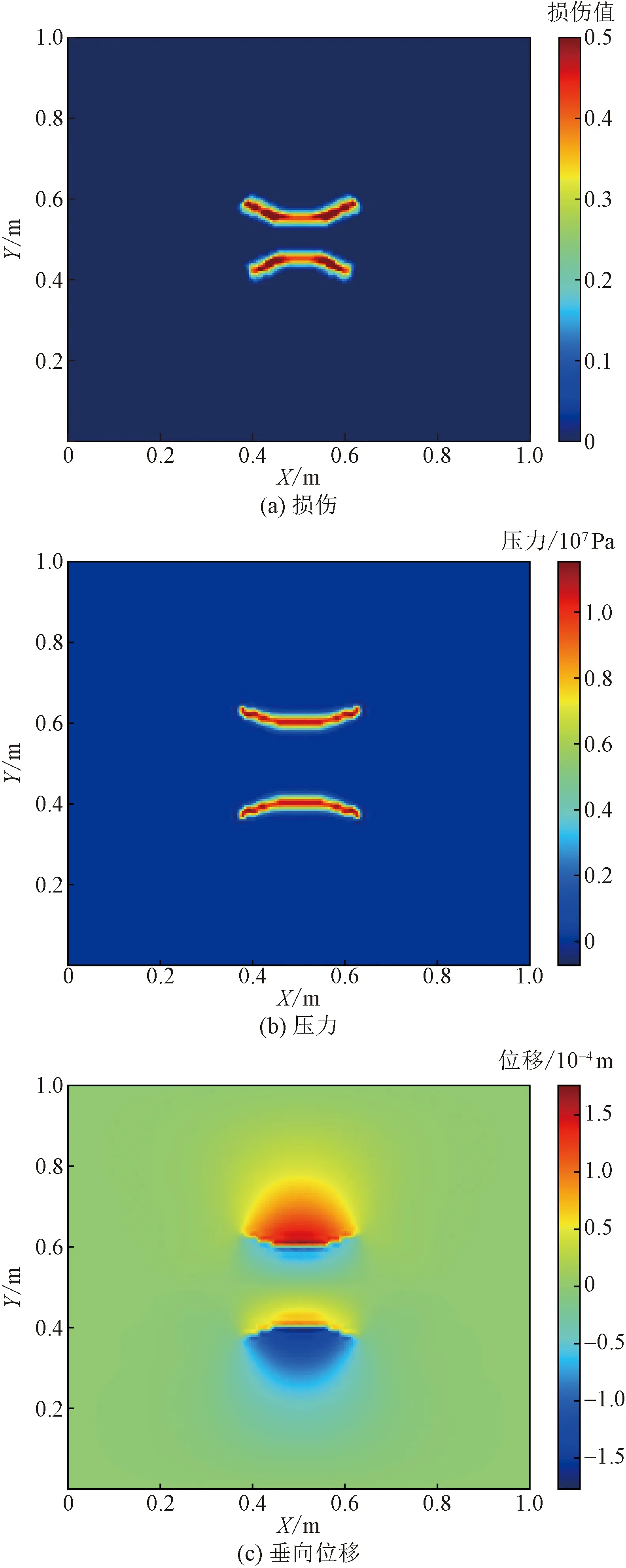
图3 间距0.2 m两条裂缝扩展结果

3.2.2 两条平行交错裂缝

图4所示为两条交错裂缝扩展后的损伤、压力和垂向位移。

图4(a)表明，当两条交错水力裂缝同时扩展时，由于裂缝间的应力干扰，两条水力裂缝会“互相吸引”，即两条裂缝彼此靠近的一端会向另一条裂缝偏转，与文献[14]中的现象吻合；图4(b)表明，水压力分布在裂缝内，作为裂缝扩展延伸的牵引力；图4(c)表明，两条裂缝两侧物质点的垂向移动会产生干扰。

两条水力裂缝“互相吸引”的原因如下。

在裂缝扩展过程中，由于物质点之间的作用力，两条裂缝内侧的物质点在水平方向上的移动会受到限制，位于中心区域的物质点由于应力干扰，会处于受力平衡状态而不发生移动，并且会与周围发生移动的物质点产生相对位移，当相对位移超过键的临界长度后，键断裂同时物质点出现损伤，当物质点与邻点的损伤值均超过临界损伤程度后，将物质点作为裂缝内的点，裂缝会近似沿着中心平衡区域的边界扩展，导致出现裂缝“互相吸引”的效果。

3.2.3 三条平行对齐裂缝

图5所示为间距0.2 m的三条裂缝扩展后的损伤、压力和垂向位移。

图5(a)表明，当3条平行对齐水力裂缝同时扩展时，由于裂缝间的应力干扰，中间裂缝扩展受到限制，两侧裂缝会向相反方向偏转；图5(b)表明，水压力分布在裂缝内，作为裂缝扩展延伸的牵引力；图5(c)表明，裂缝两两之间的物质点的垂向移动会受到限制。

上述偏转现象产生的原因如下。

(1)对于上侧裂缝，上侧裂缝物质点与下方基质物质点的间距减小，下方基质物质点作用在上侧裂缝物质点方向向上的作用力增大，导致上侧裂缝向上方偏转。

(2)对于中间裂缝，中间裂缝物质点与上方基质物质点及下方基质物质点间距均减小，上方基质物质点作用在中间裂缝物质点方向向下的作用力增大，限制中间裂缝物质点向上移动；同理，下方基质物质点作用在中间裂缝物质点方向向上的作用力增大，限制中间裂缝物质点向下移动，导致中间裂缝向两侧扩展均受到限制。

(3)对于下侧裂缝，下侧裂缝物质点与上方基质物质点的间距减小，上方基质物质点作用在下侧裂缝物质点方向向下的作用力增大，导致下侧裂缝向下方偏转。

4 结论

采用基于近场动力学和有限差分法结合的方法，尝试从非局部理论的角度对水力压裂中多裂缝缝间干扰问题进行模拟研究，结果表明，由于水力裂缝间的应力干扰，得出结论主要如下。

(1)同时扩展的两条平行对齐裂缝向相反的方向偏转，并且随着裂缝间距减小，偏转角度增大。

(2)同时扩展的两条平行交错裂缝会“互相吸引”，即两条裂缝彼此靠近的一端会向另一条裂缝偏转。

(3)同时扩展的3条平行对齐裂缝，两侧裂缝会向相反方向偏转，中间裂缝的扩展会受到限制。

根据研究结果，在实际的压裂设计时，根据需要考虑适度增大裂缝间距，减少裂缝间的干扰，以形成复杂的缝网结构，增大改造体积，提高最终采收率。