基于主成分分析法优化广义回归神经网络的地震震级预测

王晨晖， 袁颖， 刘立申， 陈凯南， 吴鹤帅

(1. 河北红山巨厚沉积与地震灾害国家野外科学观测研究站， 邢台 054000； 2. 河北省地震局邢台地震监测中心站， 邢台 054000； 3. 河北地质大学城市地质与工程学院， 石家庄 050031； 4. 河北省地下人工环境智慧开发与管控技术创新中心， 石家庄 050031)

中国地震灾害频发，灾难性地震常常造成巨大的人员伤亡和财产损失，因此科学有效地进行地震预测对于防震减灾具有重要的指导意义[1-2]。

由于震级与其影响因子存在错综复杂的联系，普通的数学公式很难表达这种复杂的非线性关系，为此，许多专家学者进行了长期的探索。邓世广等[3]采用贝叶斯定理和综合概率法得到了年度地震危险概率预测结果。曹凤娟等[4]采用层次分析法建立了辽宁地区中强震预测指标体系进而计算各指标的权重。孙颖等[5]利用层次分析法求出桥梁震害各影响因子的重要度。以上传统研究方法均取得了良好的效果，但预测结果依赖专家经验，容易受主观因素影响。面对上述问题，神经网络等人工智能算法应运而生，并在地震震级预测领域得到了广泛的应用。徐程等[6]以滇西南地震数据为学习样本建立了反向传播(back propagation，BP)神经网络模型。蔡润等[7]将BP网络和SOM网络联合引入到地震震级的预测中。董晓娜等[8]采用《中国震例》作为数据源，通过初步整理分析和预处理，构建了较完备的震例研究样本集。但由于地震震级影响因子众多，单一地选用哪种评价方法，都会面临处理大量数据的问题，同时各影响因子与地震震级之间复杂的非线性关系导致模型学习效果不佳，预测精度较差。而BP神经网络易陷入局部最优，还需探索更为有效的科学方法。

广义回归神经网络(general regression neural network，GRNN)是经典的前馈式局部逼近神经网络，具有计算速度快、全局最优性等特点。粒子群优化算法(particle swarm optimization，PSO)是一种全新的参数寻优方法，它不仅可以辅助GRNN模型寻优，还可以调整模型结构，以此提高构建模型稳定性。基于此，现利用主成分分析法对7个影响因子进行降维处理，以新生成的4个主成分作为模型输入变量，地震震级为输出变量，运用粒子群算法寻优得到模型最优光滑因子，最终建立基于PCA-PSO-GRNN的地震震级预测模型，将建立的PCA-PSO-GRNN模型应用于光滑因子测试样本，实现地震震级预测。

1 基本原理

1.1 主成分分析法

主成分分析法是将原始变量重新线性组合成新的互不相关的新变量，即主成分，新生成的主成分维度降低且保留原始变量的绝大部分信息[9-12]。具体过程为：设(X1,X2，…，Xn)是总体X的n个样本，每个样本包括m维变量，该矩阵可表示为

(1)

首先计算矩阵的协方差阵，求出其对应的相关系数阵。然后求出相关系数阵的特征值，且满足λ1≥λ2≥…≥λm≥0，则第i个主成分的贡献率为

(2)

前q个主成分的累计贡献率为

(3)

当前q个主成分累计贡献率达85%以上时，用这q个主成分来代替初始的影响因子进行分析一般是满足要求的。

1.2 粒子群算法

PSO算法首先初始化n个粒子，每个粒子代表GRNN一个光滑因子，粒子通过不断迭代寻求自身最优解Pbest，然后比较每个粒子的Pbest，寻优得到整体最优值Gbest，即粒子通过不断搜寻Pbest和Gbest并通过计算得到最新速度V和位置Y(设有D维空间)，全部完成迭代，得到Gbest最优值[13-16]，即

(4)

(5)

式中：d=1,2,…,D;i=1,2,…,n;k为当前迭代次数；ω为惯性权重；Vid为粒子的速度；Yid为粒子的位置；c1、c2为加速度因子；r1、r2为[0,1]区间的随机数；Pid、Pgd分别为第i个粒子的个体极值位置和群体极值位置。

1.3 广义回归神经网络

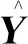
(6)

假设f(x,y)服从正态分布，则有

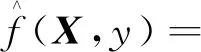
(7)

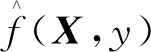
(8)

GRNN的网络结构由以下4个步骤实现。

步骤1输入层。该层神经元个数对应输入变量xi即主成分个数。将PCA降维得到的3个主成分作为GRNN模型输入变量，因此输入层神经元个数为3。

步骤2模式层，该层神经元个数等于训练样本的数量。每个神经元传递函数为

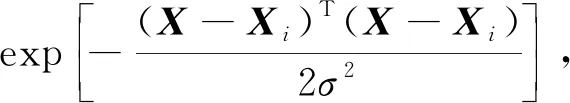
(9)

步骤3求和层。该层由2种求和方式，一种是算数求和SD，另一种是加权求和SNj，传递函数分别为

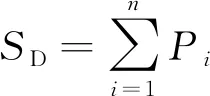
(10)

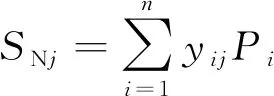
(11)

式中：Pi为模式层第i个神经元的传递函数；yij为模式层第i个神经元与求和层第j个分子求和神经元连接权值。

步骤4输出层。该层神经元个数只有1个，即地震震级。将SNj与SD相除，得输出结果，即

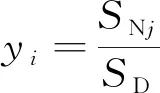
(12)

2 模型建立与预测

基于PCA-PSO-GRNN的地震震级预测模型构建流程图如图1所示，具体步骤如下。

Step 2.Construct the matrixand root the polynomial to obtain the frequency parameter estimatesNote that the roots are inside the unit circle and are closest to the unit circle.

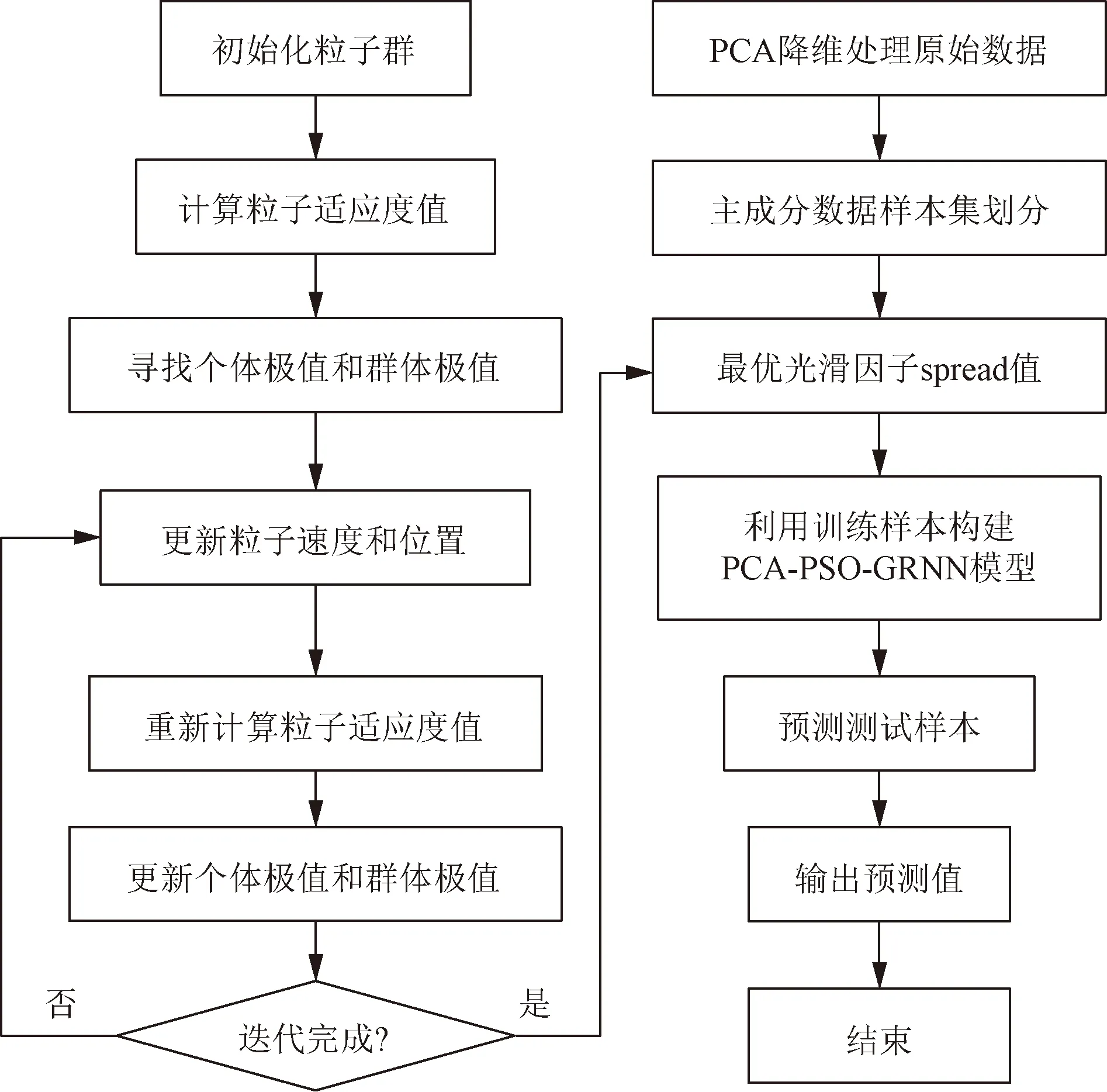
图1 PCA-PSO-GRNN模型流程图

步骤1按式(13)对7个影响因子数据进行归一化处理。

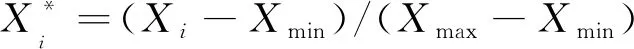
(13)

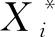
步骤2对利用进行降维处理，形成新的主成分，以新生成的主成分作为输入变量。

步骤3利用PSO算法寻求GRNN最优光滑因子，构建基于广义回归神经网络的粒子群算法优化的地震震级预测模型。

步骤4将建立的PCA-PSO-GRNN模型应用于地震震级测试样本，实现地震震级预测。

2.1 数据来源

通过查阅文献，并结合前人经验选取文献[6]的地震数据作为研究样本，地震样本部分原始数据如表1所示，其中b值为震级和频度关系式中的比例系数。

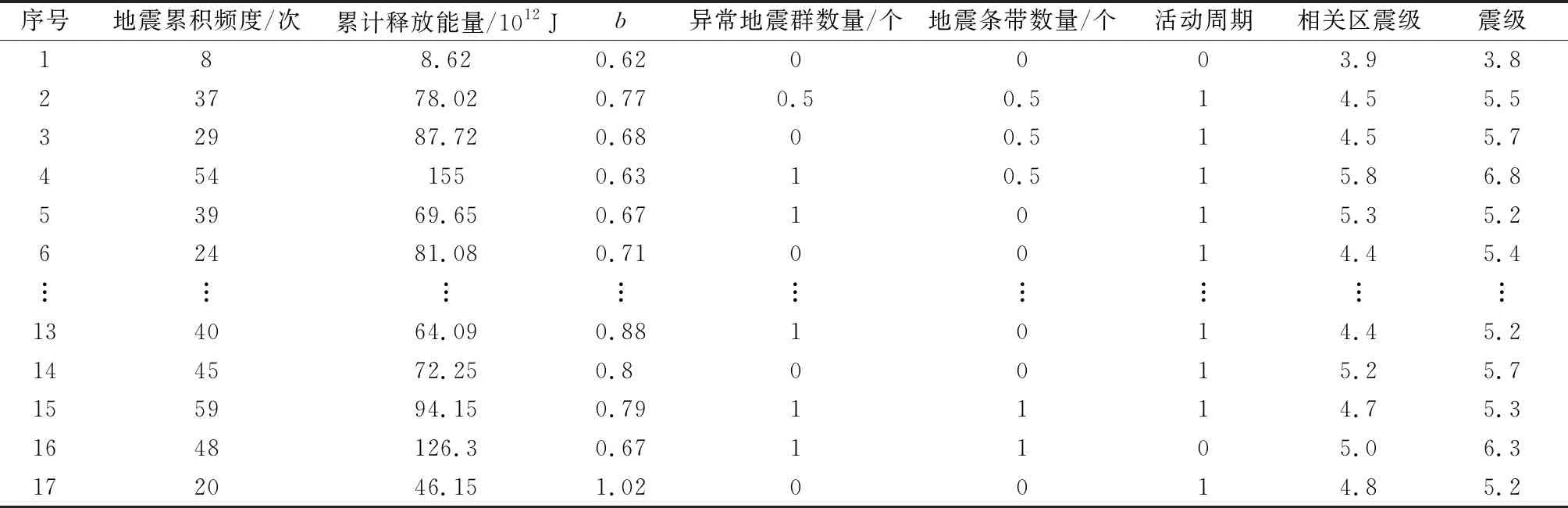
表1 地震样本部分原始数据

2.2 主成分分析

利用PCA对7个地震震级影响因子进行分析，得到归一化特征值，各成分贡献率和累计贡献率如表2所示。从表2可以看出，前3个主成分的累计贡献率为88.348%，基本能够反映原来7个变量所携带的信息。由成分得分系数矩阵可以得到4个主成分的表达式见式(14)。将提取出的4个线性无关的主成分代替原来的7个影响因子作为输入变量来建立GRNN模型，有效降低了变量的维数，提高了模型的运算效率。

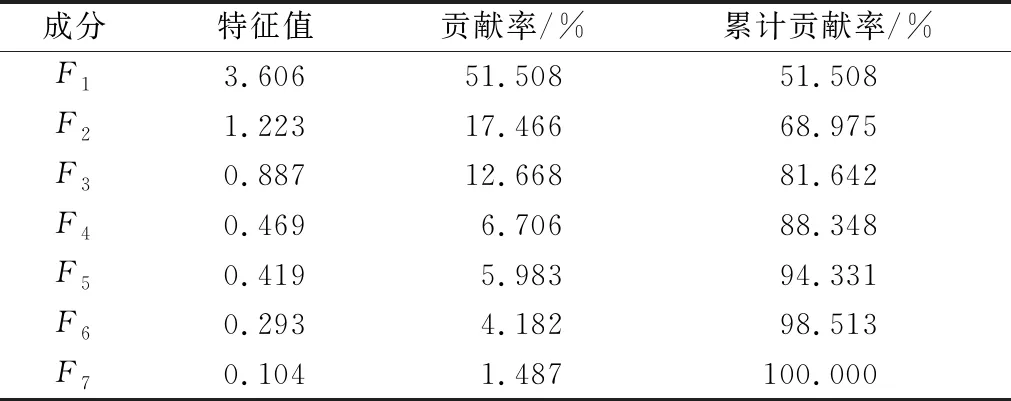
表2 主成分特征值、贡献率和累计贡献率

(14)

式(14)中：x1为地震累积频度；x2为累计释放能量；x3为b值；x4为异常地震群数量；x5为地震条带数量；x6为活动周期；x7为相关区震级。

根据前4个主成分的表达式，从而得到新生成的主成分数据样本，随机选出10个训练样本和7个预测样本。

2.3 预测结果分析

以新建立的4个主成分数据为整体样本，随机选取10组训练样本训练PCA-PSO-GRNN模型，并利用建好的模型对剩余7组测试样本进行测试，运用均方根误差(RMSE)、决定系数(R2)、均方相对误差(MSRE)和平均绝对误差(MAE)对模型训练样本回判结果和测试样本预测结果进行误差分析，计算公式如下。

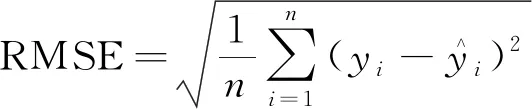
(15)

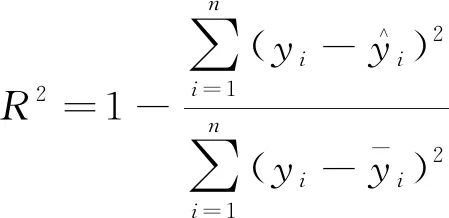
(16)

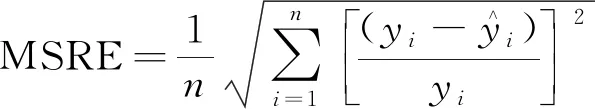
(17)

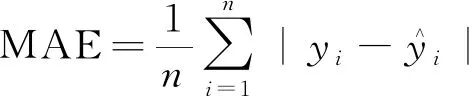
(18)

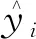
基于PCA-PSO-GRNN模型的地震震级训练样本和测试样本的误差分析结果如表3所示，训练样本回判结果和测试样本的预测结果如图2和图3所示。由表3和图2、图3可知，训练样本回判值与实际值基本一致，回判效果较好，平均误差率为5.84%，测试样本的预测值与实际值的平均误差率为5.17%，满足实际要求。PCA-PSO-GRNN模型训练样本和测试样本的误差分析如表4所示，由表4可以发现训练样本和测试样本的RMSE分别为0.114 0和0.100 0，表明模型训练精度较好。训练样本和测试样本的R2分别为0.983 4和0.986 8，表明模型的拟合程度较高。此外，测试样本的MSRE和MAE分别为0.007 3和0.100 0，均低于训练样本，表明模型预测精度表现良好。

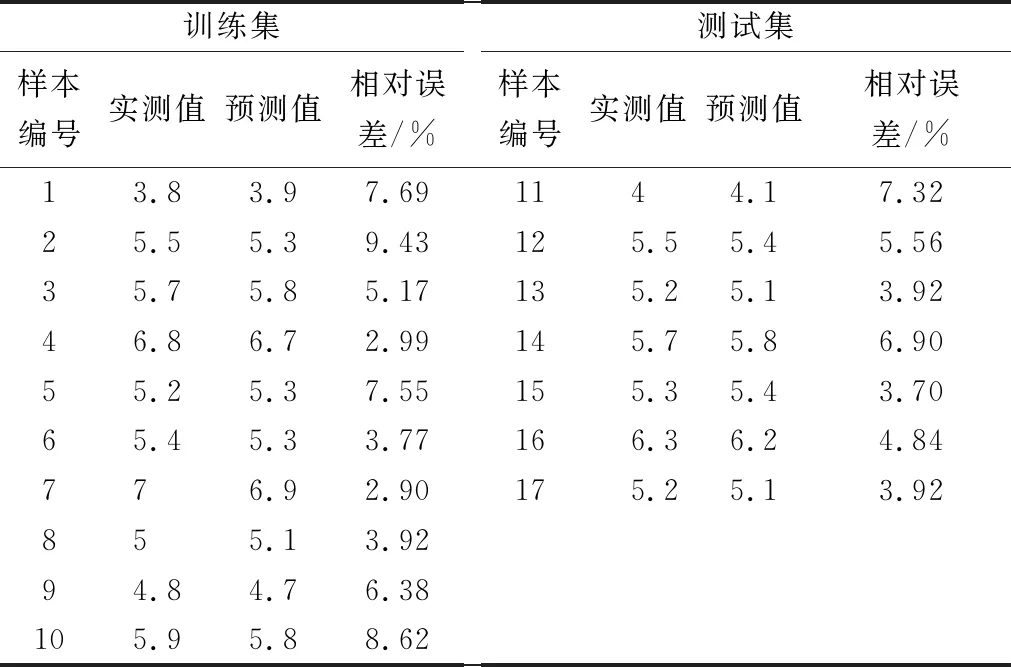
表3 PCA-PSO-GRNN模型误差分析表

表4 训练样本与测试样本误差分析

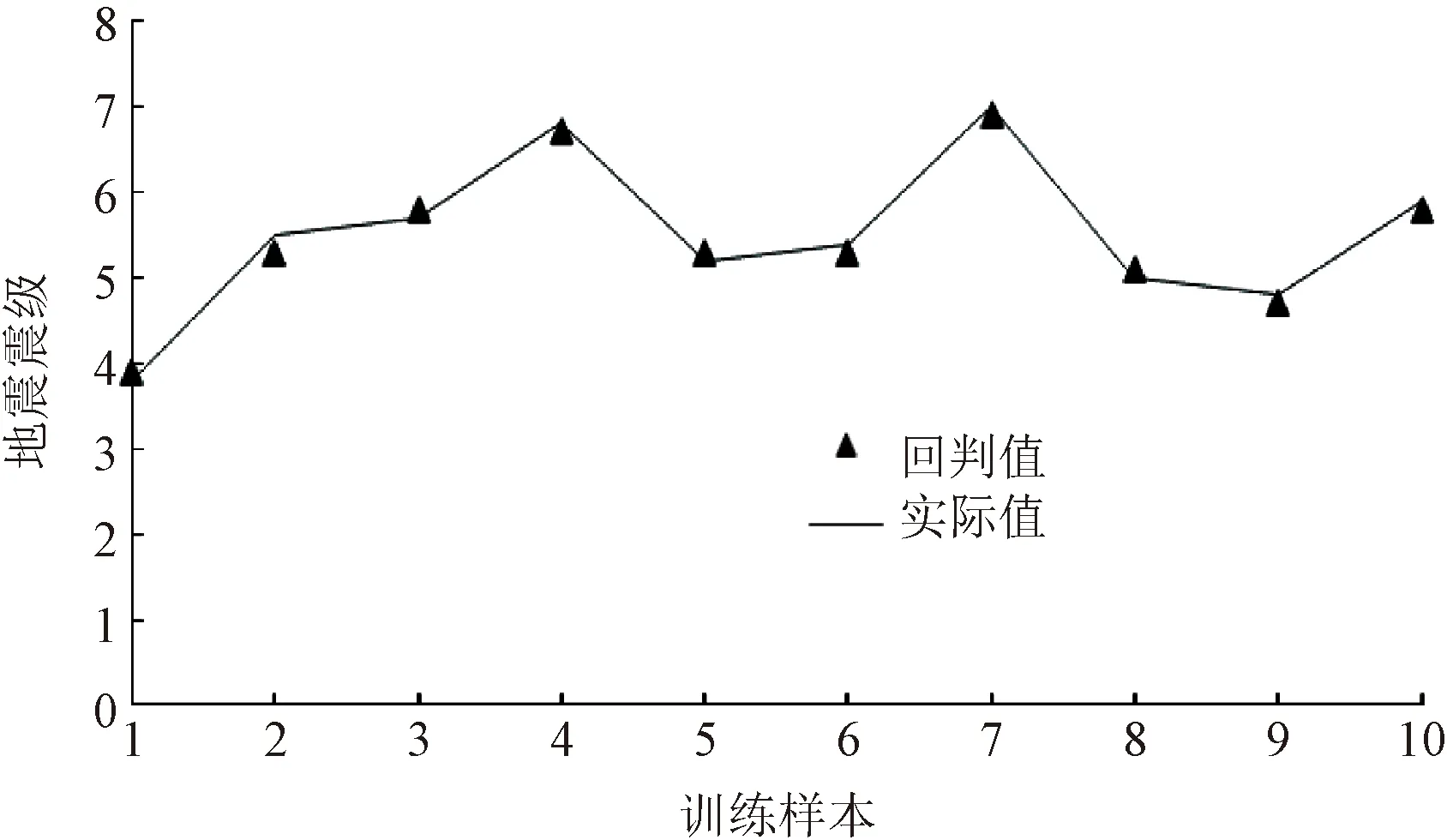
图2 训练样本回判值与实际值对比

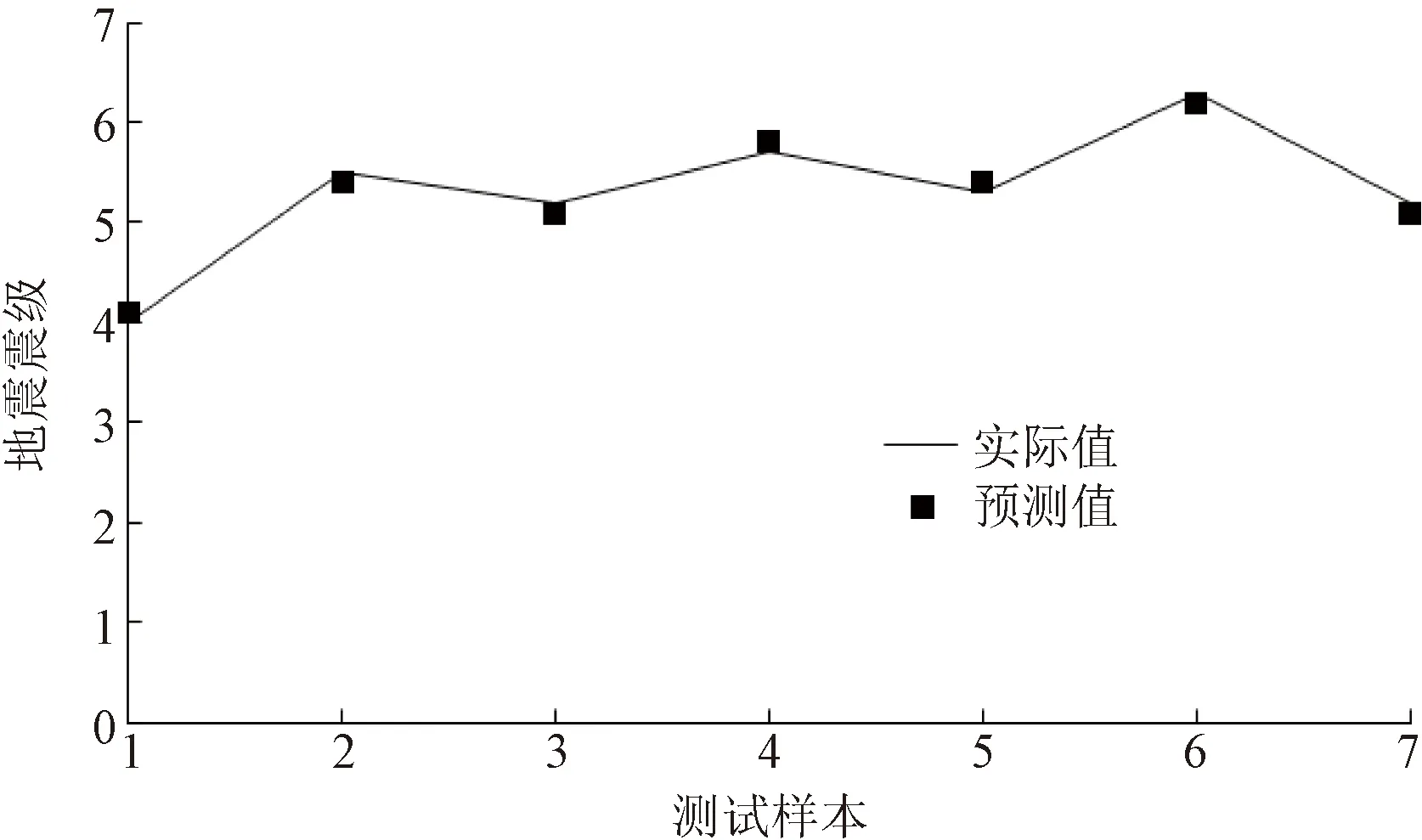
图3 测试样本预测值与实际值对比

为了更好地评判模型的有效性和泛化性能，将PCA提取的4个主成分作为各模型的输入变量分别建立BP模型和未经PSO优化的GRNN模型，并对测试样本分别进行预测，BP神经网络、单一GRNN网络与PCA-PSO-GRNN模型的模拟结果进行对比，预测结果误差分析如表5所示。可见，PCA-PSO-GRNN模型的预测效果显著优于其他2种模型，决定系数R2分别较BP模型和标准GRNN模型提高8.93%和21.56%，因此，采用PCA降维处理且利用PSO优化的GRNN模型具有更好的泛化性能和预测能力。

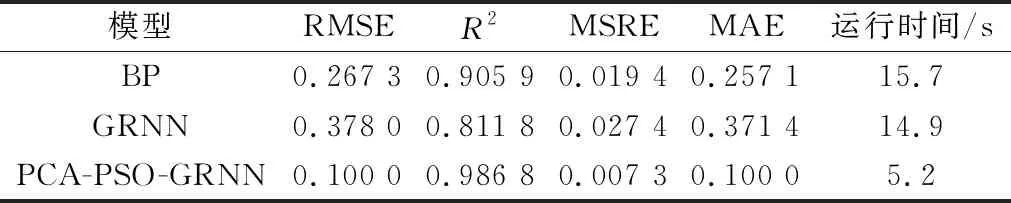
表5 3种模型误差分析

3 结论与分析

(1)采用PCA对影响地震震级的7个影响因子进行降维处理，模型输入维度由7维降至4维，优化了模型结构，提高了模型运行效率。

(2)利用PSO寻优得到最优光滑因子，通过对模型的回判结果和预测结果进行误差分析，得到训练样本的RMSE、R2、MSRE和MAE分别为0.114 0、0.983 4、0.006 8和0.110 0，测试样本的RMSE、R2、MSRE和MAE分别为0.100 0、0.986 8、0.007 3和0.100 0。

(3)PCA-PSO-GRNN预测精度和运行效率均优于BP模型和单一GRNN模型，可以为地震震级预测提供参考。