顶张力立管三维涡激振动研究❋

崔 鹏，郭海燕，顾洪禄，李效民，李福恒

(中国海洋大学工程学院，山东 青岛 266100)

当海流流经立管时，在一定条件下会发生漩涡脱落的物理现象，漩涡脱落会对立管产生周期性的可变力，导致立管发生垂直于来流方向的多模态振动，该现象称为涡激振动。涡激振动是立管疲劳破坏的主要因素之一，当漩涡脱落频率与立管结构自振频率接近时，漩涡的泄放过程将被结构的振动频率所控制，发生频率“锁定”现象，此时立管振动强烈，振幅增大，加剧疲劳。立管一旦出现安全问题，将会造成巨大的经济损失和严重的海洋污染和次生灾害，因此必须加深对立管涡激振动动力特性的研究，确保其在服役期间的具有足够的安全性和可靠性。

针对立管涡激振动的数值模拟，国内外许多学者进行了大量研究。Park等[1]采用有限元方法研究了细长立管的涡激振动动力响应，研究中考虑了浮体运动对立管动力响应的影响，并进行了波流激励分析和参数激励分析。Holmes等[2]对网格划分技术进行改进，并提出了一种能够在网格划分稀疏的条件下分析立管的方法，该方法能够模拟任何攻角的位置、斜立立管和其他的几何形状，它将三维计算流体力学和顶张力立管结构模型相结合来预测涡激振动，克服了二维分析方法的部分缺点。Huang等[3]使用张拉梁模型建立了顶张力立管控制方程，采用了隐式的中央差分法对立管的运动控制方程进行离散，结合有限元方法对长细比在482～3 350范围内的3根立管进行了数值模拟，得到的结果与已发表的试验数据和商用软件吻合良好，该方法在空间上具有二阶精度，在时间上具有一阶精度。

国内,徐万海等[4]在研究影响张力腿因素的研究中，基于Euler-Bernouli梁模型分别建立了线性模型和非线性模型，采用有限差分法对方程进行求解，分析了两种模型在预测结构动力响应方面的差异性，非线性模型的计算结果相比线性模型偏小，当平台运动幅值增大时，2种模型计算结果差异明显。唐国强等[5]采用梁结构模型建立一种经验模型，对柔性立管涡激振动进行了分析。唐友刚等[6]考虑张紧器张力变化，结合尾流振子模型，建立了剪切流场的顶张力立管模型，对影响立管涡激振动特性的各种因素进行了参激分析。万德成等[7]基于自主开发的CFD求解器，采用切片模型，对恒定张力和变张力的柔性圆柱的涡激振动进行了仿真模拟，结果表明变张力条件会显著增加圆柱体在振动过程中的位移响应。当轴向张力以一阶固有频率变化时，位移增幅约为一倍，当轴向张力以二阶固有频率变化时，位移增幅约为25%。李效民等[8]采用向量式有限元方法建立管动力学模型，编写了立管动力分析程序，对顶张力立管的动力响应特性进行了分析，通过与Euler-Bernouli梁模型的数值模拟结果进行对比，证明向量式有限元方法可以应用于立管的动力行为分析。典型的Euler-Bernouli梁模型通常忽略剪切变形，同时不考虑到轴向位移和轴向力的变化，对于处于垂直状态的顶张力立管，轴向张力扮演着重要角色，其对立管动力特性的影响不可忽略。

目前关于顶张力立管的研究大部分假设立管两端铰接，没有考虑顶端运动和顶端张力变化的影响。本文考虑轴向变形，采用弹簧模型模拟立管张紧器对立管作用，基于一种新的有限元方法——向量式有限元方法，以物理模式建立了立管三维非线性振动模型，该模型将立管离散为有限数目的满足牛顿第二定律的质点，以质点为控制对象建立立管控制方程，计算流程是逐点并逐步循环的，不需要集成刚度矩阵，避免了矩阵不收敛或出现病态的情况，通过显示中央差分法求解质点位移得到结构单元变形，通过材料力学理论求解单元内力，没有作位置变化和变形的分离，对于求解大变形大变位的立管模型，该方法简单可靠同时求解方便。

1 基于向量式有限元的立管模型

1.1 立管模型控制方程

如图1所示，假定该顶张力立管长度为L，在顶部张力与重力的共同作用下处于垂直位形，作用在立管顶部的张力由刚度为Ks的弹簧来施加。弹簧用来替代真实情况下张紧器的功能，整体坐标系的原点设置在立管的底部，X轴的方向与海流来流方向平行；Z轴与初始时刻的立管轴线相重合，正方向指向水面；Y轴与另外两个轴的方向相互垂直。假设立管初始长度为L，将立管均分成N段，形成N+1个质点(从下向上依次编号为1，2，3，…，i，j，…，N，N+1)，假设任意点的坐标为Xi=(xi,yi,zi)T，根据向量式有限元的点值描述，则立管的初始状态可以定义如下：

(1)

式中：i=1,2,3，…，N+1。

质点的控制方程如下:

(2)

(3)

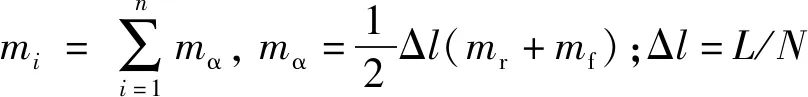
本文模型中，初始时刻只考虑作用在立管上的预加顶部张力、重力和浮力，后期水动力的计算采用向量式有限元斜坡加载函数进行加载。张力通过弹簧直接作用到立管顶部的质点上，某一时刻的张力可以表达为：

T=T0+KsΔtop。

(4)

式中：T0为初始时刻的预加顶部张力；Ks为顶部弹簧刚度系数；Δtop为立管模型顶部质点的竖向位移。在初始时刻，Δtop=0，T=T0。

本文立管模型中用有限数量的质点作为控制变量，通过质点的位置变化和运动轨迹描述立管结构的运动状态，根据结构为物理连续，结构相邻质点之间点的位置使用标准内插函数计算，结构行为和性质对空间的变化是点值的差，对时间的变化是一组常微分方程，从而回避了立管结构控制上使用偏微分方程。利用质点描述立管结构的空间位置和立管结构运动轨迹，在描述结构力学状态方面较为方便，尤其在处理立管这种具有大几何变化的三维空间柔性结构时，立管结构的描述不需要使用微分方程控制，因不需要结构分析中的许多简化，该模型优势更为明显。

1.2 途径单元

当杆件受到外力作用时，将立管结构上空间点的位置向量看作是一个有关时间的函数，称之为途径或时间轨迹。如图2所示，假设计算开始及结束时间分别为t0和tn，将整个计算时间t0～tn离散为一组时间点t0，t1，t2，……,tn，其中任一时段ta～tb被定义为一个途径单元。在途径单元ta≤t≤tb内，空间点ta、t、tb的位置向量分别为xa、x、xb，途径单元解决的问题就是空间点从xa转换到xb的问题，在转换过程中，空间点满足变形和运动力学准则，轨迹则是时间的连续函数。结构运动满足的力学定律为运动定律和胡克定律，即空间点位移遵循运动公式，杆件元变形遵循应力和应变的关系公式，对于大变形问题，经过简化后可以用大变位小变理论来解决。

1.3 逆向运动

向量式有限元通过逆向运动解决空间杆件元的变形问题，如图3所示，将杆件元从A到B位置先经逆向平移，再经过逆向转动至途径单元初始时刻ta位置，杆件元虚拟形态与ta时形态之间的差异是一个小变形和小刚体运动行为，以ta时形态作为计算变形参考，根据微应变和工程应力空间计算杆件元的小变形和小刚体运动。得到杆件元纯变形之后，进而可以计算杆件元节点内力。

1.4 节点内力计算

根据材料力学相关理论及计算得到节点的变形和转角，对于轴力计算采用胡克定律，弯矩计算采用非对称截面的挠曲理论，扭矩和剪力计算采用剪切胡克定律，则节点内力和弯矩计算如下：

(5)

每一个杆件元共有12个力，由于杆件元的质量都集中到质点，杆件元没有质量，必须满足结构的静力平衡条件，根据力平衡方程，即可得到其它6个力分量。

1.5 流体力计算

立管服役期间的环境载荷包含众多载荷，考虑到本文重点研究立管涡激振动的动力响应以及内流对立管涡激振动的影响，在本文中主要考虑海流载荷。

考虑海流的流速和流向比较稳定而且海流的速度场剖面随水深的变化是缓慢的，在计算中近似的认定海流载荷为定常载荷。如图4所示，水平拖曳力FD与水质点的运动方向有关，由于涡激振动会引起圆柱体的水平振动，此时，海流方向U与圆柱体结构运动方向V产生相对速度UR=U-V，涡激振动引起的升力垂直于相对速度方向，顺流向的水平拖曳力FD和横向FL的升力表达式为：

(6)

(7)

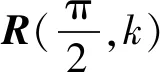
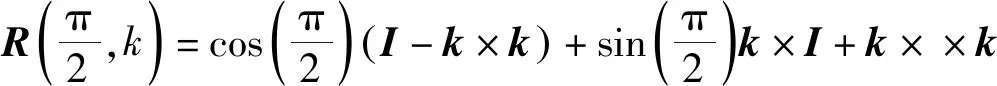
(8)

式中：I=i×i+j×j+k×k为单位张量，i,j,k分别为沿X，Y，Z轴的单位方向矢量。

顺流向曳力系数和横向升力系数表达式为

(9)

(10)

式中：CD0为平均曳力系数；CflD为弹性支撑运动圆柱体波动曳力系数；CflD0为固定静止圆柱体波动曳力系数；CL0为固定静止圆柱体波动升力系数；ω和q分别为圆柱体顺流向和横向的无量纲尾流振子系数。

相对速度表达式为：

(11)

(12)

对于相对速度绝对值|UR|，采用泰勒公式，并忽略高阶项的方式得到

(13)

可得曳力在X轴方向和Y轴方向分力分别为

(14)

(15)

同理可得升力在X轴和Y轴分力，则立管在X轴是流体力为升力和拖曳力在该方向上的分力之和，同理可得Y轴上的流体力。

1.6 尾流振子模型

本文涡激振动模型采用Modified-Rayleigh尾流振子模型，该尾流振子方程为

(16)

(17)

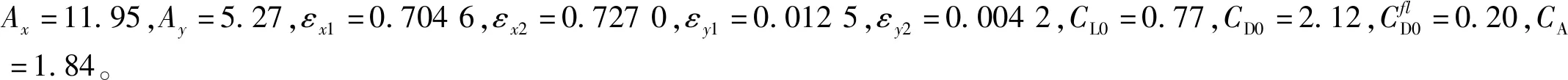
1.7 立管模型数值求解

本文采用中央差分法求解运动公式，作为一种常用的显式积分法，避免了隐式积分法的迭代问题和复杂的收敛问题，在求解结构的瞬时高度非线性问题时，显式积分法的优越性更加明显。中央差分公式为

(18)

(19)

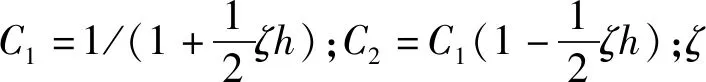
2 立管涡激振动分析

为验证本文涡激振动模型的准确性，采用Chaplin[9]中的试验作为参考，该试验布置简图如图5所示。立管参数为管长13.12 m，管径0.028 m，长细比为467，质量线密度为1.85 kg/m，质量比为3.0，结构阻尼因子为0.33%，抗弯刚度为29.9 N·m。该试验通过大气压原理巧妙地设计了一个试验装置，在6.5 m的水槽中成功的进行了13.12 m长的立管涡激振动实验，顶端55%长度处于静水中，其余立管被置于运动水流中，流速最高为1 m/s，雷诺数范围为2 800～28 000,顶部弹簧刚度系数为38.5 kN/m,立管两端铰接，顶端施加预张力。

通过选取Chaplin等[10]中流速为0.31和0.95 m/s两种工况进行对比，验证本文模型的有效性。其对应的顶部张力分别为457和1 002 N，数值模拟中，设置单元数为400，时间步长为h=2×10-5。

如图6(a)、7(a)所示，最大顺流向无量纲位移为5.189和10.260，其对应的试验结果为3.960和11.350，因此计算结果同试验结果较相近。Chaplin的预报结果中仅有2种经验模型给出了顺流向的位移预报，而且预报结果比试验结果小很多，相比之下本文模型预报结果在准确率方面达到80%以上，在可接受范围内。

图6(c)、(e)和图7(c)、(e)皆为立管顺流向和横向的位移时程图，立管的横向振动表现为驻波现象，但是顺流向发现行波的存在，此时，行波从结构振动幅度较大的区域向振动幅度较小的区域传播，也就是从能量输入区向能量输出区传播，这也符合模型中立管上方水流静止，下方为运动水流的情况。随着流速的增加，行波现象更加明显(见图6(b)和图7(b))，但是这一现象在试验中并未发现，这可能是试验中的立管具有较小长细比而预加张力较大、干扰因素较多。

0.95 m/s工况的流速虽然要远大于0.31 m/s，但是由于对应的顶部预加张力远大于0.31 m/s工况的流速对应的顶部预加张力，且其顺流向位移均方根反而远小于0.31 m/s时的顺流向位移均方根。这说明相对流速，顶部张力对顺流向的振幅作用更加明显，可以通过增加顶部张力的方式来减弱横向涡激振动。图6(b)和图7(b)显示顺流向位移的均方根要比横向位移均方根要小很多，只有横向位移的15%～20%左右，这也是之前的大部分涡激振动研究都关注横向振动的原因，但是考虑到立管涡激振动的顺流向振动频率接近横向振动频率的两倍，对于立管涡激振动的分析，尤其是涡激振动疲劳分析，需要重视立管顺流向涡激振动可能造成的疲劳破坏。

通过与试验对比可知，本文建立的模型同时考虑立管的顺流向和横向涡激振动，在预报立管涡激振动的位移、模态等方面的准确程度是较高的，因此，对立管的涡激振动预报是有效的。

本文模型采用的时域分析发现了行波现象，由于行波效应的存在，立管涡激振动的动力响应和导致的疲劳规律同驻波效应有着明显的区别，尤其对于分析行波效应起主导作用的大长细比立管时，采用频域分析方法预报立管的疲劳具有一定的局限性，因此在复杂海洋环境中需要长时间安全服役的立管，在分析其涡激振动导致的疲劳时，采用时域分析方法更加合理。

3 立管轴向变形和轴向张力分析

向量式有限元采用空间弯曲杆件元来模拟立管各个质点间的相互作用。质点是广义质点，对于空间问题，质点具有6个位移分量即3个平移分量和3个转动分量，点之间的内力有轴力、扭矩和两组弯矩及剪力，并不像大多数研究者那样忽略剪切和扭转变形甚至轴向变形的影响，本文基于向量式有限元建立的模型是一种真正的三维模型，能够更加真实模拟立管的行为。

从图8、9可以看出立管轴向位移和轴向张力是周期性振动的，而且频率相同，其频率与立管顺流向振动频率接近，这说明立管的轴向变形主要是由顺流向振动引起的，这主要是因为顺流向的平均曳力要远大于涡激振动升力和波动曳力，从而导致立管顺流向位移远大于横向位移。尽管立管的轴向位移变化相对立管整体长度很小，但是根据胡克定律，当立管材料的劲度系数很大，较小的轴向位移也会引起较大的轴向力的变化。立管初始顶端张力为1 002 N，9.84 m处的初始张力为958 N，从图9中可以看出，立管涡激振动达到稳定状态时，9.84 m处的轴向张变化范围为987.5～1 197 N，比轴向力初始值高出3.08%～24.95%，因此轴向变形引起的轴向张力的增大是不可以忽略的。

从图10可以看出立管轴向变形最大处接近于立管顺流向位移最大处，说明轴向变形主要是由于顺流向位移引起。从图11可以看出立管轴向张力从立管顶部到底部是逐渐较小的，立管顶部的张力变化范围最大，其最大张力超出预加顶部张力27.3%，立管底部的张力的变化范围最小，但是其张力仍大于其初始张力值，因为顶部张力对于顶张力立管的动力响应有重要影响，因此不能忽略轴向变形引起的轴向张力的变化。本文立管模型的一大优点是考虑立管轴向变形和轴向张力变化，是一种真正的三维模型。

4 结语

本文采用向量式有限元方法，使用弹簧模型模拟立管张紧器对立管作用，将立管离散为有限数目的满足牛顿第二定律的质点，以质点为控制对象，给出立管控制方程，建立了立管三维非线性振动模型，考虑立管和流体之间相对速度，采用Modified-Rayleigh尾流振子模型，推导了作用在立管上的流体力计算公式，并采用显示中央差分法对立管模型进行数值求解。

通过对立管顺流向、横向和垂向三维耦合涡激振动动力响应进行计算，并将计算结果同试验结果对比可知，本文模型能较准确地预报立管的涡激振动动力响应。通过对立管轴向变形以及轴向张力变化的分析，发现立管轴向变形会引起立管轴向张力的明显增大，影响立管涡激振动的动力响应，在立管的分析中，轴向变形引起的轴向张力的变化是不可忽略的。