波浪非线性对溶质进入海底沉积物运移过程影响研究❋

刘小丽，贺建檩

(1.山东省海洋环境地质工程重点实验室，山东 青岛 266100；2.中国海洋大学 环境科学与工程学院，山东 青岛 266100)

大量污染物的排海以及海上溢油事件的频发，使得海洋环境污染问题受到越来越多的关注。悬浮于水体中的污染物质，在水动力的作用下会进入到海底的沉积物中，从而对海洋生态环境产生进一步影响。波浪作用下污染物质(溶质)进入沉积物迁移过程的研究，对于海洋环境的评估具有重要意义。

作为近岸海域中压力梯度的来源，波浪会引起海底沉积物中孔隙水的渗流，其对溶质输运的影响不容忽视[1]。对于平底海床，由于规则波的周期循环特征，一个波浪周期内上覆海水与沉积物床之间的净交换水量基本为0，因此，当海水与沉积物界面上的溶质浓度均匀分布时，规则波作用下对流作用对溶质在沉积物中的运移过程的贡献可以忽略[2-4]。Harrison等[2]对波浪作用下溶质进入平海床运移特征的理论分析表明，波浪通过促进溶质的机械弥散作用而加速溶质的迁移，波浪作用下溶质在沉积物中的有效扩散率可比分子扩散速率大4个数量级。Clark等[5]通过波浪水槽试验研究了行进波对溶质进入砾石床运移特征的影响，结果显示，行进波极大程度地提高了溶质进入底床的运移速率和运移深度，而进一步的理论分析表明，行进波主要通过增强机械弥散作用促进溶质运移。波浪作用下上覆水体与沉积物床之间的溶质交换过程可以通过溶质的对流-弥散方程进行描述。Qian等[6]基于二维溶质对流-弥散方程，对线性行进波和驻波作用下溶质进入湖床沉积物的溶质扩散过程进行了数值模拟，计算结果表明，波浪作用可以使湖床沉积物对氧的吸收率提高2个数量级。Geng和Boufadel[7]利用溶质对流-弥散方程，通过数值模拟研究了波浪和潮汐作用下浅滩含水层溶质运移特征，结果表明，海洋水动力改变了溶质运移的路径，波浪增加了滩面的交换通量，并拓宽了溶质交换区域。刘小丽和刘明珠[8]基于二维Biot固结理论和对流-弥散方程，考虑了波致海底沉积物的变形效应，对行进波作用下海水中的溶质进入沉积物中的运移过程进行了数值模拟，计算结果表明，沉积物的变形效应会促进溶质的运移速率，增大溶质的运移深度。

以上研究表明，波浪对溶质进入沉积物的运移过程具有明显的促进作用，利用溶质的对流-弥散方程可以较好地模拟水动力作用下溶质的运移过程，但目前绝大多数的研究都是基于线性波浪作用的分析。当波浪由深水区传至近岸浅水区域时，随着水深的减小，波浪的非线性特征不断增强，当近岸区的相对水深(即水深与波长之比)小于1/8～1/10时，线性波浪理论甚至Stokes非线性波浪理论已经不再适用，而需要采用椭圆余弦波理论对近岸浅水区的非线性波浪特征进行描述[9-10]。

因而，对于近岸浅水区，有必要对非线性波浪作用下溶质进入沉积物中的运移特征进行分析，以揭示波浪非线性特征对溶质运移过程的影响。本文基于Biot多孔介质理论和溶质运移的二维对流-弥散方程，建立了波浪作用下考虑沉积物变形效应的溶质迁移数值计算模型，通过数值模拟，对线性波，非线性二阶Stokes波以及一阶椭圆余弦波作用下的溶质迁移过程进行对比分析，以揭示波浪非线性对溶质进入沉积物迁移特征的影响。

1 数值计算模型

如图1所示，为波浪作用下海床溶质运移计算的几何模型示意图，坐标轴原点o位于海床面的左端点，x轴位于海床面，y轴以向上为正，波长为L，波高为H，水深为d，海床厚度h。海水-沉积物交界面处的溶质浓度为c0=1 mg·L-1；沉积物中的初始溶质浓度为cs0= 0。

1.1 海床表面波压力

(1)线性波

海床表面波压力方程为

(1)

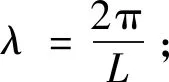
ω2=gktanh(λd)。

(2)

(2)二阶Stokes波

二阶Stokes非线性波在海床表面波压力方程式为[12]：

Pb(x)=P0(C11cos(λx-ωt)+C02+C20cos2(λx-ωt)+C22cos2(λx-ωt))。

(3)

式中：

(3)一阶椭圆余弦波

一阶椭圆余弦波在海床表面的波压力解析式为[13]：

(4)

1.2 渗流场控制方程

基于Biot弹性多孔介质固结理论[14]，考虑沉积物的变形与孔隙水渗流的耦合效应，控制方程如下：

(5)

(6)

(7)

(8)

β为孔隙流体压缩系数，表达式为[15]:

(9)

式中：Kw为孔隙水体积压缩模量，数值为2×109Pa；Sr为饱和度；pw0表示绝对孔隙水压力。

由达西定律，孔隙水在水平和竖向的实际渗流速度u、v分别为：

(10)

1.3 溶质运移方程

依据质量守恒定律，多孔介质中溶质二维对流-弥散方程为[16]：

(11)

(12)

(13)

(14)

1.4 边界条件与初始值

结合图1所示的几何模型示意图，数值模型的边界条件如下。

在海床表面y=0位置，土体的剪切力和有效正应力均为零；海床面的孔隙水压力为波浪在海床表面的波压力Pb(x)，根据需要可分别为线性波、二阶Stokes波和一阶椭圆余弦波的波压力，从而可以对不同类型波浪场作用下的海床渗流场进行计算；溶质在海床面上的浓度c(x,0,t)=c0=1 mg·L-1。

在海床底部y=-h处，为不透水边界，土体位移为0，即：

在海床两侧x=0和x=L处，为周期性边界，即：

p|x=0=p|x=L,wx|x=0=wx|x=L，

wy|x=0=wy|x=Lc|x=0=c|x=L。

此外，由于砂土海床的渗透系数较小，沉积物中的渗流符合达西定律，其对波浪场的影响较小[18]，故不考虑多孔介质海床对波浪场的影响。

2 数值模型验证

2.1 非线性波浪计算结果验证

通过与波浪试验结果的对比，验证本文非线性波计算结果的正确性。首先对非线性Stokes波的结果进行验证，如图2(a)中所示，为解析解计算的海床面波压力与Qi等[19]波浪水槽试验测试的海床表面波压力对比图，相应的波浪参数为H=0.095 m，T=1.2 s，d=0.5 m，由图可知，Stokes非线性波的计算结果与试验结果吻合较好，验证了本文Stokes波计算结果的正确性。其次，对一阶椭圆余弦波的计算结果进行验证，如图2(b)中所示，为一阶椭圆余弦波理论计算得到的波浪自由面高程与Chang等[20]试验记录的椭圆余弦波自由面数据对比图，其中波浪周期T=2.0 s，相对波高H/d=0.15，水深d=24 cm，波长L=2.97 m；图中试验数据为距离造波板4.8 m位置处测量的椭圆余弦波的自由面高程，可以看出本文解析解计算结果和试验结果一致性较好。综上可知，本文基于非线性波浪理论计算得到的结果正确，能够反映波浪的非线性特征。

2.2 渗流计算结果验证

Hsu和Jeng[15]基于Biot固结理论，考虑了海床土体的变形效应，推导了波浪作用下海床瞬态响应的解析解。将本文数值计算结果与该解析解进行对比。基本参数为：波高H=5 m，波长L=121.19 m，水深d=20 m，周期T=10 s，孔隙率n=0.333，泊松比μ=0.35，剪切模量G=5×106Pa，海床厚度h=25 m。对比结果如图3所示，图3(a)为不同渗透系数下孔压响应对比；图3(b)为不同剪切模量下孔压响应对比。从图3中对比结果可以看出，数值计算结果与解析解一致性较好，表明当前模型能够较准确地模拟波致海床的渗流场。

2.3 溶质运移计算结果验证

Packman等[21]基于砾石底床，通过水槽试验探究了不同水力条件下上覆水体中的溶质进入砾石床的情况，得出了上覆水体中溶质浓度随时间的变化曲线。将本文数值模型计算的溶质运移结果与试验结果进行对比。分别选取试验工况7和工况9的结果进行比较，计算参数为：孔隙率n=0.38，平均颗粒粒径dg=0.6 cm，渗透系数k=0.15 m·s-1，沉积物厚度为0.19 m，工况7中水深d=20.4 cm，波长L=32 cm，波高H=2 cm；工况9中水深d=20.4 cm，波长L=32 cm，波高H=3.76 cm。对比结果如图4所示，可以看出，数值模型的计算结果和试验测试结果较为一致，表明了本模型用于溶质运移计算结果的可靠性。

3 结果分析与讨论

随着波浪向岸传播，水深逐渐变浅，波浪非线性特征逐渐增强。当波浪Ursell数(其计算表达式为HL2/d3)大于40时[22]，椭圆余弦波理论能更有效地表达浅水非线性波浪的特征。为了更好地分析波浪非线性对海底沉积物中溶质运移特征的影响，同时对线性波浪、二阶Stokes波和一阶椭圆余弦波作用下溶质进入沉积物的过程进行数值模拟，具体计算参数见表1。波浪的Ursell数为43，属于典型的浅水非线性波浪。

3.1 波浪非线性对渗流场特征的影响

溶质运移特征主要取决于渗流场特征，因此，首先对不同类型波浪作用下沉积物中的渗流场特征进行分析。

如图5所示，为3种波浪理论下海床表面的波压力分布图，从中可以看出，线性波在波峰和波谷处的波压力绝对值相等，相对于静水位面对称；非线性波的波峰和波谷相对于静水位面呈现明显的非对称性，波峰处波压力增加，波谷位置的波压力降低。一阶椭圆余弦波的非线性特征相对于二阶Stokes波更加明显，一阶椭圆余弦波和二阶Stokes波在波峰处的波压力分别为线性波波压力的165%和120%，而在波谷位置二者的波压力基本一致，均为线性波波压力的80%。

表1 基本计算参数Table 1 Parameters for the base case

如图6所示为线性波作用下一个周期内不同时刻的孔隙水流速矢量图和等值面图。由于海床面不同位置存在水头差(压力差)，因此在海床内部会发生渗流，如图6中所示，波峰处发生向下的渗流，波谷处发生向上的渗流；对于同一位置，其渗流流速的数值和方向随着波压力的变化呈现出周期性变化。以海床表面任意点处的渗流为例，如图7中所示，竖向和水平向的渗流流速均随时间呈现出周期性变化，受波浪非线性的影响，一阶椭圆余弦波作用下波峰处的竖向渗流流速与波节点附近的水平向渗流流速均显著大于线性波和二阶Stokes波；总体而言，线性波和二阶Stokes波的流速数值相差较小。对3种波浪作用下沉积物和上覆海水之间的水量交换进行分析可知，无论是哪种波浪，一个周期内流入和流出沉积物的水量基本相同，即沉积物和上覆海水之间水的净交换量为0，因此，正如Harrison等[2]所述，在周期性循环波浪荷载作用下，对流作用对溶质质量运移的贡献基本可以忽略，波浪主要通过机械弥散作用促进溶质在沉积物中的运移。

3.2 波浪非线性对溶质运移特征的影响

一阶椭圆余弦波作用下周期平均纵向水动力弥散系数的增大，促进了溶质在沉积物中的运移。如图11中所示，在同一深度，一阶椭圆余弦波作用下的溶质浓度大于线性波作用下的溶质浓度，表明一定条件下的浅水非线性波可以促进溶质在沉积物中的运移。进入沉积物中的溶质质量随波浪作用时间的变化如图12中所示，从中可以更为清楚地看出，一阶椭圆余弦波作用下进入沉积物中的溶质质量明显大于线性波，3 000个波浪周期作用后，质量增加量可达线性波的7.2%。另外，从图11和12均可以看出，二阶Stokes波作用下溶质浓度的分布以及进入沉积物中的溶质质量均与线性波作用下的结果一致，表明二阶Stokes波的非线性效应对溶质运移过程的影响很小，基本可以忽略。上述模拟结果的分析表明，一阶椭圆余弦波非线性特征较强，能显著促进溶质在海底沉积物中的运移；相比之下，二阶Stokes波的非线性特征相对较弱，其对溶质运移过程的影响相对小。

3.3 波浪参数影响分析

3.3.1 波高的影响 根据前述内容可知，可以通过分析不同波浪参数对孔隙水渗流流速和溶质纵向水动力弥散系数的影响规律，来反映其对溶质运移的影响规律。Ursell数的大小表征了波浪非线性特征的强弱[13]，因此，基于Ursell数的变化来分析波浪非线性特征强弱的变化。

对一阶椭圆余弦波和线性波作用下波高对孔隙水竖向渗流流速和水动力弥散系数的影响进行对比，结合波浪的非线性特征，以分析不同波浪理论下波高对溶质运移过程的影响。波高H的取值分别为2、2.5和3 m，其余参数见表1中所示。

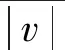
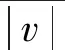
4 结论

以二阶Stokes波和一阶椭圆余弦波为例，通过与线性波作用下沉积物中孔隙水渗流场和溶质浓度场计算结果的对比，分析了波浪非线性对非反应性溶质从上覆海水进入沉积物中运移特征的影响，主要得到以下结论。

(1) 在周期性循环波浪荷载作用下，沉积物中的渗流场呈现出周期性循环特征，对于平底海床，波浪主要通过机械弥散作用促进溶质沿沉积物深度方向的迁移，一个波浪周期内的平均纵向水动力弥散系数可以用来表征溶质运移速率。

(2) 二阶Stokes波的非线性特征对溶质运移的影响基本可以忽略；一阶椭圆余弦波的非线性特征显著，能在一定程度上促进溶质在沉积物中的运移，与线性波相比，其周期平均纵向水动力弥散系数的增加量可达28%。

(3) 线性波和一阶椭圆余弦波作用下，波浪参数对溶质运移速率的影响不尽相同。随着波高增大，两种波浪作用下溶质运移速率均有所增加；随着水深的增大，线性波作用下溶质运移速率降低，而一阶椭圆余弦波作用下溶质运移速率增加；随着周期的增大，线性波作用下溶质运移速率增加，而一阶椭圆余弦波作用下溶质运移速率降低。

(4) 一阶椭圆余弦波的非线性特征随着水深的减小、波高和周期的增大而增强；与线性波相比，一阶椭圆余弦波的非线性特征对溶质运移速率的促进程度随着水深的减小、波高和周期的增大而降低。