回归模型在降水量空间分布格局中的应用

张中月 吴长悦 郑浩

(华北理工大学，河北 唐山 063210)

近百年来，全球气候变暖对自然生态和人类生存环境产生了显著影响，各种极端天气及灾害事件不断增加，给人类的生产生活和经济发展带来严重影响[1,2]。其中降水也是极其重要的,并且对人类生活与经济有着重要的影响。作为气候变化的基本要素之一，降水是一种复杂自然事件，在时间和空间上都表现出显著的多变性[3,4]。作为陆地水循环的重要组成部分，降水不仅是陆地表面重要的水源补给，还对土壤-水分状态密切相关的生态系统和农业生产力、水分和温度状态函数关联的生物地球化学过程以及依赖于水资源可持续性经济系统的功能等具有重要的作用[5,6]。本文以甘肃省为例，基于MTALAB软件研究多元回归模型在降水量空间分布格局中的应用。

1 数据与方法

1.1 数据

本实验共获取了甘肃省53个气象台站的经度、纬度、海拔、多年的年降水量以及年蒸发量的平均数据，选取其中43组数据，作为模型建立的基础数据，将剩余的10组数据作为验证数据以验证模型精度。

1.2 方法

1.2.1 归一化处理

本研究为消除指标之间的量纲影响，对降水数据集标准化处理，以解决数据指标之间的可比性，使原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。归一化处理的2种常用方法包括Z-score标准化方法和min-max标准化方法。本文使用min-max标准化方法也称为离差标准化，是对原始数据的线性变换，使结果值映射到[0-1]之间。转换函数如下：

(1)

式中，max为样本数据的最大值；min为样本数据的最小值。

对选定的43个气象台站的样本数据，利用式(1)进行归一化处理，将原始数据归一化为[0，1]之间的无量纲数据。

1.2.2 相关分析

相关分析的任务，是揭示地理要素之间相互关系的密切程度。而地理要素之间相互关系密切程度的测定，主要是通过对相关系数的计算与检验来完成的。

相关系数的计算：

(2)

表1 相关系数与相关程度关系

1.2.3 多元线性回归分析

1.2.3.1 多元线性回归模型的建立

多元线性回归模型的结构形式如下[7]：

ya=β0+β1x1a+β2x2a+…+βkxka+εa

(3)

式中，β0，β1，…，βk为待定参数；εa为随机变量。

如果b0，b1，…，bk分别为式(3)中β0，β1，β2，…，βk的拟和值，则回归方程为：

(4)

在式(4)中，b0为常数，b1，b2，…，bk称为偏回归系数。偏回归系数的意义是，当其自变量都固定时，自变量xi每变化一个单位而使因变量平均改变的数值。

1.2.3.2 多元逐步回归分析

逐步回归是一种通过添加或删除预测变量来构建模型的方法，通常通过一系列F检验或T检验。根据估计系数的检验统计量选择要添加或删除的变量。以确保每次引入新的变量之前回归方程中只包含显著性变量。

2 多元线性回归分析

2.1 年降水量及蒸发量相关性分析

将甘肃省各气象台的经纬度以及海拔数据作为自变量，降水量和蒸发量作为因变量。可以利用式(2)对降水量(p)和经度(x)、纬度(y)、海拔(a)之间的相关系数以及蒸发量(v)和经度(x)、纬度(y)、海拔(a)之间的相关系数进行计算，结果见表2。

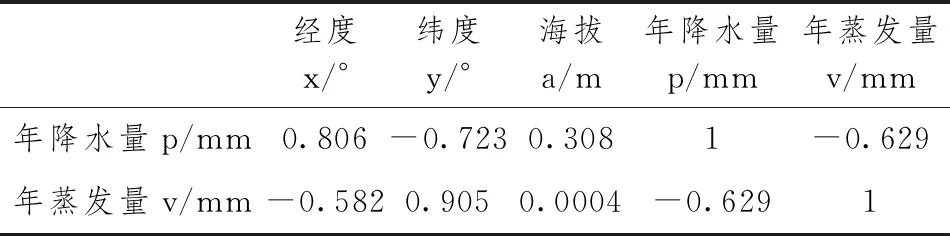
表2 气象台站的降水量、蒸发量与经纬度、海拔的相关性

结合表2与表4分析可得到年降水量(p)与经度(x)高度相关；与纬度(y)和年蒸发量(v)显著相关，且呈负相关；与海拔(a)间存在实相关关系。年蒸发量与纬度(y)呈正相关，与经度(x)和年降水量呈负相关；与海拔之间相关性仅为0.0004，相关性微弱，可忽略不计，与经度(x)实相关，与年降水量(p)显著相关，与纬度的相关性高达0.905，两者高度相关。

2.2 年降水量影响因素分析

因为年降水量与经纬度、海拔、年蒸发量都具有一定的相关性，因此将年降水量(p)作为因变量，将经度(x)、纬度(y)、海拔(a)以及年蒸发量(v)作为自变量建立多元线性回归方程：

p=β0+β1x+β2y+β3a+β4v

(5)

利用MATLAB软件中regress函数进行多元线性回归，得到降水量(p)的拟合方程：

p=0.7370+0.1625x-0.8659y+0.1531a-0.1510v

(6)

拟合方程的R2为0.8497，F统计量为53.7205，显著性P值为3.9317×10-15。

利用rcoplot(r，rint)绘制残差图，进行异常值剔除，异常值是指一组测定值中与平均值的偏差超过2倍标准差的测定值，与平均值的偏差超过3倍标准差的测定值，称为高度异常的异常值。建立循环函数对数据的异常值进行异常值剔除。得到最终的无异常值存在的35组数据，剔除过程如图1所示。

利用残差剔除后的35组数据再次建立多元线性回归模型，得到降水量(p)的拟合方程：

p=0.4280+0.4629x-0.6133y+0.1916a-0.0743v

(7)

拟合方程的R2为0.9210，是一个评价拟合好坏的指标，R2越接近1，拟合效果越好；F统计量为87.4911，显著性P值为4.28×10-16，F统计量用于判定模型中自变量X中是否至少有1个对因变量Y产生影响，如果呈现出显著性(看P值)，则说明所有X中至少1个会对Y产生影响关系。分析可得，年平均降水量(p)的拟合方程的拟合程度很高，且相较于残差剔除前的拟合效果提高显著。

利用异常值剔除之后的数据在显著性概率95%的条件进行多元逐步回归分析，筛选出满足显著性条件的参数。通过非参数检验将经度(x)、纬度(y)、海拔(a)以及年蒸发量(v)4个变量作为自变量赋值为X1、X2、X3、X4，以年平均降水量(p)作为因变量，对年平均降水量(p)的影响因素进行多元逐步回归分析，纳入标准为α=0.05。

多元逐步回归分析结果显示，参数X4(海拔a)不符合标准，F=119.224，P=4.1547×10-17，R2=0.9202，RMSE=0.0822。说明回归方程成立且拟合较好。影响年平均降水量的因素按其效应由大到小依次为纬度(y)、经度(x)、海拔(a)。多元回归分析结果如图2所示。

利用多元逐步回归分析的结果在regress中再次建立回归方程，求解参数，重新建立年平均降水量的拟合方程：

p=0.4134+0.4840x-0.6642y+0.2019a

(8)

2.3 显著性检验

采用方差分析法进行回归方程总体显著性检验。在MTALAB中利用regstats函数求解方程的F统计量为119.224，F检验的P值为4.1547×10-17。在给定的显著水平0.05下，按单尾检验法，以分子自由度3，分母自由度31为引数，查F分布表Fa为2.9113，可知F远大于Fa，总体回归效果显著，说明年平均降水量(p)和纬度(y)、经度(x)、海拔(a)之间线性相关可信。

参数显著性检验。在多元线性回归中，并不满足于回归方程是显著的这一结论，因为F>Fa只能说明方程总体的回归效果，但并不能排除某个β=0，所以还需逐一对参数的显著性进行检验。在MTALAB中利用regstats函数求解方程各参数的t统计量，见表3。

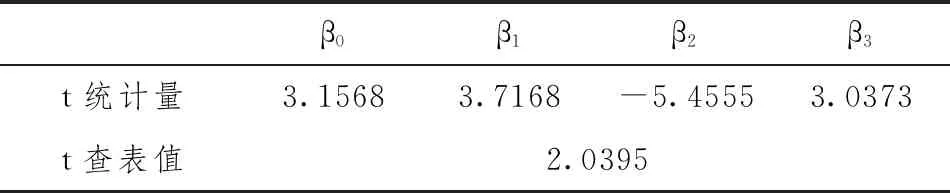
表3 各参数t统计量及查表值

查t分布表，在自由度为31时，t0.05=2.0395，显然t>tα，这表明在置信度水平α=0.05上，回归方程的系数β0、β1、β2、β3是显著的。

2.4 降水量预报值的区间估计

回归分析的一个主要目的是根据给定的x值对y值进行预报。甘肃省年平均降水量(p)的有效线性回归方程如式(8)所示，利用式(5)、式(6)计算归一化后的预报值的区间估计。并进行反归一化，得到年降水量的预报区间，选择10个气象台站的年平均降水量作为预报区间验证。验证数据及预报区间见表4。

表4 气象台站经纬度、海拔及降水量验证数据

表4的结果显示，10组数据的实际年降水量都在预报区间内，其中民勤气象台站的实际数据接近预报区间边缘，准确度较低。其余9组数据的预测可靠性较高。也证实了回归方程的拟合效果显著。可用于预测甘肃省不同经纬度、海拔的年平均降水量。

3 结论

本文对年降水量及蒸发量做相关性分析，得到年降水量及蒸发量与其他各参数间的相关程度。利用甘肃省各气象台站多年平均降水量作为因变量，以经度、纬度、海拔、年平均蒸发量作为自变量，建立多元回归模型。通过逐步回归剔除了年平均蒸发量，筛选出满足显著性0.95以上对多年平均降水量的影响程度为纬度>经度>海拔。所建立的模型计算结果精度较高，对甘肃省年平均降水量的空间分布格局的预测有一定的参考价值，对农业发展中不同季节降水量有着预测作用。