空域滤波图像去噪算法研究
2022-11-16邢笑笑李杰
邢笑笑 李杰
(商洛学院 陕西省商洛市 726000)
在许多领域和应用中,图像的使用越来越受欢迎,如在医学、教育、军事和航天航空等领域,但是噪声的污染可能会存在于图像的获取、传输、接收和处理等过程中。噪声的存在会使图像的视觉效果降低,也会严重影响图像的边缘结构信息,对图像的后续处理和分析有极大影响,如图像风格转换、边缘提取和特征匹配等。因此,在实际的图像处理过程中对图像预先进行去噪处理是非常重要的。
在图像处理领域,国内外众多研究学者致力于研究图像方面的去噪处理,如今已经有许多具有代表性的去噪算法产生。现有的滤波算法按照处理域的不同,可以分为频域滤波和空域滤波。频域滤波是通过某种变换将图像从空间域变换到变换域,然后再进行处理,最后将处理好的结果逆变换到空间域。主要方法有低通滤波、高通滤波、小波变换等[1,2];空域滤波是对图像中的像素值直接进行处理,典型的算法有均值滤波、中值滤波和高斯滤波等[3‐5]。为了获得更好的去噪性能,不断有新的理论和新的方法涌现,1998年Tomasi 等[6]人在高斯滤波的基础上再结合邻域滤波提出了一种新的滤波算法—双边滤波,该方法中权值的确定是根据像素与像素之间空间上的邻近性和灰度上的相似性。2005年Baudes 等[7]人提出了非局部平均去噪算法(NLM:Non‐local Means Denoising Algorithm),该方法利用图像中所有像素点与待处理像素点之间的灰度相似性进行加权平均来估计像素值,该方法取得了较好的去噪效果。NLM 的提出开启了去噪算法研究的新思路,后续有许多学者根据NLM 滤波提出了一系列的改进算法[8‐10],2007 年Dabov 等[11]人利用图像之间存在的相似性对图像在频域里面进行处理,主要是对具有相似结构的图像块进行,其中块估计值是通过逆变换得到的,然后再把得到的块估计值放到空间域中,最后对图像中有重叠的块估计进行加权平均得到最终的去噪效果图。2010 年何凯明等[12]人利用一幅引导图像对待处理的加噪图像进行滤波处理,滤波后得到的输出图像在纹理上与引导图像相似,大体结构上与加噪图像相似,该方法称之为引导滤波。2014 年zhang 等[13]人提出了一种滚动引导滤波,该方法利用联合双边滤波器作为框架的边缘恢复滤波器,可有效的滤除噪声,并且保持图像的边缘信息。
稀疏编码是近年来流行的一种降噪技术,在稀疏表示方法里面构造合适的字典是其中一个重要的环节。该类方法里面最典型去噪算法有离散余弦变换[14]、全局字典[15],基于过完备字典的稀疏表示[16,17]。在变换域里面过完备字典的稀疏表示方法是一个重要的方向,2006 年Aharon 等人提出了一种K‐SVD(K‐Singular Value Decomposition)算法,该方法主要是在当前字典的实例稀疏编码和更新字典原子之间交替进行,其中更新字典原子是为了更好地拟合数据,最后将更新的字典列和更新的稀疏表示相结合,以此来加快收敛速度。这种方法的自适应性能力非常强、算法过程简单同时取得了较好的去噪效果,因此引起了许多研究学者的广泛关注和继续探索[18‐20]。
1 经典的去噪算法
1.1 均值滤波
图像中原有的像素点与像素点之间都具有相似性,而噪声点与其周围像素之间是不相似的,这是因为噪声的灰度值都是孤立存在的。即图像中的噪声是随机噪声。因此可以采用求平均的方法得到去噪后的像素值,来减弱或者消除噪声。均值滤波的输出为邻域内所有像素之和的平均值。首先选取一定大小的图像块,作为滤波的模板W,将模板里面点的系数都设为1,然后在噪声图像中以待处像素为中心选取与模板大小相同的邻域,对其进行模板卷积。

其中Ωi为图像g 中以i 为中心,半径为r,N×N 大小的方形区域,与模板W 所覆盖的范围对应;M 为Ωi内所有像素的个数。
1.2 中值滤波
在图像中,椒盐噪声和干扰脉冲一般以孤立点的形式出现。这些噪声或干扰在整幅图中所占的像素较少。中值滤波可以将图像中的噪声或干扰去除掉,同时又能使图像中的边缘结构信息得以保留。中值滤波属于一种非线性滤波,是基于模板排序来实现的,该方法将待处理像素点作为中心,确定一定大小的方形区域,即模板,然后将这个模板里面的像素值按大小顺序进行排序,取排序结果的中间值代替初始图像中待处理像素点处的值。

其中Ωi表示以像素点i 为中心,N×N 大小的方形区域;i,j∈Ωi。对于一幅图像,中值滤波的模板是待处理像素为中心的方形区域。一般情况下中值滤波模板中像素点的个数取为奇数,以保证有一个中间值,滤波模板可取为3×3,5×5 等。而若设置Ωi内像素点个数为偶数时,则选取两个中间值的平均值作为中值。
1.3 高斯滤波
一般情况下污染图像的噪声都是高斯噪声,因此很多场合中都是使用高斯滤波器进行去噪的,该滤波方法可以有效地抑制噪声,平滑图像。在线性平滑滤波中高斯滤波是具有代表性的滤波算法,高斯滤波中根据高斯函数的形状来选取权值;由待处理像素点的灰度值和其邻域内其他像素点的灰度值的加权平均得到去噪后的像素值;高斯滤波器的模板系数随着距离中心像素的增大而减小。
在图像处理中,平滑滤波器经常选的是零均值离散高斯函数。高斯滤波就是利用输入图像g 和高斯函数进行卷积运算,可以表示为:
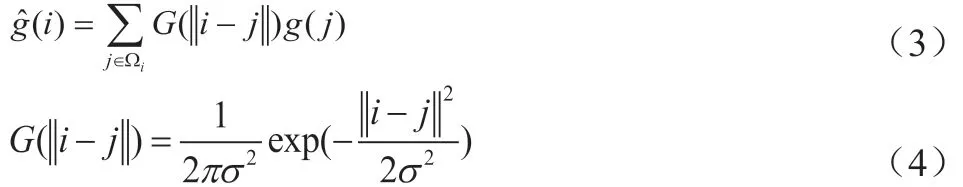
其中,G(•)表示二维高斯函数,Ωi表示以像素i 为中心的方形区域,g(j)表示方形区域Ωi内像素点j 处的像素值,表示滤波后像素点的灰度值,式(2‐5)中||i‐j||表示的是邻域内其他像素到邻域内中心像素的距离,σ 表示截止频率到频域中心的距离。
1.4 双边滤波
双边滤波是一种非线性的滤波方法,利用像素与像素之间在空间上的邻近关系和灰度上的相似关系共同来确定权值,这样在滤除噪声的同时又能保留边缘的细节信息。空域滤波计算空间域权重时,利用邻域像素值与目标像素值的距离;计算值域权重时,利用邻域像素值与目标像素值的差值。
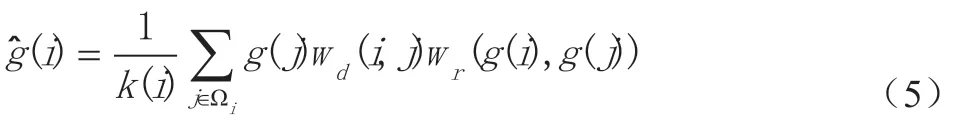
其中归一化因子为:
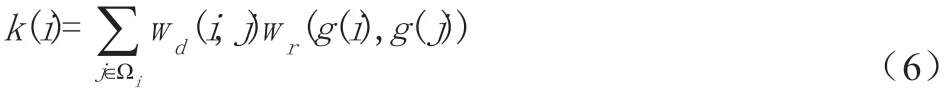
Ωi表示以像素点i 为中心的方形区域,j 表示该区域中的任一个像素点;邻域中心i 处的像素与附近点j 的像素之间的几何邻近性用wd(i,j)来表示,即在空间域滤波时g(i)处的权值;邻域中心i 处的像素与附近点j 的像素之间的灰度相似性用来表示,即在值域滤波时g(i)处的权值。
式(5)中邻近函数wd(i,j)和相似函数都是自变量之间欧氏距离的高斯函数,则邻近函数wd(i,j)可表示为:

其中

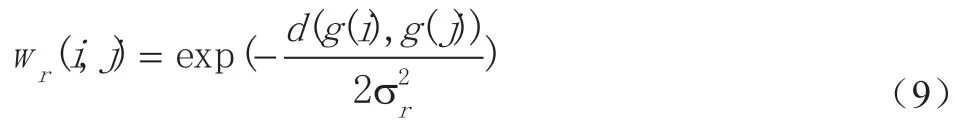
其中

是表示g(i)和g(j)之间的灰度值差;其中高斯函数的距离标准差用σd表示,它的选择主要是通过所需的低通滤波量;高斯函数的灰度标准差用σr表示。
2 两阶段非局部均值滤波算法
2.1 非局部平均去噪算法
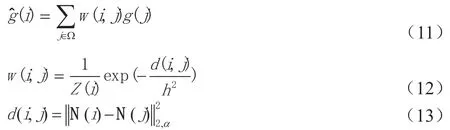
其中归一化因子Z(i)为:

N(i)、N(j)分别表示以像素i、j 为中心,大小为的图像块;权值族取决于图像块N(i)和N(j)之间的相似性,并且满足0 在非局部平均算法中,一般情况下参数h 与图像中所加噪声标准方差的取值一样,这时图像的结构和细节信息保持相对来说最好。而当滤波参数取值过大时,滤波后的图像会趋于光滑,不能很好的保存图像的细节信息,从而使得图像的去噪效果降低。因此,为了得到较好的去噪效果,设计了一种使用两次非局部均值滤波的方法,来解决NLM 算法中因取值过大而导致图像过于光滑的问题,从而提高图像的去噪效果。 在第一阶段滤波时,将滤波参数h1取值为标准方差的一半,每一个像素点都使用相同的滤波参数。而在第二阶段滤波时每个像素点上使用不同的滤波参数h2,h2的取值用前一次滤波的权值来计算。第一阶段滤波后每个像素点处噪声标准差的大小由该点处的权值决定,可表示为: 因此将σ2(i)作为第二阶段滤波时的滤波参数,即: 在第一阶段滤波中使用较小的滤波参数,因此只去除了一部分噪声,但同时保留了图像的细节信息,这样可以解决NLM算法中因滤波参数过大导致图像细节信息丢失的情况。而第二阶段滤波最主要的目的是去除上一阶段滤波没有去除干净的噪声,同时使图像细节信息的保持能力加强。 本文通过仿真实验来验证各算法的有效性,在MATLAB R2015b 仿真软件上进行。所有算法均加入的高斯白噪声标准差为σ=30,均值滤波和中值滤波中模板的半径为2,双边滤波中搜索窗口的半径取值也为2,非局部均值滤波和两阶段非局部均值滤波中搜索区域的半径为10,图像块的半径同样取值为2。本文采用图像去噪领域最常用的质量评价方法峰值信噪比(Peak signal to noise ratio,PSNR)和结构相似度[21](Sructural similarity,SSIM)来评价六种滤波算法去噪后的效果。 表1 给出了六种不同方法在相同噪声强度下的PSNR 和SSIM 的对比值。均值滤波和中值滤波和高斯滤波的去噪效果低于双边滤波,而非局部均值滤波的效果又优于双边滤波,同时两阶段非局部均值滤波相较于非局部均值滤波的去噪效果要好。 表1:六种滤波算法的PSNR 与SSIM 值 选取图像去噪研究中常用的Lena 图像作为测试图像对六种典型的滤波算法进行去噪效果对比,如图1 所示,(a)和(b)分别为原图和加噪图像。对加入高斯白噪声的图像分别进行滤波处理,得到一组滤波后的图像。如图3 中c‐h所示,分别是六种滤波算法去噪后的图像。可以看出,随着图像滤波方法的深入研究,其视觉效果在不断地提高。 图1:六种经典算法的去噪效果对比图 均值滤波是一种最简单的图像平滑算法,该算法计算速度快,方法简单。但是其处理效果与模板的大小有关,模板的尺寸越大,则图像的模糊程度也越大。 中值滤波可使与周围像素灰度值差别比较大的像素点(噪声像素)改为与周围像素值接近的值,以此来消除孤立的噪声像素。中值滤波相比于均值滤波对于椒盐噪声的去除有很好的效果,同时能较好的保持图像的边缘细节信息。但它不适合用于处理含有丰富细节纹理的图像,特别是包含比较多的点、线、尖顶细节等的图像。 高斯滤波对于均值滤波而言,可以更好地去除图像中的噪声。在高斯滤波中实现距离的逼近,通过对像素点处的灰度值与随距离值改变的系数进行加权。一幅图像中两个像素不仅可以彼此接近,也可以彼此相似。而高斯滤波中高斯核只考虑了像素值的空间分布,而未考虑两个像素之间的相似性,使图像的细节边缘被模糊掉。 双边滤波器主要针对高斯滤波器所产生的模糊问题而提出的,它能更好地消除噪声,并且可以保留图像边缘的细节信息。但是当噪声图像边缘的一个像素周围有多个相似像素时,计算得到的高斯加权平均权重会不稳定。在这样的情况下,滤波后效果图的边缘处会出现光晕。双边滤波存在的另一个不足之处是运行效率,算法的运行效率低,花费时间长。 非局部均值滤波是空域滤波算法中的一个里程碑算法,该方法的提出解决了之前局部方法中存在的缺陷,它充分地利用了自然图像中存在的大量冗余信息,更好地保留了图像的细节和纹理。该方法具有算法简洁、性能优越、易于改进和扩展的优点,但是算法运行效率低,时间复杂度高。主要是算法在计算两个图像块之间加权欧氏距离时,存在大量的重复计算。 两阶段非局部均值滤波使用两次滤波方法,每次滤除少量的噪声同时尽可能多的保留图像细节信息,从而解决非局部均值滤波里面因为滤波参数取值过大而造成图像结构和细节信息丢失的现象,提高图像的去噪效果。该算法使用的是两阶段滤波的方法,同时第一次滤波参数的取值是噪声标准差的一半,但是在两阶段非局部均值滤波算法里面进行几阶段的滤波,第一阶段滤波参数的取值如何选取最合适,都没有进行具体分析,这有待于后续的研究。 本文介绍了六种具有代表性的空域滤波方法的性能及其优缺点,并通过仿真实验对测试图像分别进行滤波处理。通过仿真实验可以得出,前期的图像去噪方法在滤除噪声和保持图像的边缘信息上往往不能兼顾,但随着学者们的不断研究,图像在去噪的同时,保留图像的边缘信息上有所提高。近年来,基于深度学习的图像去噪方法被提出并得到了发展,但是深度学习需要大样本进行训练以及非常高的运算能力。今后的主要研究方向可将深度学习方法与传统的图像去噪方法相结合,以此来取得更好的去噪效果。2.2 两阶段非局部平均图像去噪
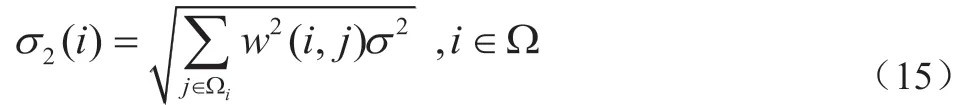
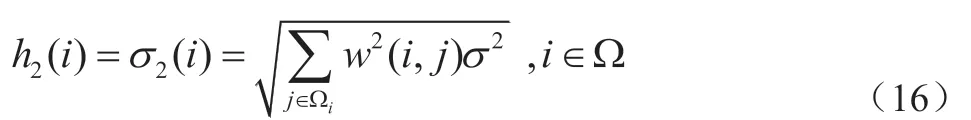
3 实验结果分析


4 结束语
