一种新研航天器系统可靠性指标论证方法

周文明 李彩霞 廖捷 李孝鹏 李一钊 张桅 段加林

(1 中国航天标准化研究所，北京 100071)(2 中国运载火箭技术研究院，北京 100076)(3 中国航天员科研训练中心，北京 100094)(4 北京空间飞行器总体设计部，北京 100094)

新研航天器系统可靠性指标论证和最终确定是使用方和系统承研单位共同权衡协调得到的，航天器系统可靠性指标论证过程就是系统可靠性指标确定过程。国内相关行业开展了大量的装备级、系统级的指标论证工作[1-5]，可以说系统可靠性指标确定是开展实施可靠性相关工作的基础和开端，也是系统开展研制、试验及验证的主要依据。对于时间跨度较大的重大工程(如载人航天工程)，涉及多阶段多任务模式的航天器系统研制，除了系统可靠性设计要求值外，不同研制阶段应验证的系统可靠性指标也应当予以明确。多研制阶段多任务模式的系统可靠性指标不合理会造成职责不清，阶段检查及验证标准不明确，甚至会导致执行系统质量与可靠性管理工作困难[6]。在工程实际中，依然存在着可靠性指标越综合概念越抽象，使用方和系统承研单位职责模糊，系统各层级指标关联度不高致使指标落实遇到困难等；而且，传统用单一顶层指标来指导航天器系统研制及验证工作的观念，会导致工程不同实施阶段航天器系统顶层验证指标的缺失，影响系统相关设计及各阶段验证评估工作。因此，需要在新研航天器论证初期就提出一套相对完整的系统可靠性指标体系。

在我国航天器研制中，通常给出系统正向可靠性指标要求，在指标论证过程中主要采用可靠性框图(RBD)方法进行模型构建、分析和论证。经过多年的研究和工程应用，一些国家(如美国)已经形成了一套规范完整的可靠性论证方法，并且开发了相应的标准规范和软件工具[7-11]。NASA在早期阿波罗计划中主要采用RBD方法对可靠性指标进行论证，在载人探索体系中，相关研究团队则采用概率风险评估(PRA)方法分析了执行各种设计参考任务(DRM)的数百种不同发射组合方案。其中，PRA方法的核心思路是事件链建模和故障建模[12]。传统做法是利用RBD方法和PRA方法给出航天器单一的系统顶层指标，并在系统顶层指标基础上逐次对系统层指标进行分解。然而，对于复杂航天器而言，在工程任务实施不同阶段存在不同的任务模式，任务方案和架构也可能会随工程规划计划安排不断迭代更新，这就会导致单一的系统顶层指标无法满足航天器研制全周期的指标落实和验证工作，对一些研制周期跨度大的工程任务来讲，工程实施各阶段采用单一指标回答航天器系统可靠性水平，需要很多试验、验证假设，这会给系统承研单位带来很多困扰，尤其在研制任务初期没有累积大量试验数据的情况下，需要对未来试验情况进行假设，才能回答指标的符合性。

针对上述情况，本文基于新研航天器可靠性指标论证工作特点，提出了一种可靠性指标论证方法，可为可靠性指标从航天器工程顶层任务规划、系统、分系统至单机综合权衡优化提供一套解决方案，既适用于新研航天器系统可靠性指标论证工作，也能从可靠性角度为工程整体的任务规划提供依据。

1 可靠性指标论证方法

传统用单一顶层指标指导航天器系统研制及验证工作，在分阶段实施的重大工程项目中，会导致工程不同实施阶段航天器系统顶层验证指标的缺失，影响系统相关设计及各阶段验证评估工作。结合新研航天器指标论证工作特点，采用分阶段提出验证指标(这里是指工程任务特定阶段末期航天器系统需回答并验证的阶段可靠性指标要求，即阶段可靠性指标门限值)的方式为航天器系统承研单位开展试验规划、试验方案设计、试验大纲编制等提供科学依据，避免从未来找试验数据、通过假设数据来验证当前阶段系统可靠性能力的问题。新研航天器系统可靠性指标论证方法具体包含4个步骤。

(1)可靠性指标初步论证。根据国内外相似航天器的可靠性指标论证工作实施情况，针对新研航天器系统典型任务剖面，开展系统可靠性指标初期论证，得到系统层可靠性目标值初值，即可靠性设计要求值，作为系统开展初期设计论证工作的依据。一般，进入系统方案设计阶段之前需要明确可靠性设计要求值，作为系统后续研制工作的输入。

(2)系统全任务周期可靠性增长趋势图确定。结合工程任务规划，依据初期论证的系统可靠性指标开展本系统可靠性指标论证工作，对本系统完成指标的技术能力水平进行预估，并给出当前能力下达到可靠性目标值初值可能的系统全任务周期可靠性增长趋势图，即系统成功飞行次数与系统可靠性变化趋势图。需要指出的是，任意一次飞行任务的失败都反映出系统设计、生产、组装或使用某环节存在重大质量问题，很可能导致研制进度的延迟甚至是研制任务的取消。

(3)基于可靠性指标的工程任务规划权衡分析。根据工程任务规划权衡分析系统可靠性指标满足程度，结合系统现有技术能力水平和系统全任务周期可靠性增长趋势图，以最大包络方式，在确保飞行次数可验证系统可靠性水平的基础上，给出任务规划调整方向并确定工程飞行任务实施类别和次数。

(4)系统可靠性指标目标值(设计要求值)和门限值(阶段可靠性指标门限值)确定。根据调整后的任务规划，采用基于任务剖面链思想开展整个系统的可靠性指标确定工作，明确系统可靠性指标的目标值和门限值。

1.1 系统可靠性指标初步论证

复杂航天工程包含多个实施步骤，每个步骤又包含多项飞行任务。例如，我国实施载人航天工程确定“三步走”的发展战略目标，并就各步骤具体任务进行明确[13]。对于新实施的航天工程来说，明确实施步骤和目标，确定各步骤应开展的任务是开展工程相关系统可靠性指标论证的前提，也是后续工程规划和任务计划权衡优化的基础。

开展航天器系统可靠性指标初期论证，首先应当明确所处工程设计参考任务、基线任务方案和架构，据此进一步分析确定航天器系统任务最大包络——典型任务剖面，用于系统可靠性指标论证工作。在得到典型任务剖面后，构建不同飞行任务模式下的航天器系统任务剖面链模型。对于新研航天器系统而言，需要在典型任务剖面链模型的基础上，根据国外相似航天器的指标论证情况和国内有关航天器数据开展系统不同飞行任务模式下可靠性指标确定工作，在收集相似航天器数据基础上开展系统自身技术水平和能力的评估，得到在当前技术水平下系统可靠性指标。航天器系统总体单位组织相关承研单位开展系统及以下各层级产品的可靠性指标综合分析，并在任务剖面链分析的基础上得到系统可靠性目标值初值，多方协调后得到系统可靠性指标初步论证结果，将该初值逐级分解并下发至分系统各级承研单位指导开展分系统初期设计论证工作。图1给出了系统可靠性指标初步论证基本过程，可以看出，工程设计参考任务分析、系统典型任务剖面确定及任务剖面链模型构建是开展系统可靠性指标初步论证的基础。为了更加合理地提出可靠性设计指标，需要广泛调研国内外相似航天器相关信息。在利用国外数据信息进行可靠性指标初步论证时，考虑到国外数据的不可获得性，需要根据实际情况，应增加利用国内航天器数据开展论证工作。

图1 新研航天器系统可靠性指标初步论证过程

基于任务剖面链的可靠性指标论证模型构建，是在PRA方法(事件链建模和故障建模)的基础上结合当前我国航天器可靠性指标工作实际需求提出的。基于任务剖面链的可靠性指标论证基本过程如下。①根据工程任务规划、飞行任务类型、飞行模式及确定的设计参考任务，并在设计参考任务基础上，确定航天器系统典型任务剖面；②结合工程实施步骤、目标及飞行任务模式等，结合典型任务剖面采用PRA方法给出不同飞行任务模式下的航天器系统任务剖面链模型；③基于工程典型任务的任务剖面链模型开展航天器系统指标的确定工作；④得到工程典型任务剖面下的系统可靠性指标，即系统可靠性设计要求值；⑤根据不同飞行任务模式下的任务剖面链模型，结合典型任务剖面链模型及数据，给出不同飞行任务模式下的系统可靠性指标。

1.2 系统全任务周期可靠性增长趋势图确定

根据航天器系统可靠性指标初步论证结果，对比分析工程各实施步骤不同飞行任务模式下的系统可靠性指标，并根据工程实施步骤给出系统可靠性指标的增长趋势图。

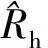
(1)

式中：系统先验的等效任务成功数sh=nh-rh。

(2)

在得到任务可靠度标准差后，可以对任务可靠度进行归一化处理，使其近似服从标准正态分布，则按式(3)可以得到归一化后的统计量，置信度为(1-α)×100%的置信区间如式(4)所示。

(3)

(4)

式中：±zα/2为正态分布双侧区间分位点；α为显著性水平。

若α=0.3，则0.7置信度下的任务可靠度下限为

(5)

假设航天器系统执行正式飞行任务前需要完成多次试验飞行任务，试验飞行任务分为2种类型，按时间顺序分别为试验飞行任务A(NA次)和试验飞行任务B(NB次)，当顺利完成各次试验飞行任务后，方能执行正式飞行任务，且执行正式飞行任务前，航天器系统满足规定的系统可靠性设计指标要求。

在得到NAdd次等效试验飞行任务数据后，假设航天器系统通过试验数据累积条件下的可靠性增长能力满足均匀分布模型，且系统试验时间在研制和试验飞行任务实施周期Td，t内等分，则可以将NAdd次试验飞行转换成Td，t研制周期的可靠性设计及验证能力，则每年等效试验飞行次数为

Nann=NAdd/Td，t

(6)

若研制周期为Td，则首次试验飞行任务A前应完成等效飞行试验次数为

Nd=Nann·Td

(7)

等效飞行试验失败次数(即研制周期Td结束后等效飞行试验失败次数)为

rd+=rh

(8)

同样，可以得到首次试验飞行任务B前应完成等效飞行试验次数为

N-B=nh+Nd+NA-rA+

(9)

式中：rA+为试验飞行任务A的NA次试验飞行任务中出现任务失败的次数。

等效飞行试验失败次数为

r-B=rh+rA+

(10)

在已知先验信息基础上，结合系统等效成功试验飞行任务次数后验信息，可以绘制系统可靠度随飞行任务成功次数变化曲线，从变化曲线中可以看出系统随成功试验次数增加的可靠性增长趋势，同时可以得到已知先验信息、在当前试验能力及具体任务规划基础上首次试验飞行任务A、首次试验飞行任务B及执行正式飞行任务前的系统可靠性，即为研制及试验飞行任务期间规定阶段的系统可靠性门限值，可作为系统不同阶段末期可靠性验证指标，指导系统研制试验设计、飞行试验任务规划等工作。若存在飞行任务模式较多的情况，建议综合考虑工程任务特点、航天器研制过程及飞行任务模式，以任务剖面覆盖性作为依据，确定包含不同类型任务模式的最大包络设计参考任务模式。

1.3 基于可靠性指标的航天器任务规划权衡分析

在得到航天器可靠性指标设计要求值和不同阶段末期可靠性指标验证要求值(门限值)后，系统总体单位组织分系统及以下承研单位开展进一步论证分析，根据历史经验，确定系统关键分系统、关键单机等，并对关键分系统、关键单机的验证能力进行分析，确定关键分系统、关键单机的验证能力是否能满足不同阶段系统可靠性指标验证工作需求。当现有验证能力能够满足指标验证工作需求时，无需开展航天器飞行任务规划权衡分析；否则，需要适当调整研制周期和/或任务规划。

出现工程指标要求达不到的情况时，通过分析得到当前系统可靠性水平下系统进行几次飞行试验可以满足首次试验飞行任务A和首次试验飞行任务B可靠性指标要求；在此基础上，对航天器任务规划进行调整，明确为满足规定的指标要求系统研制周期时间跨度增加量、试验飞行任务A和试验飞行任务B应成功执行次数。

通常来说，新研航天器系统规划的飞行任务次数远远不能满足系统可靠性验证需求，需要开展大量的地面验证试验，采用金字塔法对系统可靠性水平进行估计，通过增加地面试验验证时间可以减少规划飞行任务次数的需求。图2给出了在系统可靠性指标设计要求值和门限值基础上开展系统任务规划分析权衡过程。涉及到可靠性指标目标值、门限值的提出，基于任务规划分析权衡技术的指标优化和任务规划迭代更新，以及指标合同值的提出和阶段性指标预估、评估等工作，同时也给出了系统可靠性指标论证、迭代更新与系统任务规划和研制过程的相互关系。

图2 基于可靠性指标的新研航天器系统任务规划分析权衡过程

从图2可以看出：在规划任务均能正确实施的前提下，通过基于可靠性指标的航天器任务规划分析权衡工作，可以得到更新后的任务规划。利用更新后的任务规划，能进一步分析不同飞行任务首次飞行前的可靠性指标要求。若在实际研制过程中某次试验飞行任务出现重大事故，则需要采用式(1)～(5)对系统可靠性增长趋势图进行更新，明确当前的任务规划和系统研制能力能否满足系统研制总的任务目标和需求，并应给出任务规划或系统研制计划进度调整的决策建议。当然，在实际工程中，如果重大事故完成了归零工作，相应设计更改也得到了充分验证，那么可以利用更改后数据结合剩余研制时间和任务规划中的飞行任务次数，对系统可靠性增长趋势图进行迭代。更新后的系统可靠性增长趋势图可以为系统研制计划进度安排提供决策支持。通过系统可靠性增长趋势图和系统及以下产品的研制进度情况，可以适时调整研制计划和具体工作安排。

1.4 工程可靠性指标目标值和门限值确定

根据明确后新的试验飞行任务A和试验飞行任务B，采用基于任务剖面链的方法开展系统可靠性指标论证和确认工作，针对首次试验飞行任务A、首次试验飞行任务B及首次执行正式飞行任务，分别给出系统可靠性指标的目标值和门限值。其中：目标值以执行正式飞行任务为典型飞行任务模式进行论证；基于试验飞行任务A和试验飞行任务B次数，采用贝叶斯方法计算得到首次试验飞行任务A、首次试验飞行任务B及首次执行正式飞行任务系统可靠性指标，作为门限值。因此，通过基于任务剖面链的方法开展工程各种飞行任务模式下的系统可靠性分析论证，可以得到航天器系统可靠性目标值和门限值，随着研制工作的推进，可将系统指标进一步分解到分系统直至单机部组件级，形成一套完备的可以指导后续系统及以下产品研制工作的可靠性指标体系。

为了避免航天器各层级设计人员处于开环作业的盲目地位，系统可靠性指标要求一旦确定就要转换为系统各层级的设计要求和生产要求。常用的方法是质量功能展开(QFD)，使用通常称为“质量屋”的工具，它是把使用方要求转换为功能要求、物理特性和过程控制的系统工具。

2 实例分析

假设某新实施工程任务包含试验飞行任务A(规划3次)、试验飞行任务B(规划2次)及正式飞行任务3种任务模式，涉及飞行器包括航天器系统S1、航天器系统S2及运载火箭系统。假设在工程论证阶段利用国内外数据得到典型任务模式(正式飞行任务)下可靠性设计要求值分别为0.980 0，0.958 3，0.958 3。采用基于任务剖面链的方法对试验飞行任务A、试验飞行任务B及正式飞行任务3种任务模式进行可靠性指标论证模型构建，得到3种飞行任务模式下可靠性指标论证任务剖面链模型，如图3所示。

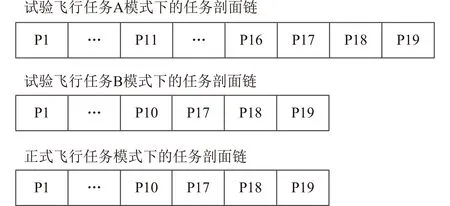
图3 任务剖面链模型

根据任务剖面链模型和各阶段任务失败概率，可以采用事件树仿真方法计算得到不同任务模式下的系统可靠度。其中：①各任务阶段可靠度主要通过建立阶段任务模型(通常为故障树)、收集相关历史经验数据开展阶段任务可靠性评估；②航天器系统各阶段任务可靠度则根据各阶段任务中系统参与情况，对阶段任务可靠性进行解耦，通过任务阶段中航天器系统关联关系及任务功能实现，构建阶段任务指标分解模型，计算得到航天器系统在各阶段任务可靠度；③利用航天器系统在各阶段参与情况及在各阶段任务可靠度，利用式(11)开展各系统任务可靠度计算。

(11)

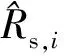
根据式(11)得到不同任务模式下的航天器系统可靠度。假设利用现有条件下相似航天器系统历史经验数据得到系统的可靠度不满足设计目标值要求，详见表1。从表1中假设数据可以看出：利用当前航天器系统S1、航天器系统S2及运载火箭系统具备的可靠性水平远远达不到进行正式飞行任务的要求，因此需要进一步分析任务规划，从任务可靠性角度明确在开展正式飞行任务前试验飞行任务A和试验飞行任务B执行次数；从任务可靠性角度明确第1次试验飞行任务B前试验飞行任务A执行次数，以及明确正式飞行任务前试验飞行任务A和试验飞行任务B执行次数。

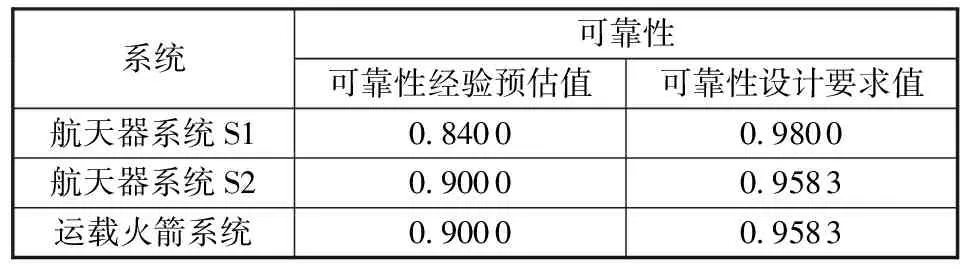
表1 基于历史经验数据的系统可靠性预估值及设计要求值

前述假设工程初期任务规划为试验飞行任务A成功执行3次和试验飞行任务B成功执行2次数后，开展正式飞行任务。采用正式飞行任务指标目标值初值数据，根据工程规划的飞行模式和飞行次数，并根据当前系统可靠性水平分析得到的实施第1次试验飞行任务A前的系统可靠性水平，采用贝叶斯方法计算首次试验飞行任务B实施前和正式飞行任务实施前的系统可靠性指标。以航天器系统S1为例，基于当前技术水平，试验飞行任务A可以达到的可靠性点估计值为0.840 0，可以认为25次试验飞行任务A有4次失败，则根据伯努利分布极大似然估计方法，采用式(1)～(5)计算可知，当前航天器系统S1已具备或已具有的可验证可靠性水平(按工程实际通常取0.7置信度可靠性下限值)为0.763 1，明显达不到要求。

为了确保正式飞行任务实施前航天器系统S1应具备0.7置信度下可靠度0.980 0的水平，则在试验飞行任务A和试验飞行任务B共5次飞行任务均成功实施后，根据式(1)～(5)计算得到实施第1次正式飞行任务前航天器系统S1的0.7置信度可靠性下限值0.866 6，点估计值为0.91，如按0.980 0点估计值为目标值来考核，基于当前设计能力是不满足要求的。经计算，基于当前设计验证能力，还需要再成功实施65次飞行任务才能使得航天器系统S1的0.7置信度可靠度下限值达到0.980 0。图4给出了在已知先验数据信息基础上航天器系统S1成功试验次数对其可靠性的影响。可以明显看出：航天器系统S1随成功试验次数增加的可靠性增长趋势。同样，基于表1数据可以得到航天器系统S2和运载火箭系统可靠性随成功飞行试验次数增加的增长趋势。

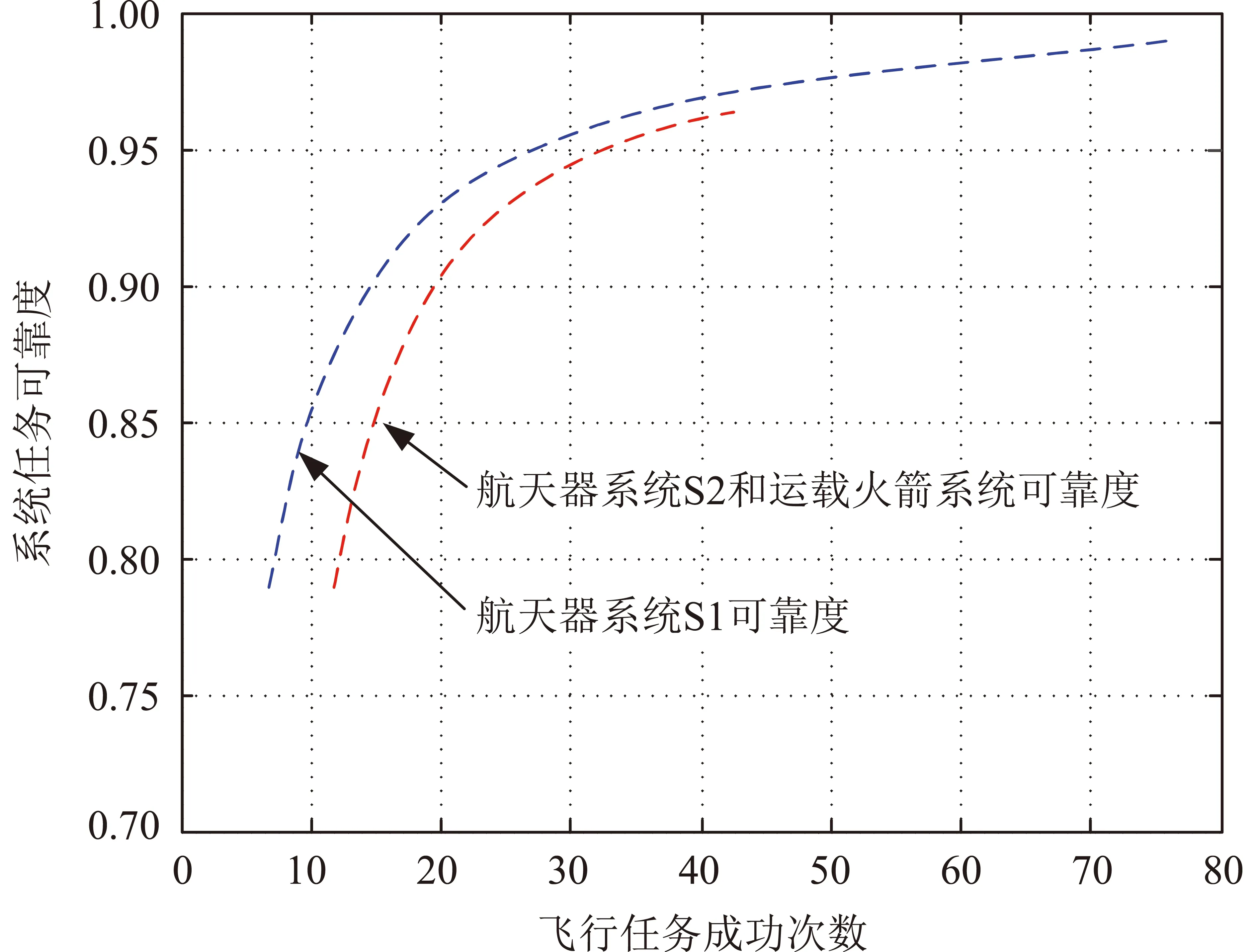
图4 系统任务可靠度随飞行任务成功次数变化趋势(0.7置信度)

这里假设工程规划完成试验飞行任务A成功执行3次，试验飞行任务B成功执行2次的时间周期为3年，飞行任务实施前研制时间为5年，同时假设航天器系统S1通过试验数据累积条件下的可靠性增长能力满足均匀分布模型，且航天器系统S1试验时间在8年周期内等分，则可以将65次飞行试验转换成8年研制周期的可靠性设计及验证能力，则每年等效飞行试验次数为65/8，则5年研制末期首次试验飞行任务A实施前应完成等效飞行试验41次，采用贝叶斯方法计算得到5年研制末期可靠度为0.967 9。假设试验飞行任务A执行3次所需时间为2年，则首次试验飞行任务B实施前等效飞行试验次数为60次，采用贝叶斯方法计算得到首次试验飞行任务B实施前可靠度为0.977 1。假设试验飞行任务B执行2次任务所需时间为1年，则首次正式飞行任务实施前等效飞行试验次数为70次，采用贝叶斯方法计算得到首次正式飞行任务实施前可靠度为0.980 0。根据以上计算结果，可以得到不同阶段的航天器系统S1可靠性指标的门限值和目标值，如表2所示。可以看出：不同阶段的设计要求值0.980 0不变，而首次试验飞行任务A、首次试验飞行任务B及首次正式飞行任务的门限值在不断提高，即设计可验证值随研制任务进展而不断增加。

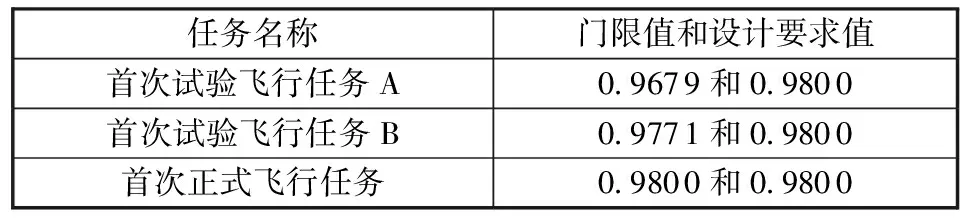
表2 航天器系统S1可靠性指标要求

航天器系统可靠性验证工作可以减少到很短的时间。但是对于新研航天器来说，其影响研制进度及试验规划的因素很多，一些关键产品(如发动机)的设计、试验验证到批生产需要很长周期，甚至一些关键产品生产制造也会耗费大量的时间[14-16]，因此，假设系统通过试验数据累积条件下可靠性增长能力满足均匀分布模型是一种理想情况，在新研产品可利用试验验证能力信息不足的情况下可以近似处理。对于复杂航天产品来说，其相关能力的验证评价需要系统策划和合理有效方法做支撑。

采用同样的方法可以得到航天器系统S2和运载火箭系统的可靠性指标要求，包括门限值和设计要求值。其中：设计要求值是各系统开展研制设计的依据，在实际工程中，通常要保证将来0.7置信度下的系统可靠度0.980 0可验证，系统方案设计时应保证其系统设计的固有可靠度不低于0.990 0，有时设计值甚至会高于设计要求值一个数量级。这样的设计方式存在很大的余量，可以确保在设计、制造、装配及操作等不确定性因素影响下系统的可靠性水平尽可能达到规定的要求。

3 结束语

本文在分析国内外航天工程可靠性指标论证情况的基础上，结合我国航天器研制特点，提出一种新研航天器系统可靠性指标论证方法。以实例形式给出了航天器系统可靠性指标论证过程，介绍了结合研制任务周期、任务实施周期、任务模式及航天器系统历史经验数据等开展各阶段门限值的确定方法，给出了具体的计算流程和公式，实现了从单一设计指标(设计要求值)向阶段验证指标(各阶段门限值)过渡。针对基于数字化研制的新模式下的指标论证新需求，本文方法既适用于新研航天器系统可靠性门限值指标论证工作，也能从可靠性角度为工程整体的任务规划计划提供依据，对其他航天产品的可靠性指标论证工作也有借鉴作用。