考虑夹持效应的滑移式危岩三维稳定性计算方法

邹 鹏，王思奇，罗 刚，赵永杰，李荣发

（1.西南交通大学地球科学与环境工程学院，四川成都 614202；2.四川省国土空间生态修复与地质灾害防治研究院，四川成都 610084）

引言

危岩体是受结构面围限和空间力系作用的三维地质体［1-3］。当危岩体两侧存在夹持作用以及结构面存在锁固段（岩桥）时，传统二维稳定性方法的计算结果存在一定的误差。因此，可采用三维稳定性计算方法以更真实地反应其稳定性状态。

国内外学者就边坡三维稳定性计算方法开展了大量研究。Hovland［4］最早提出运用三维条分法对边坡进行三维稳定性分析。Duncan［5］总结了24篇文献的边坡三维稳定计算方法，并对其计算方法和基本假定进行了详细描述。现有方法可以大概分为以下6种：（1）三维Bishop法［6-8］，满足滑坡条柱Y方向静力和转动力矩平衡；（2）三维Spencer法［9-11］，满足滑坡条柱3个方向静力和转动力矩平衡；（3）三维Janbu法［12-13］，满足滑坡条柱3个方向静力和转动力矩平衡；（4）三维Sarmar法［14-15］，满足所有条块分界面和底滑面均达到剪切极限；（5）三维剩余推力法［16］，满足滑坡条柱3个方向满足静力平衡；（6）严格三维极限平衡法［17-18］，满足滑坡条柱3个方向满足静力平衡。这些计算方法大多是条分法的三维拓展，即条柱法。由于条柱间未知作用力数量较多，为了使问题静定可解，条柱法引入不同的基本假定［9］，这些基本假定由于其不同的特性各有优、缺点［19］。此外，不是所有条柱法都满足6个平衡方程，即便是满足6个平衡方程的严格三维极限平衡法［17］，其稳定性系数的解也并不唯一。对于岩质边坡被多组节理切割的情况，条柱法计算过程十分复杂。因此，条柱法的应用仍存在一定争议。除条柱法外，还存在如概率分析法及数值模型分析等方法［20-22］，但这些方法均存在其不同的优缺点，且需进行复杂的计算。

文中基于空间解析几何学和极限平衡法，同时可考虑各结构面上所有力对危岩体的影响，提出了一种可考虑周围岩体夹持作用的滑移式危岩三维稳定性计算方法，为危岩体稳定性评价提供科学的计算方法。

1 计算模型及理论推导

1.1 规范方法

滑移式危岩体是一种常见的地质灾害，我国规范中一般采用将三维问题简化为二维问题的方式计算其稳定性。而对于楔形体滑块《YS/T 5230-2019边坡工程勘查规范》规定：对于岩质边坡被多组节理切割的情况，块体稳定性应根据破坏的边界条件，按空间问题进行分析［23］。比如，由两组结构面切割形成潜在滑移楔形体（图1），其可能沿结构面交线下滑，边坡稳定系数按下式计算：

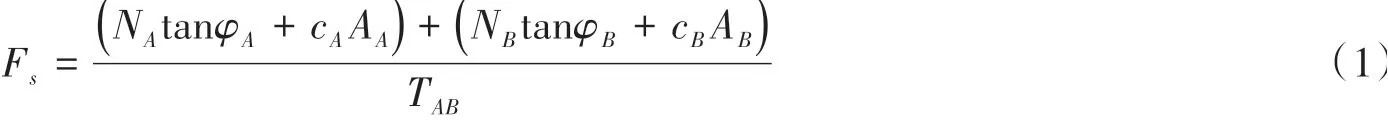
式中：NA、NB为潜在滑移体所受重力作用于A、B结构面上的法向分力（kN）；TAB为潜在滑移体所受重力在组合交线上的切向分力（kN）；TA、TB为A、B结构面的面积（m2）；cA、cB为A、B构面的黏聚力（kPa）；φA、φB为A、B结构面上的内摩擦角（°）。

楔形体稳定性计算方法由于其计算过程简单而得到了广泛的应用。但由于其只能计算天然和地震工况，无法计算降雨工况下楔形体的稳定性系数，所以该方法具有一定局限性。

当岩质边坡为斜向坡时（即底滑面倾向与坡面倾向斜交），危岩体存在视倾向滑动可能［22］，危岩体将受到两侧岩体夹持作用。此外，背斜核部和逆冲断层带处的危岩体也可能受到两侧岩体夹持作用。根据危岩体空间几何形状，危岩体可分为3种情况：上大下小模型（图2（a））、上小下大模型（图2（b））和上下等大模型（图2（c））。文中主要介绍上大下小模型的具体计算过程，其余两种类型可根据该过程依次类推。

图1 由两组结构面切割形成潜在滑移楔形体Fig.1 Potential sliding block controlled by two sets of structural planes

图2 危岩体模型Fig.2 Models of unstable rock mass

1.2 危岩体几何模型

如图3所示上大下小模型危岩体，假定危岩体受3组结构面切割而成，危岩体底部缓倾结构面倾角为θ，两侧陡倾结构面倾角为β1和β2。锁固段（岩桥）由面BCPGF构成，裂隙面由面ABFE、面ABCD和面EFGH构成。面ADHE平行于面BCPGF并与水平面成θ角；线段AE、CG、DH和BF均平行于水平面；过BF中点O作垂线交CG于P点。对各结构面建立局部坐标系（表1）。

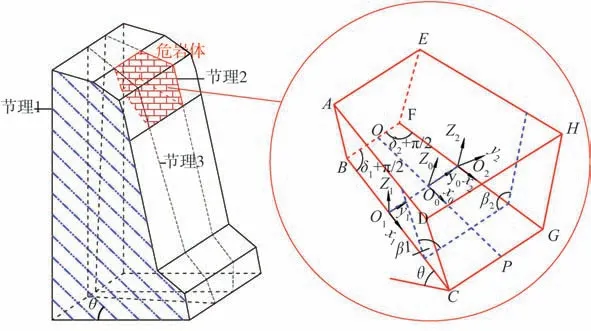
图3 滑移式危岩体三维几何模型Fig.3 Three-dimensional geometric model of unstable rock mass with a sliding plane

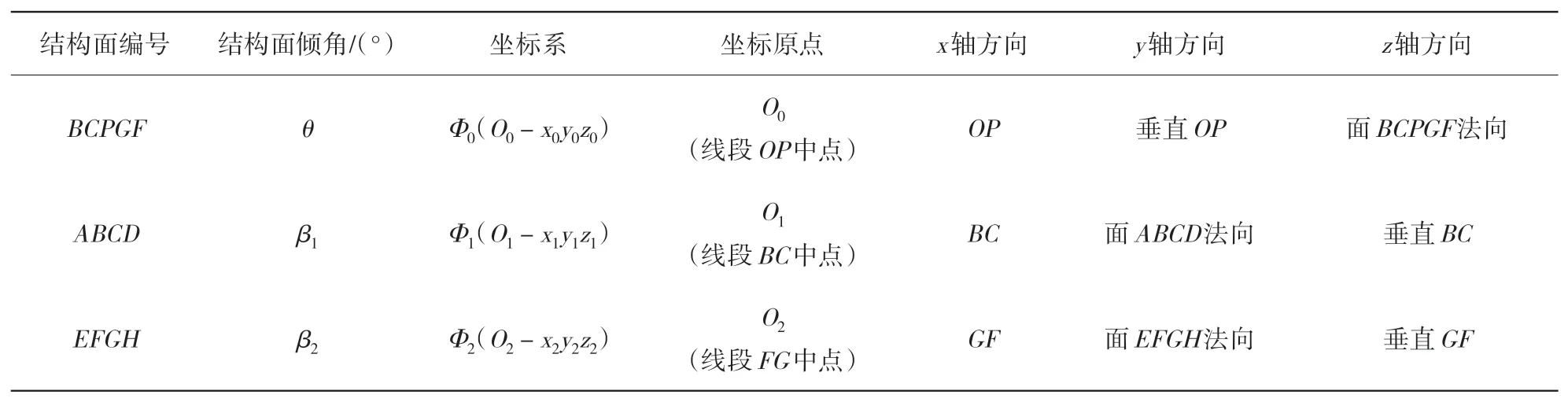
表1 结构面空间几何形态参数Table 1 Spatial geometry parameters of structural planes

1.3 基本假定

考虑危岩体最不利条件，该模型的基本假设有：

（1）锁固段岩石抗剪强度取岩石峰值粘聚力cf和峰值内摩擦角φf，裂隙面抗剪强度取岩石残余内摩擦角φr；

（2）面BCPGF、面EFGH、面ABCD、面ABFE均达到极限平衡状态，满足Mohr-Coulomb准则；

（3）由于两侧夹持效应，忽略侧面和底面的转动作用，危岩体只沿底滑面的合力方向滑动；

（4）假定结构面ABCD所受力的作用点为AB边和BC边中垂线的交点，结构面EFGH所受力的作用点为FE边和FG边中垂线的交点。

1.4 空间向量的等效变换

空间向量的等效变换可以看作是坐标系之间的变换，即将坐标系Φ1、Φ2先进行转轴变换再进行移轴变换。该过程中所求得公式即为空间向量的变换公式。

（1）空间坐标系的转轴变换

为了将坐标系Φ1中的向量变换至坐标系Φ0，需要补充2个辅助坐标系Φ11和Φ12（图4）。坐标系Φ11（O1-x11y11z11）为坐标系Φ1绕x1轴顺时针旋转β1-π/2角度得到的坐标系（图4（a）），坐标系Φ12（O1-x12y12z12）为坐标系Φ11绕z11轴逆时针旋转δ1角度得到的坐标系（图4（b））。坐标系Φ1和坐标系Φ11各坐标轴夹角，如表2所示，坐标系Φ11和坐标系Φ12中各坐标轴夹角，如表3所示。

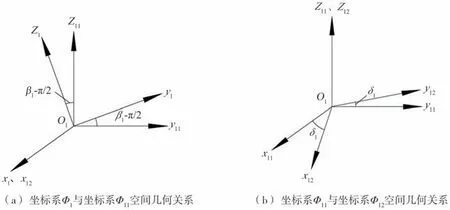
图4 坐标系Φ1、Φ11和Φ12空间几何关系Fig.4 Spatial geometric relationship among the coordinate systems Φ1，Φ11 and Φ12

表2 坐标系Φ1坐标轴与坐标系Φ11坐标轴夹角Table 2 Angles between coordinate systems Φ1 and Φ11

表3 坐标系Φ11坐标轴与坐标系Φ12坐标轴夹角Table 3 Angles between coordinate systems Φ11 and Φ12

由表2可得从坐标系Φ1旋转至坐标系Φ11的旋转矩阵为：

由表3可得从坐标系Φ11旋转至坐标系Φ12的旋转矩阵为：

所以将坐标系Φ1中向量旋转至与坐标系Φ0的旋转矩阵为：

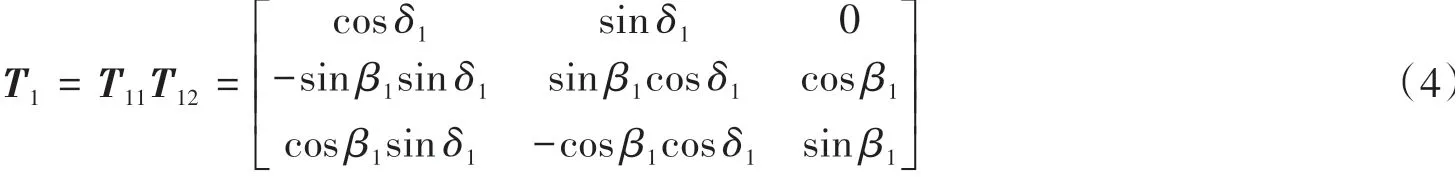
同理可得，将坐标系Φ2中向量旋转至与坐标系Φ0坐标轴的旋转矩阵为：

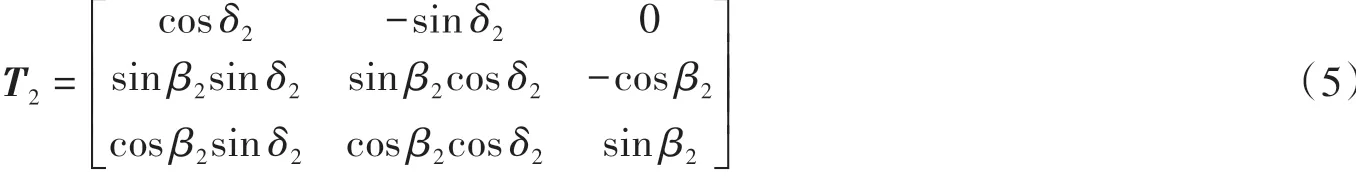
（2）空间坐标系的移轴变换

根据空间解析几何，空间坐标系的移轴变换公式为：

式中：x、y、z为旧坐标系中坐标值；x′、y′、z′为新坐标系中坐标值；x0、y0、z0为新坐标系坐标原点在旧坐标系中的坐标值。

根据移轴式（6）求得O0点在坐标系Φ12和坐标系Φ22中的坐标值以及平移向量（表4）。

（3）空间向量的变换公式

由式（5）和式（6）可推导出空间向量的变换公式为：

表4 O0在坐标系Φ12和Φ22中坐标及平移向量Table 4 Coordinates of point O0 in coordinate systems Φ12 and Φ22 and translation vectors

1.5 天然工况下危岩体稳定性计算

天然工况下，只考虑重力作用，对危岩体进行切割，将重力分配到各结构面对应的局部坐标系Φ1和Φ2，进行受力分析并用空间向量表示（图3），再将所有空间向量变换至主滑面坐标系Φ0。基于Mohr-Coulomb准则，计算主滑面上的抗滑力和下滑力，求出稳定性系数Fs。具体计算过程如下：

（1）计算坐标系Φ0（O0-x0y0z0）中所受的力

多面体ABCDEFGH的重力W0在坐标系Φ0中向量为W′0；

结构面ABFE的抗滑力F0，其大小为：

式中：NABFE为潜在滑动体重力在结构面ABFE法向的分量；φ0为结构面ABFE的内摩擦角；c0为结构面ABFE的内聚力；A0为结构面ABFE的面积。

其在坐标系Φ0中向量为F′0。

（2）计算坐标系Φ1（O1-x1y1z1）中所受的力

结构面ABCD的抗滑力F1，其大小为：

式中：NABCD为潜在滑动体重力在结构面ABCD法向的分量；φ1为结构面ABCD的内摩擦角；c1为结构面ABCD的内聚力；A1为结构面ABCD的面积。

其在坐标系Φ1中向量为

式中：a、b为结构面ABCD的力作用点的坐标。

将空间向量F1变换至坐标系Φ0：

（3）计算坐标系Φ（2O2-x2y2z2）中所受的力

同上可得，将结构面EFHG的抗滑力F2变换至坐标系Φ0的变换公式为：

（4）空间滑移式危岩体稳定性计算

x0轴方向合力Fx0为：

y0轴方向合力Fy0为：

下滑力T为：

抗滑力R为：

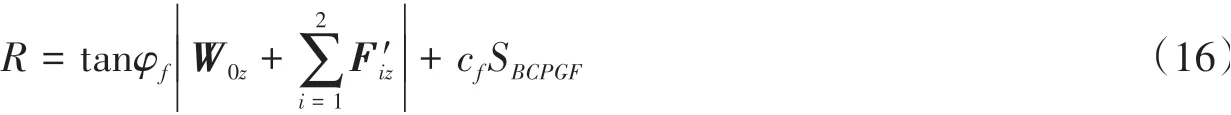
稳定性系数Fs为：

滑动方向与x0轴夹角δ为：

1.6 暴雨工况下危岩体的稳定性计算

暴雨工况下，考虑最危险情况（后侧与两侧结构面全部被水充满），结构面抗剪能力完全丧失，只剩下静水压力作用。岩体的重度取饱和重度，重力的计算过程与1.5节相同。静水压力具体计算过程如下：

（1）坐标系Φ0（O0-x0y0z0）中所受的静水压力

结构面ABFE上静水压力Fw0在坐标系Φ0中的向量为F′w0。

（2）坐标系Φ1（O1-x1y1z1）中所受的静水压力

结构面ABCD上的静水压力Fw1在坐标系Φ1中向量为Fw1。

将空间向量Fw1变换至坐标系Φ0：

（3）坐标系Φ2（O2-x2y2z2）中所受的静水压力

结构面EFGH上的水压力Fw2在坐标系Φ2中向量为Fw2。

将空间向量Fw2变换至坐标系Φ0：

（4）空间滑移式危岩体稳定性计算

x0轴方向Fx0合力为：

y0轴方向Fy0合力为：

下滑力T为：

抗滑力R为：

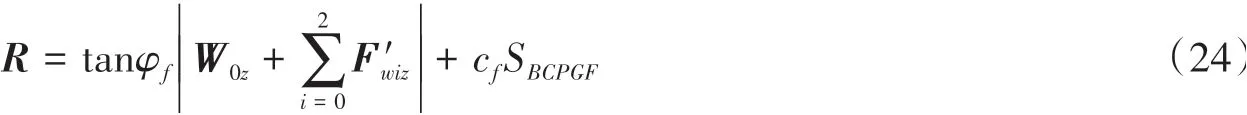
稳定性系数Fs与滑动偏转角δ同1.5节。

1.7 地震工况下危岩体的稳定性计算

地震工况下，考虑竖向和水平向的地震惯性力。计算过程与1.5节相同。根据《建筑抗震设计规范（GB 50011-2010）》［24］，地震惯性力计算公式如下：

地震水平惯性力Fhi：

地震竖直惯性力Fvi：

式中：a1为水平地震影响系数值，按表5取值；avmax为竖向地震影响系数的最大值，取水平地震影响系数最大值的65%；Geq为总重力荷载。

表5 水平地震影响系数最大值Table 5 The maximum value of horizontal seismic influence coefficient

（1）坐标系Φ0（O0-x0y0z0）中所受的力

由于水平和竖向地震惯性力的作用，潜在滑动体的重力应减去竖向地震力部分，则：

水平惯性力Fh0=a1GABCDEFGH，在坐标系Φ0中向量为Fh0。

（2）坐标系Φ1（O1-x1y1z1）中所受的力

由于竖向地震惯性力的作用，该坐标系内的抗滑力F1=NABCDtanφ1+c1A1，其在坐标系Φ1中向量为F1。

将空间向量F1变换至坐标系Φ0：

（3）坐标系Φ2（O2-x2y2z2）中所受的力

该坐标系内计算方法同坐标系Φ1，可得到坐标系Φ0内空间向量F2′。

（4）空间滑移式危岩体稳定性计算

x0轴方向合力Fx0为：

y0轴方向合力Fy0为：

下滑力T为：

抗滑力R为：

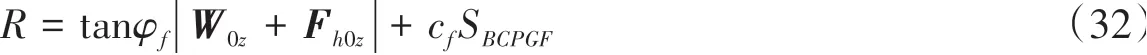
稳定性系数Fs与滑动偏转角δ同1.5节。

2 算例

陈祖煜等［9］曾在其发表文章中对楔形体问题进行计算，其算例考察一个如图5所示的楔形体，其几何形体和物理参数如表6所示，其中楔形体坡高64.89 m，岩石容重26 kN/m3。计算左、右结构面强度参数相同和不同2种工况。

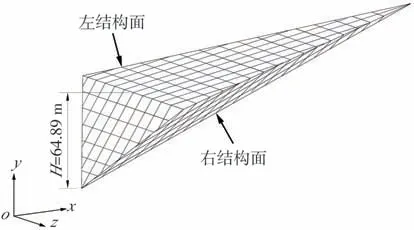
图5 楔形体稳定性分析算例Fig.5 A stability analysis example of wedge sliding body

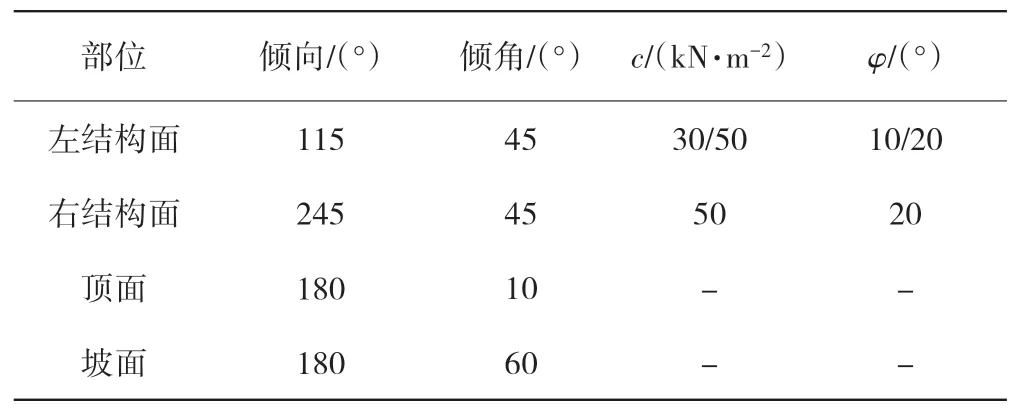
表6 楔形体的几何、物理参数Table 6 Parameters of geometry and geotechnical properties of wedge sliding body

当两侧结构面参数一致时，陈祖煜算法和规范算法算出的安全系数均为F=1.55，文中算法得出的安全系数为1.52。当两侧结构面参数不一致时，陈祖煜算法和规范算法算出的安全系数均为F=1.18，文中算法得出的安全系数为1.16。由此可见，对于给出的算例，文中计算方法的结果与规范算法和陈祖煜算法较为接近，证明文中算法的有效性和合理性。

3 结论

（1）针对滑移式危岩体，采用空间解析几何和极限平衡法，提出了一种可考虑危岩体两侧夹持效应的危岩三维稳定性计算方法。首先对危岩体围限的结构面建立各自的坐标系，计算各坐标系的空间力系，通过矢量变换，求得主滑面的抗滑力和下滑力，最终得到危岩体整体稳定性系数。相较于二维方法，更加符合危岩体实际受力条件。

（2）危岩体两侧夹持作用和岩桥（锁固段）抗剪作用对危岩体稳定性有利。通常，当区域最大主应力与边坡走向一致，且岩体结构面紧闭（张开度很小），可考虑侧面的夹持效应。当结构面不连续，存在岩桥时，可对结构面进行强度参数分区设置。

（3）经典的楔形体（危岩）稳定计算方法，假设危岩体沿交线方向滑动。首先将重力分解为垂直交线和平行交线的分量，然后将垂直分量投影至两个滑动面的法线方向。其实质即为：将滑动体自重分别分配到两个滑动面。文中提出方法经退化后与该计算方法一致，可认为是本方法的一种特例。