雨水管网模型子汇水区划分与模拟精度
2022-11-15杨佳利徐拥军梁藉唐颖刘子龙
杨佳利,徐拥军,梁藉,唐颖,刘子龙
(1.华中科技大学土木与水利工程学院,武汉 4730074;2.中国电建华东勘测设计研究院有限公司 东南区域总部,杭州 311100;3.北京城市学院城市建设学部,北京 100083;4.北京城市规划设计研究院,北京 100045)
目前,随着国内城市化进程加快,道路硬化建设致使地表不透水面积增大,加之极端暴雨事件频发,城市内涝灾害激增[1-2]。内涝分析是解决城市积水问题的基础手段,高精度城市雨水管网模型是分析城市内涝的必要前提[3]。城市雨水管网模型利用城市降雨、地形、管线工程等基础数据,模拟城市产汇流过程,分析城市管网排水能力及地表淹没状况。在水文模型中,子汇水区划分通过影响管网节点处的雨水入流过程和管道内的雨水汇流过程,引起模型管段出水口流量峰值、峰现时间等重要模型精度评价指标变化,子汇水区划分合理性是管网模型与实测拟合程度的决定性因素之一[4]。因此,要提高城市雨水管网模型精度,就需要合理划分子汇水区。
对于子汇水区划分方法,国内外已有大量相关研究[5-18],但主要针对山区、流域水文模型的子流域汇水区划分。Rouhani等[10]结合Shuffled Complex Evolution(SCE)优化算法,制定多自动校准方案(MACS)划分流域子汇水区,研究了不同降雨空间分布情景下子汇水区划分对径流预测的影响。Lei等[11]提出了一种适用于区域尺度的流域汇水区划分方法,成功应用于中国南水北调中线工程。Choi等[12]开发了一种基于Web的实时流域地理信息系统,利用双种子数组替换算法(double-seed array-replacement algorithm)从点坐标获得分水岭边界,并利用印第安纳州的Wildcat Creek流域数据进行了模拟,其精度较高。Luo等[13]改进ArcGIS和ArcSWAT默认DEM的预定义流域划定方法,创新一种基于DEM和DCN划定河流子流域方法,子流域划分结果与圩田地区的实际水文过程吻合较好。Liao等[14]提出了一种基于六边形网格空间离散化流域划分方法,据此构建模型,分别应用于美国西部陡峭和平坦两种地形情景的分水岭划分,结果比传统空间离散方法在重现流域轮廓方面更具优势。Lai等[15]提出了一种基于水文特征和DEM的流域划分方法,依据矢量水文特征数据模型提取河流节点,根据水流方向矩阵和河流节点的位置完成流域划分,并应用于构建中国西部太湖流域水文模型,与传统方法相比,它可同时考虑不同类型流域和多个入口出口的情景,有利于PRNR分布式水文模型的开发。Castronova等[16]使用数学图论来识别流域边界,提出了基于层次网络的开源划定方法,与传统仅从数字高程模型导出流域栅格算法相比表现出更大的灵活性、可扩展性,并有效提高了模型精度。
然而,针对城市子汇水区划分方法的研究略少[19-29]。1911年荷兰气候学家A.H.Thiessen提出了一种依据离散分布的降雨气象站位置划分汇水区的方法——泰森多边形法[19]。泰森多边形法广泛运用于城市子汇水区划分,一般采用管网节点或者出水口作为泰森多边形法划分子汇水区据点。李若男等[20]依据泰森多边形法构建上海黄浦区北部区域的ICM水动力模型,较好地模拟了不同重现期降雨情景下的一维地表洪水过程及地表淹没深度和二维地形条件下的城市内涝积水深度及流速,为该城市制定防洪排涝方案提供了理论依据。然而泰森多边形法划分子汇水区未考虑地形因素的局限性,导致汇水区等距均分,划分结果与实际汇水区存在一定的偏差,且易出现汇水边界切割建筑物等不符合实际地表汇流的情况,不确定性显著[21-22]。Warsta等[23]使用统一的计算网格划分研究区域子汇水区,为城市雨水管网模型SWMM开发了一个子汇水区生成程序。Wu等[24]提出了一种基于坡度和坡向的精细化划分SWMM模型子汇水区的新方法,该方法准确设置模型参数和水力交换条件,在一定程度上提高了模型的精度,但该方法对坡度数据精度要求高,不适用大面积城市区域管网建模。Back等[25]提出了一种基于GIS的自动划分城市子流域方法,该方法考虑了自然地表倾角,将实际的管网节点与雨水箅共同作为节点,以此作为子汇水区出口,分别使用数字表面模型(DSM)和数字高程模型(DEM)自动划分城市子汇水区,并将SWMM的水力模拟结果与实测流量数据进行比较。Ji等[26]提出了一种新的SWMM子汇水区划分方法,该方法依据城市子汇水区地形和水文信息的空间变异性特征,利用流域分区方法从DEM中提取道路和管网,并在划分方法中引入GIS技术,基于空间分析方法根据道路、管道和建筑物的分布特征调整原始DEM数据,从而进一步提高SWMM的模拟结果。Döring等[27]提出了从土地利用数据计算子集水区面积和从街道地形计算雨水排水网络的算法,以区域尺度的SWMM排水管网模型为研究对象,建立了测试案例,在小型测试区域中所提出算法表现良好,但由于不透水地表覆盖百分比推导方面不完善,无法适用于大型研究区域。Li等[28]提出了一种兼顾土地利用类型和流向的子汇水区划分方法,将研究区划分为一级汇水区和二级汇水区(FL和SL),并利用修正的DEM(数字高程模型)和流向数据,将SL汇水区划分为三级基于方向的(D-B)汇水区,提出了一种基于土地利用的D-B子汇水区划分算法,并在新算法中引入自适应阈值调整,该方法适用于大城市。Bai 等[29]研究利用无人机传感器来检查地形和土地使用覆盖变化,通过测量数字地表模型和正射影像图,获得城市子汇水区,利用最小累积阻力模型模拟了166个城市子汇水区径流,得到了多条连接城市上下水系的径流路径,地表径流分配与实际匹配度高。
以上研究中,泰森多边形法划分子汇水区未能考虑地形因素,且山区流域水文模型子汇水区划分无法直接用于管网模型中的子汇水区划分。因此,本文提出一种基于盆域分析的泰森多边形子汇水区划分方法(basin analysis based Thiessen polygon subcatchment division method,BATP),通过此方法将地形因素和管网系统综合考虑。同时以北京某区域为例,将BATP方法分别与人工绘制法、传统泰森多边形法进行对比,以井下液位峰值、峰现时间及流量峰值、峰现时间、总流量等模拟结果为依据验证方法,评估BATP方法的优势。
1 基于盆域分析的泰森多边形子汇水区划分方法
只有子汇水区地表径流通过唯一管网节点汇入管段,才能满足雨水管网模型构建要求。子汇水区划分通过界定汇水范围影响管网节点处的雨水入流过程以及管道内的雨水汇流过程,进而改变模型管段出水口流量峰值、峰现时间等精度评价指标数据,所以划定子汇水区范围并确定合理的管网入流节点会对管网模型的精确度产生较大影响。城市子汇水区划分主要考虑两大问题:城市下垫面类型多且不同用地类型分布零散,地形因素对子汇水区划分影响较大;城市管网密布且错综复杂,汇水范围难以界定。因此,提出BATP方法,以地形为基础合理划分子汇水区。首先依据城市地形数据进行盆域分析,划分出汇流范围集中的径流单元,将该径流单元定义为初级子汇水区;其次修定初级子汇水区,对不存在管网节点的初级子汇水区,寻求周围公共边界高程最小值对应的初级子汇水区与之合并,以保证每个初级子汇水区内均存在管网节点;最后采用泰森多边形法细分初级子汇水区,得到与管网节点一一对应的子汇水区。由此准确模拟子汇水区内径流顺自然地表流入管网节点、按城市水文路径输入雨水管道系统至出水口排出的全过程,从而提高模型精度。
1.1 划分初级子汇水区
使用高分辨率的数字高程模型栅格数据进行盆域分析,划分得到汇流集中且高程变幅小的初级子汇水区。初级子汇水区划分过程见图1,具体步骤如下:

图1 初级子汇水区划分
地形填洼处理[30]:避免人为因素导致的地形误差而形成不合理水流方向的情况发生,需对错误的低洼点进行填洼处理。
流向分析:根据每个DEM栅格的最陡坡度方向,运用D8流向原理连通各像元流向栅格,完成区域的流向分析。
流量分析:基于流向分析后,统计每个像元栅格的累计汇流流量值。
地表径流分级处理:基于汇流累积量数据设定阈值生成城市栅格径流网络,提取地表径流分布。
地表径流网矢量化:将分级后的边界栅格网络转换为线状边界,准确界定地表径流范围,划定地表径流网络边界线。
生成盆域:依据流量、流向、径流网确定栅格的上游汇流区域,将城市地表划分为若干盆域,即初级子汇水区。
1.2 初级子汇水区的修定
盆域分析是直接的地形分析方法,未考虑城市管网分布,所以划分得到的初级子汇水区未必均存在管网节点,不存在管网节点的子汇水区无法满足雨水管网模型建设需求,因而对不存在管网节点的初级汇水区采用就近合并方法。选择与该初级汇水区最邻近且公共边界高程最小的一个初级子汇水区,合并生成一个新初级子汇水区。依据地形DEM数据,找出不存在管网节点初级子汇水区周围公共边界高程最小的初级子汇水区即其下方子汇水区,两者合并成为一个新初级子汇水区,见图2。
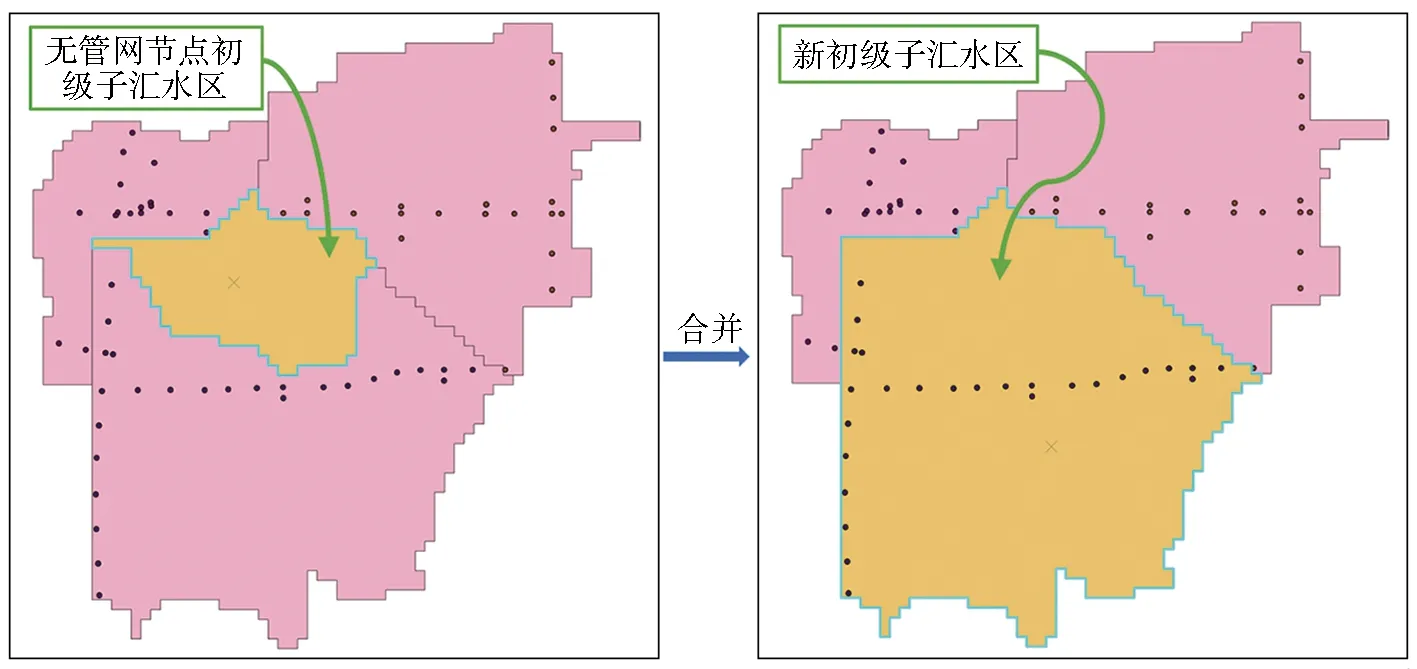
图2 初级子汇水区修正
1.3 子汇水区的确定
修定后的初级子汇水区存在一个或多个管网节点,仅存在唯一管网节点的初级子汇水区即为该管网节点的子汇水区。存在多个管网节点的初级子汇水区,需进一步采用泰森多边形法细化管网节点汇水范围,界定与管网节点一一对应的子汇水区。以管网节点为据点采用泰森多边形法划分得到子汇水区,见图3。

图3 初级子汇水区生成子汇水区
BATP划分方法全过程见图 4,最终得到与城市管网节点唯一匹配的子汇水区。

图4 BATP划分方法流程
2 研究实例
2.1 实例概况
选择北京市某区域作为研究实例,研究区域面积4.244 58 km2,不透水地表面积占比为72.534%,用地类型主要包含道路、房屋、硬化铺装、植被和裸土。研究区域覆盖907条主干管,管段总长29.687 km,最长管131.8 m;存在902个管网节点、1个雨量计及1个出水口。采用分辨率为10 m×10 m的数字高程模型栅格数据。研究区域用地类型、高程及管网布局见图 5。

图5 研究区用地类型、高程及管网布局
2.2 研究区模型构建与参数率定
子汇水区划分完成后,才能建立雨水管网模型进行参数率定。为了得到一组客观的汇水区产汇流参数,并在后续评价中较为真实地对比不同子汇水区划分方法对于雨水管网模型精度的影响,需先拟定一种子汇水区划分方法建模率定参数。人工绘制法划分子汇水区是专业人员依据DEM高程栅格数据、卫星影像图和研究区不同用地类型数据,精细化地物高程数据后,手动勾画每个管网节点对应子汇水区的方法。该方法的划分工作过程繁琐、工作量大,但能准确吻合实际管网节点所服务的汇水区范围。因此,以人工绘制法划分子汇水区进行参数率定,统一汇水区参数设置。采用人工绘制法划分汇水区构建雨水管网SWMM模型见图 6、图 7。

图6 人工绘制法划分研究区域汇水区

图7 人工绘制法构建的SWMM管网模型
模型率定选取2020年汛期实测数据:采用实测降雨(一)率定参数,该降雨历时20.5 h,总降雨量342 mm;采用实测降雨(二)验证参数率定结果,该降雨历时20.5 h,总降雨量551 mm。监测点位于该研究区域出水口的上游管渠,监测指标包括液位和流速数据,实测雨量、液位及流量数据见图 8、图 9。

图8 实测降雨(一)及其对应液位、流量曲线

图9 实测降雨(二)及其对应液位、流量曲线
《城市内涝防治系统数学模型构建和应用规程》[31]中模型率定的相关要求:模拟及实测峰值流量和液位时间偏差均应小于 1 h;峰值流量和峰值液位数值偏差不应大于25%;模拟和实测的总流量偏差不应大于20%。采用率定参数建模获得的各项指标数据与实测数据对比见表1,实测降雨(一)流量及液位峰现时间与实测峰现时间间隔仅差距2 min,拟合效果好;管道流量、液位峰值偏差分别为17.044%、6.981%,总水量偏差为17.000%,均满足《城市内涝防治系统数学模型构建和应用规程》对于模型率定的相关要求,率定结果见图 10、图 11。综上所述,采用此次率定的参数构建模型精度较好,最终确定的不同产汇流表面降雨径流模型参数,见表 2。将参数率定结果用于构建实测降雨(二)管网模型,结果显示:流量及液位峰现时间与实测峰现时间间隔仅差距1 min;管道流量、液位峰值偏差分别为3.708%、8.039%,总流量偏差为16.650%,各项管网指标与实测值偏差较小,满足规范要求,结果见图 12、图 13。因此,此次模型参数率定取值合理,适用性较好。

表1 参数率定模型结果与实测对比

图10 实测降雨(一)监测点模型流量率定结果

图11 实测降雨(一)监测点模型液位率定结果

表2 汇水区降雨径流模型参数率定值

图12 实测降雨(二)监测点模型流量率定结果

图13 实测降雨(二)监测点模型液位率定结果
2.3 子汇水区划分
利用研究区域管网节点、管段、出水口、雨量计相关基础数据,运用BATP方法划分子汇水区,得到基于盆域分析获得的初级子汇水区和最终划分的子汇水区结果见图 14、图 15。为验证BATP方法划分子汇水区优越性,选取人工绘制法和传统泰森多边形法与其进行对比。传统泰森多边形法划分子汇水区快速简便,操作易行。人工绘制法划分子汇水区与实际管网节点所服务的汇水区范围拟合度高。以人工绘制法模型结果作为参照,分别比较BATP方法、泰森多边形法划分子汇水区模型结果差异,从而评估3种方法对模型精度的影响。传统泰森多边形法划分结果见图 16。人工绘制法构建的管网模型见图 7。
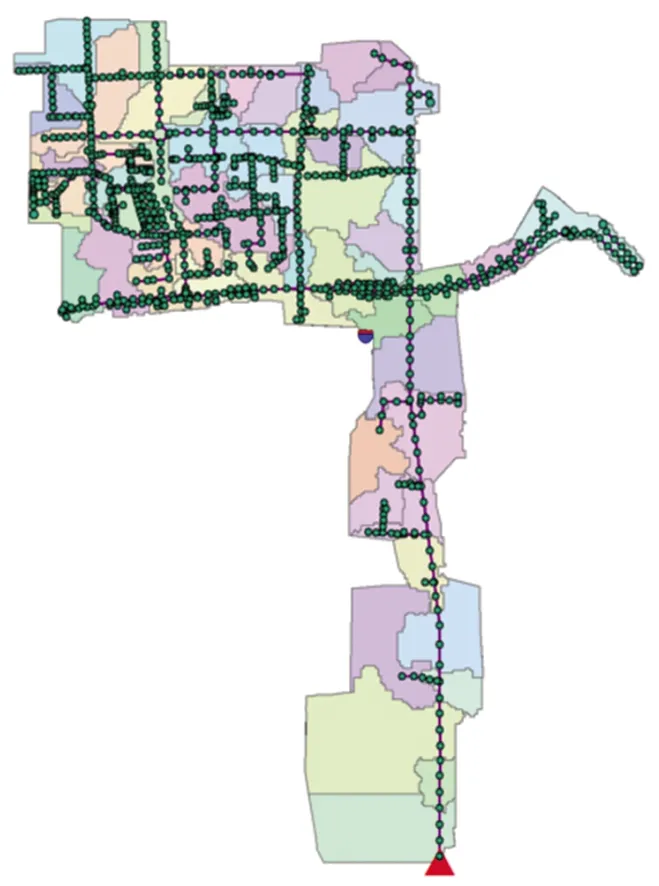
图14 基于盆域分析划分的初级子汇水区

图15 最终划分的子汇水区

图16 泰森多边形方法划分的子汇水区
3 模拟结果比较
在实测降雨(一)和设计降雨两种情景下,分别运用BATP方法、人工绘制法和泰森多边形法构建雨水管网模型,对比模拟结果并分析指标差异。
3.1 实测降雨模拟对比
将图 8实测降雨(一)数据分别导入依据3种子汇水区划分方法构建的管网模型,比较模拟结果。监测点模型与实测液位、流量曲线分别见图 17、图 18。3种方法模型评估指标对比见表 3。计算结果表明:BATP方法、人工绘制法和泰森多边形法模拟的液位流量峰现时间间隔分别为3、2、7 min,均满足小于1 h的标准;模型液位峰值偏差分别为1.115%、6.981%、17.059%,流量峰值偏差为1.301%、17.044%、23.330%,均满足不大于25%的标准;模型总流量偏差分别为6.796%、17.000%、40.343%,仅泰森多边形法模型结果不满足20%的标准[31]。综上可见:BATP方法、人工绘制法模型与实测拟合度好,模型精度高;泰森多边形法模型与实测拟合不佳,模型精度低。

图17 实测与模型液位对比曲线

图18 实测与模型流量对比曲线

表3 3种方法模型指标对比
3.2 设计降雨情景下方法差异度分析
为进一步对比BATP方法、人工绘制法和泰森多边形法的差异,将3种方法运用于设计降雨情景进行模拟,采用成对比较检验法来分析实测数据与模型结果相似程度。设计降雨采用北京市重现期为1、2、3、5、10、20、30、50、100 a的9种芝加哥雨型,见图 19。

图19 设计降雨雨型
出水口液位及流量由汇水区范围及面积决定,按重现期顺序分别绘制出水口流量随时间的变化过程线。降雨重现期不断增大时,出水口液位及流量峰值增幅均上升。为了便于比较,表 4、表 5分别列出了不同重现期下3种方法模拟的出水口液位及流量峰值。人工绘制法是人工依据实况划分的,因而汇水区范围划定较准确。以人工绘制法模型出水口流量过程线为参照曲线,运用成对比较检验法,对3种方法划分子汇水区得到的出水口液位及流量峰值分别进行成对样本检验,检验结果见表 6、表 7。

表4 在不同重现期下3种方法模拟的液位峰值

表5 在不同重现期下3种方法模拟的流量峰值

表6 出水口液位峰值不同方法成对样本检验

表7 出水口流量峰值不同方法成对样本检验
采用成对样本检验的数学分析方法,求出3种方法两两对比的Sig值,进而评估指标显著性差异。Sig计算公式为
式中:n为自由度;Γ(n)为伽马函数;χ2(n)为卡方分布函数。
数学分析中,以Sig0=0.05作为显著性临界值。由表 6、表 7可以得出:BATP方法与人工绘制法液位及流量成对样本检验的Sig 分别为0.288和0.068,均大于Sig0,未达到显著性水平;而泰森多边形法与人工绘制法液位及流量成对样本检验的Sig 均为 0,远小于 Sig0,在显著性范围内。综上所述,泰森多边形法未考虑地形因素,SWMM模型精度低,而BATP方法较泰森多边形法在划分子汇水区时加入了地形盆域分析,汇水区范围划定结果更接近人工实况汇水区,所以模拟结果更准确,模型精度高。
计算得出,泰森多边形法、BATP方法与人工绘制法的液位及流量峰值偏差,分析结果(表 8、表 9)显示,各重现期下泰森多边形法与人工绘制法液位及流量峰值偏差均为负值。以±3%为偏差指标,所有设计降雨情景下,泰森多边形法的模型液位及流量峰值偏差率均小于-3%,BATP方法与人工绘制法液位及流量峰值偏差均在±3%范围内。因此,泰森多边形法构建的雨水管网模型结果液位峰值、流量峰值均偏低,模型精度不佳。

表8 泰森多边形法液位偏差分析
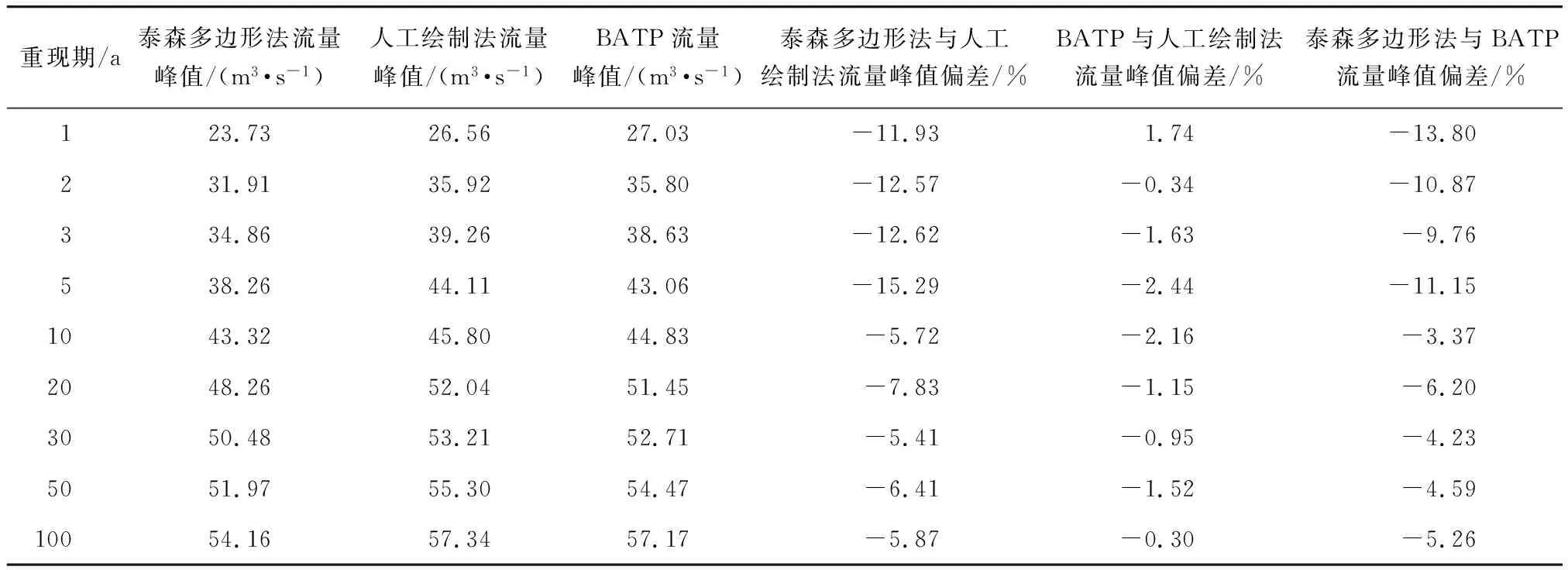
表9 泰森多边形法流量偏差分析
4 结 论
人工绘制法划分子汇水区的模拟结果与实测数据偏差较小,满足规范要求,精度较高。
BATP方法划分子汇水区的模拟结果与人工绘制法模拟结果较为接近,且与实测值偏差小,模型精度较高。
泰森多边形法由于缺少地形因素考虑,划分的子汇水区得到的模型结果与实测值均偏差较大。因此,考虑地形因素可有效提高雨水管网模型精度。
人工绘制法对绘制人员的专业程度要求较高,且划分过程繁琐复杂,而BATP方法可结合计算机技术自动划分子汇水区,操作简单,节省时间和精力,并可以获得较高精度的模型结果。
