含中间质量改进三参数隔振器动力学特性研究
2022-11-14朱冬梅肖凯莉刘海平
朱冬梅 肖凯莉 刘海平


摘要:通過在含X形机构非线性三参数隔振器中引入中间质量,提出一种改进三参数隔振器并建立其理论模型.采用谐波平衡法得到隔振系统的稳态解析解,利用四阶龙格库塔法和多体动力学软件ADAMS验证其正确性.将力传递率作为评价隔振系统动态性能的技术指标,与传统三参数隔振器以及含X形机构非线性三参数隔振器进行对比,结合工程实际,分别给出3种类型隔振器在多频稳态激励下的时域位移响应,并进行对比研究.分析了该隔振系统的功率流特性以及能量特征,选择隔振系统部分关键设计参数进行影响因素分析.从动力吸振器的角度,讨论了所提模型中非线性连接方式对其减隔振效果的影响.计算结果表明,合理选择中间质量可以在原隔振系统谐振频率附近形成一个反共振低谷,且系统固有频率向低频移动,使隔振系统有效隔振频带变宽;相比于传统三参数隔振器和含X形机构非线性隔振器,隔振系统在低频和高频的隔振性能均得到有效提升;通过力传递率评估设计参数,结果表明各参数均存在最优值;将线性动力吸振器与接地X形机构连接,可进一步改善其减隔振效果.
关键词:非线性分析;隔振器;谐波平衡法;中间质量;动力学分析
中图分类号:TB123文献标志码:A
Research on Dynamics Characteristics of Improved Three-parameter Isolator with Intermediate Mass
ZHU Dongmei,XIAO Kaili,LIU Haiping
(School of Mechanical Engineering,University of Science and Technology Beijing,Beijing 100083,China)
Abstract:By introducing an intermediate-mass into the nonlinear three-parameter isolator with an X-shaped mechanism,an improved three-parameter isolator is proposed,and its theoretical model is established. The Harmonic Balance Method is used to obtain the steady-state analytical solution of the vibration isolation system,and the correctness is verified via the fourth order Runge-Kutta method and ADMAS. By using the force transmissibility as the indicator for evaluating the isolating performance,some comparisons are carried out among the proposed isolators. Meanwhile,according to the engineering application,the time-domain displacement responses of three types of isolating systems under multi-frequency steady excitation are solved,and a comparative study is carried out,respectively. The vibration power flow and maximum kinetic energy are investigated,and some typical design parameters are selected and analyzed. At last,from the perspective of the vibration dynamic absorber,the effects of the nonlinear connection on the vibration suppressing performance are further discussed. The calculation results show that the natural frequency of the vibration isolator can be decreased after the intermediate mass is introduced into the system,the effective vibration isolation frequency band of the vibration isolation system becomes wider,and an anti-resonance frequency is introduced at the original resonant frequency at the same time. Compared with the traditional three- parameter isolator and the nonlinear vibration isolator with an X-shaped mechanism,the vibration isolation performance of the developed isolator at both low and high frequencies is improved accordingly. In addition,the abovementioned all design parameters exist the optimal values when the force transmissibility of the nonlinear isolator is used as an evaluating index. Besides,the vibration suppressing performance of the vibration dynamic absorber with a grounded X-shaped mechanism is enhanced.
Key words:nonlinear analysis;isolator;harmonic balance method;intermediate mass;dynamic analysis
与传统两参数隔振器相比,三参数隔振器在阻尼元件上串联了辅助刚度元件,相当于整个系统与基础弹性连接.与传统两参数隔振器相比,可以在抑制共振峰的同时显著改善其高频隔振效果.三参数隔振器最早由Ruzicka等提出[1-1].王杰等[3-4]针对三参数流体阻尼器模型提出一种确定模型阻尼系数的机械阻抗等效理论与测试方法.王超新等[5]给出三参数隔振系统最优阻尼的设计方法,为后续微振动减振平台设计提供理论支持.
为了进一步提升隔振器的减隔振效果,非线性隔振器受到研究人员持续广泛的关注[6-9].一些研究人员将负刚度元件引入隔振系统中,使其具备“高静低动”的力学特性[10-13].Lorrain[11]将正负刚度并联的低频隔振原理用于隔振器和地震仪;Liu等[14]将欧拉压杆作为一种负刚度元件与线性弹簧并联安装在隔振系统中;王保励[15]利用水平弹簧连杆机构提供负刚度,提出一种具备仿生特征的非线性低频隔振器;刘彦琦等[16]利用两组倾斜布置的弹簧和一根竖直弹簧分别实现隔振系统的负刚度和正刚度特性;董光旭等[17]利用磁性负刚度弹簧与机械弹簧的组合设计实现系统超阻尼输出;邢昭阳等[18]以Voigt型动力吸振器为基础提出一种将杠杆机构应用于含负刚度弹簧元件的动力吸振器模型;Wang等[19]提出一种新型的负刚度放大阻尼器,并将其应用到地震工程研究中.因此,引入负刚度元件成为提升隔振器减隔振性能的热点研究方向之一.
除了负刚度元件可以提供非线性特性以外,一些具有特殊性能的结构/机构由于其自身优越的几何非线性特性也被广泛应用到减隔振系统中,例如:X形机构[20-23],薄片结构等.Liu等[24]充分利用X形机构的几何非线性特性,将n层X形机构与杠杆系统组合应用到被动隔振或者半主动隔振中,实现较好的低频宽带隔振.受到自然界中动物肢体形状的启发,Wu等[25]提出一种包含不同杆长和不同线性刚度的仿生结构.Bian等[26]、Feng等[27]提出一系列基于X 形机构的非线性隔振器,研究表明,X形机构可以利用自身的几何非线性特性對隔振系统的刚度和阻尼特性实现放大.Wang等[28]提出一种基于仿生学的垂直非对称X形隔振器,研究表明,此类非对称布置结构比对称布置的结构拥有更低的固有频率和传递率.刘海平等[29]、Liu等[30]基于传统三参数隔振器和X形机构在减隔振方面的优良性能,提出一种含几何非线性三参数隔振器模型.
在被动振动控制中,通过在隔振系统中增设质量元件,可以有效降低系统固有频率,并且改变系统原始的响应特征,使原有质量元件的共振转变为附加质量的共振,生成一个反共振频率,从而改善系统的低频隔振效果.
为了进一步改善内含X形机构非线性三参数隔振器在低频段的减隔振效果,本文提出一种含中间质量的改进三参数隔振器,并建立其动力学模型.在此基础上,利用谐波平衡法求解系统的频响特性,通过四阶龙格库塔法和多体动力学软件ADAMS对系统解析解的正确性进行验证.分析系统在不同质量比条件下的功率流特性以及最大动能,采用力传递率作为系统隔振性能的评价指标,通过与传统三参数隔振器和含X形机构非线性三参数隔振器进行对比研究,讨论了多频宽带稳态激励下不同类型隔振器的减隔振效果.在此基础上,针对该类隔振系统的多个关键设计参数开展影响分析.最后,从动力吸振器角度对X形机构非线性特征的影响展开讨论.相关工作可为新型隔振器设计奠定理论基础.
1含中间质量改进三参数隔振器模型
含中间质量改进三参数隔振器模型如图1所示.其中,弹簧kv为主支撑弹性元件,ke为辅助支撑弹簧,附加质量块m和X形机构依次串联.X形机构由4根长度均为l的刚性杆铰接组成,每根杆与水平轴的角度为θi,φ为刚性杆与水平轴的夹角变化量.阻尼元件c和刚度元件kh并联并以铰接方式与X形机构相连.此外,F代表系统所受外部激励力,y1和y2分别表示X形机构左右两侧活动铰接点在运动过程中发生的位移,x1和x2分别代表质量块M和m的位移.
为了方便比较,给出含几何非线性三参数隔振器模型以及传统三参数隔振器的模型,分别如图2 和图3所示.其中,kv和ke表示系统的刚度;c和M分别代表系统的阻尼和质量.以上4个参数均与含中间质量改进三参数隔振器相同.
2动力学建模及计算验证
2.1动力学建模
根据牛顿第二运动定律,建立隔振系统在力激励下的运动微分方程:
由图1可知,X形机构内部的几何关系为:
假设系统所受外部激励力F=F0cosωt,将式(2)中的几何关系代入式(1),可得:
为了简化计算,定义以下两个函数:
将函数f1(x2)和f2(x2)在x=0处分别进行三阶泰勒级数展开,可得:
其中,β0、β1、β2、β3、β4、β5的详细表达式如下.
将式(6)代入式(3)并忽略高次项,可得:
引入以下无量纲参量:
此处,采用谐波平衡法对系统进行求解,设u1和u2稳态解的形式为:
u1=u10cos(Ωτ+β)
u2=u20cos(Ωτ+ψ)(9)
将式(9)代入式(8),略掉高次项,并假设一次谐波项系数相等,可得:
定义A、B、C、D4个参数:
则系统在力激励条件下的幅频响应和相频响应分别表示为:
2.2计算结果验证
2.2.1与数值计算结果对比
为了验证含中间质量改进三参数隔振器所得解析解的正确性,利用四阶龙格库塔法给出系统的数值解并进行验证.
为了便于对比,根据参考文献[29]暂定kv=2 000 N/m,l=0.1 m,M=1 kg,c=1 Ns/m,γ1=kh/kv=0.05,γ2=ke/kv=3,θi=60°,μ=m/M=4.
隔振系统质量块M的位移幅频响应如图4所示.同时,图4中还给出相应模型的数值解.由图4可见,该隔振系统的数值解和解析解结果基本吻合.
2.2.2与仿真计算结果对比
为了进一步验证所建模型及解析解的正确性,利用多体动力学软件ADAMS进行仿真计算,所建模型如图5所示.利用ADAMS现有的铰接杆模型建立四杆结构,4个铰接杆两两铰接,且在其内部水平连接弹簧和阻尼单元,表征模型中的水平弹簧和阻尼;在四杆机构顶部铰接点与附加质量块铰接,并在该质量块上添加垂向移动副,在附加质量块与顶部矩形块之间连接一个弹簧,表征模型中的垂向弹簧ke;顶部质量块与底部质量块用弹簧连接,表征模型中的弹簧kv.
本部分仿真模型参数与2.2.1节相同.利用所建模型,在上端主质量施加激励幅值为1 N的正弦激励,计算得到质量块M在1~1 000 Hz频段内,步长为2 000条件下的位移响应,如图6所示.由图6可知,该隔振系统的解析结果与利用ADAMS仿真计算所得结果基本一致.
3不同类型隔振器隔振特性对比分析
3.1力传递率对比分析
用力传递率评价含中间质量改进三参数隔振器的隔振性能,采用简谐振动的叠加方式,得到传递到基础的力为:
传统三参数隔振器的力传递率Tf1和含中间质量改进三参数隔振器的力传递率Tf2分别为:
另外,含X形机构非线性三参数隔振器的力传递率参见文献[29].
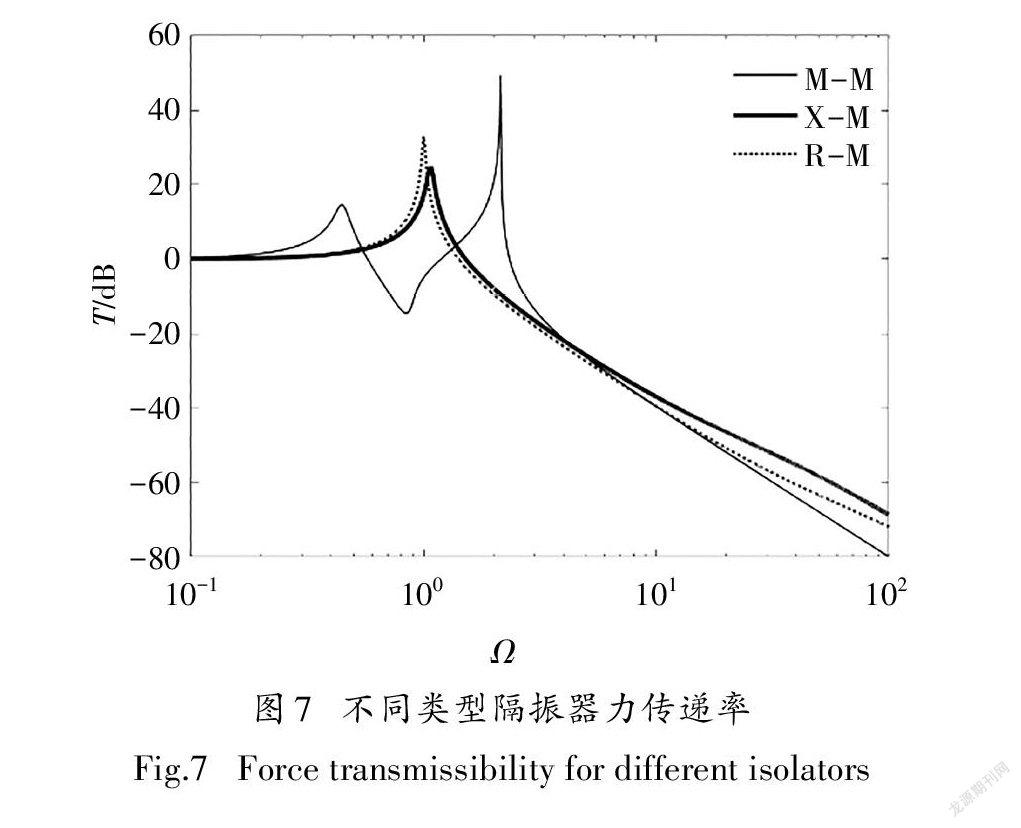
为了评价本文所提含中间质量改进三参数隔振器的隔振效果,将该模型与传统三参数隔振器(参见图3)和非线性三参数隔振器(参见图1)进行对比,具体设计参数分别为kv=2 000 N/m,l=0.1 m,M=1 kg,c=1 Ns/m,γ1=kh/kv=0.05,γ2=ke/kv=3,θi=60°,μ=m/M=4,3种隔振器中相同元件的参数相同.3种不同类型隔振器的力传递率计算结果如图7所示.图7 中“M-M”表示含中间质量改进三参数隔振器“X- M”表示非线性三参数隔振器“R-M”表示传统三参数隔振器.
由图7可知,与其他两种隔振器不同,含中间质量改进三参数隔振器可形成一个反共振频率.当激励频率等于反共振频率时,含中间质量改进三参数隔振器的隔振效果最好;当激励频率处于反共振频率附近时,含中间质量改进三参数隔振器的隔振效果明显优于传统三参数隔振器和非线性三参数隔振器.因此,可通过调整隔振器的设计参数,使反共振频率接近设备的振动频率,从而使隔振器最大限度地发挥减隔振效果.而且,受中间质量影响,隔振系统谐振频率向低频移动.
另外,与传统三参数隔振器相比,引入X形机构后非线性三参数隔振器的谐振振幅减小了8.64 dB,频率比由1增大到1.08,且在频率比约4.6~19.4频段内,含中间质量隔振器的传递率与传统三参数隔振器基本一致;在频率比大于19.4的隔振频段,含中间质量改进三参数隔振器的力传递率较低,证明在高频范围含中间质量隔振器的减隔振性能更优.
综上,受中间质量影响,三参数隔振器谐振频率向低频移动,在原隔振系统谐振频率附近的響应幅值显著减小,在高频段减隔振性能得到提升.
3.2时域特性对比分析
在工程实际中,系统所受的环境激励一般为多频宽带激励,为了研究含中间质量改进三参数隔振器的振动抑制效果,假设系统所受激励频率分别为22、34、42、52、63、71、85 rad·s-1.
图8给出含中间质量改进三参数隔振器在多频力激励条件下的时域位移响应曲线.由图8可知,在0~3 s内,传统三参数隔振器的最大位移响应幅值为8.4×10-3m,非线性三参数隔振器的最大位移响应幅值为5.3×10-3m,含中间质量改进三参数隔振器的最大位移响应幅值为1.3×10-3m.结合计算结果可知,与传统三参数隔振器相比,含中间质量改进三参数隔振器以及非线性三参数隔振器的隔振效果均有不同程度的提升.但是,含中间质量改进三参数隔振器的减隔振效果最优.
4含中间质量改进三参数隔振器动力学特性
4.1不同质量比对功率流与能量特性的影响
从系统内部振动能量分布情况出发,采用功率流方法评价隔振器对惯性质量动态响应的控制效果.在进行振动功率流特性分析时,往往对该隔振系统单位时间内的平均功率流进行求解计算.对于本文提出的隔振系统,采用刚性基础,在一个振动周期T=2π/Ω内,系统的无量纲平均输入功率与无量纲平均耗散功率相等.
系统的瞬时输入功率为系统输入的激励与系统响应的乘积,即
Pin=Pd=-u10Ωsin(Ωτ+α)f0cos Ωτ(18)
式中:Pin为系统的瞬时输入功率;Pd为系统的瞬时耗散功率.系统在单位时间周期内的无量纲平均输入功率与无量纲平均耗散功率可以表示为分贝的形式:
将本文所提隔振系统中的质量块M在正弦谐波激励下的最大动能以分贝形式表示:
图9和图10分别为不同质量比对应的功率流曲线和最大动能曲线.由图9和图10可以看出,改变质量比,对隔振系统在高频段及低频段处的动态特性无明显影响;但随着质量比不断增大,系统的功率流及最大动能曲线对应的两个峰值均向低频移动;随着质量比增大,两个峰值之间的低谷频率不断降低,两峰之间的频段逐渐变宽.
4.2不同参数对力传递率影响分析
重点针对在隔振器中引入中间质量后,阻尼比ζ、刚度比γ1和γ2、初始角度θi和质量比μ对力传递率的影响进行研究.初始设计参数与2.2.1节相同.
保持其他设计参数不变,选择不同初始阻尼比ζ对应系统力传递率,如图11所示.由图11可知,当阻尼比ζ=0时,在频率比Ω=1.2两侧出现新的谐振峰,且随着阻尼比增大谐振幅值减小;受中间质量影响,在频率比Ω=0.9附近,隔振系统的力传递率出现一低谷,且随着阻尼比增大谷值增大;阻尼比增大,隔振系统的第2个谐振峰的谐振频率向低频移动且频带变宽.当阻尼比大于0.84时,随着阻尼比继续增大,系统由于引入中间质量所产生的低谷逐渐消失.因此,阻尼比的最优值为[0,0.84].
仅考虑刚度比γ1变化对隔振系统力传递率的影响,如图12所示.由图12可知,当-1<γ1<0时,隔振系统中的水平弹簧呈现负刚度特征,此时系统的谐振峰对应的频率比Ω>2且仅呈现一个谐振峰;随着刚度比增大且大于0时,两个谐振峰出现在频率比Ω=1.6两侧,随着刚度比增大峰值增大,且第2个谐振峰对应的谐振频率向高频移动,频带变窄;在频率比Ω<3的高频范围,隔振系统的力传递率衰减特性良好.当刚度比γ1为[0.01,0.08]时,系统的低谷频率位于Ω=1附近,且对应位于低频段的第1个谐振峰值较小.因此,刚度比的最优值为[0.01,0.08].
考虑刚度比γ2变化对隔振系统力传递率的影响,计算结果如图13所示.由图13可知,当γ2=0时,隔振系统力传递率仅呈现一个谐振峰且对应的频率比Ω<1;随着刚度比γ2增大,第1个谐振峰对应的频率向低频移动,峰值逐渐降低;在频率比Ω>2附近出现另一个幅值较小的谐振峰,且该谐振峰的峰值增大,频带逐渐变宽,导致高频段的力传递率衰减效果变差;随着刚度比γ2增大,隔振系统受中间质量反共振特征影响出现的谷值增大.刚度比γ2存在最优值为[2,5],对应系统的低谷频率处于Ω=1附近.
图14给出不同初始角度θi对应隔振系统的力传递率.由图14可知,当初始角度为[0°,45°]时,隔振系统的力传递率在频率比Ω=1.2的两侧呈现出新的谐振峰以及反共振特征引起的谷值;当初始角度为[45°,75°]时,随着初始角度增大,位于低频段的第1 个谐振峰对应的频率向高频移动,且原有的两个谐振峰的峰值逐渐减小;当初始角度大于75°时,随着角度的进一步增大,中间质量引起的谷值减小,隔振系统仅呈现一个谐振峰且频带变宽,高频范围的力传递率衰减性能变差.因此,该初始角度的最优值为[45°,75°].
考虑隔振系统选择不同质量比μ对其力传递率的影响,如图15所示.由图15可知,当质量比μ<0.25时,系统存在2个谐振峰,第1个谐振峰出现在Ω=1处;当质量比μ>0.25时,频率比Ω=1处的谐振峰逐渐减小并逐渐消失,仅保留Ω=1的右侧的第2个谐振峰,峰值随着质量比的增大而增大.当质量比为[0.1,0.3]时,系统存在反共振特性,且2个谐振峰值较低.因此,质量比也存在最优值,为[0.1,0.3].
4.3非线性特征及连接方式对主振系动态响应特性的影响
在建立理论模型中,相对于主振系,中间质量及附属元件可视为动力吸振器.本节进一步讨论相比常规线性动力吸振器,X形机构引入的非线性特征及连接方式的变化对主振系动态响应特性的影响.
为了便于对比,给出安裝线性动力吸振器的系统动力学模型,如图16所示,并研究其受外部激励力F=F0cosωt时对应主振系的频响特性.其中,x1和x2分别为质量块M和m的振动位移,kv和ke均为线性弹簧,以上所有参数均与2.2.1节相同.
根据牛顿第二运动定律,安装线性动力吸振器系统受力激励的运动微分方程为:
引入以下无量纲变量:
计算得到主振系的位移幅值x10为:
图17为不同模型对应主振系的位移频响曲线. 其中“M-M”表示含中间质量改进三参数隔振器(参见图2)“T-M”表示安装线性动力吸振器系统(参见图16).为了便于对比,分别给出未安装动力吸振器系统模型(w/o VDA)和不考虑阻尼时对应含中间质量改进三参数隔振器(M-M,c=0)的主振系位移频响曲线.
由图17可知,安装动力吸振器后线性系统谐振频率附近峰值变为谷值,且在两侧引入新的谐振峰;受X形机构引入非线性特征影响,第1个谐振频率高于线性吸振器且峰值降低;考虑阻尼影响,连接X形机构动力吸振器引起的谐振峰值被进一步降低;第2个谐振频率对应峰值受X形机构(不含阻尼)影响较小,与安装线性动力吸振器对应频响结果相近;当考虑阻尼影响时,第2个谐振频率对应峰值得到有效抑制.除了上述谐振频率附近频段,在Ω<0.2的低频范围和Ω>4的高频范围不同模型对应频响曲线一致.
5结论
本文建立了含中间质量的改进三参数隔振器动力学模型,并进行了相关动力学特性研究,得到以下主要结论:
1)随着质量比不断增大,系统的平均输入功率流以及最大动能特性对应的两个峰值以及两峰之间的低谷向低频移动,且两峰之间的频段逐渐变宽.因此,增大质量比可以有效改善系统的隔振性能.
2)频域力传递率和时域位移响应对比表明,中间质量进一步改善了非线性三参数隔振器的减隔振性能,含中间质量的非线性三参数隔振器不仅可以改善系统的高频隔振性能,而且可以充分利用其反共振特性,使得激励频率为某一固定范围时的隔振性能显著提高.
3)在非线性三参数隔振器中引入中间质量,使隔振系统的固有频率向低频移动且原隔振系统的谐振峰受反共振特征影响而得到极大衰减;受中间质量影响,隔振系统各关键设计参数的影響主要集中于低频范围,且存在最优值.
4)将线性动力吸振器与接地X形机构连接,受其非线性特征影响,第1个谐振频率被提高且峰值得到有效抑制.
参考文献
[1] RUZICKA J E,CAVANAUGH R D. Elastically supported damper system provides a new method for vibration isolation [J]. Machine Design,1958,30(21):114-116.
[2] RUZICKA J E,DERBYTE. Influence of damping in vibration isolation [M]. Washington DC:Shock and Vibration Information Center,1971.
[3]王杰,赵寿根,吴大方,等.微振动隔振器动态阻尼系数的测试方法[J].航空学报,2014,35(2):454-460.
WANG J,ZHAO S G,WU D F,et al. A test method of dynamic damping coefficient of micro-vibration isolators[J]. Acta Aeronautica et AstronauticaSinica,2014,35(2):454-460. (In Chinese)
[4]王杰,赵寿根,吴大方,等.隔振器动力学参数的测试方法研究[J].振动工程学报,2014,27(6):885-892.
WANG J,ZHAO S G,WU D F,et al. A test method of dynamic parameters of vibration isolators [J]. Journal of Vibration Engineering,2014,27(6):885-892.(In Chinese)
[5]王超新,孙靖雅,张志谊,等.最优阻尼三参数隔振器设计和试验[J].机械工程学报,2015,51(15):90-96.
WANG C X,SUN J Y,ZHANG Z Y,et al. Design and experiment of a three-parameter isolation system with optimal damping [J]. Journal of Mechanical Engineering,2015,51 (15):90-96. (In Chinese)
[6]CARRELLA A,BRENNAN M J,WATERS TP,et al. On the design of a high-static-low-dynamic stiffness isolator using linear mechanical springs and magnets[J]. Journal of Sound and Vibration,2008,315(3):712-720.
[7]LEE C M,GOVERDOVSKIY V N. A multi-stage high-speed railroad vibration isolation system with “negative”stiffness [J]. Journal of Sound and Vibration,2012,331:914-921.
[8]HUANG X C,LIU X T,SUN J Y,et al. Vibration isolation characteristics of a nonlinear isolator using Euler buckled beam as negative stiffness corrector:a theoretical and experimental study[J]. Journal of Sound and Vibration,2014,333(4):1132-1148.
[9]HUANG X C,CHEN Y,HUA H X,et al. Shock isolation performance of a nonlinear isolator using Euler buckled beam as negative stiffness corrector:theoretical and experimental study[J]. Journal of Sound and Vibration,2015,345:178-196.
[10] MOLYNEUX W G. The support of an aircraft for ground resonance tests:a survey of available methods[J]. Aircraft Engineering and Aerospace Technology,1958,30(6):160-166.
[11] LORRAIN P. Low natural frequency vibration isolator or seismograph [J]. Review of Scientific Instruments,1974,45(2):198-202.
[12] ANTONIADIS I A,KYRIAKOPOULOS K J,PAPADOPOULOS E G. Hyper-damping behavior of stiff and stable oscillators with embedded statically unstable stiffness elements [J]. International Journal of Structural Stability and Dynamics,2017,17(5):1740008.
[13] ANTONIADIS I,CHRONOPOULOS D,SPITAS V,et al. Hyperdamping properties of a stiff and stable linear oscillator with a negative stiffness element[J]. Journal of Sound and Vibration,2015,346:37-52.
[14] LIU X T,HUANG X C,HUA H X. On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector[J]. Journal of Sound and Vibration,2013,332 (14):3359-3376.
[15]王保勵.一类几何非线性准零刚度系统的隔振理论与实验研究[D].哈尔滨:哈尔滨工业大学,2016:9-27.
WANG B L. Theoretical and experimental study on a class of geometrically nonlinear quasi-zero stifness vibration isolation system[D]. Harbin:Harbin Institute of Technology,2016:9-27.(In Chinese)
[16]刘彦琦,王好奎,黄庭轩,等.一种正负刚度并联低频隔振器的刚度和动力学特性分析[J].飞控与探测,2019,2(5):68-77.
LIU Y Q,WANG H K,HUANG T X,et al. Stiffness and dynamics analysis of a vibration isolator with positive and negative stiffness [J]. Flight Control & Detection,2019,2(5):68-77. (In Chinese)
[17]董光旭,张希农,谢石林,等.基于负刚度机构的高刚度-超阻尼隔振器设计与研究J].振动与冲击,2017,36(9):239-246.
DONG G X,ZHANG X N,XIE S L,et al. Design of a high stiffness and hyper-damping vibration isolator based on negative stiffness mechanism[J]. Journal of Vibration and Shock,2017,36 (9):239-246.(In Chinese)
[18]邢昭阳,申永军,邢海军,等.一种含放大机构的负刚度动力吸振器的参数优化[J].力学学报,2019,51(3):894-903.
XING Z Y,SHEN Y J,XING H J,et al. Parameters optimization of a dynamic vibration absorber with amplifying mechanism and negative stiffness[J].Chinese Journal of Theoretical and Applied Mechanics,2019,51(3):894-903.(In Chinese)
[19] WANG M,SUN F F,YANG J Q,et al. Seismic protection of SDOF systems with a negative stiffness amplifying damper[J]. Engineering Structures,2019,190:128-141.
[20] SUN X T,JING X J,XU J,et al. Vibration isolation via a scissorlike structured platform[J]. Journal of Sound and Vibration,2014,333(9):2404-2420.
[21] SUN X T,JING X J. Analysis and design of a nonlinear stiffness and damping system with a scissor-like structure[J]. Mechanical Systems and Signal Processing,2016,66/67:723-742.
[22] LIU C C,JING X J,CHEN Z B. Band stop vibration suppression using a passive X-shape structured lever-type isolation system[J]. Mechanical Systems and Signal Processing,2016,68/69:342-353.
[23] WU Z J,JING X J,SUN B,et al. A 6DOF passive vibration isolator using X-shape supporting structures[J]. Journal of Sound and Vi- bration,2016,380:90-111.
[24] LIU C C,JING X J,LI F M. Vibration isolation using a hybrid lever-type isolation system with an X-shape supporting structure[J]. International Journal of Mechanical Sciences,2015,98:169-177.
[25] WU Z J,JING X J,BIAN J,et al. Vibration isolation by exploring bio-inspired structural nonlinearity[J]. Bioinspiration &Biomi- metics,2015,10(5):056015.
[26] BIAN J,JING X J.Superior nonlinear passive damping characteristics of the bio-inspired limb-like or X-shaped structure[J]. Mechanical Systems and Signal Processing,2019,125:21-51.
[27] FENG X,JING X J,XU Z D,et al. Bio-inspired anti-vibration with nonlinear inertia coupling[J]. Mechanical Systems and Signal Processing,2019,124:562-595.
[28] WANG Y,JING X J,GUO Y Q. Nonlinear analysis of a bioinspired vertically asymmetric isolation system under different structural constraints[J]. Nonlinear Dynamics,2019,95(1):445-464.
[29]劉海平,申大山,赵鹏鹏,非线性三参数隔振器动力学特性研究[J].振动工程学报,2021,34(3):490-498.
LIU H P,SHEN D S,ZHAO PP. Dynamic performance of a three- parameter isolator with nonlinear characteristic[J]. Journal of Vibration Engineering,2021,34(3):490-498.(In Chinese)
[30] LIU H P,ZHAO P P. Displacement transmissibility of a four- parameter isolator with geometric nonlinearity[J]. International Journal of Structural Stability and Dynamics,2020,20(8):2050092.
