挖掘素材价值 探索解题通法*

杨春霞

(江苏省南京市第二十九中学初中部 210003)

诸士金

(江苏省南京市横梁初级中学 211515)

在解题教学中，部分教师只是教给学生具体的解法，而对问题的数学本质揭示得不够全面.选取有价值的试题素材，有策略地进行解题教学，让解题思路有迹可循，让学生有法可依、学会解题通法，应是解题教学的价值诉求.笔者以在中考复习教学中遇到的一道2021年南京市中考填空压轴题为例，进行有关解题教学的思考.

1 问题呈现与价值分析

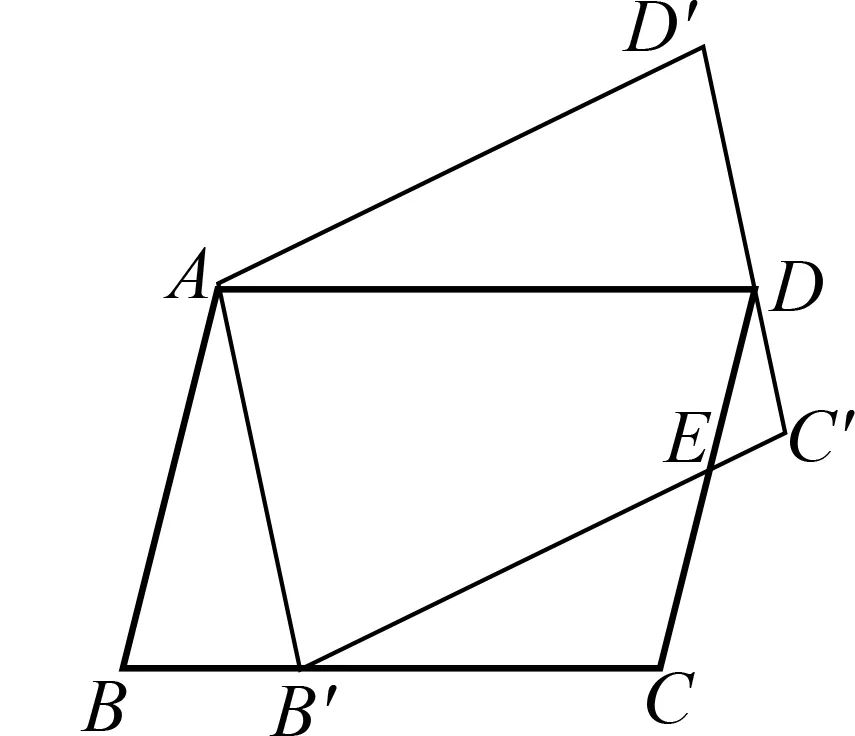
图1

本题以平行四边形为基础图形，通过旋转变换进行构图，呈现形式简洁优美，题小意长.试题立足几何核心知识，综合考查了平行四边形的判定与性质、图形运动的相关性质、相似三角形的判定与性质、全等三角形的判定与性质以及方程(组)思想等初中数学的主要知识点.考查内容较为全面，需要学生借助几何直观和空间想象感知平行四边形在旋转变换过程中的“变”与“不变”，厘清图形局部元素中角、线段之间的关系，并能在较为复杂的模型中把握图形整体之间的关联，构建解决数学问题的有效模型，形成有条理、合乎逻辑的解题路径.试题在解法上贯彻了求线段长度的通性通法，教师可以通过类似素材的解题教学，培养学生的数学思维和理性精神.

2 解法分析与通法探究

图2

此题是一道填空题，题型虽小，难度却不小.进行小题大做，深挖素材隐含的数学知识与解题方法，才能凸显其教学价值.本题点B′落在BC上，则点D恰好落在D′C′上，看似巧合，实则必然.这点可以利用同一法简要说明：如图2，连结DD′，易证△ABB′∽△ADD′，故∠B=∠AB′B=∠ADD′=∠AD′D.又∠B=∠AB′C′,且∠AB′C′=∠AD′C′,所以∠AD′C′=∠AD′D,即点D在线段D′C′上.

由点B和点D位置的特殊性，使得图形整体关系丰富，能够产生很多相似图形.因此本题的构图视野宽、解题路径广，宜为教学所用.下面从相似基本图形的角度出发，进行解法分析与通法探究.

2.1 基于相似基本图形“X型”构图

在寻找或构造相似三角形模型时，常见的X型构图求线段长是一个思考方向.本题首先可以线段CE所在三角形△B′CE为直接研究对象，尝试寻找或构造与之成X型相似的基本图形.

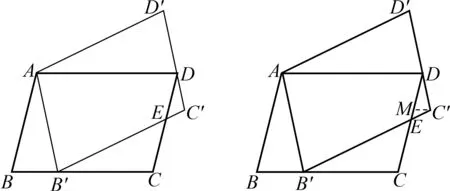
图3 图4

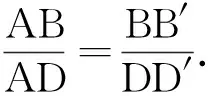
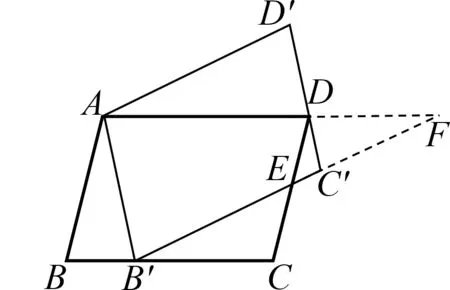
图5

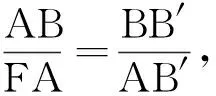
分析本题由旋转容易想到的是△ABB′与△ADD′相似，从而可得线段DD′和DC′的长度，后面很多方法都会用到DD′和DC′的长，不再赘述.方法1以CE为研究对象，从直观上感知△DEC′与△B′EC呈X型相似，根据相似的性质，构建比例式进行求解.值得注意的是，这里的比例式其实隐含的是两个关于EC和EC′的二元一次方程，对学生的代数推理能力和运算能力要求较高，很多学生会被这两组比例式困住，难以得解.方法2和方法3均以CE所在的△B′CE为对象，分别过点C′和点D作辅助线，得到两组相似.虽然需要构造相似，但计算难度比方法1要小，因此各有千秋.

2.2 基于相似基本图形“A型”构图

A型相似也是常见的相似基本图形.本题构造A型图可以把CE所在的三角形△B′CE，或DE所在的三角形△DCE作为研究对象，寻找或构造与之成A型相似的基本图形.

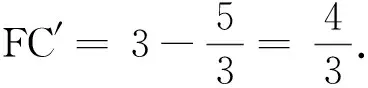
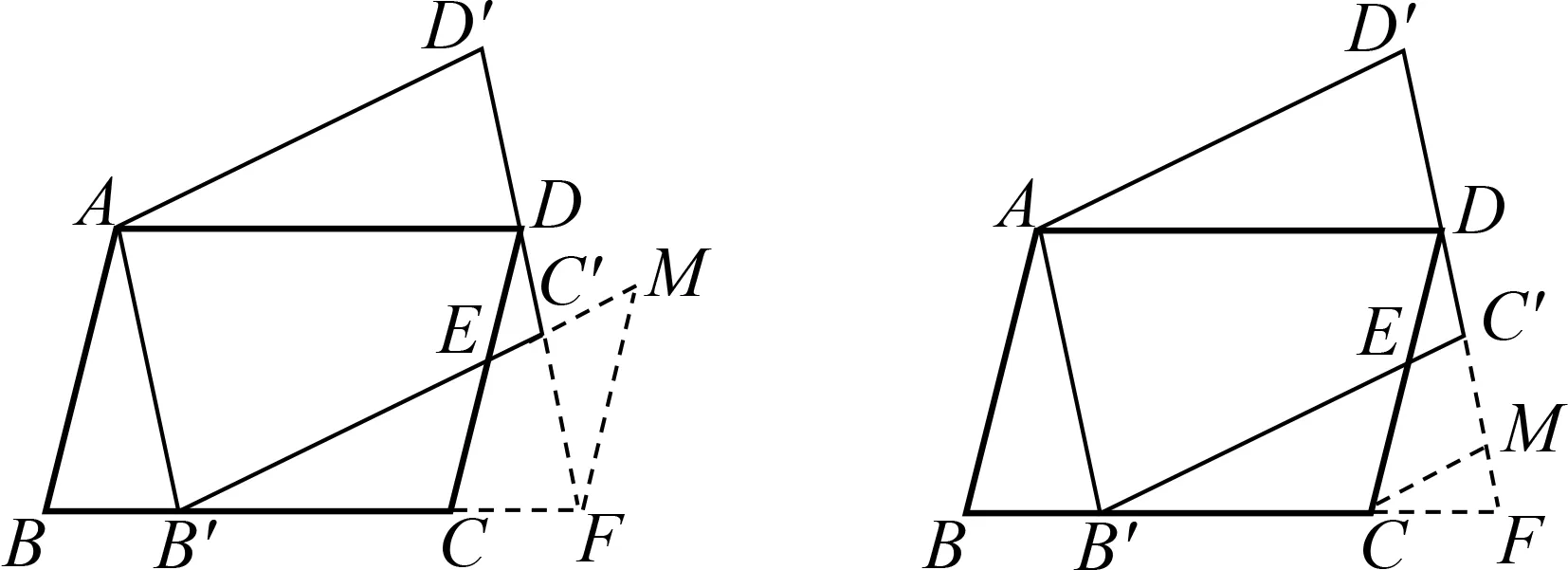
图6 图7

图8

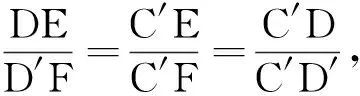
分析方法4～方法6都是构造A型相似，但构造的思路不一样.方法4直接以CE边为研究对象，在△B′EC的外部，即B′E和B′C的延长线上构造，其中点F的确定是思维上的一个难点，需要结合图形整体感知，选择出这样的一个特殊点.方法5则以与CE相关的线段DE为研究对象，在△DEC′的两边DE和DC′的延长线上过点C构造“A型”.与方法5不同之处在于，方法6是在△DEC′的另两边C′E和C′D的延长线上过点D′构造“A型”.

2.3 基于“一线三等角”模型构图

审题时可以发现，∠ABB′=∠AB′C，且这两个角的顶点在同一条直线上，由直观感知和已有的构图经验，容易想到“一线三等角”模型.因此，可以尝试从“一线三等角”的基本图形出发，构造相似来求线段长.

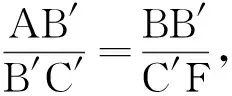
图9 图10

图11

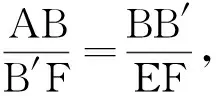
分析方法7是从右下角向构造一线三等角模型靠拢，形成以BC为一线，∠B=∠AB′C′=∠B′FC′为三等角的模型，得到△ABB′与△B′FC′相似解决问题.方法8和方法9同样是基于“一线三等角”模型，分别过点C和点E作平行来构造相似.

2.4 基于补全平行四边形构相似

在构造“一线三等角”的过程中，“一线”托住了三个“等角”，这样的直观构图感知在本题解法探究中还可以带来不一样的启示，比如用“一线”托住凸出的角，将其补全为一个平行四边形.

图12

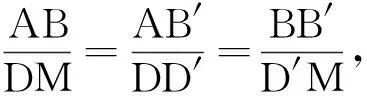
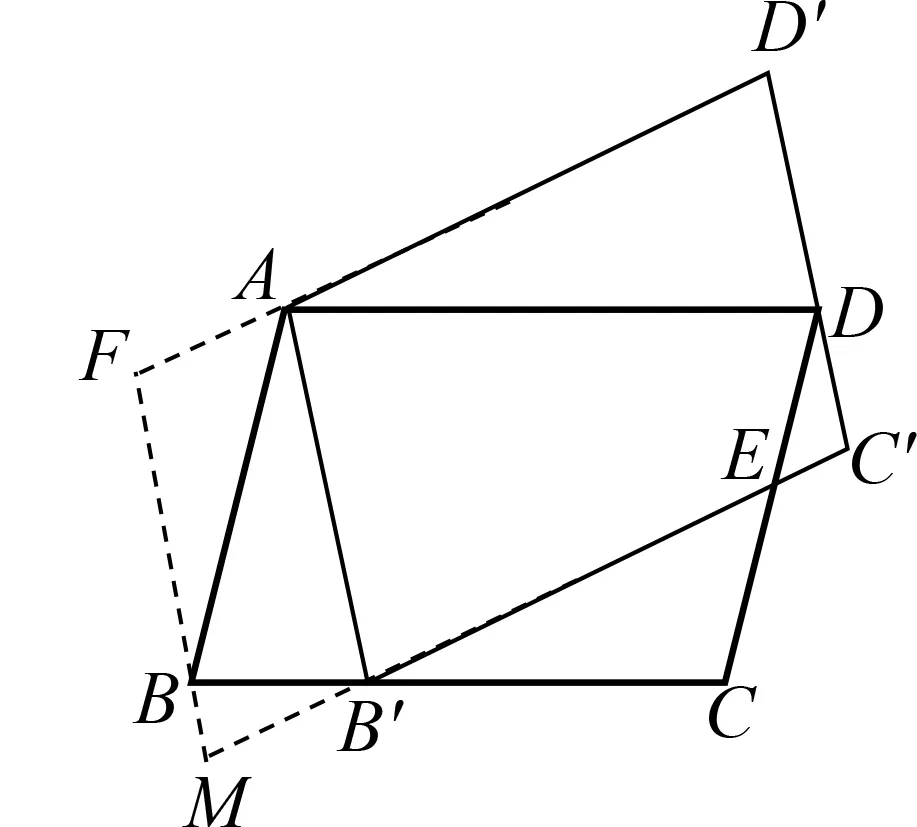
图13

分析方法10在点D′处作平行补全了平行四边形，往一线三等角模型方向去靠拢，但在靠拢中却发现，此处并不是一线三等角，而是一线二等角，柳暗花明又一村，∠M=∠ADD′为证明三角形相似提供了新的思路.类似地，也可以在点B、点C及点C′处补全平行四边形，构造图13～ 图15进行解决.这四种方法均是通过构造平行四边形，形成一线二等角的模型，然后再寻找三角形相似，建立线段比例关系求得CE长.

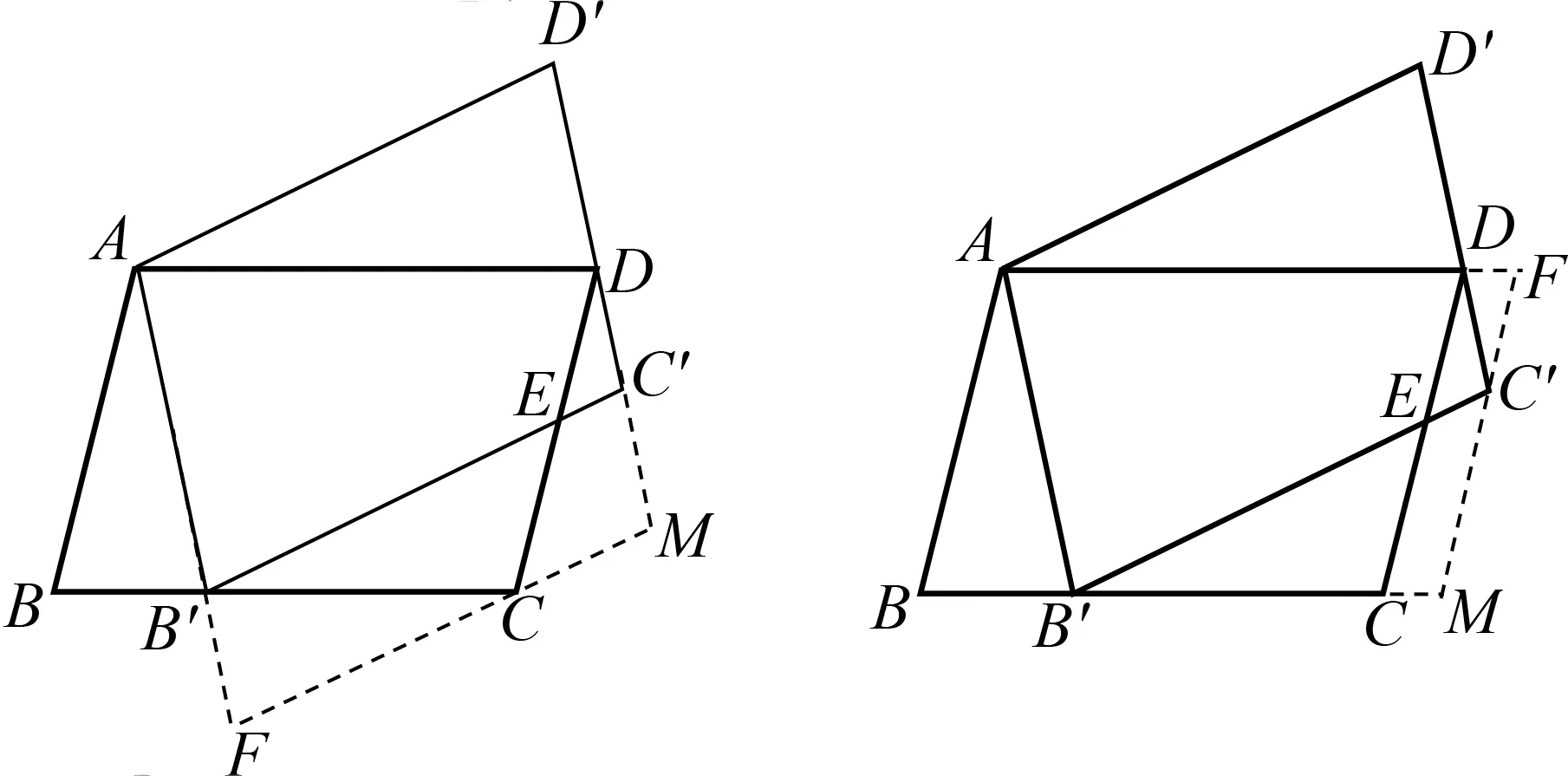
图14 图15

2.5 基于平移转化构相似

在方法1的分析中，我们知道△ABB′∽△ADD′是比较容易发现的，而要求线段CE的长，思考CE所在△B′CE与△ADD′的关系也是联想的一个自然方向.因此，能否在△ADD′内寻找或构造与△B′CE相似的图形呢？这里借助图形变化中的平移缩放就可以得到如下的方法.

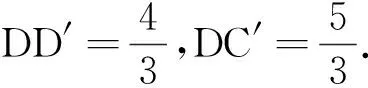
图16 图17

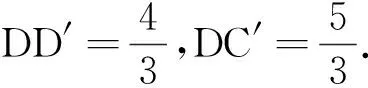
分析方法11与12的解题思路类似，均源于通过平移缩放构造与△B′CE相似的直观感知.在几何解题中，与相似的几种常见基本图形一样，平移缩放也是相似构图的一个重要切入点.方法11、12都是将△B′CE往上平移缩放与△ADD′进行相似构图，不同的是，一个是以AD为对应边构图，另一个是以AD′为对应边构图.

3 解题启示与教学建议

在解题教学中，既要让学生知其然，更要让学生知其所以然，注重解题思路的探寻过程，积累思维活动经验.引导学生经历怎样审题、怎样想到思路方法、为什么要这样想、还可以怎样想的过程，通过对一道题目的讲解，达到做一题通一类的效果，这是解题教学的价值所在.本题解法丰富，从其中任何一种相似的基本模型出发，都能自然产生解题路径.而解法的自然生成，需要我们在平时的几何解题教学中注重培养学生的发散联想、模型意识和结构化思想，让学生想得到、想得通、想得妙！

3.1 关注发散联想，弄清怎么想

怎么做固然重要，怎么想更为重要.波利亚告诉我们，解题离不开最近联想，从条件出发，从问题出发，从知识点出发，从数学基本模型出发，都是可以进行联想的方向.教学中要多鼓励并指导学生学会从上述方向发散思维，进行联想.比如，由本题已知条件出发进行最近联想，你可以初步得到哪些结论？整合条件和问题进行进一步联想，要求线段CE的长需要做什么？再比如，从旋转这一知识点出发，你可以得到什么？从基本模型出发，本题图形中你又发现了哪些常见的基本图形？由此获得更多的需知对象.数学是思维的体操，解题教学中要引导学生进行最近联想，学会用数学的方式发散思维，提高数学思维能力，积累解题活动经验.

3.2 关注数学模型，聚焦怎么做

在本题的解法探索过程中可以发现，解题路径的自然生成离不开数学的基本模型.本题几乎覆盖了相似图形中所有常见的基本图形，一是基于相似基本模型，往熟悉的基本图形X型、A型构造相似；二是基于相似的经典模型，往“一线三等角”构造相似；三是基于空间想象，借助补全平行四边形构造相似；四是基于几何直观，借助图形平移变换构造相似.从每一种相似基本图形出发均可找到解题方向，成功抵达，从而形成多样的解法.因此，在平时的教学中，教师应强化学生的数学建模意识，一方面要共同归纳常见的几何模型，深刻理解模型的关键特征；另一方面要引导学生有意识地从复杂的图形中分解出或补全为常见的基本图形，从而把陌生的、复杂的问题转化为熟悉的、简单的问题，提高学生的模型意识和利用模型解决问题的能力.

3.3 关注知识结构，重视回头看

数学的解题研究看似解决一个问题，实则要教给学生思考问题的方式，由一个问题打通知识间的内在关联，将碎片化的知识结构化，形成解决问题的通性通法，从而解决更多问题.本题目标是求线段CE的长度；对于线段求长问题，在整个初中阶段有很多方法，如利用线段和差、倍数等数量关系求长，利用勾股定理三边关系求长，利用全等三角形的相等关系求长，利用相似三角形的比例关系求长，利用三角函数边角关系求长等，这些方法串联起来就形成了一个线段求长的知识链条，也就是线段求长的通法.而本题利用相似求线段CE的长度即是这个知识链条中的一个知识节点.解题教学中，要引导学生梳理这样的知识与方法链条，从而形成知识结构网.对于解决问题的通性通法，需要引导学生不断地总结和回顾反思，才能让学生在遇到新的问题时有法可想、有路可走，进而培养学生的数学高阶思维，形成自主探究问题的解题经验.

波利亚曾说：“如果你希望从自己的努力中取得最大的收获，就要从已经解决了的问题中找出那些对处理将来的问题可能有用的特征.”[1]本题已经尘埃落定，但其解法的探究给几何解题的教与学带来了很多启示.解题即是缩小差距，缩小差距就是使已知与未知互相靠拢，我们在追求缩小差距的抵达，我们更是在享受一场互相靠拢的旅程，最终实现那美妙的双向奔赴.