面向高密度聚乙烯生产过程的最优采样策略

尹 鹏, 陈伟锋

(浙江工业大学 信息工程学院, 浙江 杭州 310023)

1 前 言

高密度聚乙烯(high-density polyethylene，HDPE)是5 大通用合成树脂之一，具有优异的化学稳定性和耐低温性。我国是HPDE 最大消费国，也是最大进口国[1]，2019 年消费量为15 478 kt，其中进口7 997 kt，产品自足率为49.39%。目前我国HDPE 产品结构矛盾突出，中低端产能过剩，高端产品仍以进口为主。高密度聚乙烯实际上是混合物，由不同链长的高分子聚合物组成，组成成分不同会带来不同的材料特性，为对聚合物材料特性进行表征，质量分数的分布常常作为质量指标。质量分数的分布为所有不同链长分子质量占聚合物总质量的分数，它可以反映产品的微观性质[2]。高密度聚乙烯模型的开发对提升产品的质量有极为重要的意义，而参数估计是实现基于质量分数分布的高密度聚乙烯建模的核心技术手段之一。

机理模型在反应过程的设计、优化和控制中起着重要的作用，参数估计是建立过程模型的关键组成部分。然而，由于参数可识别性和可估计性的问题，高质量参数值的估计并不容易[3]。从另一个角度来看，参数估计问题往往是不定的，即不是所有的参数都可以唯一确定。常用的方法是通过将其他参数固定在合理的值上来估计参数的一个子集，而难点就在于确定可估计性高的参数子集。Yao 等[4]对参数子集选择方法进行了研究，其中正交化方法具有明显的几何含义并且易于实现，它将灵敏度矩阵S正交化排序，可以看作是每一步骤的D 准则最大化的顺序方法，有效性被Chu 等[5]证明。正交化方法是参数子集选择中应用最广泛的技术[6-9]，缺点是很难设置一个适当的投影向量范数阈值来分离可估参数和不可估参数。Machado 等[10]基于费雪信息矩阵(Fisher information matrix, FIM)准则进行参数子集选择，通过枚举法评估每个参数子集，此外还有行列式准则和一个修正的E 准则之间的比率 (a ratio between a determinant criterion and a modified E criterion，RDE)准则，但是随着参数数量上升，将会面临组合爆炸的问题。Brun等[11]提出了相关性和共线性方法选择参数子集，通过灵敏度矩阵S的列中的线性关系来确定不可估计的参数。Jolliffe 等[12]提出主成分分析法(principal component analysis，PCA)，利用STS或者FIM 的特征值来选择参数子集，缺点在于很难将特征值与特定的参数相匹配。此外Chen 等[13]提出用简约海森矩阵(reduced Hessian,Hr)代替FIM，并且证明了等效性，避免了灵敏度矩阵S的计算，并基于系统输出对参数进行排序，同时引入了关于待估参数的标准差与估计值比率(ratio of standard deviation to estimated value，RSDEV)准则用于可估和不可估参数的划分。

基于模型的实验设计(design of experiments，DOE)的目标是设计最佳的系统输入，并以经济的方式使收集到的输出中包含尽可能多的系统信息以便于后期的参数估计，采样时间的选择是DOE 的一个重要组成部分，特别是在实验和样本分析成本高昂的情况下。有很多文献的最优采样使用了FIM 的A 准则、D准则，E 准则[14～16]，但是在参数之间存在高相关性的情况下，A 准则是不可靠的，而D 准则往往过于重视敏感参数[17]。Kutalik 等[18]提出了一种次优采样时间选择方法，该方法是假设在选择采样时间之前，通过一些时间点进行参数估计，基于多重打靶法最大化FIM 的行列式来选择采样时间。结合基于扩展灵敏度状态方程系统的优化采样设计和有限元的变化，Hoang 等[19]提出了一种先进的采样策略，优点是直接计算控制变量的参数灵敏度的精确高阶导数，并且使用联立求解。Chen 等[20]基于RSDEV 准则，提出一种迭代增强的近似最优的时间序列采样策略。

HDPE 模型十分复杂，使用自适应步长计算灵敏度矩阵S[21]时，无法使用同一步长计算多个点的灵敏度信息，这使得灵敏度矩阵S的计算成本过于巨大，导致无法使用与S相关的方法去选择参数子集，同时也无法对模型中参数排序。因此本研究采用了Chen 等[13]提出的Hr矩阵代替FIM，并且结合RSDEV准则选出可估计参数子集，继而提出了一种基于拉丁超立方体采样的最优采样策略，结合RSDEV 准则与Hr的关系建立了混合整数非线性规划(mixed integer nonlinear programming，MINLP)模型，并使用了一种新的迭代增强近似最优采样策略。数值结果表明，在RSDEV 准则约束条件下，可以显著降低采样个数，同时得到可以接受的待估参数的相对误差。

2 高密度聚乙烯生产过程模型

HDPE 由于生产成本低、机械和流变性能广泛，是应用最广泛的合成商品聚合物之一[22]。多活性位Ziegler-Natta 催化下的HDPE 聚合反应是HDPE 生产的重要工艺，聚合物在催化剂的活性位点生长，直到链转移发生，从而形成死聚合物链[23]。

考虑模型基于在连续搅拌釜反应器(continuous stirred tank reactor，CSTR)中进行的HDPE 浆工艺，由乙烯(单体)、氢气(链转移剂)、正己烷(稀释剂)和Ziegler-Natta 催化剂系统构成，其中四氯化钛(TiCl4)作为催化剂，三乙基铝(Al(C2H5)3)作为助催化剂，连续注入CSTR，并且将浆液产物连续从反应器中去除。假设各个活性位吸附单体的能力相同，则链增长、链转移和链失活的动力学常数与链的长度无关[24]。Ziegler-Natta 催化剂的不同活性位点具有不同的传播速率常数，会产生很多不同链长的聚合物，从而导致一个非常宽广的质量分数的分布。建立一个由大量微分和代数方程(differential-algebraic equation，DAE)组成的联立方程模型，以描述该过程的动力学和质量分数的分布。

从过程控制的角度来看，可用的操纵变量为催化剂、助催化剂、单体、氢、六烷的供给量和反应器温度，而被控变量为单体转化率和质量分数的分布。

2.1 乙烯聚合反应机理

乙烯聚合反应采用的催化剂是Ziegler-Natta 催化剂，是一种复合催化剂。乙烯聚合反应机理包括催化剂活化、链引发反应、链增长反应、链转移反应以及链失活反应[25]。

1) 催化剂活化。通过Al(C2H5)3对钛进行烷基化形成活性位点，反应如下：

式中：CP(j)为具有潜在活性位点的催化剂TiCl4；A 为助催化剂Al(C2H5)3；kaA(j)为催化剂活化反应的动力学常数，L·(mol·s)-1；j为活性位编号；P0(j)为具有还未聚合任何单位的空活性位点的催化剂。

2) 链引发反应。单体分子与活性中心相互反应形成链长为1 的聚乙烯链，反应如下：

式中：M 为单体；ki(j)为链引发反应的动力学常数，L·(mol·s)-1；P1(j)为链长为1 且仍具有活性位点的乙烯聚合物链。

3) 链增长反应。继续插入乙烯单元使链长不断增长，反应如下：

式中：kp(j)为链增长反应的动力学常数，L·(mol·s)-1；Pn(j)为链长为n的活聚合物链。

4) 链转移反应。活聚合物链分别与单体、氢气、助催化剂反应及自反应形成死链，反应如下：

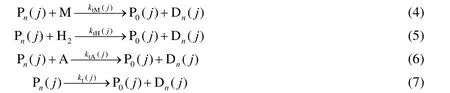
式中：ktM(j）为向单体转移链反应的动力学常数，L·(mol·s)-1；ktH(j）为向氢气转移链反应的动力学常数，L0.5·(mol0.5·s-1)；ktA(j）为向助催化剂转移链反应的动力学常数，L·(mol·s)-1；kt(j）为自转移反应的动力学常数，s-1；Dn(j)为链长为n的死聚合物链。

5) 链失活反应。活聚合物链与活性中心全部失活，反应如下：

式中：kd(j）为自失活反应的动力学常数，s-1；Cd(j)为具有不能再聚合任何单体的死活性位点的催化剂。

在这个模型中，活性位点的数量被设为2，根据乙烯聚合反应机理，转移终止的伪动力学速率系数定义为

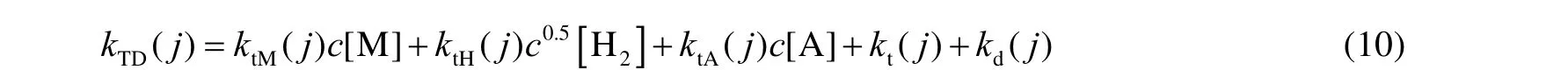
式中：c[·]为括号中某成分的浓度，mol·L-1。

2.2 物料衡算

为了简洁起见，模型中将在第j个活性位点的活和死聚合物的m阶矩分别定义为

活聚合物链的零阶矩表示为

对于长度为n=1 的活链，反应净生产率为

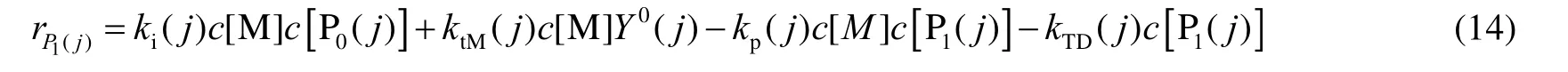
对于长度n≥2 的活链来说，反应净生产率为

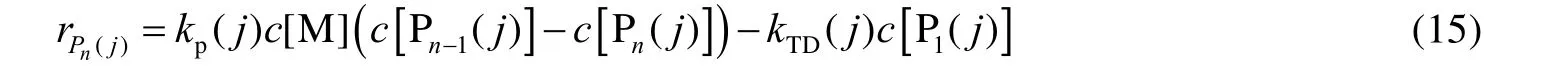
同样地，长度为n=1 和n≥2 的死链的反应净生产率分别为

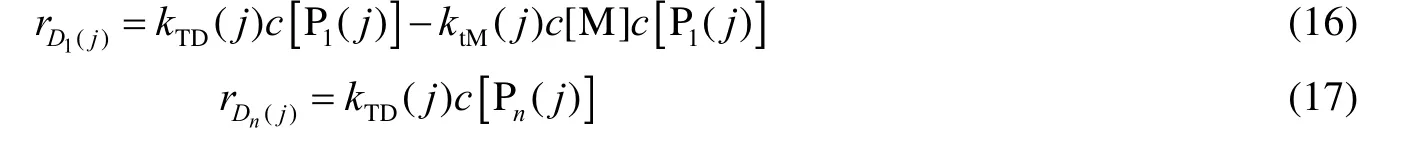
从式(14)～(17)可得，长度n=1,2,3,…,nmax的活链和死链的粒数衡算方程分别为

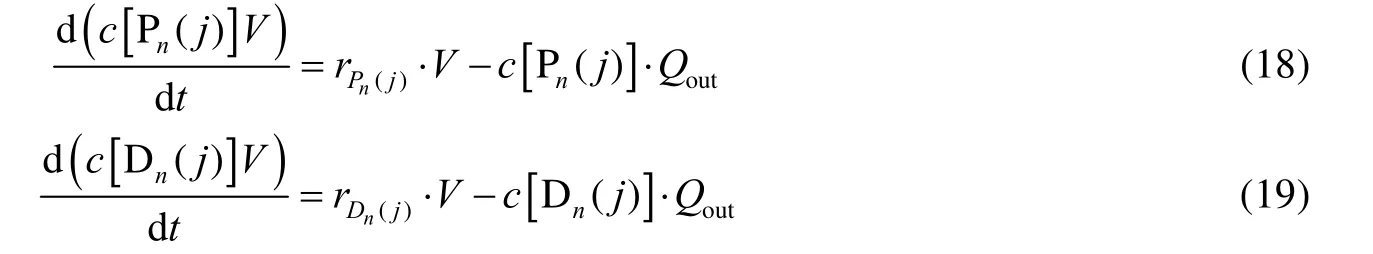
式中：Qout为体积流出率，%；V为反应堆的液体体积，L。类似的单体、氢气、己烷、催化剂潜在活性位点、催化剂无活性位点、活性点、共催化剂以及活聚合物链的零阶矩和一阶矩的物料衡算方程也可以写为

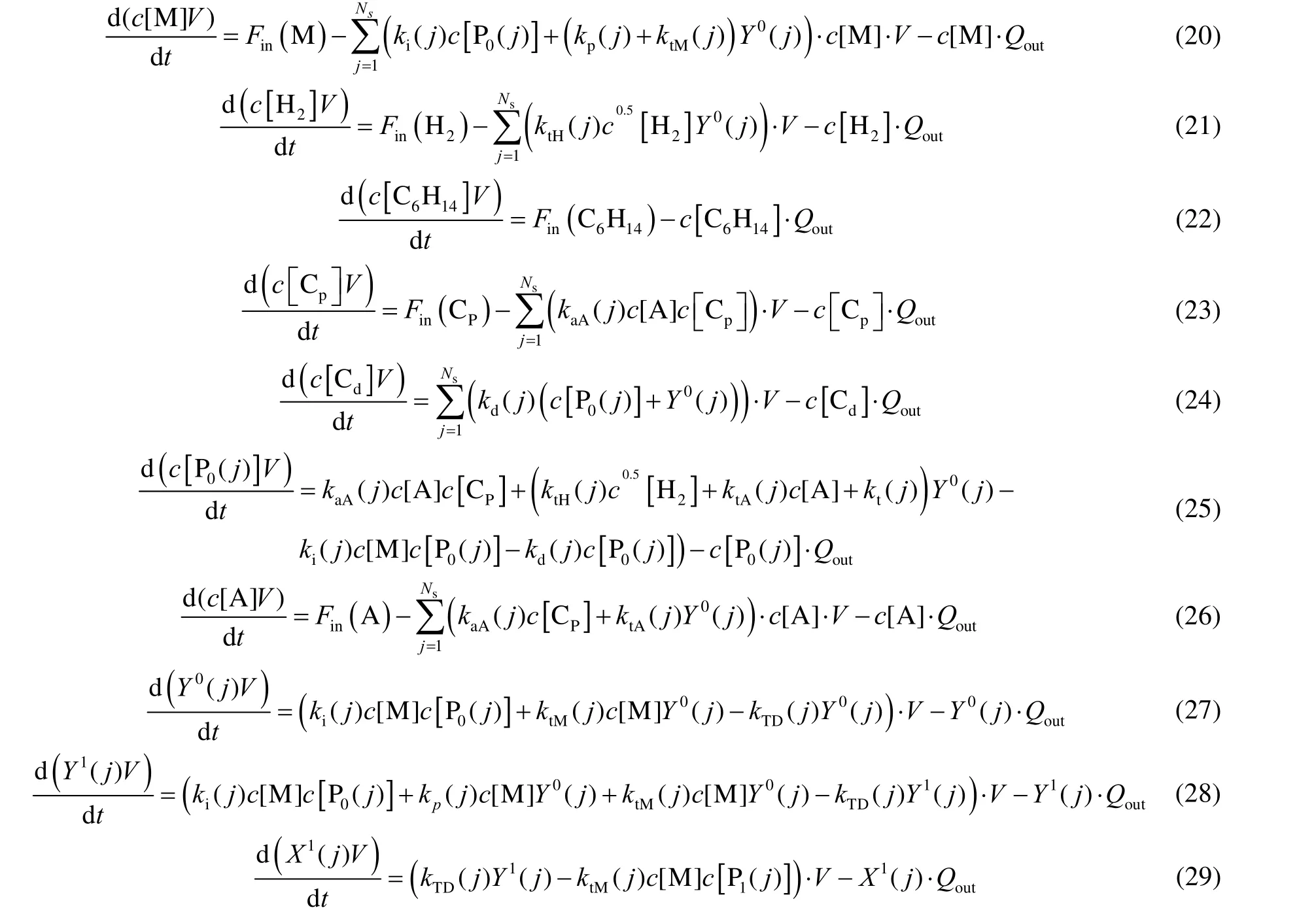
式中：Ns为活性位点个数，Ns=2；Fin(M)、Fin(H2)、Fin(C6H14)、Fin(CP)、Fin(A)分别为M、H2、C6H14、CP、A 的摩尔进料流率，mol·h-1。

Ma 等[26]提出一种利用二维正交配置的质量分数分布重构方法，以捕捉质量分数分布的时间动态特征和链长度的分布特征。采用联立配置法离散化模型，将模型最终离散成具有86 116 个变量，86 100 条等式约束的大型非线性规划(nonlinear programming，NLP)问题。16 个待估参数分别为kp(1)、kp(2)、ktH(1)、ktH(2)、ktM(1)、ktM(2)、ktA(1)、ktA(2)、kaA(1)、kaA(2)、ki(1)、ki(2)、kt(1)、kt(2)、kd(1)、kd(2)。模型采用以下目标函数进行参数估计：

式中：2σ为测量噪声的方差，tf为时间采样点，wcal为模型质量分数的分布仿真值，wrel为模型质量分数的分布实际值。

3 最优采样

由于HDPE 采样后的分析成本过高，故尽可能减少采样数量，同时尽量获得多的信息，本研究将结合RSDEV 准则和FIM 的A 准则来选择参数子集，然后基于拉丁超立方体采样，使用Chen 等[20]提出的一种基于Hr的近似最优的时间序列采样策略。

3.1 参数子集选择

在参数子集选择方法上，Chen等[13]证明了Hr与FIM的等效性，故采用Hr代替FIM，并且将基于FIM准则选择参数子集。常用的FIM准则包括了A准则、D准则、修正后的E准则，此外还有RDE准则，如果参数数量太多，则会面临组合爆炸问题，为避免此问题，采用Chen等[13]提出的RSDEV准则，即

式中：δq为第q个待估参数标准差；qθ为第q个待估参数的估计值；ε为比率；δq=aq,q1/2，aq,q为相应参数的协方差矩阵A的对角元素的值，即A矩阵的第q个对角元素，A=FIM-1=Hr-1。

将FIM 的A 准则和RSDEV 准则结合在一起形成新的准则：

min (tr (FIM-1))，且满足max (ε)<εexp。式中：εexp为期望的比率阈值。

3.2 最优采样策略

将HDPE 模型表达成微分代数方程组，即

式中：K为插值的阶次，也是配置点的数量，xik为在第i个有限元的第k个配置点的状态变量向量，yik为在第i个有限元的第k个配置点的代数变量向量，τ为有限元中t的相对值，kτ、jτ分别为有限元中第k、j个配置点t的相对值。在第l个采样时间点tl处的预测可以用以下方程来近似：

式中：zl,cal为采样时间点tl处的模拟预测向量。

假设一个{1,…,ntp}的时间序列，它可以作为潜在的采样点，相应在tl的测量是zl，l=1, …,ntp。基于似然原理，假设z的每个分量的测量噪声呈正态分布，均值为0、方差为σp2，p=1,…,nz，通过求解问题(35)可以估计θ：

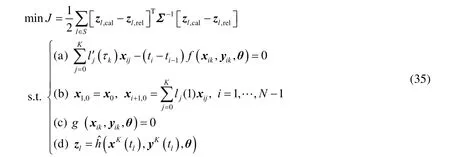
式中：zl,rel为采样时间点tl处的实际预测向量，Σ为对角线方差矩阵，其中第p个元素为σp2；l j′(kτ)为导数。

设S={t1,t2,…,tn}是采样点集合，是时间序列{1,2,…,ntp}的一个子集。为了便于最优抽样分析，将S={1,2,…,ntp}，并且将非线性规划问题(35)中的离散变量和方程被重写为

式中：I为单位矩阵。

确定δq/θq的值，即参数q的标准差除以其估计值，建立一个MINLP 问题寻找输出测量时间序列的最小子集，从而可以找到一个满足上述比率的A矩阵。

首先定义了Zr，它由Z的最后一个nz×ntp行组成：

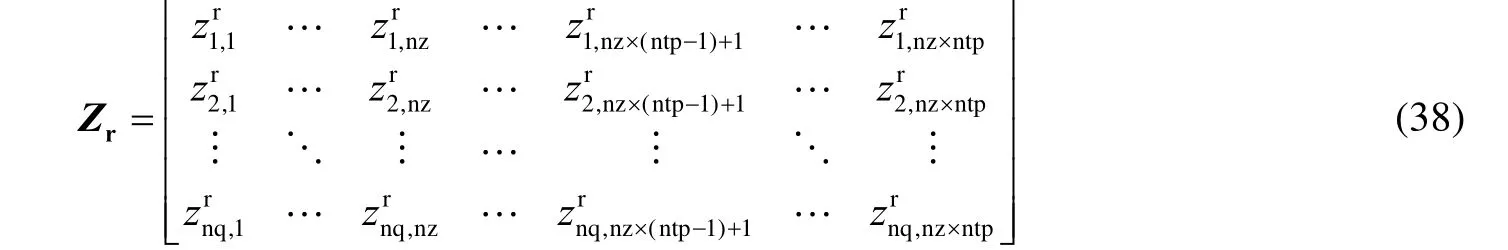
用二元变量b=[b1,b2,…,bntp]T来确定哪个采样时刻tl(l=1,2,…,ntp)从时间序列中被选择。因此，关于时间序列S的Hr可以定义为

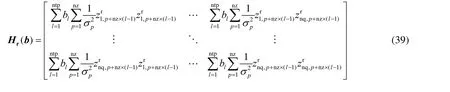
在当前参数θ下的协方差矩阵A=(Hr(b))-1，通过求解以下MINLP 问题来确定b，时间序列子集和合适的A矩阵元素am,s：

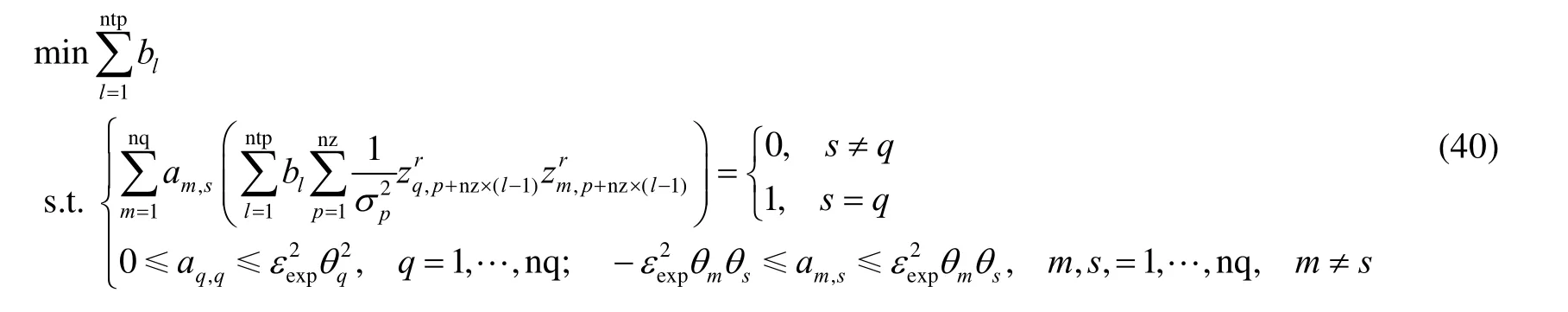
然而，使用问题式(40)的前提是，真实的估计参数值是先验已知的，但事实并非如此。相反，该策略通过在参数空间上进行随机采样来选择θ的候选值，并用每个候选值来解决问题(40)。从每个解中，记录从b中选择了哪些时间序列点，并观察从整个采样中选择时间序列点的频率，然后选择大频率的时间序列点进行参数估计。

并且Chen 等[20]证明了输出采样数量的增加会使得RSDEV 准则ε的值减小或者保持不变。因此，MINLP(40)的解决方案提供了一个最小的时间序列点集，并且同时保证了一个适当的比率ε。

3.3 拉丁超立方体采样

采样策略多次在参数空间中随机采样选择θ的候选值，并用每个候选值来解决问题式(40)，然而随机采样使结果充满不确定性。建立精确的代理模型要求采样点集可以描述模型在输入范围上的整体趋势变化，因而需要采样点足够均匀，数量也足够代表模型的变化，为了达到这一点，本研究采用了拉丁超立方体采样(Latin hypercube sampling，LHS)取代随机采样。LHS 是分层采样抽样技术中的一种，由Mckay等[27]于1979 年提出。分层抽样法将总体按一定特征或者规则划分为不同的层，然后从不同的层内进行独立、随机的抽样，相比于简单随机抽样，分层采样获得的样本代表性较好，抽样误差较小。

在LHS 方法中在每个维度上都进行了均匀的划分，但是采样点的数目不受限制。假设采样空间的维度为n，想要获得m个采样点，那么要将n个维度中的每个维度上的取值空间划分为m个等份，然后在每个维度的每个等分内都随机产生一个数值，由此就获得了n组数量为m的数值集合，之后将这n组数值集合内的点随机组合，就获得了所需要的m个采样点[28]。

在此策略中，维度由参数子集选择技术决定，设可估参数子集个数为nq，采样次数为nrs，将参数子集的参数空间分成nrs 个等份，在每个等份中随机取一个值，将nq 组数值集合内的点随机组合，获得输入采样。

3.4 算法步骤

步骤1：通过模型式(32)确定可估计参数子集，可估参数子集个数为nq。

步骤2：设定式(40)中的εexp，乘子η>1，采样次数为nrs。

步骤3：设定可估计参数的参数空间，用拉丁超立方体采样在参数空间里采样nrs 次生成候选参数，并解决nrs 次候选参数的问题式(40)，然后根据所有采样的参数值计算时间序列点的频率。

步骤4：设最终采样集合S由nq×η个时间序列点组成，选择频率最高的nq×η个时间点组成S。

步骤5：用集合S中的采样点时刻的测量值来求解问题(36)，即参数估计；计算参数协方差矩阵A，并表示最大比率δq/θq，q=1,…,nq。

步骤6：如果δq/θq<εexp，转至步骤9。

步骤7：如果δq/θq≥εexp，设Sl={1, 2,…, ntp}-S，对Sl中的每个元素{v}，令St=S+{v}，并计算其Hr和协方差矩阵A，并保留其δq*/θq*的值。

步骤8：选择δq*/θq*的最大值对应的元素vmax，令S=S+{vmax}，返回步骤5。

步骤9：结束。

算法流程图如图(1)所示：

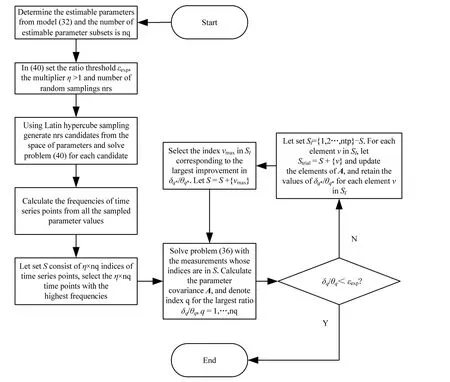
图1 最优策略算法流程图Fig.1 Flow chart of the optimal strategy algorithm

4 仿真实验

以质量分数的分布作为测量输出，通过加入方差1×10-4来模拟测量值，有限元个数为30 个，每个有限元配置点K=3，共有90 个潜在采样点。根据第3 节的参数子集选择方法，设定εexp=0.05，被估计参数子集θ=[kp(2),ktH(1),kaA(2)]，nq=3，其参数空间的范围分别为3 554.041≤kp(2)≤3 871.933，L·(mol·s)-1；182.361≤ktH(1)≤216.283，L0.5·mol-0.5·s-1；204.329≤kaA(2) ≤242.987，L·(mol·s)-1；设定式(40)中的εexp=0.05，乘子η=2，采样次数nrs 为100。在最优采样策略的步骤3 中，使用随机采样，得出所有时间点的频率，如图2 所示。

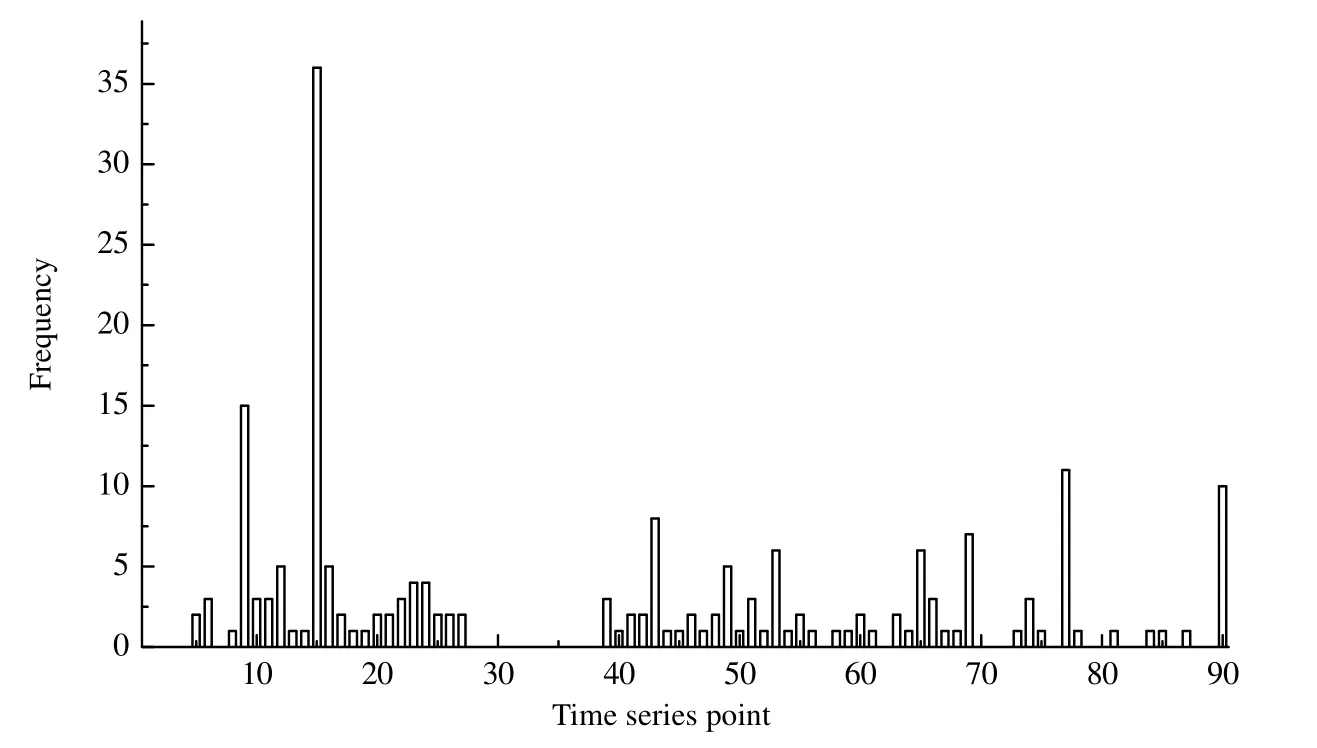
图2 采用随机采样策略得到的时间序列点选择频率Fig.2 Frequency of time series points for estimating the parameter range of HDPE using random sampling

根据频率最高选择采样时间点S={9, 15, 43, 69, 77, 90}，采样时间点数量为6。使用选择的采样时间点估计参数θ=[kp(2),ktH(1),kaA(2)]，其值分别为[3 423.207, 221.58, 244.6]，其δq/θq分别为[0.038 8, 0.045 5,0.048 4]，误差分别为6.23%、6.27%、7.23%。

用拉丁超立方体采样代替步骤3中的随机采样，同样得到所有采样的参数值计算时间序列点的频率，如图3所示。

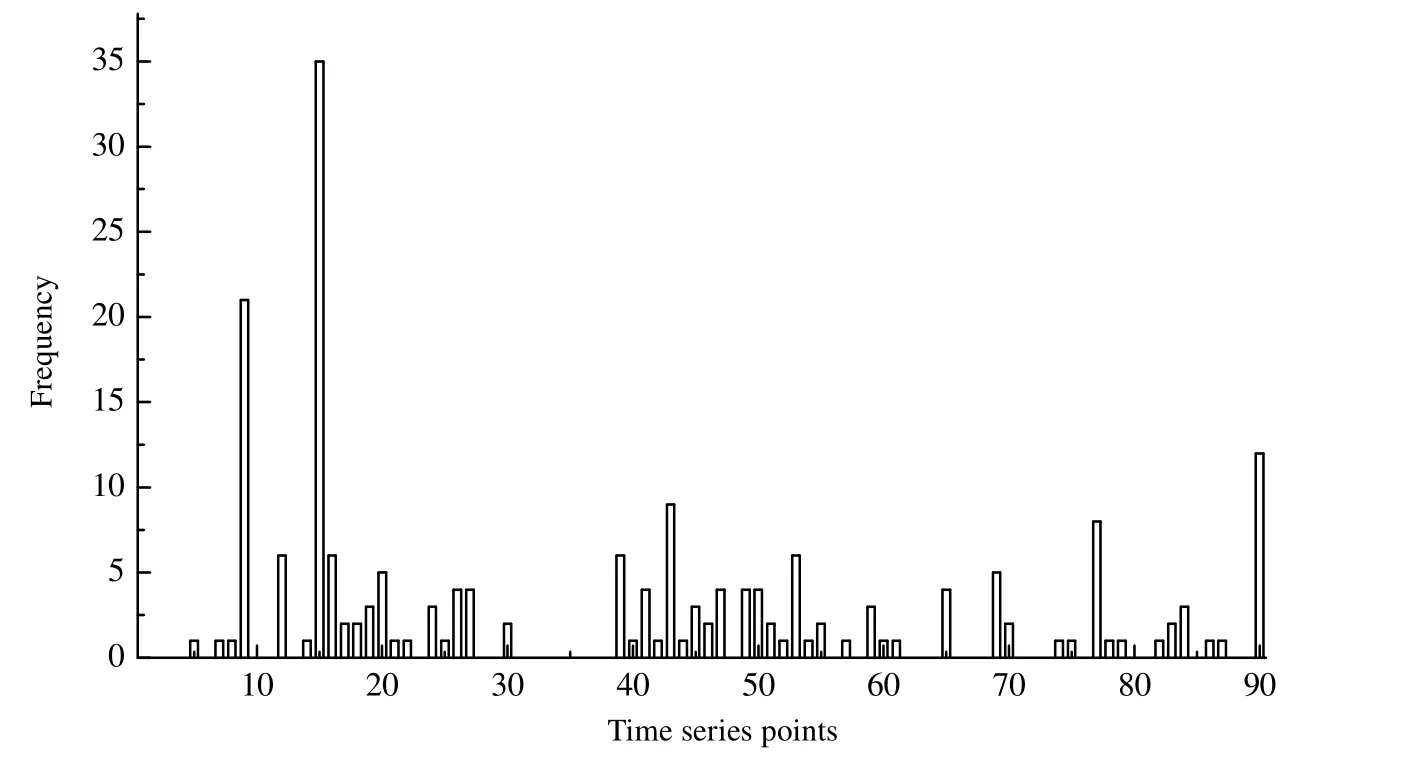
图3 采用拉丁超立方体采样策略得到的时间序列点选择频率Fig.3 Frequency of time series points for estimating the parameter range of HDPE using Latin hypercube sampling

根据频率最高选择采样时间点S={9, 12, 15, 43, 77, 90}，采样时间点数量为6。使用选择的采样时间点估计参数θ=[kp(2),ktH(1),kaA(2)]，其值分别为[3 542.722, 213.84, 237.2]，其δq/θq分别为[0.033 3, 0.036 9,0.040 5]，误差分别为2.96%、2.56%、3.97%。

为对比在步骤3中使用拉丁超立方体采样与使用随机采样对最终参数估计的影响，分别使用这2种采样方法仿真了10次，并且取其误差平均值作为对比。使用随机采样的参数估计的误差平均值为5.82%、6.12%、6.99%，其方差分别为0.000 325，0.000 436，0.000 387，使用拉丁超立方体采样的参数估计的误差平均值为3.63%、3.49%、4.11%，其方差分别为0.000 377、0.000 631、0.000 563。

5 结 语

针对HDPE 模型的样本分析成本过高且参数估计困难问题，提出使用简约Hessian 矩阵代替FIM 并结合RSDEV 准则作为新的参数子集选择方法，其优势在于避免了HDPE 模型灵敏度矩阵S计算成本过大和组合爆炸问题。此外，在保证参数估计精度的情况下，为了减少采样点个数，降低样本分析成本，提出一种基于拉丁超立方体采样的近似最优采样策略。通过拉丁超立方体采样获得参数空间候选值，并建立和求解最优采样子问题，构建了各潜在采样点的选择频率，使用一种启发式策略和迭代增强策略选择最终采样点，并实现了参数估计。为了验证采样策略结果的可靠性，使用了基于随机采样的最优采样策略进行对比。使用新的参数子集选择方法选出的待估参数为kp(2)、ktH(1)、kaA(2)，同时仿真结果表明，最终在90 个潜在采样点中仅采样其中6 个，大大减少了采样点个数，降低了样本分析成本，使用随机采样的参数估计相对误差平均值分别为5.82%、6.12%、6.99%，使用拉丁超立方体采样的参数估计的相对误差平均值分别为3.63%、3.49%、4.11%。从仿真结果可以看出参数估计精度在可接受范围，而且基于拉丁超立方体采样比基于随机采样的参数估计结果更加精确、稳定。此外，该最优采样策略还适用于不能在线测量和对样本离线分析成本很高的情况。