基于乘性扩展卡尔曼滤波的水下机器人姿态估计*
2022-11-11王子梦罗瑞智
唐 军, 王子梦, 罗瑞智
(江西理工大学 机电工程学院,江西 赣州 341000)
0 引 言
随着低成本惯性传感器的出现,特别是基于微机电系统(micro-electro-mechanical system,MEMS)的惯性传感器[1]的出现,姿态估计[2]技术的应用领域大大拓宽,广泛应用于航天器、机器人等领域。对于缆控水下机器人(remotely operated vehicle,ROV)[3]来说,实时精准的姿态信息是其控制和决策的基础。ROV航姿参考系统(attitude and heading reference system,AHRS)由陀螺仪、加速度计以及磁力计组合而成。其中,陀螺仪动态响应快,测量精度高,但存在积分漂移问题;加速度计虽然不会产生积分误差,但运行时数据噪声特别大;磁力计极其容易受到外界金属及电磁设备的干扰和影响。因此,使用姿态估计算法融合各传感器的测量数据,实现优势互补,具有重要的研究意义。
常见的姿态估计算法有三种:梯度下降(gradient descent,GD)法[4]、显性互补滤波(explicit complementary filtering,ECF)[5]以及卡尔曼滤波。扩展卡尔曼滤波(extended Kalman filtering,EKF)是目前最常用的非线性姿态估计算法。根据状态向量中使用的姿态表示形式不同以及观测量的形式不同,EKF的实现方式[6]有乘性扩展卡尔曼滤波(multiplicative EKF,MEKF)和加性扩展卡尔曼滤波(additive EKF,AEKF)。其中,MEKF[7]被视为姿态估计的标准算法,广泛应用于航空航天[8]、机器人[9]等领域,但在水下机器人领域的应用较少。
因此,本文以水下机器人CHASING M2 ROV为研究对象,用四元数表示ROV姿态角度,建立MEMS传感器测量模型,设计了基于MEKF的姿态估计算法。为验证其可行性,采集ROV水下动态实验数据进行融合,与AHRS获得的参考值相比较,并在仿真环境下,将其与ECF,GD两种算法分析对比。
1 四元数姿态表示
1.1 坐标系建立
机体坐标系obxbybzb与机体固连,如图1所示。通常以地心作为坐标原点oe,以北、东、地方向为大地坐标系的正方向。规定机体旋转的正方向为右手螺旋方向。机体绕obxb轴旋转的角度即滚转角φ(roll),绕obyb轴旋转的角度即俯仰角θ(pitch),绕obzb轴旋转的角度即偏航角ψ(yaw)。
选取的大地坐标系oexeyeze与机体坐标系obxbybzb的关系如图2所示。

图1 ROV机体坐标系

图2 机体坐标系与大地坐标系的关系
1.2 姿态表示


(1)
四元数一般表示为
(2)
式中q0∈为q∈4的标量部分,qv=[q1q2q3]T∈3为向量部分。
从机体坐标系到大地坐标系的旋转矩阵可以用四元数表示[10]为
(3)
最后,联立式(1)、式(3)可得出四元数与欧拉角之间的转换关系为
(4)
2 传感器测量模型
2.1 陀螺仪测量模型
MEMS陀螺仪固连于机体内,轴向与机体坐标系一致,测量的是三个机体轴方向的角速度。测量模型表示为
ω=ωm-ωb-ωn
(5)
式中ω∈3为角速度的真值;ωm∈3为角速度测量值;ωb∈3为漂移误差;ωn∈3为陀螺仪测量噪声向量,可以看成高斯白噪声向量。
2.2 加速度计测量模型
MEMS加速度计固连于机体内,其轴向与机体坐标系一致,测量的是三个机体轴向的比力分量。测量模型表示为
a=am-ab-an
(6)
式中a∈3为比力的真值;am∈3为加速度计测量值;ab∈3为漂移误差;an∈3为加速度计测量噪声向量,为高斯白噪声向量。
2.3 磁力计测量模型
记磁场矢量为em∈3。磁力计固连于机体内,其轴向于机体坐标系一致。它测量的是沿着不同方向轴的磁场矢量,记为bmm∈3。建立测量模型为
(7)
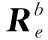
3 MEKF姿态估计
MEKF将真实状态分为标称状态和误差状态两部分。对两种状态分别进行估计,最后将结果进行叠加,以获取真实估计。其原理如图3所示。
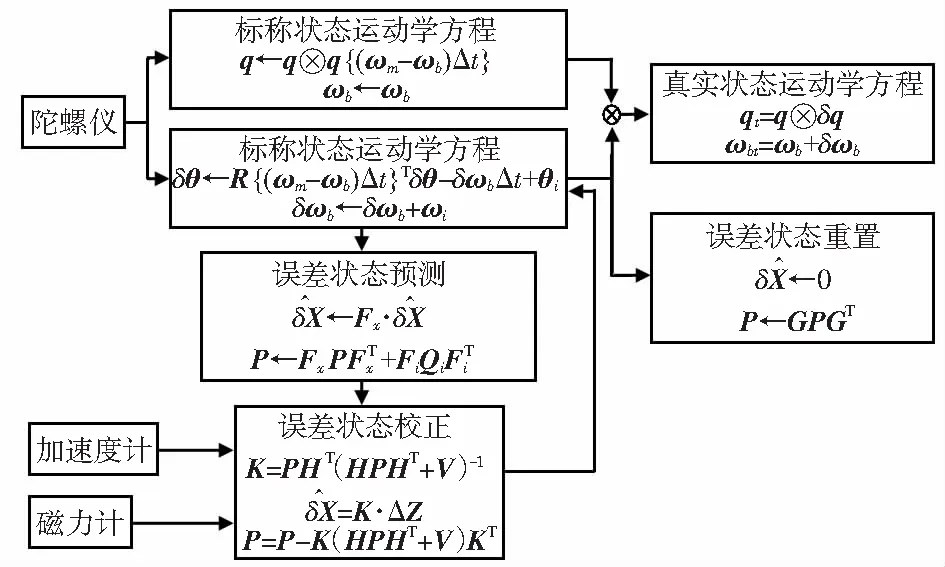
图3 MEKF算法原理框图
3.1 状态变量
定义真实状态变量Xt,标称状态变量X,误差状态变量δX为
(8)
式中q,δq,δθ分别为四元数、误差四元数以及误差旋转向量,ωb,δωb分别为陀螺仪偏差和偏差误差,qt为真实状态四元数,ωt为真实偏差。
3.2 标称状态方程模型
(9)
进一步离散化,得到递推表达式
(10)
3.3 误差状态方程模型
由误差状态连续时间运动学方程
(11)
离散化得到递推表达式
(12)
其中
(13)
式中θi,ωi为高斯随机脉冲噪声。式(13)为旋转向量转换为旋转矩阵的转换公式,即罗德里格旋转公式[7]。其中,[u]×为旋转向量的反对称矩阵。
3.4 误差状态预测
由式(8)建立误差状态预测方程
(14)
式中P为误差协方差矩阵;Fx和Fi为误差状态变量和噪声变量的雅可比矩阵;Qi为噪声变量的协方差矩阵
另外,相关的调查数据显示,中国物流并购标的企业所在地主要集中在东部地区,其中以发达地区、沿海省份为主。这些地区或城市凭借着经济优势或地域优势成为近10年物流并购的热点地区,而且这些地区并购发生量占全国总并购数目的68%。

(15)
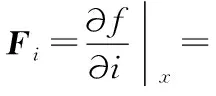
(16)
3.5 误差状态观测
以加速度计和磁力计作为观测信息,得到观测方程
(17)
分别对加速度计和磁力计观测方程求偏导,得到雅可比矩阵Hx
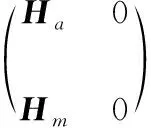
(18)
由链式求导法则,求得观测方程关于误差状态变量δX的雅可比矩阵H
(19)
式中XδX为真实状态关于误差状态的雅可比矩阵,Qδθ为真实状态四元数关于误差旋转矢量的雅可比矩阵
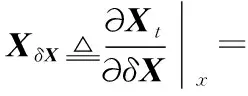
(20)
由式(17),结合传感器实际测量值可得观测信息ΔZ
ΔZ=Z-=
(21)
3.6 误差状态校正
对误差状态预测后,需要进行补偿修正。由式(14)、式(19)、式(21)可得校正方程
(22)
式中V为测量噪声方差阵。
3.7 误差状态与标称状态融合
误差状态更新后,将其与标称状态融合,标称状态也随之更新
(23)
根据式(4)、式(23)即可由实时更新的四元数转换得到姿态信息。
3.8 误差状态重置
误差状态融合进标称状态后,必须重置处理
(24)
式中G=I6×6,为6阶单位阵。
4 实验与仿真
为了验证所设计的MEKF算法的性能,将ROV放入水中进行动态实验,完成了滚转、俯仰、偏航等动作,获取传感器数据后,在MATLAB中分别实现ECF,GD,MEKF算法仿真。如图4所示。
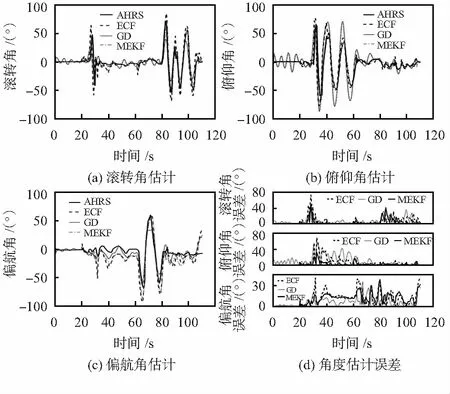
图4 ECF,GD,MEKF姿态估计及绝对误差
由图4(a)~(c)可以看出,三种算法均对AHRS参考值具有较好的逼近效果。其中,GD算法的收敛性能不足,估计数值在参考值附近振荡现象较为严重,而且动态性能较差。这是没有选取合适的迭代步长导致的。ECF算法有较强的收敛性和动态性,但存在准确性不足的问题。
经过统计分析图4(d)的数据,得到动态实验下各角度的绝对误差均值Mean与均方根误差(root mean square error,RMSE)对比结果,如表1所示。

表1 各算法在动态实验下姿态估计误差分析统计表
由表1可知,从滚转角来看,本文MEKF算法的误差均值分别较ECF,GD减少了39.14 %和42.10%,而RMSE略小于ECF,GD。从俯仰角来看,本文MEKF算法效果尤为明显,误差均值较ECF,GD分别减少了60.46 %和77.20 %,RMSE分别减少了61.14 %和65.58 %。从偏航角来看,本文MEKF算法效果略优于ECF。
5 结 论
针对ROV姿态估计问题,本文设计了基于MEKF的姿态估计算法。该算法将真实状态分为标称状态和误差状态,通过离散化状态运动学方程,得到状态递推表达式,采用扩展卡尔曼滤波框架估计误差状态,并与标称状态融合,得到真实状态。为验证其可行性,结合动态实验数据进行仿真。结果表明:该算法估计效果最接近参考值,且性能较优。对实际应用于ROV姿态估计系统中具有参考意义。
